【2019年高考理科数学三论冲刺三角函数 教案
文档属性
| 名称 | 【2019年高考理科数学三论冲刺三角函数 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 414.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-06 16:45:51 | ||
图片预览




文档简介
2019年高考理科数学三论冲刺 三角函数
教材版本 全国通用 课时说明(建议) 120分钟
知识点 三角函数诱导公式、性质和图像、三角函数图像变换、三角函数和角与差角与倍角公式公式,简单的三角恒等变换及辅助角公式
复习目标 了解正切函数图像,掌握三角函数基本概念及正弦余弦函数图像及性质,熟记三角函数和差角公式
复习重点 三角函数图像及平移变换、通过和差角求给定的三角函数值、灵活使用辅助教公式,求解相关的范围问题
复习难点 图像与性质,三角恒等变换的使用
一、高考回顾
纵观前几年高考试题, 三角函数的周期性、单调性、最值,三角函数图像变换等是高考的热点,每年文理均涉及到一道三角函数性质与图像的题目,题型既有选择题、填空题,又有解答题,难度属于中、低档;常与三角恒等变换交汇命题,在考查三角函数性质的同时,又考查三角恒等变换的方法与技巧,注重考查函数与方程、转化与化归等思想方法.
二、知识清单
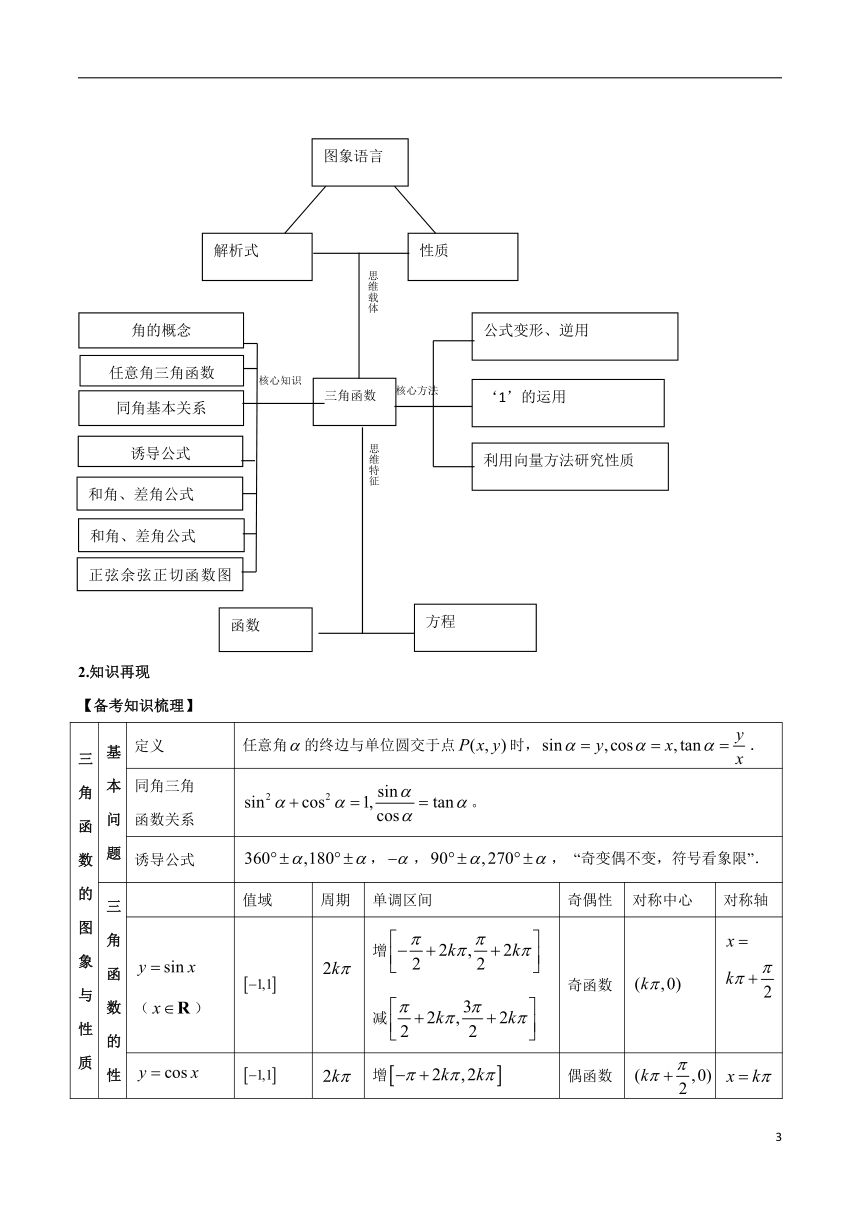
1.思维导图
建议仿照下面的思维导图形式来呈现本部分的核心知识、核心方法、思维特征、思维载体等内容。
2.知识再现
【备考知识梳理】
三角函数的图象与性质 基本问题 定义 任意角的终边与单位圆交于点时,.
同角三角 函数关系 。
诱导公式 ,,, “奇变偶不变,符号看象限”.
三角函数的性质与图象 值域 周期 单调区间 奇偶性 对称中心 对称轴
() 增 减 奇函数
() 增 减 偶函数
() 增 奇函数 无
图象变换 平移变换 上下平移 图象平移得图象,向上,向下。
左右平移 图象平移得图象,向左,向右。
伸缩变换 轴方向 图象各点把横坐标变为原来倍得的图象。
轴方向 图象各点纵坐标变为原来的倍得的图象。
对称变换 中心对称 图象关于点对称图象的解析式是
轴对称 图象关于直线对称图象的解析式是。
三角恒等变换 变换公式 正弦 和差角公式 倍角公式
余弦
正切
辅助角公式
三、例题精讲
题型一 三角函数的概念、诱导公式及同角关系式
例1 (1)点P从(1,0)出发,沿单位圆x2+y2=1逆时针方向运动弧长到达Q点,则Q点的坐标为( )
A.(-,) B.(-,-)
C.(-,-) D.(-,)
(2)已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边上一点P(-4,3),则的值为________.
【答案】(1)A(2)-
【解析】(1)设Q点的坐标为(x,y),
则x=cos=-,y=sin=.
∴Q点的坐标为(-,).
(2)原式==tan α.
根据三角函数的定义,
得tan α==-,
∴原式=-.
【易错点】诱导公式和三角函数定义不熟练
【思维点拨】(1)涉及与圆及角有关的函数建模问题(如钟表、摩天轮、水车等),常常借助三角函数的定义求解.应用定义时,注意三角函数值仅与终边位置有关,与终边上点的位置无关.
(2)应用诱导公式时要弄清三角函数在各个象限内的符号;利用同角三角函数的关系化简过程要遵循一定的原则,如切化弦、化异为同、化高为低、化繁为简等.
题型二 三角函数的图象及应用
例1【2017全国卷Ⅰ,理9】已知曲线,,则下面结正确的是( ).
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
【答案】D
【解析】(1) ,,首先曲线、统一为一三角函数名,可将用诱导公式处理..横坐标变换需将变成,即.
注意的系数,在右平移需将提到括号外面,这时平移至,根据“左加右减”原则,“”到“”需加上,即再向左平移.故选D.
【易错点】函数图像水平方向平移容易出错
【思维点拨】平移变换理论
(1)平移变换:
①沿x轴平移,按“左加右减”法则;
②沿y轴平移,按“上加下减”法则.
(2)伸缩变换:
①沿x轴伸缩时,横坐标x伸长(0<ω<1)或缩短(ω>1)为原来的 倍(纵坐标y不变);
②沿y轴伸缩时,纵坐标y伸长(A>1)或缩短(0
例2函数的部分图像大致为( ).
【答案】C
【解析】由题意知,函数为奇函数,故排除B;当时,,排除D;当时,,排除A.故选C.
【易错点】函数图形判断通过过排除法
【思维点拨】
例3函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是( )
A.2,- B.2,-
C.4,- D.4,
【答案】A
【解析】 (1)因为=-,所以T=π.又T=(ω>0),所以=π,所以ω=2.
又2×+φ=+2kπ(k∈Z),且-<φ<,故φ=-.
【易错点】求φ时,容易忽略讨论k
【思维点拨】
题型三 三角函数性质
例1 (1)已知函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,0<|φ|<)为奇函数,且函数y=f(x)的图象的两相邻对称轴之间的距离为.
(1)求f()的值;
(2)将函数y=f(x)的图象向右平移个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递增区间.
【答案】(1)f()=2sin=(2)[kπ-,kπ+](k∈Z).
【解析】(1)f(x)=sin(ωx+φ)+cos(ωx+φ)
=2[sin(ωx+φ)+cos(ωx+φ)]
=2sin(ωx+φ+).
因为f(x)为奇函数,所以f(0)=2sin(φ+)=0,
又0<|φ|<,
可得φ=-,
所以f(x)=2sin ωx,由题意得=2·,所以ω=2.
故f(x)=2sin 2x.
因此f()=2sin=.
(2)将f(x)的图象向右平移个单位后,得到f(x-)的图象,
所以g(x)=f(x-)=2sin[2(x-)]=2sin(2x-).
当2kπ-≤2x-≤2kπ+(k∈Z),
即kπ-≤x≤kπ+(k∈Z)时,
g(x)单调递增,
因此g(x)的单调递增区间为[kπ-,kπ+](k∈Z).
【易错点】
【思维点拨】
题型四三角函数范围问题
例1函数的最大值是 .
【答案】1
【解析】,
令且,,
则当时,取最大值1.
【易错点】换元之后转化为二次函数在定区间上的定义域及最值
【思维点拨】
例2函数的最大值为 .
【答案】
【解析】.
【易错点】
【思维点拨】辅助角公式运用
例3【2017年Ⅲ】函数的最大值为( ).
A. B.1 C. D.
【答案】A
【解析】
.故选A.
【易错点】本题属于中档题,基础差一点的学生在解题思路方面可能会存在一定问题,三角恒等变换中公式的选择对于学生来说是一个难点,对于老师教学来说是一个重点,选择合适的公式能起到事半功倍的效果!
【思维点拨】
题型五三角函数求值问题
例1已知,,则 .
【答案】
【解析】由 又,
所以 .因为,所以,.
因为,
所以.
【易错点】
【思维点拨】
例2(1)若,则( )
(A) (B) (C) 1 (D)
(2)( )
A. B. C. D.
【答案】(1)A(2)
【解析】(1)由,,得,或,
,所以,则,故选A
(2)原式=
【易错点】
【思维点拨】
例3已知函数f(x)=sinsin x-cos2x.
(1)求f(x)的最小正周期和最大值;
(2)讨论f(x)在上的单调性.
【答案】(1)f(x)的最小正周期为π,最大值为,(2)f(x)在上单调递增;在上单调递减
【解析】 (1)f(x)=sinsin x-cos2x
=cos xsin x-(1+cos 2x)=sin 2x-cos 2x-=sin-,
因此f(x)的最小正周期为π,最大值为.
(2)当x∈时,0≤2x-≤π,从而当0≤2x-≤,即≤x≤时,
f(x)单调递增,
当≤2x-≤π,即≤x≤时,
f(x)单调递减.
综上可知,f(x)在上单调递增;在上单调递减.
【易错点】
【思维点拨】解答技巧,方法策略等
题型六 简单的三角恒等变换
例1(2018·新疆第二次适应性检测)的值是________.
【答案】2
【解析】依题意得====2.
【易错点】
【思维点拨】解答技巧,方法策略等
例2已知tan α=2.
(1)求tan的值;
(2)求的值.
【答案】(1)-3(2)1
【解析】(1)tan===-3.
(2)
=
===1.
【易错点】
【思维点拨】
解三角函数的给值求值问题的基本步骤
(1)先化简所求式子或所给条件;
(2)观察已知条件与所求式子之间的联系;
(3)将已知条件代入所求式子,化简求值.
例3若sin 2α=,sin(β-α)=,且α∈,β∈,则α+β的值是( )
A. B.
C.或 D.或
【答案】A
【解析】选A ∵α∈,∴2α∈,∵sin 2α=,∴2α∈.
∴α∈且cos 2α=-,又∵sin(β-α)=,β∈,∴β-α∈,cos(β-α)=-,
∴cos(α+β)=cos[(β-α)+2α]=cos(β-α)cos 2α-sin(β-α)sin 2α=×-×=,
又α+β∈,所以α+β=.
【易错点】
【思维点拨】
对于给值求角问题,通过先求角的某个三角函数值来求角,在选取函数时,遵循以下原则:
(1)已知正切函数值,选正切函数.
(2)已知正、余弦函数值,选正弦或余弦函数.
若角的范围是,选正弦或余弦函数皆可;若角的范围是(0,π),选余弦函数较好;若角的范围为,选正弦函数较好.
四、成果巩固
题型一 三角函数的概念、诱导公式及同角关系式
1. 已知角的顶点为坐标原点,始边为轴的正半轴,若是角终边上一点,且,则 .
【答案】-8.
【解析】由tan==,得tanθ=,∴sinθcosθ====.故填.
2. (1)已知tan α=2,求值:
①;②4sin2α-3sin αcos α-5cos2α.
(2)已知θ∈(0,π),且sin θ+cos θ=,求sin θ-cos θ的值.
【答案】(1)①-1②1(2)
【解析】(1)①===-1.
②4sin2α-3sin αcos α-5cos 2α
==
==1.
(2)∵sin θ+cos θ=,∴(sin θ+cos θ)2=1+2sin θcos θ=,
∴sin θcos θ=-.∵θ∈(0,π),θ∈,
∴sin θ>0>cos θ,sin θ-cos θ>0.
由(sin θ-cos θ)2=1-2sin θcos θ=1+=,得sin θ-cos θ=.
3.若cos(π-α)=且α∈,则sin(π+α)=( )
A.- B.-
C.- D.±
【答案】B
【解析】cos (π-α)=-cos α=,∴cos α=-.
又∵α∈,∴sin α===,
∴sin (π+α)=-sin α=-,故选B.
题型二 三角函数图像
1. (2018·浙江温州模拟)为了得到函数y=sin 3x+cos 3x的图象,可以将函数y=cos 3x的图象( A )
A.向右平移个单位 B.向右平移个单位
C.向左平移 个单位 D.向左平移个单位
【答案】A
【解析】因为y=sin 3x+cos 3x=cos,所以将y=cos 3x的图象向右平移个单位后可得到y=cos的图象.
2.函数f(x)=Asin(ωx+φ)的部分图象如图所示,若x1,x2∈,且f(x1)=f(x2),则f(x1+x2)=( )
A.1 B.
C. D.
【答案】D
【解析】 观察图象可知,A=1,T=π,∴ω=2,f(x)=sin(2x+φ).
将代入上式得sin=0.
由|φ|<,得φ=,则f(x)=sin.
函数图象的对称轴为x==.
又x1,x2∈,且f(x1)=f(x2),∴=,
∴x1+x2=,∴f(x1+x2)=sin=,故选D.
3.已知函数f(x)=2sin(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间上的单调性.
【答案】(1) ω=1(2) f(x)在区间上单调递增,
在区间上单调递减.
【解析】 (1)因为f(x)=2sin的最小正周期为π,且ω>0.从而有=π,故ω=1.
(2)因为f(x)=2sin.
若0≤x≤,则≤2x+≤.
当≤2x+≤,即0≤x≤时,f(x)单调递增;
当<2x+≤,即
在区间上单调递减.
题型三 三角函数性质
1. 已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是( )
A. B.
C. D.[0,2]
【答案】A
【解析】由
解得≤ω≤,故选A.
2. (2017·全国卷Ⅲ)设函数f(x)=cos,则下列结论错误的是( )
A.f(x)的一个周期为-2π
B.y=f(x)的图象关于直线x=对称
C.f(x+π)的一个零点为x=
D.f(x)在单调递减
【答案】D
【解析】根据函数解析式可知函数f(x)的最小正周期为2π,所以函数一个周期为-2π,A项正确;当x=时,x+=3π,所以cos=-1,所以B项正确;f(x+π)=cos =cos,当x=时,x+=,所以f(x+π)=0,所以C项正确;函数f(x)=cos在上单调递减,在上单调递增,故D项不正确,故选D.
3. (2017·湖南岳阳一中月考)已知函数①y=sin x+cos x,②y=2sin xcos x,则下列结论正确的是( )
A.两个函数的图象均关于点中心对称
B.两个函数的图象均关于直线x=-对称
C.两个函数在区间上都是单调递增函数
D.将函数②的图象向左平移个单位得到函数①的图象
【答案】C
【解析】函数①y=sin x+cos x=sin,②y=2·sin xcos x=sin 2x,由于①的图象关于点中心对称,②的图象不关于点中心对称,故A项不正确;由于函数①的图象不可能关于直线x=-对称,故B项不正确;由于这两个函数在区间上都是单调递增函数,故C项正确;将函数②的图象向左平移个单位得到函数y=sin的图象,而y=sin≠sin,故D项不正确,故选C.
题型四三角函数范围问题
1.(2018全国Ⅰ,理16)已知函数f(x)=2sin x+sin 2x,则f(x)的最小值是 .?
【答案】
【解析】由题意可得T=2π是f(x)=2sin x+sin 2x的一个周期,所以求f(x)的最小值可考虑求f(x)在[0,2π)上的值域.
由f(x)=2sin x+sin 2x,得f'(x)=2cos x+2cos 2x=4cos2x+2cos x-2.令f'(x)=0,可得cos x=或cos x=-1,x∈[0,2π)时,解得x=或x=或x=π.因为f(x)=2sin x+sin 2x的最值只能在x=,x=,x=π或x=0时取到,且f,f=-,f(π)=0,f(0)=0,所以函数f(x)的最小值为-
2.已知y=3-sin x-2cos2x,x∈,求y的最大值与最小值之和.
【答案】
【解析】 ∵x∈,∴sin x∈.
又y=3-sin x-2cos2x=3-sin x-2(1-sin2x)
=22+,
∴当sin x=时,ymin=;
当sin x=-或sin x=1时,ymax=2.
故函数的最大值与最小值的和为2+=.
3.已知函数f(x)=sin(ωx+φ)(0<ω<1,0≤φ≤π)是R上的偶函数,其图象关于点M对称.
(1)求ω,φ的值;
(2)求f(x)的单调递增区间;
(3)若x∈,求f(x)的最大值与最小值,
【答案】(1)ω=.(2) ,k∈Z(3) 函数f(x)的最大值为1,最小值为0.
【解析】(1)因为f(x)=sin(ωx+φ)是R上的偶函数,所以φ=+kπ,k∈Z,且0≤φ≤π,则φ=,即f(x)=cos ωx.
因为图象关于点M对称,
所以ω×π=+mπ,m∈Z,ω=+,
又0<ω<1,所以ω=.
(2)由(1)得f(x)=cos x,由-π+2kπ≤x≤2kπ,且 k∈Z得,3kπ-≤x≤3kπ,k∈Z,
所以函数的递增区间是,k∈Z.
(3)因为x∈,所以x∈,
当x=0时,即x=0,函数f(x)的最大值为1,
当x=-时,即x=-,函数f(x)的最小值为0.
题型五三角函数求值问题
1.设α,β为钝角,且sin α=,cos β=-,则α+β的值为( )
A. B.
C. D.或
【答案】 C
【解析】∵α,β为钝角,sin α=,cos β=-,∴cos α=,sin β=,
∴cos(α+β)=cos αcos β-sin αsin β=>0.
又α+β∈(π,2π),∴α+β∈,∴α+β=.
2.已知函数f(x)=2cos2ωx-1+2sin ωxcos ωx(0<ω<1),直线x=是函数f(x)的图象的一条对称轴.
(1)求函数f(x)的单调递增区间;
(2)已知函数y=g(x)的图象是由y=f(x)的图象上各点的横坐标伸长到原来的2倍,然后再向左平移个单位长度得到的,若g=,α∈,求sin α的值.
【答案】(1)f(x)的单调递增区间为(k∈Z)(2)
【解析】 (1)f(x)=cos 2ωx+sin 2ωx=2sin,(2)
由于直线x=是函数f(x)=2sin的图象的一条对称轴,所以sin=±1,因此ω+=kπ+(k∈Z),
解得ω=k+(k∈Z),又0<ω<1,所以ω=,
所以f(x)=2sin.由2kπ-≤x+≤2kπ+(k∈Z),得2kπ-≤x≤2kπ+(k∈Z),
所以函数f(x)的单调递增区间为(k∈Z).
(2)由题意可得g(x)=2sin,即g(x)=2cos ,
由g=2cos=2cos=,得cos=,
又α∈,故<α+<,所以sin=,
所以sin α=sin=sincos -cossin =×-×=.
3.已知cos=,求cos-sin2的值.
【答案】-
【解析】 cos-sin2
=cos-sin2
=-cos-
=--=-.
题型六 简单的三角恒等变换
1.已知sin=cos,则cos 2α=( )
A.1 B.-1
C. D.0
【答案】选D
【解析】 ∵sin=cos,
∴cos α-sin α=cos α-sin α,即sin α=-cos α,
∴tan α==-1,∴cos 2α=cos2α-sin2α===0.
2.计算 =________(用数字作答).
【答案】
【解析】====.
3.已知cos α=,cos(α-β)=,且0<β<α<,则β=________.
【答案】
【解析】由cos α=,0<α<,
得sin α== =,
由0<β<α<,得0<α-β<,又∵cos(α-β)=,
∴sin(α-β)== =.
由β=α-(α-β),得cos β=cos[α-(α-β)]
=cos αcos(α-β)+sin αsin(α-β)
=×+×=.
∴β=.
五、课堂小结
1.求三角函数的周期、单调区间及判断其奇偶性的问题,常通过三角恒等变换将三角函数化为只含一个函数名称且角度唯一、最高次数为一次的形式.
2.由函数y=sin x的图象变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象有两种方法,一是先平移再伸缩,二是先伸缩再平移,要弄清楚是平移哪个函数的图象,得到哪个函数的图象;平移前后两个函数的名称是否一致,若不一致,应先利用诱导公式化为同名函数;当由y=Asin ωx的图象得到y=Asin(ωx+φ)(ω>0)的图象时,需平移的单位数应为,而不是|φ|.
3.函数y=Asin(ωx+φ)(ω>0)的性质主要有:(1)奇偶性,当φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;当φ=kπ+(k∈Z)时,函数y=Asin(ωx+φ)为偶函数;(2)周期性,y=Asin(ωx+φ)的最小正周期为T=;(3)单调性,由-+2kπ≤ωx+φ≤+2kπ(k∈Z)得单调递增区间,由+2kπ≤ωx+φ≤+2kπ(k∈Z)得单调递减区间;(4)对称性,令ωx+φ=kπ(k∈Z),求得对称中心,令ωx+φ=kπ+(k∈Z),求得对称轴.
4.对于函数y=Asin(ωx+φ),其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线x=x0或点(x0,0)是否是函数的对称轴或对称中心时,可通过检验f(x0)的值进行判断.
三角函数恒等变换
1.三角恒等变形的基本思路:
(1)“化异名为同名”“化异次为同次”“化异角为同角”;
(2)“切化弦”“1”的代换;
(3)角的变换是三角变换的核心,如β=(α+β)-α,2α=(α+β)+(α-β)等.
2.倍角、半角公式应用的技巧:公式的正用、逆用和变形用.
3.在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.正弦定理的形式多样,其中a=2Rsin A,b=2Rsin B,c=2Rsin C能够实现边角互化.
4.在解三角形中,三角形内角和定理起着重要作用,在解题中要注意根据这个定理确定角的范围,确定三角函数值的符号,防止出现增解等扩大范围的现象.
4
1
同课章节目录
