2019年高考理科数学三论冲刺数列 教案
文档属性
| 名称 | 2019年高考理科数学三论冲刺数列 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 780.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-06 16:47:03 | ||
图片预览

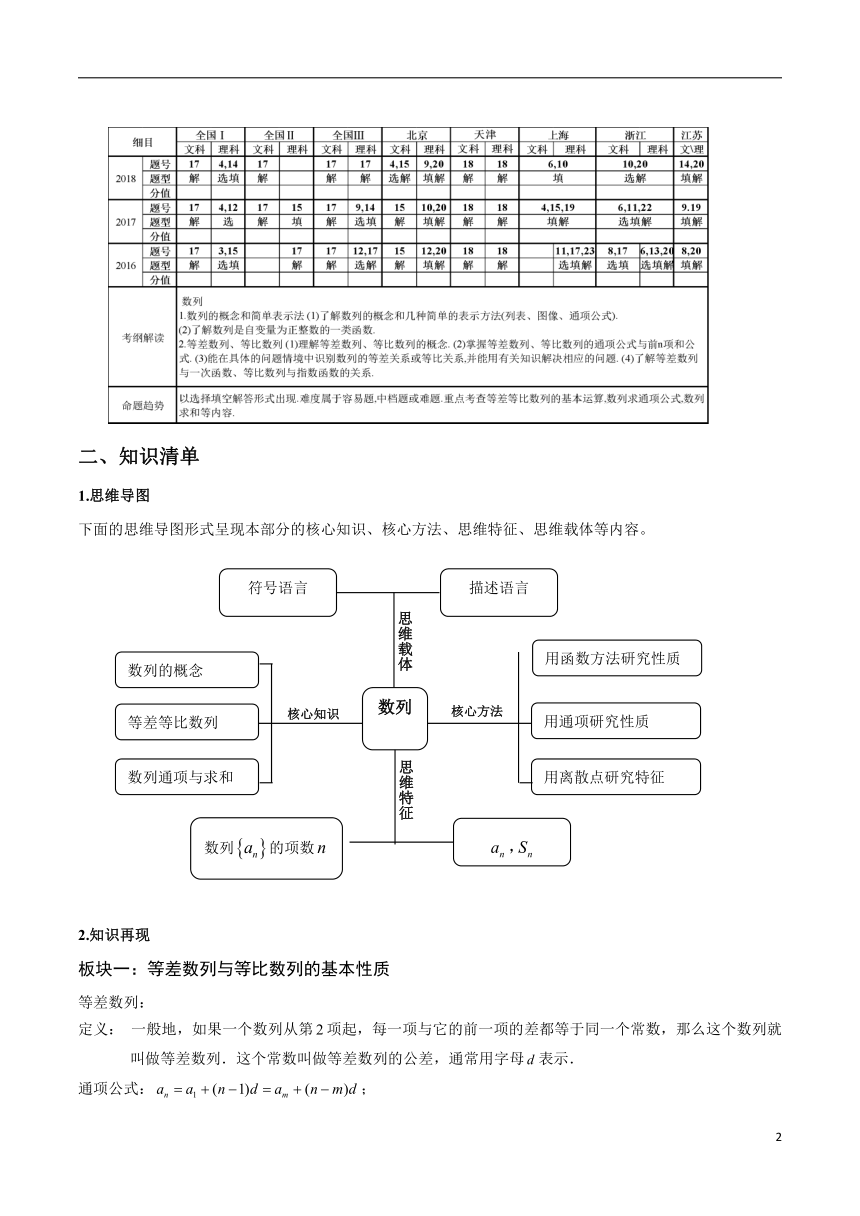



文档简介
2019年高考理科数学三轮冲刺数列
教材版本 全国通用 课时说明(建议) 120分钟
知识点 数列的概念和表示法,等差、等比数列的概念、性质、前n项和公式; 数列求和的常用方法,数列的通项公式
复习目标 ⑴数列的概念和简单表示法 ①了解数列的概念和几种简单的表示方法(列表、图象、通项公式). ②了解数列是自变量为正整数的一类函数. ⑵等差数列、等比数列 ①理解等差数列、等比数列的概念. ②掌握等差数列、等比数列的通项公式与前项和公式. ③能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题. ④了解等差数列与一次函数、等比数列与指数函数的关系. ⑶掌握数列求和方法.
复习重点 ⑴数列的概念和简单表示法 ⑵等差数列、等比数列 ⑶数列求和方法.
复习难点 ⑴数列的概念和简单表示法 ⑵等差数列、等比数列 ⑶数列求和方法.
一、高考回顾
统计了全国I卷近五年、全国II卷近五年、全国III卷近三年文理共26份试卷.以大题形式考查,全部是在第17题,14年II卷题考查了先放缩再求和,从而证明不等式,有一定难度,其它题均是基本题型,比较容易;以小题形式考查,有1题次出现在第12题(2017理科1卷,考查分组数列求和),2题次出现在题(递推公式求通项,),其它题都是偏容易题型,以数列基本量的换算题型出现次数最多.
重视转化与化归思想,无论是递推公式求通项,还是数列求和,都注重将一般数列转化为等差、等比数列解决;重视函数与方程思想,考查数列的函数特性,利用函数图像、性质等求数列的最大(小)项,数列基本量的换算体现的是设未知数、列方程、解方程的基本思想.
二、知识清单
1.思维导图
下面的思维导图形式呈现本部分的核心知识、核心方法、思维特征、思维载体等内容。
(
用函数方法研究性质
思维载体
数列
数列的概念
等差等比数列
数列通项与求和
核心知识
核心方法
思维特征
符号语言
描述语言
数列
的项数
用离散点研究特征
用通项研究性质
)
2.知识再现
板块一:等差数列与等比数列的基本性质
等差数列:
定义: 一般地,如果一个数列从第项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.这个常数叫做等差数列的公差,通常用字母表示.
通项公式:;
前项和公式:.
等差数列的性质(其中公差为):
⑴,;
⑵若,则有;若,则有(,,,);
⑶在等差数列中,等距离取出若干项也构成一个等差数列,即,,,为等差数列,公差为;
⑷等差数列的项和也构成一个等差数列,即,为等差数列,公差为;
⑸若等差数列的项数为,则有,;若等差数列的项数为奇数,则,且中间项,;
⑹为等差数列,为前项和,则;为等差数列,为前项和,;有.
等比数列:
定义:一般地,如果一个数列从第项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,通常用字母表示.等比数列中的项不为.
通项公式:;前项和公式:.
等比数列的性质(其中公比为):
⑴,;
⑵若,则有;若,则有;
⑶等距离取出若干项也构成一个等比数列,即,,,为等比数列,公比为.
⑷等比数列(公比不为-1)的项和也构成一个等比数列,即,为等比数列,公比为.
板块二:数列的通项公式
常见的已知递推式求通项公式的常用方法:
⑴(其中),则;
⑵(其中),则;
⑶(其中,,是关于的多项式函数),
可设,其中为与的次数相等的多项式函数,各项的系数都待定,通过比较与的各项系数可以确定待定系数;
⑷,其中,,,,.
若,则;
若,则可以设;也可两边同时除以:;
也可两边同时除以:.
板块三:特殊数列求和
1.直接法:即直接用等差、等比数列的求和公式求和.
(1)等差数列的求和公式:
(2)等比数列的求和公式(切记:公比含字母时一定要讨论)
2.公式法:
3.错位相减法:比如
4.裂项相消法:把数列的通项拆成两项之差、正负相消剩下首尾若干项.
常见拆项公式: ;
5.分组求和法:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和.
6.合并求和法:如求的和.
7.倒序相加法:如(C为常数).
8.其它求和法:如归纳猜想法,奇偶法等
三、例题精讲
考点1 等差数列、等比数列的基本运算
题组一 等差数列基本量的计算
例1 设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sn+2?Sn=36,则n=
A.5 B.6
C.7 D.8
【答案】D
【解析】解法一:由题知,Sn+2=(n+2)2,由Sn+2?Sn=36得,(n+2)2?n2=4n+4=36,所以n=8.
解法二:Sn+2?Sn=an+1+an+2=2a1+(2n+1)d=2+2(2n+1)=36,解得n=8.所以选D.
【易错点】对Sn+2?Sn=36,解析为an+2,发生错误。
题组二 等比数列基本量的计算
例2 在各项均为正数的等比数列{an}中,若,则a6的值是________.
【答案】4
【解析】设公比为q(q≠0),∵a2=1,则由得,即,解得q2=2,
∴.
【易错点】忘了条件中的正数的等比数列.
【思维点拨】
等差(比)数列基本量的计算是解决等差(比)数列题型时的基础方法,在高考中常有所体现,多以选择题或填空题的形式呈现,有时也会出现在解答题的第一问中,属基础题.等差(比)数列基本运算的解题思路:
(1)设基本量a1和公差d(公比q).
(2)列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
考点2等差数列、等比数列的判定与证明
题组一 等差数列的判定与证明
例1设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是a和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=?n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
【答案】(1)见解析;(2) 当n=2或n=3时,{an·bn}的最大项的值为6.
【解析】(1)由已知可得2Sn=a+an,且an>0,
当n=1时,2a1=a+a1,解得a1=1;
当n≥2时,有2Sn?1=a+an?1,
所以2an=2Sn?2Sn?1=a?a+an?an?1,
所以a?a=an+an?1,即(an+an?1)(an?an?1)=an+an?1,
因为an+an?1>0,
所以an?an?1=1(n≥2).
故数列{an}是首项为1,公差为1的等差数列.
(2)由(1)可知an=n,
设cn=an·bn,则cn=n(?n+5)=?n2+5n=?2+,
因为n∈N*,
所以当n=2或n=3时,{an·bn}的最大项的值为6.
【易错点】Sn是a和an的等差中项,无法构建一个等式去求解出an。
【思维点拨】
等差数列的判定与证明的方法:
定义法:或是等差数列;
定义变形法:验证是否满足;
等差中项法:为等差数列;
通项公式法:通项公式形如为常数为等差数列;
前n项和公式法:为常数为等差数列.
注意:
(1)若判断一个数列不是等差数列,只需找出三项,使得即可;
(2)如果要证明一个数列是等差数列,则必须用定义法或等差中项法.
题组二 等比数列的判定与证明
例2设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2.
(1)设bn=an+1?2an,证明:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
【答案】(1)见解析;(2) an=(3n?1)·2n?2.
【解析】(1)由a1=1及Sn+1=4an+2,得a1+a2=S2=4a1+2.
∴a2=5,
∴b1=a2?2a1=3.
又
①?②,得an+1=4an?4an?1,
∴an+1?2an=2(an?2an?1).
∵bn=an+1?2an,
∴bn=2bn?1,
故{bn}是首项b1=3,公比为2的等比数列.
(2)由(1)知bn=an+1?2an=3·2n?1,
∴?=,
故是首项为,公差为的等差数列.
∴=+(n?1)·=,
故an=(3n?1)·2n?2.
【易错点】对于bn=an+1?2an,在条件中无法构造出来,等比数列的判定与证明常用的方法不清楚.
【思维点拨】
等比数列的判定与证明常用的方法:
(1)定义法:为常数且数列是等比数列.
(2)等比中项法:数列是等比数列.
(3)通项公式法:数列是等比数列.
(4)前项和公式法:若数列的前项和,则该数列是等比数列.
其中前两种方法是证明等比数列的常用方法,而后两种方法一般用于选择题、填空题中.
注意:
(1)若要判定一个数列不是等比数列,则只需判定存在连续三项不成等比数列即可.
(2)只满足的数列未必是等比数列,要使其成为等比数列还需要.
考点3等差数列、等比数列的性质
题组一 等差数列性质的应用
例1若{an}是等差数列,首项a1>0,a2 016+a2 017>0,a2 016·a2 017<0,则使前n项和Sn>0成立的最大正整数n是
A.2 016 B.2 017
C.4 032 D.4 033
【答案】C
【解析】因为a1>0,a2 016+a2 017>0,a2 016·a2 017<0,所以d<0,a2 016>0,a2 017<0,
所以,,所以使前n项和Sn>0成立的最大正整数n是4 032.
【易错点】等差数列的求和与等差数列的某一项有关系。
题组二 等比数列性质的应用
例2已知数列{an}是等比数列,Sn为其前n项和,若a1+a2+a3=4,a4+a5+a6=8,则S12=
A.40 B.60
C.32 D.50
【答案】B
【解析】由等比数列的性质可知,数列S3,S6?S3,S9?S6,S12?S9是等比数列,即数列4,8,S9?S6,S12?S9是等比数列,因此S12=4+8+16+32=60,选B.
【易错点】,等式不会转化.
【思维点拨】
等差(比)数列的性质是每年高考的热点之一,利用等差(比)数列的性质进行求解可使题目减少运算量,题型以选择题或填空题为主,难度不大,属中低档题.
应用等差数列性质的注意点:
(1)熟练掌握等差数列性质的实质
等差数列的性质是等差数列的定义、通项公式以及前n项和公式等基础知识的推广与变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决许多等差数列问题.
(2)应用等差数列的性质解答问题的关键
寻找项数之间的关系,但要注意性质运用的条件,如若,则
,需要当序号之和相等、项数相同时才成立,再比如只有当等差数列{an}的前n项和Sn中的n为奇数时,才有Sn=na中成立.
应用等比数列性质时的注意点:
(1)在解决等比数列的有关问题时,要注意挖掘隐含条件,利用性质,特别是性质“若m+n=p+q,则am·an=ap·aq”,可以减少运算量,提高解题速度.
(2)在应用相应性质解题时,要注意性质成立的前提条件,有时需要进行适当变形.此外,解题时注意设而不求思想的运用.
考点4等差数列与等比数列的综合
例1 已知{an}是等差数列,公差d不为零,前n项和是Sn.若a3,a4,a8成等比数列,则
A.a1d>0,dS4>0 B.a1d<0,dS4<0
C.a1d>0,dS4<0 D.a1d<0,dS4>0
【答案】B
【解析】由a=a3a8,得(a1+2d)(a1+7d)=(a1+3d)2,整理得d(5d+3a1)=0,又d≠0,∴a1=?d,则a1d=?d2<0,又∵S4=4a1+6d=?d,∴dS4=?d2<0,故选B.
【易错点】对三项成等差数列的中项性质应用.
例2 已知数列{an}满足:an+1?an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=,,求数列{bn}的通项公式.
【答案】(1) an=3n+1;(2) bn=×23n+1.
【解析】(1)由已知数列{an}为等差数列,公差为d,则S3=3×4+d=21,解得d=3,
所以数列{an}的通项公式为an=3n+1.
(2)由(1)得bn+1?bn=23n+1.
当n≥2时,bn=(bn?bn?1)+(bn?1?bn?2)+…+(b2?b1)+b1,
所以.
又b1=满足bn=×23n+1,
所以?n∈N*,bn=×23n+1.
【易错点】累加法的联想和使用.
考点5等差数列与等比数列的创新问题
题组一 等差数列与等比数列的新定义问题
例1设Sn为数列{an}的前n项和,若(n∈N*)是非零常数,则称该数列为“和等比数列”.若数列{cn}是首项为2、公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
【答案】4
【解析】由题意可知,数列{cn}的前n项和为,前2n项和为,所以==2+=2+,所以当d=4时,为非零常数.
【易错点】数列新定义型创新题.
【思维点拨】
数列新定义型创新题的一般解题思路:
(1)阅读审清“新定义”;
(2)结合常规的等差数列、等比数列的相关知识,化归、转化到“新定义”的相关知识;
(3)利用“新定义”及常规的数列知识,求解证明相关结论.
题组二 等差数列与等比数列的文化背景问题
例2《九章算术》卷第六《均输》中,提到如下问题:“今有竹九节,下三节容量四升,上四节容量三升.问中间二节欲均容,各多少?”其中“欲均容”的意思是:使容量变化均匀,即每节的容量成等差数列.在这个问题中的中间两节容量分别是
A. 升、升 B. 2升、3升
C. 升、升 D. 升、升
【答案】D
【解析】设从上而下,记第节的容量为升,故,,设公差为,则有,解得,故,,选D.
【易错点】数学文化和数学知识的结合需要学生的应用意识.
考点6公式法求和
题组一 等差数列的求和公式
例1 设等差数列{an}的前n项和为Sn,且满足S17>0,S18<0,则,,…,中最大的项为
A. B.
C. D.
【答案】C
【解析】因为{an}是等差数列,所以S17==17a9>0,所以a9>0,又S18==9(a9+a10)<0,所以a10<0,即该等差数列前9项均是正数项,从第10项开始是负数项,则最大,故选C.
【易错点】等差数列的公差和求和的关系.
题组二 等比数列的求和公式
例2 在等比数列{an}中,a1+an=34,a2·an?1=64,且前n项和Sn=62,则项数n等于
A.4 B.5
C.6 D.7
【答案】B
【解析】设等比数列{an}的公比为q,由题意得a2an?1=a1an=64,
又a1+an=34,解得a1=2,an=32或a1=32,an=2.
当a1=2,an=32时,Sn====62,解得q=2.又an=a1qn?1,所以2×2n?1=2n=32,解得n=5.
同理,当a1=32,an=2时,由Sn====62,解得q=.又an=a1qn?1=32×n?1=2,所以n?1==4,即n?1=4,n=5.
综上,项数n等于5,故选B.
【易错点】等比数列中项性质的求解.
例3 已知等差数列{an}的前n项和为Sn,且S3=9,a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)若an≠a1(当n≥2时),数列{bn}满足bn=2an,求数列{bn}的前n项和Tn.
【答案】(1) an=n+1或an=3;(2) Tn=2n+2?4.
【解析】(1)设等差数列{an}的公差为d.由题意得a=a1a7,即(a1+2d)2=a1(a1+6d),化简得d=a1或d=0.
当d=a1时,S3=3a1+×a1=a1=9,得a1=2,d=1,
∴an=a1+(n?1)d=2+(n?1)=n+1,即an=n+1;
当d=0时,由S3=9,得a1=3,
∴an=3.
综上,an=n+1或an=3.
(2)由题意可知bn==2n+1,
∴b1=4,=2.
∴{bn}是以4为首项,2为公比的等比数列,
∴Tn==2n+2?4.
【易错点】等差数学与等比数列的互相交叉使用.
【思维点拨】
1.两组求和公式
(1)等差数列:;
(2)等比数列:.
2.在进行等差(比)数列项与和的运算时,若条件和结论间的联系不明显,则均可化成关于a1和d(q)的方程组求解,但要注意消元法及整体计算,以减少计算量.
注:在运用等比数列前n项和公式时,一定要注意判断公比q是否为1,切忌盲目套用公式导致失误.
考点7错位相减法求和
例1 已知等比数列的前项和为,若,则数列的前项和为
A. B.
C. D.
【答案】D
【解析】当时,不成立;当时, ,两式相除得,解得, 则,所以,所以,则数列的前项和为
,
,
两式相减得到:,
所以,故选D.
【易错点】注意错位相减的运算步骤.
例2 已知等差数列满足:,,该数列的前三项分别加上1,1,3后成等比数列,.
(1)求数列,的通项公式;
(2)求数列的前n项和.
【答案】(1),bn=;(2) Tn=.
【解析】(1)设等差数列的公差为d,且d>0,
由,,分别加上1,1,3后成等比数列,得,解得d=2,
∴.
∵,
∴,即bn=.
(2)由(1)得an·bn=.
∴Tn=+…+,①
Tn=+…+,②
①?②,得
Tn=+2+…+.
∴Tn===.
【易错点】注意错位相减的运算步骤.
【思维点拨】
错位相减法
适用于各项由一个等差数列和一个等比数列对应项的乘积组成的数列.把Sn=a1+a2+…+an两边同乘以相应等比数列的公比q,得到qSn=a1q+a2q+…+anq,两式错位相减即可求出Sn.
考点8裂项相消法求和
例1 已知数列的前项和,则数列的前6项和为
A. B.
C. D.
【答案】A
【解析】数列的前项和,时,,两式作差得到,当时,也适合上式,所以,所以,裂项求和得到,故答案为A.
【易错点】需要检验n=1时通项公式.
【思维点拨】本题考查的是数列通项公式的求法及数列求和的常用方法.数列通项的求法中有常见的已知和的关系,求的表达式,一般是写出后两式作差得通项,但是这种方法需要检验n=1时通项公式是否适用.数列求和的常用方法有:错位相减、裂项求和、分组求和等.
例2 已知等比数列{an}的前n项和为Sn,且6Sn=3n+1+a(n∈N*).
(1)求a的值及数列{an}的通项公式;
(2)若bn=(1?an)log3(a·an+1),求数列{}的前n项和Tn.
【答案】(1) a=?3,an=3n?1(n∈N*);(2) Tn=.
【解析】(1)∵6Sn=3n+1+a(n∈N*),
∴当n=1时,6S1=6a1=9+a,
当n≥2时,6an=6(Sn?Sn?1)=2×3n,即an=3n?1,
∵{an}是等比数列,
∴a1=1,则9+a=6,得a=?3,
∴数列{an}的通项公式为an=3n?1(n∈N*).
(2)由(1)得bn=(1?an)log3(a·an+1)=(3n?2)(3n+1),
∴Tn=++…+=++…+=(1?+?+…+?)
=.
【易错点】裂项相消法注意分子.
【思维点拨】裂项相消法
将数列的通项分成两个式子的代数和的形式,然后通过累加抵消中间若干项的方法.裂项相消法适用于形如(其中{an}是各项均不为零的等差数列,c为常数)的数列.
考点9 拆项分组法求和
例1 已知函数,且,则
A. B.
C. D.
【答案】A
【解析】由题意可得,,,,,…,
所以,
,
所以.
【易错点】奇数项与偶数项分别求和,每个和都是等差数列的和,从而易于求解.
【思维点拨】数列求和的常用方法:公式法、分组求和法、裂项相消法、并项求和法、倒序相加法等,当遇到数列的通项为的形式时,可以用并项求和法或者用分组求和法,由于本题中,因此我们把奇数项与偶数项分别求和,每个和都是等差数列的和,从而易于求解.
例2 已知等差数列{an}中,a2=5,前4项和S4=28.
(1)求数列{an}的通项公式;
(2)若bn=(?1)nan,求数列{bn}的前2n项和T2n.
【答案】(1) an= 4n?3;(2) T2n=4n.
【解析】(1)设等差数列{an}的公差为d,则由已知条件得
∴
∴an=a1+(n?1)×d=4n?3.
(2)由(1)可得bn=(?1)nan=(?1)n(4n?3),
∴T2n=?1+5?9+13?17+…+(8n?3)=4×n=4n.
【易错点】注意拆项分组是为了合并.
【思维点拨】
拆项分组法
把数列的每一项拆成两项(或多项),再重新组合成两个(或多个)简单的数列,最后分别求和.
考点10 数列求通项
例1 2015·全国卷Ⅱ设Sn是数列{an}的前n项和,且a1=-1,an+1=Sn+1Sn,则Sn= .
【答案】-
【解析】法一:构造法
由已知得an+1=Sn+1-Sn=Sn+1·Sn,
两边同时除以Sn+1·Sn,得-=-1,
故数列是以-1为首项,-1为公差的等差数列,
则=-1+(n-1)×(-1)=-n,
所以Sn=-.
法二:归纳推理法
由a1=-1,an+1=SnSn+1可得a2=S1S2=a1(a1+a2),故a2==,同理可得a3==,a4==,…,由此猜想当n≥2时,有an==-,所以当n≥2时,Sn=a1+a2+…+an=-1++++…+=-.又因为S1=-1也适合上式,所以Sn=-.
【易错点】(1)条件中既有an+1,又有Sn,自然想到用公式an=又因为结果求Sn,所以考虑用公式an+1=Sn+1-Sn换掉an+1,进而得到关于Sn的递推公式,用构造新数列使问题获解.
(2)考虑到填空题的题型特点,由递推关系求出a2,a3,a4,进而发现规律,猜想通项公式an,最后由an求出Sn,当然这需要冒一定风险.
【思维点拨】
1.一般地,对于既有an,又有Sn的数列题,应充分利用公式an=有时将an转化为Sn,有时将Sn转化为an,要根据题中所给条件灵活变动.特别注意的是,公式an=Sn-Sn-1当且仅当n≥2时成立,所以在利用作差法求解数列的通项公式时,应注意对n=1的检验.
2.由递推公式求数列通项的常用方法
(1)形如an+1=an+f(n),常用叠加法,即利用恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)求通项公式.
(2)形如an+1=anf(n),常可采用叠乘法,即利用恒等式an=a1···…·求通项公式.
(3)形如an+1=ban+d(其中b,d为常数,b≠0,1)的数列,常用构造法.其基本思路是:构造an+1+x=b(an+x),则{an+x}是公比为b的等比数列,利用它即可求出an.
(4)形如an+1=(p,q,r是常数)的数列,将其变形为=·+.
若p=r,则是等差数列,且公差为,可用公式求通项;
若p≠r,则再采用(3)的办法求解.
考点11数列的综合应用
题组一 数列与不等式的交汇
例1 设等差数列{an}的前n项和为Sn,已知a1=9,a2为整数,且Sn≤S5.
(1)求{an}的通项公式;
(2)设数列{}的前n项和为Tn,求证:Tn≤.
【答案】(1) an=11?2n;(2)见解析.
【解析】(1)由a1=9,a2为整数可知,等差数列{an}的公差d为整数.
又Sn≤S5,
∴a5≥0,a6≤0,于是9+4d≥0,9+5d≤0,解得?≤d≤?.
∵d为整数,
∴d=?2.
故{an}的通项公式为an=11?2n.
(2)由(1)得,==(?),
∴Tn=[(?)+(?)+…+(?)]=(?).
令bn=,
由函数f(x)=的图象关于点(4.5,0)对称及其单调性,知0<b1<b2<b3<b4,b5<b6<b7<…<0,
∴bn≤b4=1.
∴Tn≤×(1?)=.
【易错点】数列的不等式注意最后的分析.
题组二 数列与函数的交汇
例2 设曲线y=2 018xn+1(n∈N*)在点(1,2 018)处的切线与x轴的交点的横坐标为xn,令,则a1+a2+…+a2 017的值为
A.2 018 B.2 017
C.1 D.?1
【答案】D
【解析】因为y′=2 018(n+1)xn,所以切线方程是y?2 018=2 018(n+1)(x?1),所以xn=,
所以a1+a2+…+a2 017=log2 018(x1·x2·…·x2 017)=log2 018(××…×)==?1.故选D.
【易错点】数列结合了导数和对数的知识,综合性强.
【思维点拨】
数列与不等式的交汇多为不等式恒成立或证明和的范围的形式,在求解时要注意等价转化,即分离参数法与放缩法的技巧应用.
已知函数条件解决数列问题,此类问题一般利用函数的性质、图象研究数列问题;已知数列条件解决函数问题,解决此类问题一般要充分利用数列的范围、公式、求和方法等对式子化简变形.
四、成果巩固
题型一 求等差数列和等比数列的基本量
1.(陕西省2018届高三教学质量检测试题(一))已知等差数列的前项和为,且,.若,则
A.420 B.340
C.?420 D.?340
【答案】D
【解析】根据等差数列的性质得到,
故得到
2.(河南省2018届高三一轮复习诊断例联考高三上学期联考)在等比数列中,若,,则
A. B.
C. D.
【答案】A
【解析】设等比数列的公比为,则,
.故选A.
3.(河北衡水金卷2018届高三高考模拟)已知等差数列的前项和是,且,则下列命题正确的是
A.是常数 B.是常数
C.是常数 D.是常数
【答案】D
【解析】,,为常数,故选D.
题型二等差数列和等比数列的求和基本量求解
1.(安徽省蒙城县第一中学、淮南第一中学等2018届高三上学期“五校”联考)对于数列,定义数列为数列的“倍差数列”,若的“倍差数列”的通项公式为,则数列的前项和__________.
【答案】
【解析】由,且,得,所以数列表示首项为,公差的等差数列,所以,所以,
则,
,
两式相减可得,
解得.
2.(广东省中山市2017?2018学年高三上学期期末复习)等比数列中,已知对任意自然数n,,则等于
A. B.
C. D.以上都不对
【答案】C
【解析】当时,,
当时,,
两式作差可得:,当时,,
综上可得,数列的通项公式为,故,则数列是首项为,公比为的等比数列,其前n项和为.本题选择C选项.
3.(湖北省八校2018届高三上学期第一次联考(12月))已知正项等比数列的前项和为,且,与的等差中项为,则
A. B.
C. D.
【答案】D
【解析】∵,∴,故,又,∴,∴,, ,故选D.
4.(山西省榆社中学2018届高三11月月考)中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,他们各应偿还多少?已知牛、马、羊的主人应偿还升, 升, 升,1斗为10升.则下列判断正确的是
A.依次成公比为2的等比数列,且
B.依次成公比为2的等比数列,且
C.依次成公比为的等比数列,且
D.依次成公比为的等比数列,且
【答案】D
【解析】由条件知,,依次成公比为的等比数列,三者之和为50升,根据等比数列的前n项和,即故答案为D.
题型三数列求和
1.(2018全国新课标Ⅱ文、理)记为等差数列的前项和,已知,.
(1)求的通项公式;
(2)求,并求的最小值.
【答案】(1);(2),最小值为.
【解析】(1)设的公差为,由题意得,
由得.所以的通项公式为.
(2)由(1)得,
当时,取得最小值,最小值为.
2.(2018全国新课标Ⅲ文、理)等比数列中,.
(1)求的通项公式;
(2)记为的前项和.若,求.
【答案】(1)或;(2).
【解析】(1)设数列的公比为,∴,∴.
∴或.
(2)由(1)知,或,
∴或(舍),
∴.
3.(2017新课标Ⅱ)等差数列的前项和为,,,则 .
【答案】
【解析】设等差数列的首项为,公差为,则,
解得,,
∴,所以,
所以.
题型四通项公式求解
1.(2018·陕西六市联考)已知数列{an}中,a1=3,且点Pn(an,an+1)(n∈N*)在直线4x-y+1=0上,则数列{an}的通项公式为________________.
【答案】an=×4n-1-
【解析】因为点Pn(an,an+1)(n∈N*)在直线4x-y+1=0上,
所以4an-an+1+1=0.
所以an+1+=4.
因为a1=3,所以a1+=.
故数列是首项为,公比为4的等比数列.
所以an+=×4n-1,故数列{an}的通项公式为
an=×4n-1-.
2.(2018·武汉调研)数列{an}满足a1=2,an+1=a(an>0,n∈N*),则an=__________.
【答案】
【解析】因为数列{an}满足a1=2,an+1=a(an>0,n∈N*),
所以log2an+1=2log2an,即=2.
又a1=2,所以log2a1=log22=1.
故数列{log2an}是首项为1,公比为2的等比数列.
所以log2an=2n-1,即an=.
3.数列{an}满足a1=2,a2=1,并且=(n≥2),则数列{an}的第100项为( )
A. B.
C. D.
【答案】D
【解析】 因为=(n≥2),所以数列是常数数列,设=k,所以-=,所以=1-=,所以=-+-+…+-+=+=50,所以a100=.
五、课堂小结
1.等差数列和等比数列各有五个量a1,n,d,an,Sn或a1,n,q,an,Sn.一般可以“知三求二”,通过列方程(组)求关键量a1和d(或q),问题可迎刃而解.
2.数列的综合问题通常可以从以下三个角度去考虑:(1)建立基本量的方程(组)求解;(2)巧用等差数列或等比数列的性质求解;(3)构建递推关系求解,有些数列问题还要涉及其它章节的知识求解,如函数的思想等.
3.数列求和
(1) 公式法: 直接运用等差数列、等比数列求和公式;
(2) 化归法: 将已知数列的求和问题化为等差数列、等比数列求和问题;
(3) 倒序相加法: 对前后项有对称性的数列求和;
(4) 错位相减法: 对等比数列与等差数列组合数列求和;
(5) 并项求和法: 将相邻n项合并为一项求和;
(6) 分部求和法:将一个数列分成n部分求和;
(7) 裂项相消法:将数列的通项分解成两项之差,从而在求和时产生相消为零的项的求和方法.
4
1
教材版本 全国通用 课时说明(建议) 120分钟
知识点 数列的概念和表示法,等差、等比数列的概念、性质、前n项和公式; 数列求和的常用方法,数列的通项公式
复习目标 ⑴数列的概念和简单表示法 ①了解数列的概念和几种简单的表示方法(列表、图象、通项公式). ②了解数列是自变量为正整数的一类函数. ⑵等差数列、等比数列 ①理解等差数列、等比数列的概念. ②掌握等差数列、等比数列的通项公式与前项和公式. ③能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题. ④了解等差数列与一次函数、等比数列与指数函数的关系. ⑶掌握数列求和方法.
复习重点 ⑴数列的概念和简单表示法 ⑵等差数列、等比数列 ⑶数列求和方法.
复习难点 ⑴数列的概念和简单表示法 ⑵等差数列、等比数列 ⑶数列求和方法.
一、高考回顾
统计了全国I卷近五年、全国II卷近五年、全国III卷近三年文理共26份试卷.以大题形式考查,全部是在第17题,14年II卷题考查了先放缩再求和,从而证明不等式,有一定难度,其它题均是基本题型,比较容易;以小题形式考查,有1题次出现在第12题(2017理科1卷,考查分组数列求和),2题次出现在题(递推公式求通项,),其它题都是偏容易题型,以数列基本量的换算题型出现次数最多.
重视转化与化归思想,无论是递推公式求通项,还是数列求和,都注重将一般数列转化为等差、等比数列解决;重视函数与方程思想,考查数列的函数特性,利用函数图像、性质等求数列的最大(小)项,数列基本量的换算体现的是设未知数、列方程、解方程的基本思想.
二、知识清单
1.思维导图
下面的思维导图形式呈现本部分的核心知识、核心方法、思维特征、思维载体等内容。
(
用函数方法研究性质
思维载体
数列
数列的概念
等差等比数列
数列通项与求和
核心知识
核心方法
思维特征
符号语言
描述语言
数列
的项数
用离散点研究特征
用通项研究性质
)
2.知识再现
板块一:等差数列与等比数列的基本性质
等差数列:
定义: 一般地,如果一个数列从第项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.这个常数叫做等差数列的公差,通常用字母表示.
通项公式:;
前项和公式:.
等差数列的性质(其中公差为):
⑴,;
⑵若,则有;若,则有(,,,);
⑶在等差数列中,等距离取出若干项也构成一个等差数列,即,,,为等差数列,公差为;
⑷等差数列的项和也构成一个等差数列,即,为等差数列,公差为;
⑸若等差数列的项数为,则有,;若等差数列的项数为奇数,则,且中间项,;
⑹为等差数列,为前项和,则;为等差数列,为前项和,;有.
等比数列:
定义:一般地,如果一个数列从第项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,通常用字母表示.等比数列中的项不为.
通项公式:;前项和公式:.
等比数列的性质(其中公比为):
⑴,;
⑵若,则有;若,则有;
⑶等距离取出若干项也构成一个等比数列,即,,,为等比数列,公比为.
⑷等比数列(公比不为-1)的项和也构成一个等比数列,即,为等比数列,公比为.
板块二:数列的通项公式
常见的已知递推式求通项公式的常用方法:
⑴(其中),则;
⑵(其中),则;
⑶(其中,,是关于的多项式函数),
可设,其中为与的次数相等的多项式函数,各项的系数都待定,通过比较与的各项系数可以确定待定系数;
⑷,其中,,,,.
若,则;
若,则可以设;也可两边同时除以:;
也可两边同时除以:.
板块三:特殊数列求和
1.直接法:即直接用等差、等比数列的求和公式求和.
(1)等差数列的求和公式:
(2)等比数列的求和公式(切记:公比含字母时一定要讨论)
2.公式法:
3.错位相减法:比如
4.裂项相消法:把数列的通项拆成两项之差、正负相消剩下首尾若干项.
常见拆项公式: ;
5.分组求和法:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和.
6.合并求和法:如求的和.
7.倒序相加法:如(C为常数).
8.其它求和法:如归纳猜想法,奇偶法等
三、例题精讲
考点1 等差数列、等比数列的基本运算
题组一 等差数列基本量的计算
例1 设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sn+2?Sn=36,则n=
A.5 B.6
C.7 D.8
【答案】D
【解析】解法一:由题知,Sn+2=(n+2)2,由Sn+2?Sn=36得,(n+2)2?n2=4n+4=36,所以n=8.
解法二:Sn+2?Sn=an+1+an+2=2a1+(2n+1)d=2+2(2n+1)=36,解得n=8.所以选D.
【易错点】对Sn+2?Sn=36,解析为an+2,发生错误。
题组二 等比数列基本量的计算
例2 在各项均为正数的等比数列{an}中,若,则a6的值是________.
【答案】4
【解析】设公比为q(q≠0),∵a2=1,则由得,即,解得q2=2,
∴.
【易错点】忘了条件中的正数的等比数列.
【思维点拨】
等差(比)数列基本量的计算是解决等差(比)数列题型时的基础方法,在高考中常有所体现,多以选择题或填空题的形式呈现,有时也会出现在解答题的第一问中,属基础题.等差(比)数列基本运算的解题思路:
(1)设基本量a1和公差d(公比q).
(2)列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
考点2等差数列、等比数列的判定与证明
题组一 等差数列的判定与证明
例1设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是a和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=?n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
【答案】(1)见解析;(2) 当n=2或n=3时,{an·bn}的最大项的值为6.
【解析】(1)由已知可得2Sn=a+an,且an>0,
当n=1时,2a1=a+a1,解得a1=1;
当n≥2时,有2Sn?1=a+an?1,
所以2an=2Sn?2Sn?1=a?a+an?an?1,
所以a?a=an+an?1,即(an+an?1)(an?an?1)=an+an?1,
因为an+an?1>0,
所以an?an?1=1(n≥2).
故数列{an}是首项为1,公差为1的等差数列.
(2)由(1)可知an=n,
设cn=an·bn,则cn=n(?n+5)=?n2+5n=?2+,
因为n∈N*,
所以当n=2或n=3时,{an·bn}的最大项的值为6.
【易错点】Sn是a和an的等差中项,无法构建一个等式去求解出an。
【思维点拨】
等差数列的判定与证明的方法:
定义法:或是等差数列;
定义变形法:验证是否满足;
等差中项法:为等差数列;
通项公式法:通项公式形如为常数为等差数列;
前n项和公式法:为常数为等差数列.
注意:
(1)若判断一个数列不是等差数列,只需找出三项,使得即可;
(2)如果要证明一个数列是等差数列,则必须用定义法或等差中项法.
题组二 等比数列的判定与证明
例2设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2.
(1)设bn=an+1?2an,证明:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
【答案】(1)见解析;(2) an=(3n?1)·2n?2.
【解析】(1)由a1=1及Sn+1=4an+2,得a1+a2=S2=4a1+2.
∴a2=5,
∴b1=a2?2a1=3.
又
①?②,得an+1=4an?4an?1,
∴an+1?2an=2(an?2an?1).
∵bn=an+1?2an,
∴bn=2bn?1,
故{bn}是首项b1=3,公比为2的等比数列.
(2)由(1)知bn=an+1?2an=3·2n?1,
∴?=,
故是首项为,公差为的等差数列.
∴=+(n?1)·=,
故an=(3n?1)·2n?2.
【易错点】对于bn=an+1?2an,在条件中无法构造出来,等比数列的判定与证明常用的方法不清楚.
【思维点拨】
等比数列的判定与证明常用的方法:
(1)定义法:为常数且数列是等比数列.
(2)等比中项法:数列是等比数列.
(3)通项公式法:数列是等比数列.
(4)前项和公式法:若数列的前项和,则该数列是等比数列.
其中前两种方法是证明等比数列的常用方法,而后两种方法一般用于选择题、填空题中.
注意:
(1)若要判定一个数列不是等比数列,则只需判定存在连续三项不成等比数列即可.
(2)只满足的数列未必是等比数列,要使其成为等比数列还需要.
考点3等差数列、等比数列的性质
题组一 等差数列性质的应用
例1若{an}是等差数列,首项a1>0,a2 016+a2 017>0,a2 016·a2 017<0,则使前n项和Sn>0成立的最大正整数n是
A.2 016 B.2 017
C.4 032 D.4 033
【答案】C
【解析】因为a1>0,a2 016+a2 017>0,a2 016·a2 017<0,所以d<0,a2 016>0,a2 017<0,
所以,,所以使前n项和Sn>0成立的最大正整数n是4 032.
【易错点】等差数列的求和与等差数列的某一项有关系。
题组二 等比数列性质的应用
例2已知数列{an}是等比数列,Sn为其前n项和,若a1+a2+a3=4,a4+a5+a6=8,则S12=
A.40 B.60
C.32 D.50
【答案】B
【解析】由等比数列的性质可知,数列S3,S6?S3,S9?S6,S12?S9是等比数列,即数列4,8,S9?S6,S12?S9是等比数列,因此S12=4+8+16+32=60,选B.
【易错点】,等式不会转化.
【思维点拨】
等差(比)数列的性质是每年高考的热点之一,利用等差(比)数列的性质进行求解可使题目减少运算量,题型以选择题或填空题为主,难度不大,属中低档题.
应用等差数列性质的注意点:
(1)熟练掌握等差数列性质的实质
等差数列的性质是等差数列的定义、通项公式以及前n项和公式等基础知识的推广与变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决许多等差数列问题.
(2)应用等差数列的性质解答问题的关键
寻找项数之间的关系,但要注意性质运用的条件,如若,则
,需要当序号之和相等、项数相同时才成立,再比如只有当等差数列{an}的前n项和Sn中的n为奇数时,才有Sn=na中成立.
应用等比数列性质时的注意点:
(1)在解决等比数列的有关问题时,要注意挖掘隐含条件,利用性质,特别是性质“若m+n=p+q,则am·an=ap·aq”,可以减少运算量,提高解题速度.
(2)在应用相应性质解题时,要注意性质成立的前提条件,有时需要进行适当变形.此外,解题时注意设而不求思想的运用.
考点4等差数列与等比数列的综合
例1 已知{an}是等差数列,公差d不为零,前n项和是Sn.若a3,a4,a8成等比数列,则
A.a1d>0,dS4>0 B.a1d<0,dS4<0
C.a1d>0,dS4<0 D.a1d<0,dS4>0
【答案】B
【解析】由a=a3a8,得(a1+2d)(a1+7d)=(a1+3d)2,整理得d(5d+3a1)=0,又d≠0,∴a1=?d,则a1d=?d2<0,又∵S4=4a1+6d=?d,∴dS4=?d2<0,故选B.
【易错点】对三项成等差数列的中项性质应用.
例2 已知数列{an}满足:an+1?an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=,,求数列{bn}的通项公式.
【答案】(1) an=3n+1;(2) bn=×23n+1.
【解析】(1)由已知数列{an}为等差数列,公差为d,则S3=3×4+d=21,解得d=3,
所以数列{an}的通项公式为an=3n+1.
(2)由(1)得bn+1?bn=23n+1.
当n≥2时,bn=(bn?bn?1)+(bn?1?bn?2)+…+(b2?b1)+b1,
所以.
又b1=满足bn=×23n+1,
所以?n∈N*,bn=×23n+1.
【易错点】累加法的联想和使用.
考点5等差数列与等比数列的创新问题
题组一 等差数列与等比数列的新定义问题
例1设Sn为数列{an}的前n项和,若(n∈N*)是非零常数,则称该数列为“和等比数列”.若数列{cn}是首项为2、公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
【答案】4
【解析】由题意可知,数列{cn}的前n项和为,前2n项和为,所以==2+=2+,所以当d=4时,为非零常数.
【易错点】数列新定义型创新题.
【思维点拨】
数列新定义型创新题的一般解题思路:
(1)阅读审清“新定义”;
(2)结合常规的等差数列、等比数列的相关知识,化归、转化到“新定义”的相关知识;
(3)利用“新定义”及常规的数列知识,求解证明相关结论.
题组二 等差数列与等比数列的文化背景问题
例2《九章算术》卷第六《均输》中,提到如下问题:“今有竹九节,下三节容量四升,上四节容量三升.问中间二节欲均容,各多少?”其中“欲均容”的意思是:使容量变化均匀,即每节的容量成等差数列.在这个问题中的中间两节容量分别是
A. 升、升 B. 2升、3升
C. 升、升 D. 升、升
【答案】D
【解析】设从上而下,记第节的容量为升,故,,设公差为,则有,解得,故,,选D.
【易错点】数学文化和数学知识的结合需要学生的应用意识.
考点6公式法求和
题组一 等差数列的求和公式
例1 设等差数列{an}的前n项和为Sn,且满足S17>0,S18<0,则,,…,中最大的项为
A. B.
C. D.
【答案】C
【解析】因为{an}是等差数列,所以S17==17a9>0,所以a9>0,又S18==9(a9+a10)<0,所以a10<0,即该等差数列前9项均是正数项,从第10项开始是负数项,则最大,故选C.
【易错点】等差数列的公差和求和的关系.
题组二 等比数列的求和公式
例2 在等比数列{an}中,a1+an=34,a2·an?1=64,且前n项和Sn=62,则项数n等于
A.4 B.5
C.6 D.7
【答案】B
【解析】设等比数列{an}的公比为q,由题意得a2an?1=a1an=64,
又a1+an=34,解得a1=2,an=32或a1=32,an=2.
当a1=2,an=32时,Sn====62,解得q=2.又an=a1qn?1,所以2×2n?1=2n=32,解得n=5.
同理,当a1=32,an=2时,由Sn====62,解得q=.又an=a1qn?1=32×n?1=2,所以n?1==4,即n?1=4,n=5.
综上,项数n等于5,故选B.
【易错点】等比数列中项性质的求解.
例3 已知等差数列{an}的前n项和为Sn,且S3=9,a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)若an≠a1(当n≥2时),数列{bn}满足bn=2an,求数列{bn}的前n项和Tn.
【答案】(1) an=n+1或an=3;(2) Tn=2n+2?4.
【解析】(1)设等差数列{an}的公差为d.由题意得a=a1a7,即(a1+2d)2=a1(a1+6d),化简得d=a1或d=0.
当d=a1时,S3=3a1+×a1=a1=9,得a1=2,d=1,
∴an=a1+(n?1)d=2+(n?1)=n+1,即an=n+1;
当d=0时,由S3=9,得a1=3,
∴an=3.
综上,an=n+1或an=3.
(2)由题意可知bn==2n+1,
∴b1=4,=2.
∴{bn}是以4为首项,2为公比的等比数列,
∴Tn==2n+2?4.
【易错点】等差数学与等比数列的互相交叉使用.
【思维点拨】
1.两组求和公式
(1)等差数列:;
(2)等比数列:.
2.在进行等差(比)数列项与和的运算时,若条件和结论间的联系不明显,则均可化成关于a1和d(q)的方程组求解,但要注意消元法及整体计算,以减少计算量.
注:在运用等比数列前n项和公式时,一定要注意判断公比q是否为1,切忌盲目套用公式导致失误.
考点7错位相减法求和
例1 已知等比数列的前项和为,若,则数列的前项和为
A. B.
C. D.
【答案】D
【解析】当时,不成立;当时, ,两式相除得,解得, 则,所以,所以,则数列的前项和为
,
,
两式相减得到:,
所以,故选D.
【易错点】注意错位相减的运算步骤.
例2 已知等差数列满足:,,该数列的前三项分别加上1,1,3后成等比数列,.
(1)求数列,的通项公式;
(2)求数列的前n项和.
【答案】(1),bn=;(2) Tn=.
【解析】(1)设等差数列的公差为d,且d>0,
由,,分别加上1,1,3后成等比数列,得,解得d=2,
∴.
∵,
∴,即bn=.
(2)由(1)得an·bn=.
∴Tn=+…+,①
Tn=+…+,②
①?②,得
Tn=+2+…+.
∴Tn===.
【易错点】注意错位相减的运算步骤.
【思维点拨】
错位相减法
适用于各项由一个等差数列和一个等比数列对应项的乘积组成的数列.把Sn=a1+a2+…+an两边同乘以相应等比数列的公比q,得到qSn=a1q+a2q+…+anq,两式错位相减即可求出Sn.
考点8裂项相消法求和
例1 已知数列的前项和,则数列的前6项和为
A. B.
C. D.
【答案】A
【解析】数列的前项和,时,,两式作差得到,当时,也适合上式,所以,所以,裂项求和得到,故答案为A.
【易错点】需要检验n=1时通项公式.
【思维点拨】本题考查的是数列通项公式的求法及数列求和的常用方法.数列通项的求法中有常见的已知和的关系,求的表达式,一般是写出后两式作差得通项,但是这种方法需要检验n=1时通项公式是否适用.数列求和的常用方法有:错位相减、裂项求和、分组求和等.
例2 已知等比数列{an}的前n项和为Sn,且6Sn=3n+1+a(n∈N*).
(1)求a的值及数列{an}的通项公式;
(2)若bn=(1?an)log3(a·an+1),求数列{}的前n项和Tn.
【答案】(1) a=?3,an=3n?1(n∈N*);(2) Tn=.
【解析】(1)∵6Sn=3n+1+a(n∈N*),
∴当n=1时,6S1=6a1=9+a,
当n≥2时,6an=6(Sn?Sn?1)=2×3n,即an=3n?1,
∵{an}是等比数列,
∴a1=1,则9+a=6,得a=?3,
∴数列{an}的通项公式为an=3n?1(n∈N*).
(2)由(1)得bn=(1?an)log3(a·an+1)=(3n?2)(3n+1),
∴Tn=++…+=++…+=(1?+?+…+?)
=.
【易错点】裂项相消法注意分子.
【思维点拨】裂项相消法
将数列的通项分成两个式子的代数和的形式,然后通过累加抵消中间若干项的方法.裂项相消法适用于形如(其中{an}是各项均不为零的等差数列,c为常数)的数列.
考点9 拆项分组法求和
例1 已知函数,且,则
A. B.
C. D.
【答案】A
【解析】由题意可得,,,,,…,
所以,
,
所以.
【易错点】奇数项与偶数项分别求和,每个和都是等差数列的和,从而易于求解.
【思维点拨】数列求和的常用方法:公式法、分组求和法、裂项相消法、并项求和法、倒序相加法等,当遇到数列的通项为的形式时,可以用并项求和法或者用分组求和法,由于本题中,因此我们把奇数项与偶数项分别求和,每个和都是等差数列的和,从而易于求解.
例2 已知等差数列{an}中,a2=5,前4项和S4=28.
(1)求数列{an}的通项公式;
(2)若bn=(?1)nan,求数列{bn}的前2n项和T2n.
【答案】(1) an= 4n?3;(2) T2n=4n.
【解析】(1)设等差数列{an}的公差为d,则由已知条件得
∴
∴an=a1+(n?1)×d=4n?3.
(2)由(1)可得bn=(?1)nan=(?1)n(4n?3),
∴T2n=?1+5?9+13?17+…+(8n?3)=4×n=4n.
【易错点】注意拆项分组是为了合并.
【思维点拨】
拆项分组法
把数列的每一项拆成两项(或多项),再重新组合成两个(或多个)简单的数列,最后分别求和.
考点10 数列求通项
例1 2015·全国卷Ⅱ设Sn是数列{an}的前n项和,且a1=-1,an+1=Sn+1Sn,则Sn= .
【答案】-
【解析】法一:构造法
由已知得an+1=Sn+1-Sn=Sn+1·Sn,
两边同时除以Sn+1·Sn,得-=-1,
故数列是以-1为首项,-1为公差的等差数列,
则=-1+(n-1)×(-1)=-n,
所以Sn=-.
法二:归纳推理法
由a1=-1,an+1=SnSn+1可得a2=S1S2=a1(a1+a2),故a2==,同理可得a3==,a4==,…,由此猜想当n≥2时,有an==-,所以当n≥2时,Sn=a1+a2+…+an=-1++++…+=-.又因为S1=-1也适合上式,所以Sn=-.
【易错点】(1)条件中既有an+1,又有Sn,自然想到用公式an=又因为结果求Sn,所以考虑用公式an+1=Sn+1-Sn换掉an+1,进而得到关于Sn的递推公式,用构造新数列使问题获解.
(2)考虑到填空题的题型特点,由递推关系求出a2,a3,a4,进而发现规律,猜想通项公式an,最后由an求出Sn,当然这需要冒一定风险.
【思维点拨】
1.一般地,对于既有an,又有Sn的数列题,应充分利用公式an=有时将an转化为Sn,有时将Sn转化为an,要根据题中所给条件灵活变动.特别注意的是,公式an=Sn-Sn-1当且仅当n≥2时成立,所以在利用作差法求解数列的通项公式时,应注意对n=1的检验.
2.由递推公式求数列通项的常用方法
(1)形如an+1=an+f(n),常用叠加法,即利用恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)求通项公式.
(2)形如an+1=anf(n),常可采用叠乘法,即利用恒等式an=a1···…·求通项公式.
(3)形如an+1=ban+d(其中b,d为常数,b≠0,1)的数列,常用构造法.其基本思路是:构造an+1+x=b(an+x),则{an+x}是公比为b的等比数列,利用它即可求出an.
(4)形如an+1=(p,q,r是常数)的数列,将其变形为=·+.
若p=r,则是等差数列,且公差为,可用公式求通项;
若p≠r,则再采用(3)的办法求解.
考点11数列的综合应用
题组一 数列与不等式的交汇
例1 设等差数列{an}的前n项和为Sn,已知a1=9,a2为整数,且Sn≤S5.
(1)求{an}的通项公式;
(2)设数列{}的前n项和为Tn,求证:Tn≤.
【答案】(1) an=11?2n;(2)见解析.
【解析】(1)由a1=9,a2为整数可知,等差数列{an}的公差d为整数.
又Sn≤S5,
∴a5≥0,a6≤0,于是9+4d≥0,9+5d≤0,解得?≤d≤?.
∵d为整数,
∴d=?2.
故{an}的通项公式为an=11?2n.
(2)由(1)得,==(?),
∴Tn=[(?)+(?)+…+(?)]=(?).
令bn=,
由函数f(x)=的图象关于点(4.5,0)对称及其单调性,知0<b1<b2<b3<b4,b5<b6<b7<…<0,
∴bn≤b4=1.
∴Tn≤×(1?)=.
【易错点】数列的不等式注意最后的分析.
题组二 数列与函数的交汇
例2 设曲线y=2 018xn+1(n∈N*)在点(1,2 018)处的切线与x轴的交点的横坐标为xn,令,则a1+a2+…+a2 017的值为
A.2 018 B.2 017
C.1 D.?1
【答案】D
【解析】因为y′=2 018(n+1)xn,所以切线方程是y?2 018=2 018(n+1)(x?1),所以xn=,
所以a1+a2+…+a2 017=log2 018(x1·x2·…·x2 017)=log2 018(××…×)==?1.故选D.
【易错点】数列结合了导数和对数的知识,综合性强.
【思维点拨】
数列与不等式的交汇多为不等式恒成立或证明和的范围的形式,在求解时要注意等价转化,即分离参数法与放缩法的技巧应用.
已知函数条件解决数列问题,此类问题一般利用函数的性质、图象研究数列问题;已知数列条件解决函数问题,解决此类问题一般要充分利用数列的范围、公式、求和方法等对式子化简变形.
四、成果巩固
题型一 求等差数列和等比数列的基本量
1.(陕西省2018届高三教学质量检测试题(一))已知等差数列的前项和为,且,.若,则
A.420 B.340
C.?420 D.?340
【答案】D
【解析】根据等差数列的性质得到,
故得到
2.(河南省2018届高三一轮复习诊断例联考高三上学期联考)在等比数列中,若,,则
A. B.
C. D.
【答案】A
【解析】设等比数列的公比为,则,
.故选A.
3.(河北衡水金卷2018届高三高考模拟)已知等差数列的前项和是,且,则下列命题正确的是
A.是常数 B.是常数
C.是常数 D.是常数
【答案】D
【解析】,,为常数,故选D.
题型二等差数列和等比数列的求和基本量求解
1.(安徽省蒙城县第一中学、淮南第一中学等2018届高三上学期“五校”联考)对于数列,定义数列为数列的“倍差数列”,若的“倍差数列”的通项公式为,则数列的前项和__________.
【答案】
【解析】由,且,得,所以数列表示首项为,公差的等差数列,所以,所以,
则,
,
两式相减可得,
解得.
2.(广东省中山市2017?2018学年高三上学期期末复习)等比数列中,已知对任意自然数n,,则等于
A. B.
C. D.以上都不对
【答案】C
【解析】当时,,
当时,,
两式作差可得:,当时,,
综上可得,数列的通项公式为,故,则数列是首项为,公比为的等比数列,其前n项和为.本题选择C选项.
3.(湖北省八校2018届高三上学期第一次联考(12月))已知正项等比数列的前项和为,且,与的等差中项为,则
A. B.
C. D.
【答案】D
【解析】∵,∴,故,又,∴,∴,, ,故选D.
4.(山西省榆社中学2018届高三11月月考)中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,他们各应偿还多少?已知牛、马、羊的主人应偿还升, 升, 升,1斗为10升.则下列判断正确的是
A.依次成公比为2的等比数列,且
B.依次成公比为2的等比数列,且
C.依次成公比为的等比数列,且
D.依次成公比为的等比数列,且
【答案】D
【解析】由条件知,,依次成公比为的等比数列,三者之和为50升,根据等比数列的前n项和,即故答案为D.
题型三数列求和
1.(2018全国新课标Ⅱ文、理)记为等差数列的前项和,已知,.
(1)求的通项公式;
(2)求,并求的最小值.
【答案】(1);(2),最小值为.
【解析】(1)设的公差为,由题意得,
由得.所以的通项公式为.
(2)由(1)得,
当时,取得最小值,最小值为.
2.(2018全国新课标Ⅲ文、理)等比数列中,.
(1)求的通项公式;
(2)记为的前项和.若,求.
【答案】(1)或;(2).
【解析】(1)设数列的公比为,∴,∴.
∴或.
(2)由(1)知,或,
∴或(舍),
∴.
3.(2017新课标Ⅱ)等差数列的前项和为,,,则 .
【答案】
【解析】设等差数列的首项为,公差为,则,
解得,,
∴,所以,
所以.
题型四通项公式求解
1.(2018·陕西六市联考)已知数列{an}中,a1=3,且点Pn(an,an+1)(n∈N*)在直线4x-y+1=0上,则数列{an}的通项公式为________________.
【答案】an=×4n-1-
【解析】因为点Pn(an,an+1)(n∈N*)在直线4x-y+1=0上,
所以4an-an+1+1=0.
所以an+1+=4.
因为a1=3,所以a1+=.
故数列是首项为,公比为4的等比数列.
所以an+=×4n-1,故数列{an}的通项公式为
an=×4n-1-.
2.(2018·武汉调研)数列{an}满足a1=2,an+1=a(an>0,n∈N*),则an=__________.
【答案】
【解析】因为数列{an}满足a1=2,an+1=a(an>0,n∈N*),
所以log2an+1=2log2an,即=2.
又a1=2,所以log2a1=log22=1.
故数列{log2an}是首项为1,公比为2的等比数列.
所以log2an=2n-1,即an=.
3.数列{an}满足a1=2,a2=1,并且=(n≥2),则数列{an}的第100项为( )
A. B.
C. D.
【答案】D
【解析】 因为=(n≥2),所以数列是常数数列,设=k,所以-=,所以=1-=,所以=-+-+…+-+=+=50,所以a100=.
五、课堂小结
1.等差数列和等比数列各有五个量a1,n,d,an,Sn或a1,n,q,an,Sn.一般可以“知三求二”,通过列方程(组)求关键量a1和d(或q),问题可迎刃而解.
2.数列的综合问题通常可以从以下三个角度去考虑:(1)建立基本量的方程(组)求解;(2)巧用等差数列或等比数列的性质求解;(3)构建递推关系求解,有些数列问题还要涉及其它章节的知识求解,如函数的思想等.
3.数列求和
(1) 公式法: 直接运用等差数列、等比数列求和公式;
(2) 化归法: 将已知数列的求和问题化为等差数列、等比数列求和问题;
(3) 倒序相加法: 对前后项有对称性的数列求和;
(4) 错位相减法: 对等比数列与等差数列组合数列求和;
(5) 并项求和法: 将相邻n项合并为一项求和;
(6) 分部求和法:将一个数列分成n部分求和;
(7) 裂项相消法:将数列的通项分解成两项之差,从而在求和时产生相消为零的项的求和方法.
4
1
同课章节目录
