江西省南昌市八一中学、洪都中学、麻丘高中等七校2018-2019学年高一下学期期中考试数学试题
文档属性
| 名称 | 江西省南昌市八一中学、洪都中学、麻丘高中等七校2018-2019学年高一下学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-06 18:28:13 | ||
图片预览



文档简介
2018~2019学年度第二学期高一数学期中联考试卷
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)
1.若,则下列不等式不成立的是(?? ?)
A. B. C. D.
2. 若且,则下列四个数中最大的是( )
A. B. C.2ab D.
3.在△ABC中,,则cosB的值为( )
A. B. C. D.
4.设等差数列的前项和,若,则( )
A.15 B.27 C.18 D.12
5.中,若,则的形状为( )
A.直角三角形 B.等腰或直角三角形 C.等边三角形 D.等腰三角形
6.在公差不为0的等差数列中,成等比数列,则公差=( )
A. B. C. D.1
7.在 中,,则满足上述条件的三角形有( )
A.无数个 B.2个 C.0个 D.1个
8.若不等式的解集为,则关于x的不等式的解集为( )
A.(-5,3) B. C.(-3,5) D.
9.在等比数列中,,则=
A.或 B. C.或 D.或
10.设若是与的等比中项,则的最小值为( )
A.12 B.4 C. D.
11.在△ABC中,已知b=1,,,则=( )
A.1或 B.2 C.1 D.2或
12.已知为等差数列的前项和,若且有最小值,则使前项和成立的最大自然数为( )
A.4038 B.4039 C. 4040 D.4041
二、填空题(本大题共4个小题. 每小题5分,共20分)
13.不等式的解集为
14.已知数列中,,且,则数列的通项公式=
15.不等式对任意的恒成立,则的取值范围为
16.下列说法中:
①若,满足,则的最大值为4;
②若,则函数的最小值为3;
③若,满足,则的最大值为;
④若,满足,则的最小值为2;
⑤函数的最小值为9.
正确的有________.(把你认为正确的序号全部写上)
三、解答题(本大题共6小题,共70分.解答题应根据要求写出必要的文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知等差数列满足 .
(1) 求通项公式;
(2) 设等比数列满足,求的前项和.
18.(本题满分12分)
在中,角的对边分别为,且
(1)求角的大小;
(2)若,求周长的最大值
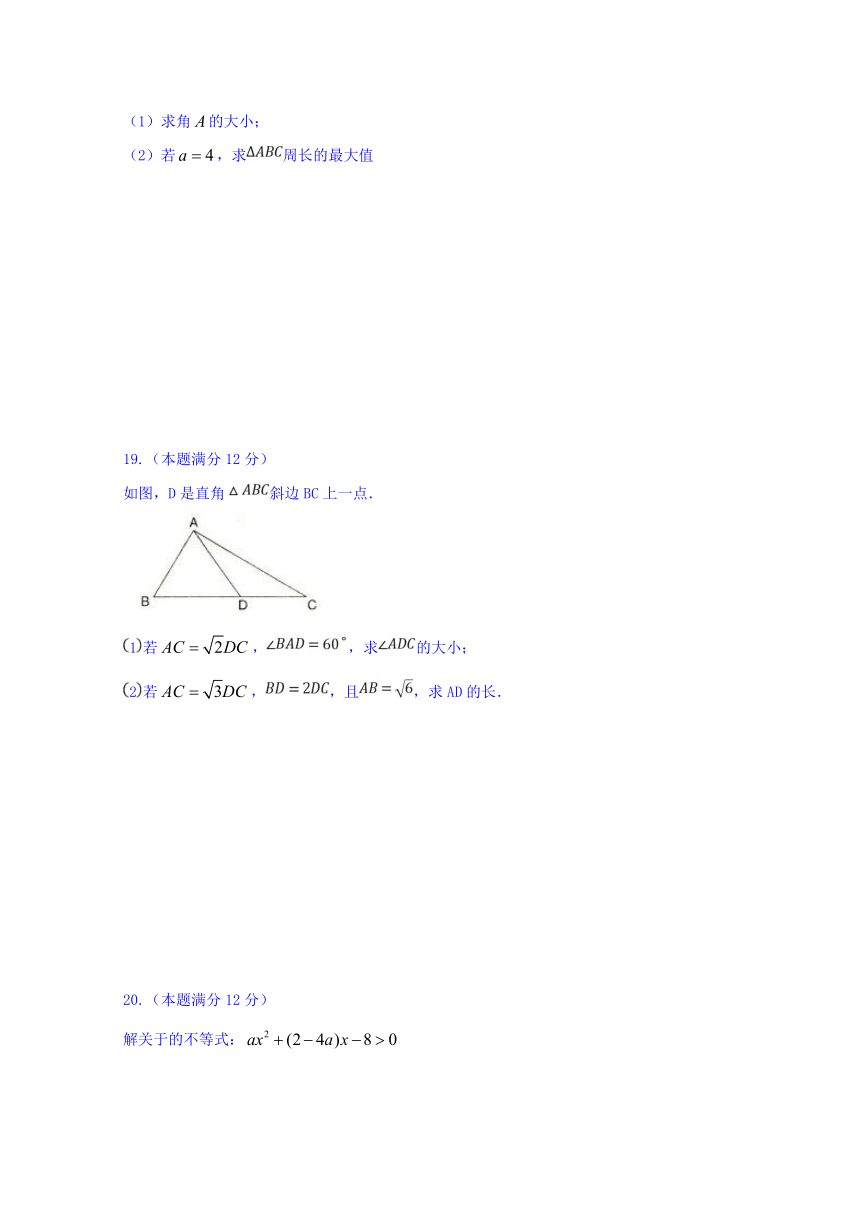
19.(本题满分12分)
如图,D是直角斜边BC上一点.
1若,,求的大小;
2若,,且,求AD的长.
20.(本题满分12分)
解关于的不等式:
21.(本题满分12分)
2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
22.(本题满分12分)
已知正项数列的首项,前项和满足.
(1)求数列的通项公式;
(2)记数列的前项和为,若对任意的,不等式恒成立,求实数的取值范围.
高一数学下学期期中联考参考答案
一、选择题(5分×12=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
B
A
D
C
D
C
A
D
C
B
二、填空题(5分×4=20分)
13. 14.
15. 16. ③④⑤
三、解答题(共70分)
17.解:(1)由得,---------------- 4分
故的通项公式.---------------- 5分
(2)由(1)得.
设的公比为,则,从而,---------------- 8分
故的前项和.---------------- 10分
18.解析:(1)因为
所以由正弦定理可得
,
即,
因为,
所以即.---------------- 6分
(2)由(1)可得,则
,即---------------- 10分
当且仅当时取最大值
故当为等腰三角形,周长最大为---------------- 12分
19.解:1,,,
在中,由正弦定理可得:,
,
---------------- 6分
2,,
在中,由勾股定理可得:,可得:,
,,,
令,由余弦定理:
在中,,
在中,,
可得:,
解得:,可得:---------------- 12分
20.解:可得,
当时,不等式的解为;---------------- 2分
当时,不等式的解为或---------------- 5分
当时, 即
(1)当即时,不等式的解为,
(2)当即时,不等式的解为,
(3)当即时,不等式的解集为空集---------------- 12分
21.解 :(1)依题得: (xN*)
---------------- 6分
(2)
当且仅当时,即x=15时等号成立.
使用15年后平均盈利额达到最大值,该厂商盈利额为1500万元.-------------- 12分
22.解:(1)当时,,∴,即,
所以数列是首项为1,公差为的等差数列,
故,
(),
因此.---------------- 6分
(2)当时,,
∴,
又∵,∴,解得或.
即所求实数的范围是或.---------------- 12分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)
1.若,则下列不等式不成立的是(?? ?)
A. B. C. D.
2. 若且,则下列四个数中最大的是( )
A. B. C.2ab D.
3.在△ABC中,,则cosB的值为( )
A. B. C. D.
4.设等差数列的前项和,若,则( )
A.15 B.27 C.18 D.12
5.中,若,则的形状为( )
A.直角三角形 B.等腰或直角三角形 C.等边三角形 D.等腰三角形
6.在公差不为0的等差数列中,成等比数列,则公差=( )
A. B. C. D.1
7.在 中,,则满足上述条件的三角形有( )
A.无数个 B.2个 C.0个 D.1个
8.若不等式的解集为,则关于x的不等式的解集为( )
A.(-5,3) B. C.(-3,5) D.
9.在等比数列中,,则=
A.或 B. C.或 D.或
10.设若是与的等比中项,则的最小值为( )
A.12 B.4 C. D.
11.在△ABC中,已知b=1,,,则=( )
A.1或 B.2 C.1 D.2或
12.已知为等差数列的前项和,若且有最小值,则使前项和成立的最大自然数为( )
A.4038 B.4039 C. 4040 D.4041
二、填空题(本大题共4个小题. 每小题5分,共20分)
13.不等式的解集为
14.已知数列中,,且,则数列的通项公式=
15.不等式对任意的恒成立,则的取值范围为
16.下列说法中:
①若,满足,则的最大值为4;
②若,则函数的最小值为3;
③若,满足,则的最大值为;
④若,满足,则的最小值为2;
⑤函数的最小值为9.
正确的有________.(把你认为正确的序号全部写上)
三、解答题(本大题共6小题,共70分.解答题应根据要求写出必要的文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知等差数列满足 .
(1) 求通项公式;
(2) 设等比数列满足,求的前项和.
18.(本题满分12分)
在中,角的对边分别为,且
(1)求角的大小;
(2)若,求周长的最大值
19.(本题满分12分)
如图,D是直角斜边BC上一点.
1若,,求的大小;
2若,,且,求AD的长.
20.(本题满分12分)
解关于的不等式:
21.(本题满分12分)
2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
22.(本题满分12分)
已知正项数列的首项,前项和满足.
(1)求数列的通项公式;
(2)记数列的前项和为,若对任意的,不等式恒成立,求实数的取值范围.
高一数学下学期期中联考参考答案
一、选择题(5分×12=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
B
A
D
C
D
C
A
D
C
B
二、填空题(5分×4=20分)
13. 14.
15. 16. ③④⑤
三、解答题(共70分)
17.解:(1)由得,---------------- 4分
故的通项公式.---------------- 5分
(2)由(1)得.
设的公比为,则,从而,---------------- 8分
故的前项和.---------------- 10分
18.解析:(1)因为
所以由正弦定理可得
,
即,
因为,
所以即.---------------- 6分
(2)由(1)可得,则
,即---------------- 10分
当且仅当时取最大值
故当为等腰三角形,周长最大为---------------- 12分
19.解:1,,,
在中,由正弦定理可得:,
,
---------------- 6分
2,,
在中,由勾股定理可得:,可得:,
,,,
令,由余弦定理:
在中,,
在中,,
可得:,
解得:,可得:---------------- 12分
20.解:可得,
当时,不等式的解为;---------------- 2分
当时,不等式的解为或---------------- 5分
当时, 即
(1)当即时,不等式的解为,
(2)当即时,不等式的解为,
(3)当即时,不等式的解集为空集---------------- 12分
21.解 :(1)依题得: (xN*)
---------------- 6分
(2)
当且仅当时,即x=15时等号成立.
使用15年后平均盈利额达到最大值,该厂商盈利额为1500万元.-------------- 12分
22.解:(1)当时,,∴,即,
所以数列是首项为1,公差为的等差数列,
故,
(),
因此.---------------- 6分
(2)当时,,
∴,
又∵,∴,解得或.
即所求实数的范围是或.---------------- 12分
同课章节目录
