6.4正比例和反比例练习 课件(14张ppt)
文档属性
| 名称 | 6.4正比例和反比例练习 课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 818.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-07 00:00:00 | ||
图片预览




文档简介
课件14张PPT。正比例和反比例练习想一想:1、我们已经学过哪些有关比例的知识?
举例说明比例的意义,比例的性质,比例 尺的意义。
2、什么样的两种量成正比例或反比例关系?
判断两种量是否成正比例或反比例关系时,关键要看什么?1、在被除数、除数、商这三种量中,当( )一定时,( )与( )成正比例;当( )一定时,( )与( )成反比例。
2、当 a × b = c( a、b、c 为三种量,且均不为0)。 ( )一定,( )与( )成( )比例; ( )一定,( )与( )成( )比例; ( )一定,( )与( )成( )比例。
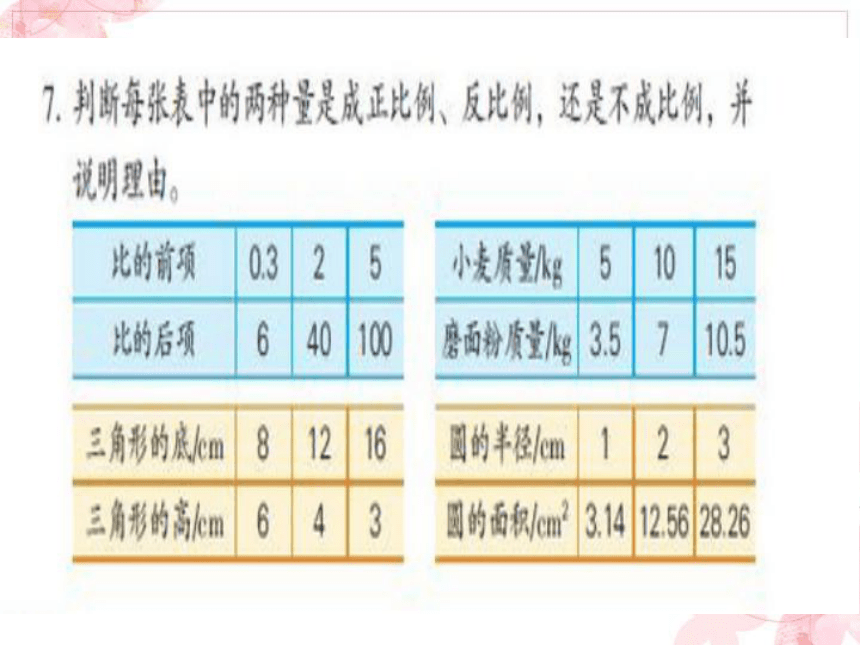
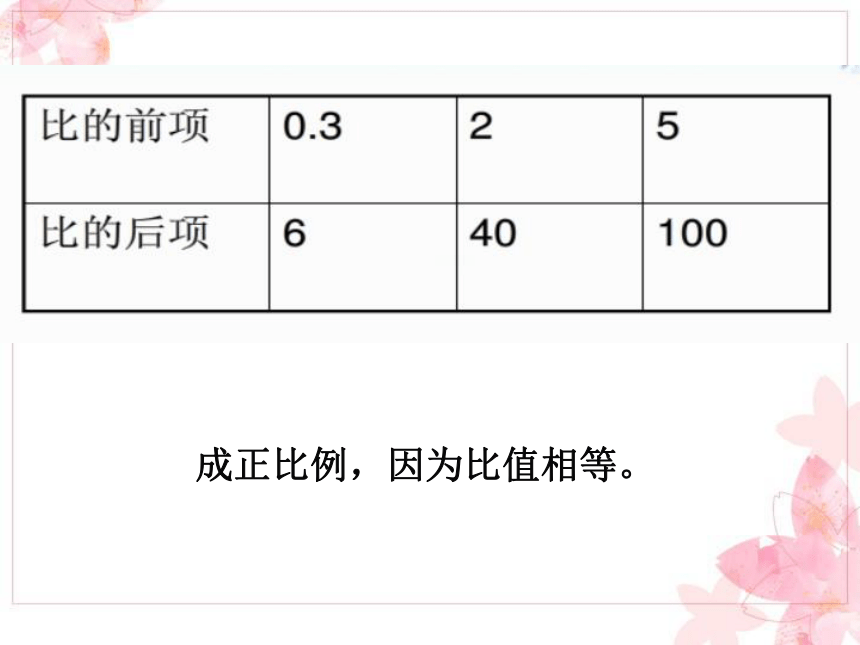
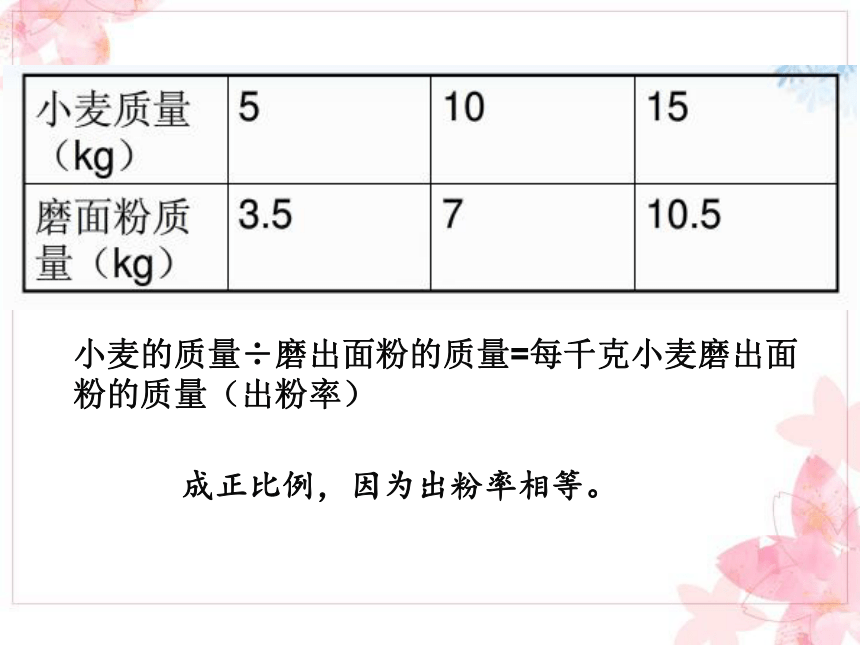
3、在圆柱的侧面积、底面周长、高这三种量中,当底面周长一定时,( )与( )成( )比例;当高一定时,( )与( )成( )比例;当侧面积一定时,( )与( )成( )比例。 成正比例,因为比值相等。成正比例,因为出粉率相等。小麦的质量÷磨出面粉的质量=每千克小麦磨出面粉的质量(出粉率)成反比例,因为面积(乘积)相等。不成比例。S=πr2(1)反比例。每步的平均长度越长步数越少(距离一定)
(2)正比例。压路面积/滚动的转数=滚筒侧面积(一定)
(3)正比例。麦地面积/收割时间=每小时收割面积(一定)
(4)既不成正比例,也不成反比例
(5)反比例。xy=10(一定)答:
(1)行程路程÷耗油量=每升油行驶的路程(一定),所以这辆汽车行驶的路程和耗油量成正比例。
(2)根据图像判断,行驶75千米大约耗油6升。用图像表示正比例关系时,如果根据一组数据描出的点在这条直线上,说明这组数据的比的比值与成正比例关系的两种量的比值相等;如果所描出的点不在这条直线上,说明它们的比值不相等。小结:今天复习了哪些内容?你有哪些收获?思考题:1、甲、乙两车同时从A、B两地出发,相向而行,在距离A、B两地中点8千米处相遇。已知甲车行驶的速度是乙车的 ,求A、B两地之间的公路长。
2、甲、乙两车同时从A、B两个城市出发,相向而行,经过8小时相遇。相遇后,甲车继续向前行驶5小时到达B城。已知甲车每小时比乙车快27千米,求A、B两个城市间的公路长。
举例说明比例的意义,比例的性质,比例 尺的意义。
2、什么样的两种量成正比例或反比例关系?
判断两种量是否成正比例或反比例关系时,关键要看什么?1、在被除数、除数、商这三种量中,当( )一定时,( )与( )成正比例;当( )一定时,( )与( )成反比例。
2、当 a × b = c( a、b、c 为三种量,且均不为0)。 ( )一定,( )与( )成( )比例; ( )一定,( )与( )成( )比例; ( )一定,( )与( )成( )比例。
3、在圆柱的侧面积、底面周长、高这三种量中,当底面周长一定时,( )与( )成( )比例;当高一定时,( )与( )成( )比例;当侧面积一定时,( )与( )成( )比例。 成正比例,因为比值相等。成正比例,因为出粉率相等。小麦的质量÷磨出面粉的质量=每千克小麦磨出面粉的质量(出粉率)成反比例,因为面积(乘积)相等。不成比例。S=πr2(1)反比例。每步的平均长度越长步数越少(距离一定)
(2)正比例。压路面积/滚动的转数=滚筒侧面积(一定)
(3)正比例。麦地面积/收割时间=每小时收割面积(一定)
(4)既不成正比例,也不成反比例
(5)反比例。xy=10(一定)答:
(1)行程路程÷耗油量=每升油行驶的路程(一定),所以这辆汽车行驶的路程和耗油量成正比例。
(2)根据图像判断,行驶75千米大约耗油6升。用图像表示正比例关系时,如果根据一组数据描出的点在这条直线上,说明这组数据的比的比值与成正比例关系的两种量的比值相等;如果所描出的点不在这条直线上,说明它们的比值不相等。小结:今天复习了哪些内容?你有哪些收获?思考题:1、甲、乙两车同时从A、B两地出发,相向而行,在距离A、B两地中点8千米处相遇。已知甲车行驶的速度是乙车的 ,求A、B两地之间的公路长。
2、甲、乙两车同时从A、B两个城市出发,相向而行,经过8小时相遇。相遇后,甲车继续向前行驶5小时到达B城。已知甲车每小时比乙车快27千米,求A、B两个城市间的公路长。
