7.1.7总复习 四则混合运算(二) 课件(39张PPT)
文档属性
| 名称 | 7.1.7总复习 四则混合运算(二) 课件(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 473.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-07 00:00:00 | ||
图片预览





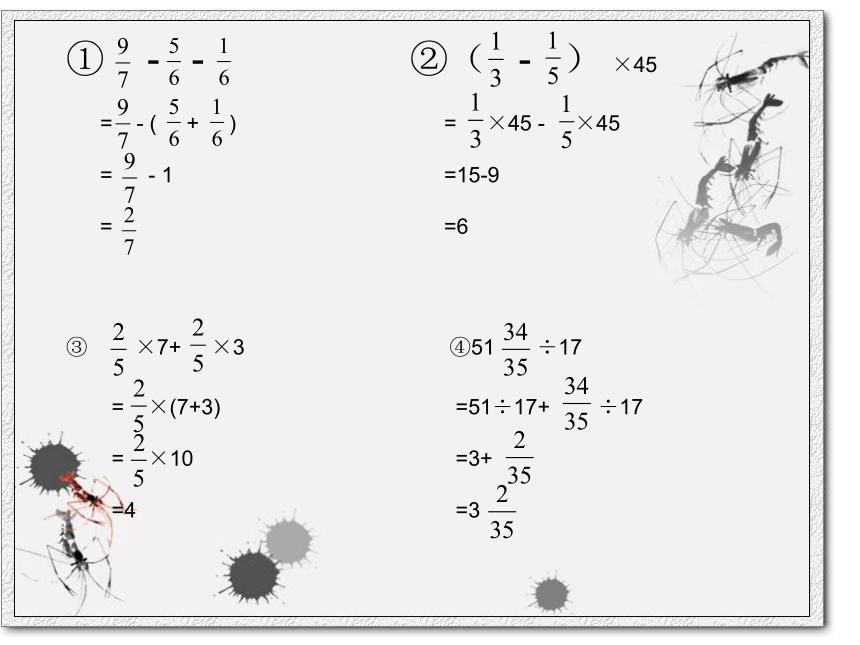
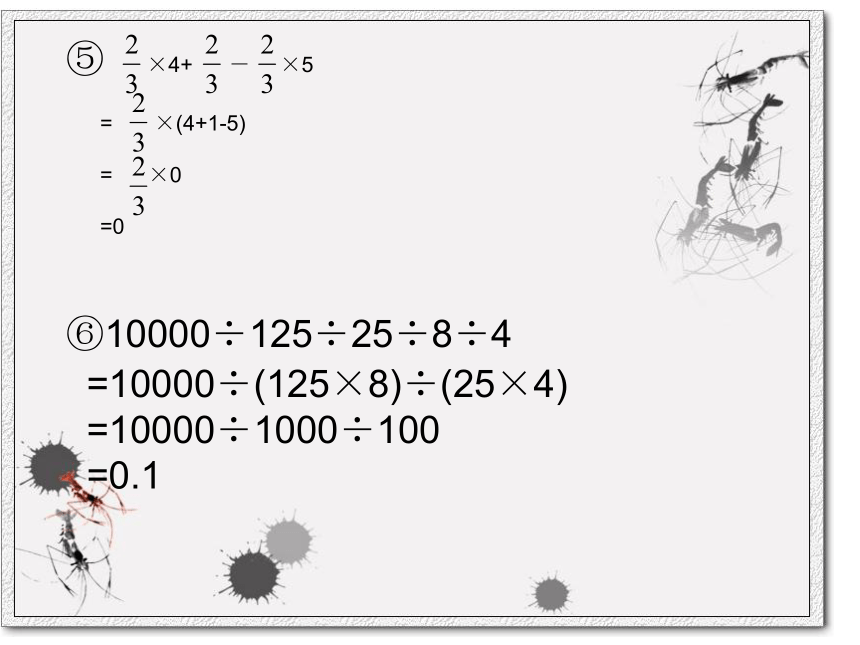



文档简介
课件39张PPT。四则混合运算一、四则运算的意义和法则
1、四则运算的意义
(1)加法的意义:把两个数合并成一个数的运算。
(2)减法的意义:已知两个加数的和与其中的一个加数,求另一个加数的运算。
(3)除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。(4)A、整数乘法的意义:求几个相同加数和的简便运算。
B、小数乘法的意义:小数乘以整数的意义与整数乘法的意义相同;一个数乘以小数,就是求这个数的十分之几、百分之几……是多少 ?
C、分数乘法的意义:分数乘以整数的意义与整数乘法的意义相同;一个数乘以分数,就是求这个数的几分之几是多少 。2、四则运算的法则
A、整数、小数
加减法:数位对齐(个位对齐或小数点对齐)
4-0.02 竖式计算
乘法:末位对齐(末尾0除外)
1.02×0.4 竖式计算 320×400
除法:除数必须化为正整数才能进行计算
0.423÷1.5=(4.23÷15) 竖式计算
B、分数(结果能约分的必须要约分--分子和分母为互质数,即化为最简分数 )
加减法:必须是同分母分数才能直接进行计算
乘法:分子乘分子,分母乘分母。
除法:乘以除数的倒数二、四则混合运算
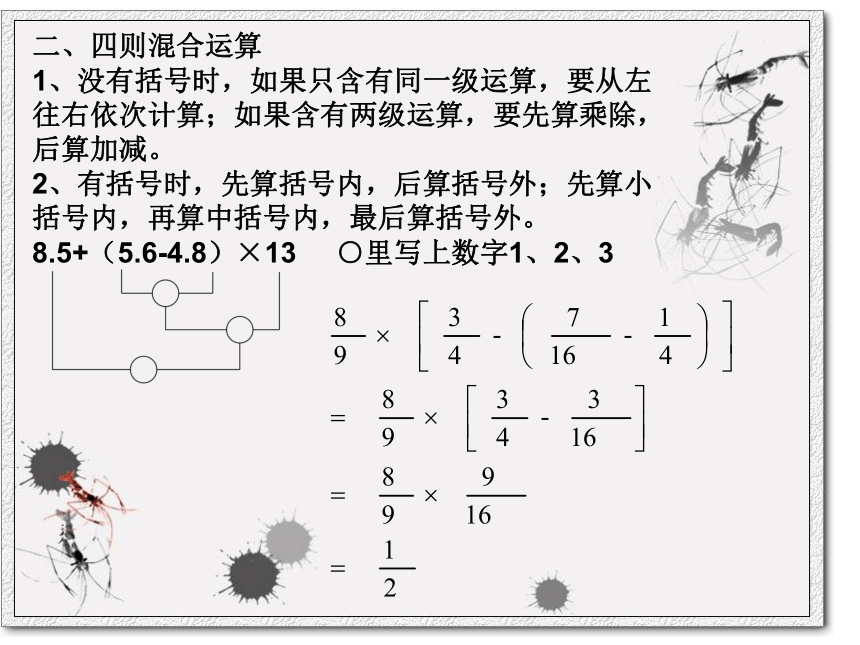
1、没有括号时,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先算乘除,后算加减。
2、有括号时,先算括号内,后算括号外;先算小括号内,再算中括号内,最后算括号外。
8.5+(5.6-4.8)×13 ○里写上数字1、2、3 三、运算定律与简便算法
加法交换律:加法结合律:乘法交换律:乘法结合律:乘法分配律:
① - - ②( - ) ×45
③ ×7+ ×3 ④51 ÷17
⑤ ×4+ - ×5
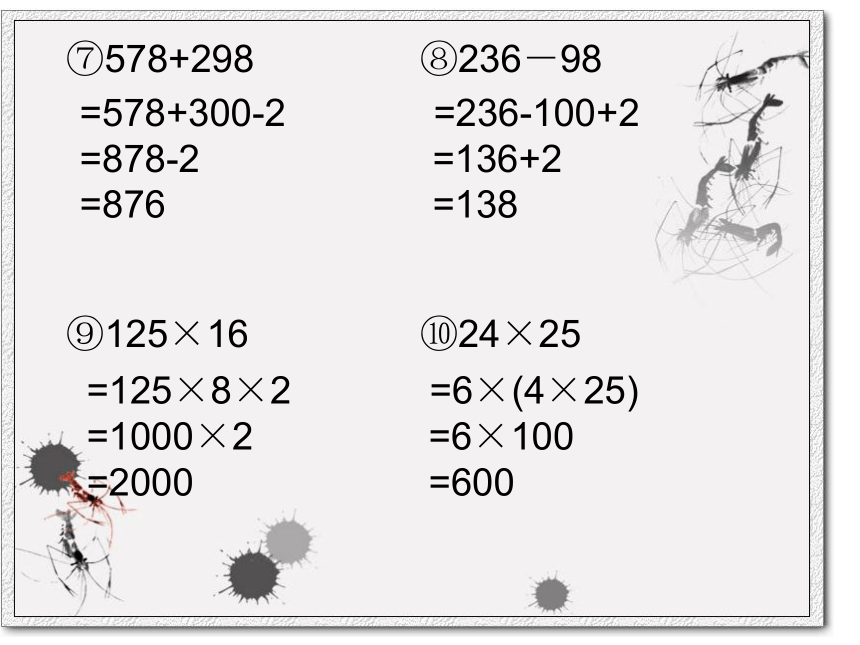
⑥10000÷125÷25÷8÷4⑦578+298 ⑧236-98
⑨125×16 ⑩24×25⑾44×25 ⑿25×(4+10)
⒀41×101 ⒁56×99⒂68%×4+0.68×5+ ⒃4×28+4×82-10÷
⒄20.07×1994-19.93×2007 ⒅72×125⒆44×25 ⒇9÷0.25
(21) × + × +2 (22)1300÷25
(23)(0.8×99+0.8)×=[0.8×(99+1)]×
=0.8×(100× )
=0.8×4
=3.2(24)2830+450÷25×4
=2830+18×4 =2830+450÷100
=2830+72 =2830+4.5
=2902 =2834.5
25、26、27、28、29、四、估算
注意:在乘法口诀范围内进行口算,以除尽为原则,答案可能不唯一
1、一个因数是一位数的乘法估算,另一个因数只保留最高位。
736×3≈700×3=2100
2、两位数除法的估算,把两位数看作整十数
632÷90≈630÷90=7 498÷72≈490÷70=7
3、估算方法
去尾法、进一法、四舍五入法、凑十法 、靠五法、平均法。
例:超市购物
果汁16.00元、火腿肠13.00元、蔬菜8.00元、洗发水23.00元、洗衣粉6.00元、牙膏3.00元,
(1)淘气估算购物的价钱一定超过40元,他的估算对吗?
去尾法:把最高位的数加起来
16+13+8+23+6+3≈10+10+20=40(元)
对
(2)妈妈带了100元,她带的钱够吗?(进一法)
16+13+8+23+6+3≈20+20+10+30+10+10=100(元 )
(3)淘气又估算了一次,他用的是什么方法?(四舍五入法)
16+13+8+23+6+3≈20+10+10+20+10+0=70(元)
假设法:全舍
4×6=24(元) 70+24=94(元)够(4)妈妈是这样估算的:凑十法
16+23≈40(元) 13+8≈20(元) 6+3≈10(元)
40+20+10=70(元)
(5)爸爸是这样估算的:凑十法
16+13≈15+15=30(元) 6+8+3≈15(元)
23≈25(元) 30+15+25=70(元 )
(6)平均法(殷浩然)
100÷6≈16(元) 23-16=7(元) 16-3=13(元)
例2:买一套《童话故事》156元和一套《成语故事》328元,大约需要多少钱?
156+328≈160+330=490(元)五、用算术法解应用题的一般步骤。
1、理解题意,明确已知条件和未知条件(所求问题)
2、分析数量关系,确定先算什么,再算什么。(确定每一步求的是什么)
3、列式计算
4、验算作答,就是检验列式过程是否合理,结果是否正确,与原题的条件是否相符,最后写出答案。六、典型分数题
(1)甲是30,乙比甲多 ,乙是多少?
(X-30)÷30=
(2)甲是30,乙比甲少 ,乙是多少?
(3)甲是30,比乙多 ,乙是多少?
(4) 甲是30,比乙少 ,乙是多少?(5)甲是30,乙是25,甲比乙多几分之几?
(6)甲是30,乙是25,乙比甲少几分之几?
(7)甲是30,乙是25,乙是甲的几分之几?
(8)甲是30,乙是甲的,甲是多少?(9)乙是25,是甲的 ,甲是多少?七、比例尺
图上距离和实际距离的比,叫做这幅图的比例尺
图上距离∶实际距离 = 比例尺注意:
(1)比例尺与一般的尺不同,它是一个比,且仅是长度比,不应带有计量单位。
(2)求比例尺时,前、后项的单位长度一定要化成同级单位.
(3)为了计算简便,比例尺的前项或后项,一般应化简成“1”.
(4)比例尺中的前项和后项不能颠倒。
(5)题中没有给出说明时,图上距离一般用厘米做单位。补充:线段比例尺是用一条标有数字的线段来表示和地面上相对应的实际距离。
(每段长度默认为1厘米长度)
0 5 10 15km
化成数值比例尺是1cm:5km=1:500000 3、代数初步
一、用字母表示数
用字母表示数可以简明地表达数量关系,运算定律和计算公式。如S=vt a+b=b+a V=Sh
注意:
不同41213二、简易方程 1、等式与方程 A、表示相等关系的式子,叫做等式。 B、含有未知数的等式,叫做方程。 2、方程的特征 A、方程必须是等式 B、方程必须含有未知数 3、方程的解和解方程 使方程左右两边相等的未知数的值,叫做方程的解。 求方程的解的过程,叫做解方程。 4、解方程的方法。 主要应用加、减、乘、除法中各部分间的关系来解方程。三、比和比例
1、比和比例的意义与性质
意义:两个数相除又叫做两个数的比。
表示两个比相等的式子叫做比例。
各部分名称:0.9 : 0.6 = 1.5
前项 后项 比值5 : 6 = 20 : 24
内项
外项基本性质:比的前项和后项都乘或除以相同的数(0除外),比值不变。在比例里,两个内项的积等于两个外项的积。(解比例)
(1)5:6=20:24 5×24=6×20
(2) 交叉相乘 5×24=6×202、正比例和反比例
正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如何判断两个数量是否成正比例关系?
反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,变化时两种量中相对应的两个数的积一定。这样两种相关联的量就叫做成反比例的量,它们之间的关系叫做反比例关系。
怎么判断两个量是不是成反比例的量呢?
① 两种量是相关联的量。
② 一种量随另一种量的扩大而减小。
③两种量变化时乘积一定,能用关系式表示为:四、找规律
1、图形的变化规律
有些图形按行列方阵的形式排列,每一行每一列都有这些图形,呈循环排列。
有些图形排成一行,每组图形呈循环排列。
◎△□□◎△□□◎△□□……
2、数列的变化规律
等差数列:每相邻两项的差是一定值。
1、3、5、7、9……
等比数列:每相邻两项的商是一定值
1、3、9、27、81……从第3个数开始,每个数都是前两项之和 1、4、5、9、14…… 每一个数都是这个数所在项数的平方 1、4、9、16、25…… 每一个数都是这个数所在项数的立方 1、8、27、64……五、数量关系式
结余=收入-支出
总产量=单产量×数量
路程=速度×时间
利息=本金×利率×时间
工作总量=工效×时间注:工效是指单位时间内的工作量。
例:某个工人8天生产了160个零件,他每天能生产多少个零件?(他的工作效率是多少?)
解1:160÷8=20(个)
解2:1÷8=答:每天能生产20个零件;每天能生产
收入、单价、路程……叫做数量名称例:打一份3000字的稿件。小明要10分钟才能完成,小李要15分钟才能完成,如果两人同时打这份稿件,至少要多少分钟才能完成?
解1:3000÷10=300(字)3000÷15=200(字)
3000÷(300+200)=6(分)
解2:六、找单位“1”
1、找关键字,确定单位“1”(单位“1”表示标准量)
A、“的”前面是单位“1”
B、“是、比、占、相当于”后面是单位“1”
2、找总量确定单位“1”
没有关键字时,哪个量表示总数,就以哪个量为单位“1”
3、原数量与现数量
原数量是单位“1”
例:(1)水结成冰后,体积增加了几分之几?
水是原数量,所以水是单位“1”
(2)冰融化成水,体积减少了几分之几?
冰是原数量,所以冰是单位“1”4、找不变量,确定单位“1”(单位“1”的转化)
找一下不变量,以这个不变量为单位“1”
例:五(2)男生人数占全班人数的 , 转走8名男生后,男生人数占全班人数的 ,原来全班有多少人?
分析:男生(变量),女生(不变量),总人数(变量),所以以女生(不变量)为单位“1”
转走前:女生: 男生占女生:转走后:女生: 男生占女生:女生:全班:找等量关系式:以题中的某一个量列等式。
题中一共有3个量:总人数、男生人数、女生人数。其中总人数设为
,只能以男生人数或女生人数列等量关系式。
方程解:
解:设原来全班有χ人?
以男生人数列等式为:方程解:
解:设原来全班有χ人?
以女生人数列等式为:
1、没有括号时,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先算乘除,后算加减。
2、有括号时,先算括号内,后算括号外;先算小括号内,再算中括号内,最后算括号外。
8.5+(5.6-4.8)×13 ○里写上数字1、2、3 三、运算定律与简便算法
加法交换律:加法结合律:乘法交换律:乘法结合律:乘法分配律:
① - - ②( - ) ×45
③ ×7+ ×3 ④51 ÷17
⑤ ×4+ - ×5
⑥10000÷125÷25÷8÷4⑦578+298 ⑧236-98
⑨125×16 ⑩24×25⑾44×25 ⑿25×(4+10)
⒀41×101 ⒁56×99⒂68%×4+0.68×5+ ⒃4×28+4×82-10÷
⒄20.07×1994-19.93×2007 ⒅72×125⒆44×25 ⒇9÷0.25
(21) × + × +2 (22)1300÷25
(23)(0.8×99+0.8)×=[0.8×(99+1)]×
=0.8×(100× )
=0.8×4
=3.2(24)2830+450÷25×4
=2830+18×4 =2830+450÷100
=2830+72 =2830+4.5
=2902 =2834.5
25、26、27、28、29、四、估算
注意:在乘法口诀范围内进行口算,以除尽为原则,答案可能不唯一
1、一个因数是一位数的乘法估算,另一个因数只保留最高位。
736×3≈700×3=2100
2、两位数除法的估算,把两位数看作整十数
632÷90≈630÷90=7 498÷72≈490÷70=7
3、估算方法
去尾法、进一法、四舍五入法、凑十法 、靠五法、平均法。
例:超市购物
果汁16.00元、火腿肠13.00元、蔬菜8.00元、洗发水23.00元、洗衣粉6.00元、牙膏3.00元,
(1)淘气估算购物的价钱一定超过40元,他的估算对吗?
去尾法:把最高位的数加起来
16+13+8+23+6+3≈10+10+20=40(元)
对
(2)妈妈带了100元,她带的钱够吗?(进一法)
16+13+8+23+6+3≈20+20+10+30+10+10=100(元 )
(3)淘气又估算了一次,他用的是什么方法?(四舍五入法)
16+13+8+23+6+3≈20+10+10+20+10+0=70(元)
假设法:全舍
4×6=24(元) 70+24=94(元)够(4)妈妈是这样估算的:凑十法
16+23≈40(元) 13+8≈20(元) 6+3≈10(元)
40+20+10=70(元)
(5)爸爸是这样估算的:凑十法
16+13≈15+15=30(元) 6+8+3≈15(元)
23≈25(元) 30+15+25=70(元 )
(6)平均法(殷浩然)
100÷6≈16(元) 23-16=7(元) 16-3=13(元)
例2:买一套《童话故事》156元和一套《成语故事》328元,大约需要多少钱?
156+328≈160+330=490(元)五、用算术法解应用题的一般步骤。
1、理解题意,明确已知条件和未知条件(所求问题)
2、分析数量关系,确定先算什么,再算什么。(确定每一步求的是什么)
3、列式计算
4、验算作答,就是检验列式过程是否合理,结果是否正确,与原题的条件是否相符,最后写出答案。六、典型分数题
(1)甲是30,乙比甲多 ,乙是多少?
(X-30)÷30=
(2)甲是30,乙比甲少 ,乙是多少?
(3)甲是30,比乙多 ,乙是多少?
(4) 甲是30,比乙少 ,乙是多少?(5)甲是30,乙是25,甲比乙多几分之几?
(6)甲是30,乙是25,乙比甲少几分之几?
(7)甲是30,乙是25,乙是甲的几分之几?
(8)甲是30,乙是甲的,甲是多少?(9)乙是25,是甲的 ,甲是多少?七、比例尺
图上距离和实际距离的比,叫做这幅图的比例尺
图上距离∶实际距离 = 比例尺注意:
(1)比例尺与一般的尺不同,它是一个比,且仅是长度比,不应带有计量单位。
(2)求比例尺时,前、后项的单位长度一定要化成同级单位.
(3)为了计算简便,比例尺的前项或后项,一般应化简成“1”.
(4)比例尺中的前项和后项不能颠倒。
(5)题中没有给出说明时,图上距离一般用厘米做单位。补充:线段比例尺是用一条标有数字的线段来表示和地面上相对应的实际距离。
(每段长度默认为1厘米长度)
0 5 10 15km
化成数值比例尺是1cm:5km=1:500000 3、代数初步
一、用字母表示数
用字母表示数可以简明地表达数量关系,运算定律和计算公式。如S=vt a+b=b+a V=Sh
注意:
不同41213二、简易方程 1、等式与方程 A、表示相等关系的式子,叫做等式。 B、含有未知数的等式,叫做方程。 2、方程的特征 A、方程必须是等式 B、方程必须含有未知数 3、方程的解和解方程 使方程左右两边相等的未知数的值,叫做方程的解。 求方程的解的过程,叫做解方程。 4、解方程的方法。 主要应用加、减、乘、除法中各部分间的关系来解方程。三、比和比例
1、比和比例的意义与性质
意义:两个数相除又叫做两个数的比。
表示两个比相等的式子叫做比例。
各部分名称:0.9 : 0.6 = 1.5
前项 后项 比值5 : 6 = 20 : 24
内项
外项基本性质:比的前项和后项都乘或除以相同的数(0除外),比值不变。在比例里,两个内项的积等于两个外项的积。(解比例)
(1)5:6=20:24 5×24=6×20
(2) 交叉相乘 5×24=6×202、正比例和反比例
正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如何判断两个数量是否成正比例关系?
反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,变化时两种量中相对应的两个数的积一定。这样两种相关联的量就叫做成反比例的量,它们之间的关系叫做反比例关系。
怎么判断两个量是不是成反比例的量呢?
① 两种量是相关联的量。
② 一种量随另一种量的扩大而减小。
③两种量变化时乘积一定,能用关系式表示为:四、找规律
1、图形的变化规律
有些图形按行列方阵的形式排列,每一行每一列都有这些图形,呈循环排列。
有些图形排成一行,每组图形呈循环排列。
◎△□□◎△□□◎△□□……
2、数列的变化规律
等差数列:每相邻两项的差是一定值。
1、3、5、7、9……
等比数列:每相邻两项的商是一定值
1、3、9、27、81……从第3个数开始,每个数都是前两项之和 1、4、5、9、14…… 每一个数都是这个数所在项数的平方 1、4、9、16、25…… 每一个数都是这个数所在项数的立方 1、8、27、64……五、数量关系式
结余=收入-支出
总产量=单产量×数量
路程=速度×时间
利息=本金×利率×时间
工作总量=工效×时间注:工效是指单位时间内的工作量。
例:某个工人8天生产了160个零件,他每天能生产多少个零件?(他的工作效率是多少?)
解1:160÷8=20(个)
解2:1÷8=答:每天能生产20个零件;每天能生产
收入、单价、路程……叫做数量名称例:打一份3000字的稿件。小明要10分钟才能完成,小李要15分钟才能完成,如果两人同时打这份稿件,至少要多少分钟才能完成?
解1:3000÷10=300(字)3000÷15=200(字)
3000÷(300+200)=6(分)
解2:六、找单位“1”
1、找关键字,确定单位“1”(单位“1”表示标准量)
A、“的”前面是单位“1”
B、“是、比、占、相当于”后面是单位“1”
2、找总量确定单位“1”
没有关键字时,哪个量表示总数,就以哪个量为单位“1”
3、原数量与现数量
原数量是单位“1”
例:(1)水结成冰后,体积增加了几分之几?
水是原数量,所以水是单位“1”
(2)冰融化成水,体积减少了几分之几?
冰是原数量,所以冰是单位“1”4、找不变量,确定单位“1”(单位“1”的转化)
找一下不变量,以这个不变量为单位“1”
例:五(2)男生人数占全班人数的 , 转走8名男生后,男生人数占全班人数的 ,原来全班有多少人?
分析:男生(变量),女生(不变量),总人数(变量),所以以女生(不变量)为单位“1”
转走前:女生: 男生占女生:转走后:女生: 男生占女生:女生:全班:找等量关系式:以题中的某一个量列等式。
题中一共有3个量:总人数、男生人数、女生人数。其中总人数设为
,只能以男生人数或女生人数列等量关系式。
方程解:
解:设原来全班有χ人?
以男生人数列等式为:方程解:
解:设原来全班有χ人?
以女生人数列等式为:
