【2019年高考理科数学三轮冲刺直线与圆 教案
文档属性
| 名称 | 【2019年高考理科数学三轮冲刺直线与圆 教案 | 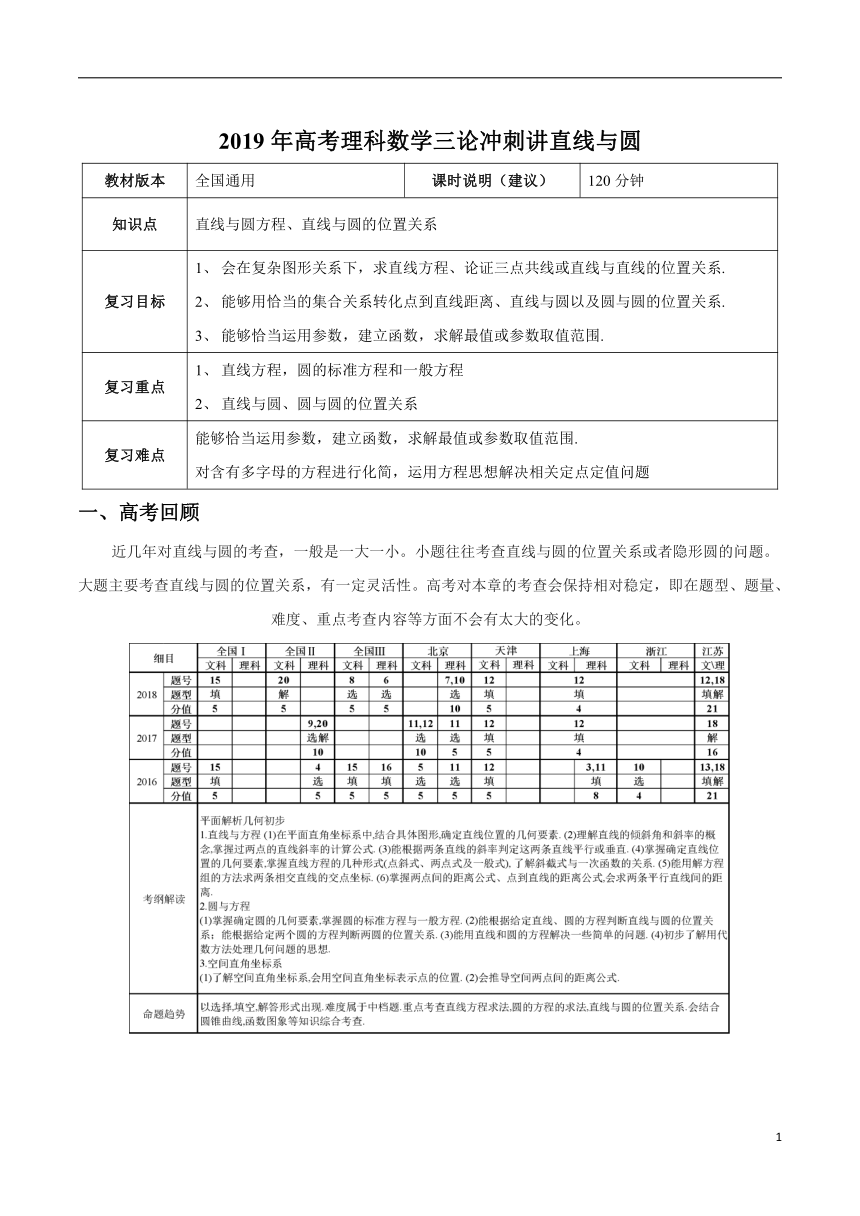 | |
| 格式 | zip | ||
| 文件大小 | 553.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 17:13:04 | ||
图片预览




文档简介
2019年高考理科数学三论冲刺讲直线与圆
教材版本 全国通用 课时说明(建议) 120分钟
知识点 直线与圆方程、直线与圆的位置关系
复习目标 会在复杂图形关系下,求直线方程、论证三点共线或直线与直线的位置关系. 能够用恰当的集合关系转化点到直线距离、直线与圆以及圆与圆的位置关系. 能够恰当运用参数,建立函数,求解最值或参数取值范围.
复习重点 直线方程,圆的标准方程和一般方程 直线与圆、圆与圆的位置关系
复习难点 能够恰当运用参数,建立函数,求解最值或参数取值范围. 对含有多字母的方程进行化简,运用方程思想解决相关定点定值问题
一、高考回顾
近几年对直线与圆的考查,一般是一大一小。小题往往考查直线与圆的位置关系或者隐形圆的问题。大题主要考查直线与圆的位置关系,有一定灵活性。高考对本章的考查会保持相对稳定,即在题型、题量、难度、重点考查内容等方面不会有太大的变化。
二、知识清单
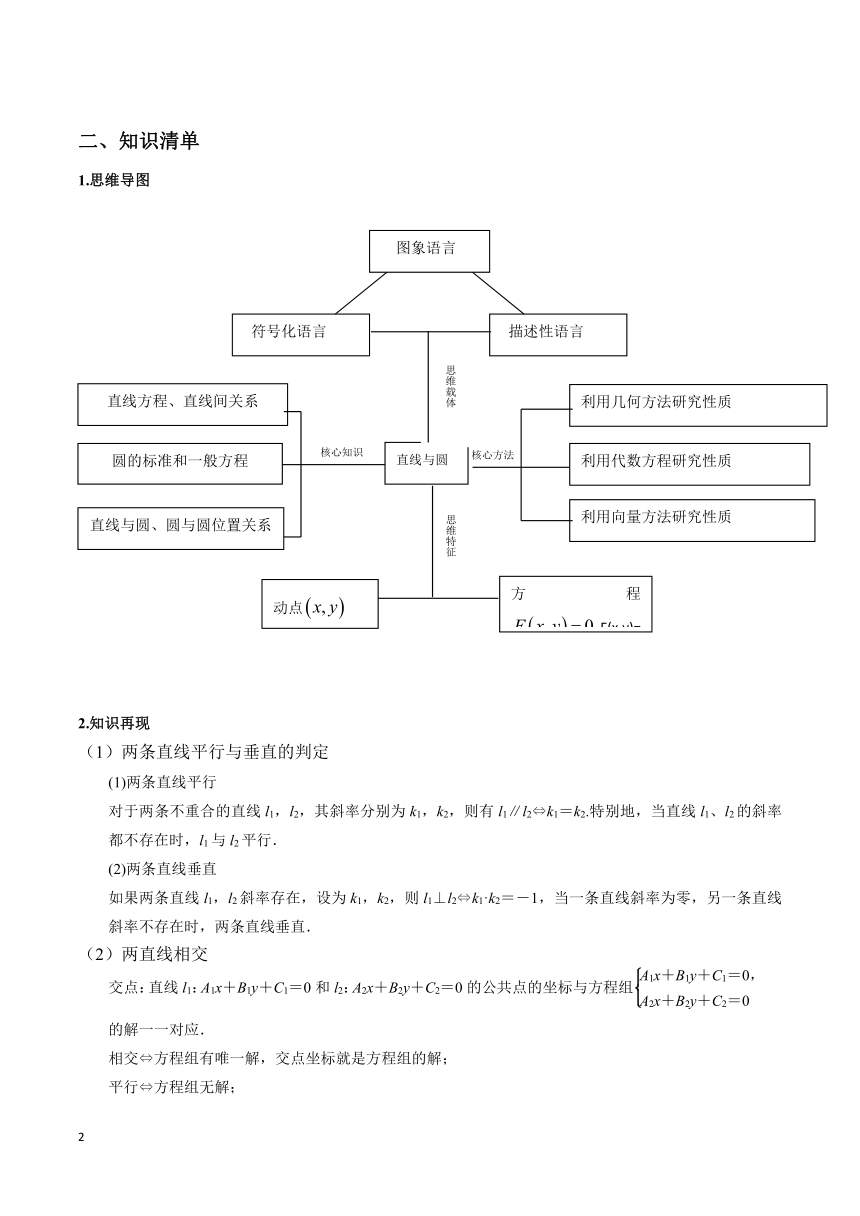
1.思维导图
(
核心方法
思维特征
动点
方程
F(x,y)=0
直线方程、直线间关系
圆的标准和一般方程
直线与圆、圆与圆位置关系
核心知识
直线与圆
利用几何方法研究性质
利用代数方程研究性质
利用向量方法研究性质
图象语言
符号化语言
描述性语言
思维载体
)
2.知识再现
(1)两条直线平行与垂直的判定
(1)两条直线平行
对于两条不重合的直线l1,l2,其斜率分别为k1,k2,则有l1∥l2?k1=k2.特别地,当直线l1、l2的斜率都不存在时,l1与l2平行.
(2)两条直线垂直
如果两条直线l1,l2斜率存在,设为k1,k2,则l1⊥l2?k1·k2=-1,当一条直线斜率为零,另一条直线斜率不存在时,两条直线垂直.
(2)两直线相交
交点:直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的公共点的坐标与方程组的解一一对应.
相交?方程组有唯一解,交点坐标就是方程组的解;
平行?方程组无解;
重合?方程组有无数个解.
(3)三种距离公式
点A(x1,y1)、B(x2,y2)间的距离:AB=.
点P(x0,y0)到直线l:Ax+By+C=0的距离:d=.
两平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0 (C1≠C2)间的距离为d=.
(4)圆的标准方程
(x-a)2+(y-b)2=r2(r>0),其中(a,b)为圆心,r为半径.
(5)圆的一般方程
x2+y2+Dx+Ey+F=0表示圆的充要条件是D2+E2-4F>0,其中圆心为,半径r=.
(6)确定圆的方程的方法和步骤
确定圆的方程主要方法是待定系数法,大致步骤为
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于a,b,r或D、E、F的方程组;
(3)解出a、b、r或D、E、F代入标准方程或一般方程.
(7)点与圆的位置关系
点和圆的位置关系有三种.
圆的标准方程(x-a)2+(y-b)2=r2,点M(x0,y0)
(1)点在圆上:(x0-a)2+(y0-b)2=r2;
(2)点在圆外:(x0-a)2+(y0-b)2>r2;
(3)点在圆内:(x0-a)2+(y0-b)2(8)直线与圆的位置关系
1.位置关系有三种:相离、相切、相交.
2.判断直线与圆的位置关系常见的有两种方法:
①代数法:利用判别式Δ,即直线方程与圆的方程联立方程组消去或整理成一元二次方程后,计算判别式Δ
②几何法:利用圆心到直线的距离d和圆半径r的大小关系:
(9)圆的切线方程
1.若圆的方程为,点在圆上,则过点且与圆相切的切线方程为.
注:点必须在圆上.
2.经过圆上点的切线方程为:
.
(10)计算直线被圆截得的弦长的常用方法
①几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
②代数方法
运用韦达定理及弦长公式
说明:圆的弦长、弦心距的计算常用几何方法.
(11)圆与圆的位置关系
1.圆与圆的位置关系可分为五种:相离、相交、外切、内切、内含.
2.判断圆与圆的位置关系常用方法:
(几何法)设两圆圆心分别为、,半径为、,当相离;外切;相交;内切;内含.
3.已知两圆和相交,则与两圆共交点的圆系方程为,其中为的任意常数,因此圆系不包括第二个圆.
4.当时,为两圆公共弦所在的直线,方程为.
三、例题精讲
题型一直线方程、两直线的位置关系
例1已知两直线和.试确定、的值,使:
(1)与相交于点;
(2)∥;
(3)⊥,且在轴上的截距为-1.
【答案】(1),.
(2),时或,时,∥.
(3),
【解析】(1)由题意得,解得,.
(2)当时,显然不平行于;
当时,由,得 或.
即,时或,时,∥.
(3)当且仅当,即时,⊥.又,∴.
即,时,⊥,且在轴上的截距为-1.
【易错点】忽略对的情况的讨论
【思维点拨】遇到直线类题型,首先要注意特殊情况如斜率不存在时或时,并且对于直线平行和垂直时与和间的关系要熟练记忆。
例2如图,设一直线过点(-1,1),它被两平行直线l1:x+2y-1=0,l2:x+2y-3=0所截的线段的中点在直线l3:x-y-1=0上,求其方程.
【答案】.
【解析】与、平行且距离相等的直线方程为.
设所求直线方程为,即.又直线过,∴.解.∴所求直线方程为.
【易错点】求错与、平行且距离相等的直线方程
【思维点拨】本题的关键在于求到、平行且距离相等的直线方程,再利用这条直线求出和第三条支线的交点,从而求解本题.
题型二 圆的方程(对称问题、圆的几何性质运用)
例1已知实数、满足方程.
(1)求的最大值和最小值;
(2)求的最大值和最小值.
【答案】(1)的最大值为,最小值为.
(2)的最大值为,最小值为.
【解析】(1)原方程化为,表示以点为圆心,以为半径的圆.设,即,当直线与圆相切时,斜率取最大值和最小值,此时,解得.故的最大值为,最小值为.
(2)设,即,当与圆相切时,纵截距取得最大值和最小值,此时,即.故的最大值为,最小值为.
【易错点】理解错给定要求结果的含义
【思维点拨】正确理解给定结果的含义,在利用题中的条件解决问题。
例2已知点,为圆上一动点,当点在圆上运动时,的中点的轨迹方程是 .
【答案】.
【解析】设点为所求轨迹上任意一点,.
因为M为PQ的中点,所以即
又因为点在圆上,
所以,
故所求的轨迹方程为.
【易错点】中点的错误应用
【思维点拨】求出中点横纵坐标的方程及求出所求的直线
题型三 直线与圆、圆与圆的位置关系
例1在平面直角坐标系xOy中,已知圆C:x2+(y-3)2=2,点A是x轴上的一个动点,AP,AQ分别切圆C于P,Q两点,则线段PQ长的取值范围是 .
【答案】PQ∈.
【解析】设∠PCA=θ,所以PQ=2sin θ.
又cos θ=,AC∈[3,+∞),所以cos θ∈,
所以cos2θ∈,sin2θ=1-cos2θ∈,
所以sin θ∈,所以PQ∈.
【易错点】直接去求线段的长度
【思维点拨】转化思想,把要求的线段长度转化为角度的关系,从而解决问题.
例2已知圆
(1)若圆的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆外一点向该圆引一条切线,切点为为坐标原点,且有求使得取得最小值时点的坐标.
【答案】(1),或.
(2)
【解析】(1)将圆配方得.
当直线在两坐标轴上的截距为零时,设直线方程为 ,
由,解得,得.
当直线在两坐标轴上的截距不为零时,
设直线方程为,由,得,.
∴直线方程为,或.
(2)由,得,
即点在直线上.
当取最小值时,即取得最小值,直线,
∴直线的方程为.
得点的坐标为.
【易错点】没有分类讨论
【思维点拨】考查用点斜式、斜截式求直线的方法,利用分类讨论思想来解决问题
题型四 定点定值轨迹问题
例1已知t∈R,圆C:x2+y2-2tx-2t2y+4t-4=0.
(1)若圆C的圆心在直线x-y+2=0上,求圆C的方程.
(2)圆C是否过定点?如果过定点,求出定点的坐标;如果不过定点,请说明理由.
【答案】(1)圆C的方程为x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0.
(2)过定点,定点坐标为
【解析】(1)由原方程配方得(x-t)2+(y-t2)2=t4+t2-4t+4,其圆心为C(t,t2).
依题意知t-t2+2=0,所以t=-1或2.
即圆C的方程为x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0.
(2)整理圆C的方程为(x2+y2-4)+(-2x+4)t+(-2y)·t2=0,
令
所以圆C过定点(2,0).
【易错点】漏解
【思维点拨】判定圆是否过定点,或是求圆所过定点坐标的问题,可以在方程形式上转化为关于某个参量的方程,结合恒等式的关系,再构造关于x,y的方程组求该点的坐标.若方程组有解,则说明圆过定点,否则圆不过定点.
例2如图,已知圆C:x2+(y-3)2=4,一动直线l过点A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N.
(1)求证:当l与m垂直时,l必过圆心C.
(2)当PQ=2时,求直线l的方程.
(3)探索·是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
【答案】(1)见解析
(2)x=-1或4x-3y+4=0.
(3)·与直线l的倾斜角无关,且·=-5.
【解析】(1)因为l与m垂直,且km=-,所以kl=3.又kAC=3,所以当l与m垂直时,l的方程为y=3(x+1),l必过圆心C.
(2)①当直线l与x轴垂直时,易知x=-1,符合题意.
②当直线l与x轴不垂直时,
设直线l的方程为y=k(x+1),即kx-y+k=0.
因为PQ=2 ,所以CM==1,
则由CM==1,得k=,
所以直线l:4x-3y+4=0,
从而所求的直线l的方程为x=-1或4x-3y+4=0.
因为CM⊥MN,所以
·=(+)·=·+·=·.
①当l与x轴垂直时,易得N,
则=.又=(1,3),
所以·=·=-5;
②当l的斜率存在时,设直线l的方程为y=k(x+1),
则由得N,
则=,
所以·=·=+=-5.
综上,·与直线l的倾斜角无关,且·=-5.
【易错点】忽略对斜率不存在情况的讨论
【思维点拨】一般地,涉及到圆的切线或考虑其弦长问题时,若需要求直线的方程,则务必要全面考虑问题,即要考虑直线的斜率存在与不存在两种情况.
四、成果巩固
题型一直线方程、两直线的位置关系
1.已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
【答案】(1)当a=-1时,l1∥l2,否则l1与l2不平行
(2)a=
【解析】(1)由A1B2-A2B1=0,得a(a-1)-1×2=0,由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,
∴l1∥l2?,
故当a=-1时,l1∥l2,否则l1与l2不平行.
(2) 由A1A2+B1B2=0得a+2(a-1)=0?a=.
2.已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0,在坐标平面内求一点P,使PA=PB,且点P到直线l的距离为2.
【答案】P的坐标为或
【解析】设点P的坐标为(a,b),∵A(4,-3),B(2,-1),
∴线段AB的中点M的坐标为(3,-2),
∴线段AB的垂直平分线方程为y+2=x-3,即x-y-5=0.
∵点P(a,b)在上述直线上,∴a-b-5=0.①
又P(a,b)到直线l:4x+3y-2=0的距离为2,∴=2,即4a+3b-2=±10,②
联立①②可得或.∴所求点P的坐标为或.
3.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是________.
【答案】CD=2
【解析】由题意知点P关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),则光线所经过的路程PMN的长为CD=2.
题型二 圆的方程(对称问题、圆的几何性质运用)
1.根据下列条件,求圆的方程:
(1)经过P(-2,4)、Q(3,-1)两点,并且在x轴上截得的弦长等于6;
(2)圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2).
【答案】(1)x2+y2-2x-4y-8=0,或x2+y2-6x-8y=0
(2)(x-1)2+(y+4)2=8
【解析】(1)设圆的方程为x2+y2+Dx+Ey+F=0,
将P、Q点的坐标分别代入得
又令y=0,得x2+Dx+F=0.③
设x1,x2是方程③的两根,由|x1-x2|=6有D2-4F=36,④
由①、②、④解得D=-2,E=-4,F=-8,或D=-6,E=-8,F=0.
故所求圆的方程为x2+y2-2x-4y-8=0,或x2+y2-6x-8y=0.
(2) 如图,设圆心(x0,-4x0),依题意得=1,
∴x0=1,即圆心坐标为(1,-4),半径r=2,
故圆的方程为(x-1)2+(y+4)2=8.
2.在平面直角坐标系xOy中,二次函数f(x)=x2+2x+b(x∈R)与两坐标轴有三个交点.记过三个交点的圆为圆C.
(1)求圆C的方程;
(2)圆C是否经过定点(与b的取值无关)?证明你的结论.
【答案】(1)x2+y2+2x-(b+1)y+b=0.
(2)圆C必过定点(0,1),(-2,1)
【解析】(1)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,令y=0,得x2+Dx+F=0,这与x2+2x+b=0是同一个方程,故D=2,F=b;令x=0,得y2+Ey+b=0,此方程有一个根为b,代入得E=-b-1,所以圆C的方程为x2+y2+2x-(b+1)y+b=0.
(2)圆C必过定点(0,1),(-2,1).
证明如下:原方程转化为(x2+y2+2x-y)+b(1-y)=0,即解得或.
3.点P(4,-2)与圆x2+y2=4上任一点连线的中点轨迹方程是___________.
【答案】(x-2)2+(y+1)2=1
【解析】设圆上任一点坐标为(x0,y0),x+y=4,连线中点坐标为(x,y),
则?,代入x+y=4中得(x-2)2+(y+1)2=1.
题型三 直线与圆、圆与圆的位置关系
1.若过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤4}分为两部分,且使得这两部分的面积之差最大,则该直线的方程为 .
【答案】x+y-2=0
【解析】当圆心与点P的连线和过点P的直线垂直时,符合条件.圆心O与点P连线的斜率k=1,所以所求直线的斜率为-1,故所求直线方程为x+y-2=0.
2. 直线与圆相交于两点,若,则的取值范围是________.
【答案】
【解析】
设圆心为,弦的中点为,当时,
.∴当时,圆心到直线的距离.∴.∴,∴
3.若圆O:x2+y2=5与圆O1:(x-m)2+y2=20(m∈R)相交于A,B两点,且两圆在点A处的切线互相垂直,则线段AB的长是 .
【答案】
【解析】依题意得OO1==5,且△OO1A是直角三角形,=··OO1=·OA·AO1,因此AB===4.
题型四 定点定值轨迹问题
1. 如图,在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.设动圆C同时平分圆C1、圆C2的周长.
(1)求证:动圆圆心C在一条定直线上运动.
(2)动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
【答案】(1)动圆圆心C在定直线x+y-3=0上运动
(2)动圆C过定点,定点的坐标为和.
【解析】(1)设圆心C(x,y),由题意,得CC1=CC2,
即=,
化简得x+y-3=0,
即动圆圆心C在定直线x+y-3=0上运动.
(2)圆C过定点.
设C(m,3-m),则动圆C的半径为
=.
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理,得x2+y2-6y-2-2m(x-y+1)=0,
联立方程组
解得或
所以动圆C过定点,定点的坐标为和.
2. 已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆相切,求直线l1的方程.
(2)若l1与圆相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM·AN是否为定值?若是,则求出定值;若不是,请说明理由.
【答案】(1)x=1或3x-4y-3=0.
(2)AM·AN是定值且为6.
【解析】(1)①若直线l1的斜率不存在,即直线为x=1,符合题意.
②若直线l1斜率存在,设直线l1的方程为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即=2,解得k=,
所以所求直线方程为x=1或3x-4y-3=0.
(2)方法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0.
由得N.
又因为直线CM与l1垂直,
由得M,
所以AM·AN=·
=·=6为定值.故AM·AN是定值且为6.
方法二:直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0.
由得N.
再由
得(1+k2)x2-(2k2+8k+6)x+k2+8k+21=0,
所以x1+x2=,得M.
以下同方法一.
方法三:(几何法)
(变式)
连接CA并延长交l2于点B,由题知kAC=2,=-,
所以CB⊥l2.
如图,△AMC∽△ABN,
所以=,
可得AM·AN=AC·AB=2·=6,是定值.
3. 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
【答案】(1)y=3或3x+4y-12=0.
(2)
【解析】(1)由得圆心C为(3,2),
因为圆C的半径为1,
所以圆C的方程为(x-3)2+(y-2)2=1.
由题知切线的斜率一定存在,
设所求圆C的切线方程为y=kx+3,即kx-y+3=0,
所以=1,所以|3k+1|=,
所以2k(4k+3)=0,所以k=0或k=-.
所以所求圆C的切线方程为y=3或y=-x+3,
即y=3或3x+4y-12=0.
(2)因为圆C的圆心在直线l:y=2x-4上,
所以设圆心C为(a,2a-4),
则圆C的方程为(x-a)2+[y-(2a-4)]2=1.
又因为MA=2MO,所以设点M(x,y),
则=2,整理得
x2+(y+1)2=4,设为圆D.
所以点M应该既在圆C上又在圆D上,即圆C和圆D有交点,所以|2-1|≤≤|2+1|,
由5a2-12a+8≥0得a∈R;
由5a2-12a≤0,得0≤a≤.
终上所述,实数a的取值范围为
五、课堂小结
1.有关直线的题目要注意对斜率存在与否进行讨论,直线的五种表达形式各有优缺点要随题意而定。
2.与圆有关的最值和范围的讨论常用以下方法:
(1)结合圆的方程的特点确定几何量之间的大小关系;
(2)函数值域求解法,即把所讨论的参数作为一个函数,一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的取值范围;
(3)利用不等式,若能将问题能转化为“和为定值”或“积为定值”,则可以用基本不等式求解.
3.定点问题的求解步骤:
(1)选参变量:需要证明过定点的动直线(曲线)往往随着某一个量的变化而变化,可以选择这个量为参变量(当涉及到的参变量较多时,也可以选择多个参变量);
(2)求动直线(曲线)方程:求出只含上述参变量的动直线(曲线)方程,并由其他条件减少参变量的个数,最终使方程中只含一个参变量;
(3)定点:求出定点坐标.不妨设方程中所含参变量为λ,把方程写为形如f(x,y)+λg(x,y)=0的形式,然后解关于x,y的方程组得到定点坐标.
2
1
教材版本 全国通用 课时说明(建议) 120分钟
知识点 直线与圆方程、直线与圆的位置关系
复习目标 会在复杂图形关系下,求直线方程、论证三点共线或直线与直线的位置关系. 能够用恰当的集合关系转化点到直线距离、直线与圆以及圆与圆的位置关系. 能够恰当运用参数,建立函数,求解最值或参数取值范围.
复习重点 直线方程,圆的标准方程和一般方程 直线与圆、圆与圆的位置关系
复习难点 能够恰当运用参数,建立函数,求解最值或参数取值范围. 对含有多字母的方程进行化简,运用方程思想解决相关定点定值问题
一、高考回顾
近几年对直线与圆的考查,一般是一大一小。小题往往考查直线与圆的位置关系或者隐形圆的问题。大题主要考查直线与圆的位置关系,有一定灵活性。高考对本章的考查会保持相对稳定,即在题型、题量、难度、重点考查内容等方面不会有太大的变化。
二、知识清单
1.思维导图
(
核心方法
思维特征
动点
方程
F(x,y)=0
直线方程、直线间关系
圆的标准和一般方程
直线与圆、圆与圆位置关系
核心知识
直线与圆
利用几何方法研究性质
利用代数方程研究性质
利用向量方法研究性质
图象语言
符号化语言
描述性语言
思维载体
)
2.知识再现
(1)两条直线平行与垂直的判定
(1)两条直线平行
对于两条不重合的直线l1,l2,其斜率分别为k1,k2,则有l1∥l2?k1=k2.特别地,当直线l1、l2的斜率都不存在时,l1与l2平行.
(2)两条直线垂直
如果两条直线l1,l2斜率存在,设为k1,k2,则l1⊥l2?k1·k2=-1,当一条直线斜率为零,另一条直线斜率不存在时,两条直线垂直.
(2)两直线相交
交点:直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的公共点的坐标与方程组的解一一对应.
相交?方程组有唯一解,交点坐标就是方程组的解;
平行?方程组无解;
重合?方程组有无数个解.
(3)三种距离公式
点A(x1,y1)、B(x2,y2)间的距离:AB=.
点P(x0,y0)到直线l:Ax+By+C=0的距离:d=.
两平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0 (C1≠C2)间的距离为d=.
(4)圆的标准方程
(x-a)2+(y-b)2=r2(r>0),其中(a,b)为圆心,r为半径.
(5)圆的一般方程
x2+y2+Dx+Ey+F=0表示圆的充要条件是D2+E2-4F>0,其中圆心为,半径r=.
(6)确定圆的方程的方法和步骤
确定圆的方程主要方法是待定系数法,大致步骤为
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于a,b,r或D、E、F的方程组;
(3)解出a、b、r或D、E、F代入标准方程或一般方程.
(7)点与圆的位置关系
点和圆的位置关系有三种.
圆的标准方程(x-a)2+(y-b)2=r2,点M(x0,y0)
(1)点在圆上:(x0-a)2+(y0-b)2=r2;
(2)点在圆外:(x0-a)2+(y0-b)2>r2;
(3)点在圆内:(x0-a)2+(y0-b)2
1.位置关系有三种:相离、相切、相交.
2.判断直线与圆的位置关系常见的有两种方法:
①代数法:利用判别式Δ,即直线方程与圆的方程联立方程组消去或整理成一元二次方程后,计算判别式Δ
②几何法:利用圆心到直线的距离d和圆半径r的大小关系:
(9)圆的切线方程
1.若圆的方程为,点在圆上,则过点且与圆相切的切线方程为.
注:点必须在圆上.
2.经过圆上点的切线方程为:
.
(10)计算直线被圆截得的弦长的常用方法
①几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
②代数方法
运用韦达定理及弦长公式
说明:圆的弦长、弦心距的计算常用几何方法.
(11)圆与圆的位置关系
1.圆与圆的位置关系可分为五种:相离、相交、外切、内切、内含.
2.判断圆与圆的位置关系常用方法:
(几何法)设两圆圆心分别为、,半径为、,当相离;外切;相交;内切;内含.
3.已知两圆和相交,则与两圆共交点的圆系方程为,其中为的任意常数,因此圆系不包括第二个圆.
4.当时,为两圆公共弦所在的直线,方程为.
三、例题精讲
题型一直线方程、两直线的位置关系
例1已知两直线和.试确定、的值,使:
(1)与相交于点;
(2)∥;
(3)⊥,且在轴上的截距为-1.
【答案】(1),.
(2),时或,时,∥.
(3),
【解析】(1)由题意得,解得,.
(2)当时,显然不平行于;
当时,由,得 或.
即,时或,时,∥.
(3)当且仅当,即时,⊥.又,∴.
即,时,⊥,且在轴上的截距为-1.
【易错点】忽略对的情况的讨论
【思维点拨】遇到直线类题型,首先要注意特殊情况如斜率不存在时或时,并且对于直线平行和垂直时与和间的关系要熟练记忆。
例2如图,设一直线过点(-1,1),它被两平行直线l1:x+2y-1=0,l2:x+2y-3=0所截的线段的中点在直线l3:x-y-1=0上,求其方程.
【答案】.
【解析】与、平行且距离相等的直线方程为.
设所求直线方程为,即.又直线过,∴.解.∴所求直线方程为.
【易错点】求错与、平行且距离相等的直线方程
【思维点拨】本题的关键在于求到、平行且距离相等的直线方程,再利用这条直线求出和第三条支线的交点,从而求解本题.
题型二 圆的方程(对称问题、圆的几何性质运用)
例1已知实数、满足方程.
(1)求的最大值和最小值;
(2)求的最大值和最小值.
【答案】(1)的最大值为,最小值为.
(2)的最大值为,最小值为.
【解析】(1)原方程化为,表示以点为圆心,以为半径的圆.设,即,当直线与圆相切时,斜率取最大值和最小值,此时,解得.故的最大值为,最小值为.
(2)设,即,当与圆相切时,纵截距取得最大值和最小值,此时,即.故的最大值为,最小值为.
【易错点】理解错给定要求结果的含义
【思维点拨】正确理解给定结果的含义,在利用题中的条件解决问题。
例2已知点,为圆上一动点,当点在圆上运动时,的中点的轨迹方程是 .
【答案】.
【解析】设点为所求轨迹上任意一点,.
因为M为PQ的中点,所以即
又因为点在圆上,
所以,
故所求的轨迹方程为.
【易错点】中点的错误应用
【思维点拨】求出中点横纵坐标的方程及求出所求的直线
题型三 直线与圆、圆与圆的位置关系
例1在平面直角坐标系xOy中,已知圆C:x2+(y-3)2=2,点A是x轴上的一个动点,AP,AQ分别切圆C于P,Q两点,则线段PQ长的取值范围是 .
【答案】PQ∈.
【解析】设∠PCA=θ,所以PQ=2sin θ.
又cos θ=,AC∈[3,+∞),所以cos θ∈,
所以cos2θ∈,sin2θ=1-cos2θ∈,
所以sin θ∈,所以PQ∈.
【易错点】直接去求线段的长度
【思维点拨】转化思想,把要求的线段长度转化为角度的关系,从而解决问题.
例2已知圆
(1)若圆的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆外一点向该圆引一条切线,切点为为坐标原点,且有求使得取得最小值时点的坐标.
【答案】(1),或.
(2)
【解析】(1)将圆配方得.
当直线在两坐标轴上的截距为零时,设直线方程为 ,
由,解得,得.
当直线在两坐标轴上的截距不为零时,
设直线方程为,由,得,.
∴直线方程为,或.
(2)由,得,
即点在直线上.
当取最小值时,即取得最小值,直线,
∴直线的方程为.
得点的坐标为.
【易错点】没有分类讨论
【思维点拨】考查用点斜式、斜截式求直线的方法,利用分类讨论思想来解决问题
题型四 定点定值轨迹问题
例1已知t∈R,圆C:x2+y2-2tx-2t2y+4t-4=0.
(1)若圆C的圆心在直线x-y+2=0上,求圆C的方程.
(2)圆C是否过定点?如果过定点,求出定点的坐标;如果不过定点,请说明理由.
【答案】(1)圆C的方程为x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0.
(2)过定点,定点坐标为
【解析】(1)由原方程配方得(x-t)2+(y-t2)2=t4+t2-4t+4,其圆心为C(t,t2).
依题意知t-t2+2=0,所以t=-1或2.
即圆C的方程为x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0.
(2)整理圆C的方程为(x2+y2-4)+(-2x+4)t+(-2y)·t2=0,
令
所以圆C过定点(2,0).
【易错点】漏解
【思维点拨】判定圆是否过定点,或是求圆所过定点坐标的问题,可以在方程形式上转化为关于某个参量的方程,结合恒等式的关系,再构造关于x,y的方程组求该点的坐标.若方程组有解,则说明圆过定点,否则圆不过定点.
例2如图,已知圆C:x2+(y-3)2=4,一动直线l过点A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N.
(1)求证:当l与m垂直时,l必过圆心C.
(2)当PQ=2时,求直线l的方程.
(3)探索·是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
【答案】(1)见解析
(2)x=-1或4x-3y+4=0.
(3)·与直线l的倾斜角无关,且·=-5.
【解析】(1)因为l与m垂直,且km=-,所以kl=3.又kAC=3,所以当l与m垂直时,l的方程为y=3(x+1),l必过圆心C.
(2)①当直线l与x轴垂直时,易知x=-1,符合题意.
②当直线l与x轴不垂直时,
设直线l的方程为y=k(x+1),即kx-y+k=0.
因为PQ=2 ,所以CM==1,
则由CM==1,得k=,
所以直线l:4x-3y+4=0,
从而所求的直线l的方程为x=-1或4x-3y+4=0.
因为CM⊥MN,所以
·=(+)·=·+·=·.
①当l与x轴垂直时,易得N,
则=.又=(1,3),
所以·=·=-5;
②当l的斜率存在时,设直线l的方程为y=k(x+1),
则由得N,
则=,
所以·=·=+=-5.
综上,·与直线l的倾斜角无关,且·=-5.
【易错点】忽略对斜率不存在情况的讨论
【思维点拨】一般地,涉及到圆的切线或考虑其弦长问题时,若需要求直线的方程,则务必要全面考虑问题,即要考虑直线的斜率存在与不存在两种情况.
四、成果巩固
题型一直线方程、两直线的位置关系
1.已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
【答案】(1)当a=-1时,l1∥l2,否则l1与l2不平行
(2)a=
【解析】(1)由A1B2-A2B1=0,得a(a-1)-1×2=0,由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,
∴l1∥l2?,
故当a=-1时,l1∥l2,否则l1与l2不平行.
(2) 由A1A2+B1B2=0得a+2(a-1)=0?a=.
2.已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0,在坐标平面内求一点P,使PA=PB,且点P到直线l的距离为2.
【答案】P的坐标为或
【解析】设点P的坐标为(a,b),∵A(4,-3),B(2,-1),
∴线段AB的中点M的坐标为(3,-2),
∴线段AB的垂直平分线方程为y+2=x-3,即x-y-5=0.
∵点P(a,b)在上述直线上,∴a-b-5=0.①
又P(a,b)到直线l:4x+3y-2=0的距离为2,∴=2,即4a+3b-2=±10,②
联立①②可得或.∴所求点P的坐标为或.
3.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是________.
【答案】CD=2
【解析】由题意知点P关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),则光线所经过的路程PMN的长为CD=2.
题型二 圆的方程(对称问题、圆的几何性质运用)
1.根据下列条件,求圆的方程:
(1)经过P(-2,4)、Q(3,-1)两点,并且在x轴上截得的弦长等于6;
(2)圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2).
【答案】(1)x2+y2-2x-4y-8=0,或x2+y2-6x-8y=0
(2)(x-1)2+(y+4)2=8
【解析】(1)设圆的方程为x2+y2+Dx+Ey+F=0,
将P、Q点的坐标分别代入得
又令y=0,得x2+Dx+F=0.③
设x1,x2是方程③的两根,由|x1-x2|=6有D2-4F=36,④
由①、②、④解得D=-2,E=-4,F=-8,或D=-6,E=-8,F=0.
故所求圆的方程为x2+y2-2x-4y-8=0,或x2+y2-6x-8y=0.
(2) 如图,设圆心(x0,-4x0),依题意得=1,
∴x0=1,即圆心坐标为(1,-4),半径r=2,
故圆的方程为(x-1)2+(y+4)2=8.
2.在平面直角坐标系xOy中,二次函数f(x)=x2+2x+b(x∈R)与两坐标轴有三个交点.记过三个交点的圆为圆C.
(1)求圆C的方程;
(2)圆C是否经过定点(与b的取值无关)?证明你的结论.
【答案】(1)x2+y2+2x-(b+1)y+b=0.
(2)圆C必过定点(0,1),(-2,1)
【解析】(1)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,令y=0,得x2+Dx+F=0,这与x2+2x+b=0是同一个方程,故D=2,F=b;令x=0,得y2+Ey+b=0,此方程有一个根为b,代入得E=-b-1,所以圆C的方程为x2+y2+2x-(b+1)y+b=0.
(2)圆C必过定点(0,1),(-2,1).
证明如下:原方程转化为(x2+y2+2x-y)+b(1-y)=0,即解得或.
3.点P(4,-2)与圆x2+y2=4上任一点连线的中点轨迹方程是___________.
【答案】(x-2)2+(y+1)2=1
【解析】设圆上任一点坐标为(x0,y0),x+y=4,连线中点坐标为(x,y),
则?,代入x+y=4中得(x-2)2+(y+1)2=1.
题型三 直线与圆、圆与圆的位置关系
1.若过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤4}分为两部分,且使得这两部分的面积之差最大,则该直线的方程为 .
【答案】x+y-2=0
【解析】当圆心与点P的连线和过点P的直线垂直时,符合条件.圆心O与点P连线的斜率k=1,所以所求直线的斜率为-1,故所求直线方程为x+y-2=0.
2. 直线与圆相交于两点,若,则的取值范围是________.
【答案】
【解析】
设圆心为,弦的中点为,当时,
.∴当时,圆心到直线的距离.∴.∴,∴
3.若圆O:x2+y2=5与圆O1:(x-m)2+y2=20(m∈R)相交于A,B两点,且两圆在点A处的切线互相垂直,则线段AB的长是 .
【答案】
【解析】依题意得OO1==5,且△OO1A是直角三角形,=··OO1=·OA·AO1,因此AB===4.
题型四 定点定值轨迹问题
1. 如图,在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.设动圆C同时平分圆C1、圆C2的周长.
(1)求证:动圆圆心C在一条定直线上运动.
(2)动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
【答案】(1)动圆圆心C在定直线x+y-3=0上运动
(2)动圆C过定点,定点的坐标为和.
【解析】(1)设圆心C(x,y),由题意,得CC1=CC2,
即=,
化简得x+y-3=0,
即动圆圆心C在定直线x+y-3=0上运动.
(2)圆C过定点.
设C(m,3-m),则动圆C的半径为
=.
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理,得x2+y2-6y-2-2m(x-y+1)=0,
联立方程组
解得或
所以动圆C过定点,定点的坐标为和.
2. 已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1)若l1与圆相切,求直线l1的方程.
(2)若l1与圆相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM·AN是否为定值?若是,则求出定值;若不是,请说明理由.
【答案】(1)x=1或3x-4y-3=0.
(2)AM·AN是定值且为6.
【解析】(1)①若直线l1的斜率不存在,即直线为x=1,符合题意.
②若直线l1斜率存在,设直线l1的方程为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即=2,解得k=,
所以所求直线方程为x=1或3x-4y-3=0.
(2)方法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0.
由得N.
又因为直线CM与l1垂直,
由得M,
所以AM·AN=·
=·=6为定值.故AM·AN是定值且为6.
方法二:直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx-y-k=0.
由得N.
再由
得(1+k2)x2-(2k2+8k+6)x+k2+8k+21=0,
所以x1+x2=,得M.
以下同方法一.
方法三:(几何法)
(变式)
连接CA并延长交l2于点B,由题知kAC=2,=-,
所以CB⊥l2.
如图,△AMC∽△ABN,
所以=,
可得AM·AN=AC·AB=2·=6,是定值.
3. 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
【答案】(1)y=3或3x+4y-12=0.
(2)
【解析】(1)由得圆心C为(3,2),
因为圆C的半径为1,
所以圆C的方程为(x-3)2+(y-2)2=1.
由题知切线的斜率一定存在,
设所求圆C的切线方程为y=kx+3,即kx-y+3=0,
所以=1,所以|3k+1|=,
所以2k(4k+3)=0,所以k=0或k=-.
所以所求圆C的切线方程为y=3或y=-x+3,
即y=3或3x+4y-12=0.
(2)因为圆C的圆心在直线l:y=2x-4上,
所以设圆心C为(a,2a-4),
则圆C的方程为(x-a)2+[y-(2a-4)]2=1.
又因为MA=2MO,所以设点M(x,y),
则=2,整理得
x2+(y+1)2=4,设为圆D.
所以点M应该既在圆C上又在圆D上,即圆C和圆D有交点,所以|2-1|≤≤|2+1|,
由5a2-12a+8≥0得a∈R;
由5a2-12a≤0,得0≤a≤.
终上所述,实数a的取值范围为
五、课堂小结
1.有关直线的题目要注意对斜率存在与否进行讨论,直线的五种表达形式各有优缺点要随题意而定。
2.与圆有关的最值和范围的讨论常用以下方法:
(1)结合圆的方程的特点确定几何量之间的大小关系;
(2)函数值域求解法,即把所讨论的参数作为一个函数,一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的取值范围;
(3)利用不等式,若能将问题能转化为“和为定值”或“积为定值”,则可以用基本不等式求解.
3.定点问题的求解步骤:
(1)选参变量:需要证明过定点的动直线(曲线)往往随着某一个量的变化而变化,可以选择这个量为参变量(当涉及到的参变量较多时,也可以选择多个参变量);
(2)求动直线(曲线)方程:求出只含上述参变量的动直线(曲线)方程,并由其他条件减少参变量的个数,最终使方程中只含一个参变量;
(3)定点:求出定点坐标.不妨设方程中所含参变量为λ,把方程写为形如f(x,y)+λg(x,y)=0的形式,然后解关于x,y的方程组得到定点坐标.
2
1
同课章节目录
