【2019年高考理科数学三轮冲刺二项式定理教案
文档属性
| 名称 | 【2019年高考理科数学三轮冲刺二项式定理教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 00:00:00 | ||
图片预览



文档简介
2019年高考理科数学三论冲刺二项式定理
教材版本 全国通用 课时说明(建议) 120分钟
知识点 二项式定理的内容及相关概念、二项式的系数与项问题、二项式定理的应用
复习目标 熟练掌握二项式定理及其通项公式运用、二项式系数的性质,并能用它们计算和论证一些简单问题,培养学生的发散思维能力和逆向思维能力。
复习重点 二项式定理的展开公式
复习难点 二项式定理的应用
一、高考回顾
高考对二项式定理的考查.以二项式展开式及其通项公式内容为主.要有目标意识和构造意识.要注意展开式的通项公式正.反两方面的应用.此类题也可分两类.(1)直接运用通项公式求特定项的系数或与系数有关的问题.(2)需用转化思想化归为二项问题来处理的问题.?高考对本章的考查会保持相对稳定,即在题型、题量、难度、重点考查内容等方面不会有太大的变化。
二、知识清单
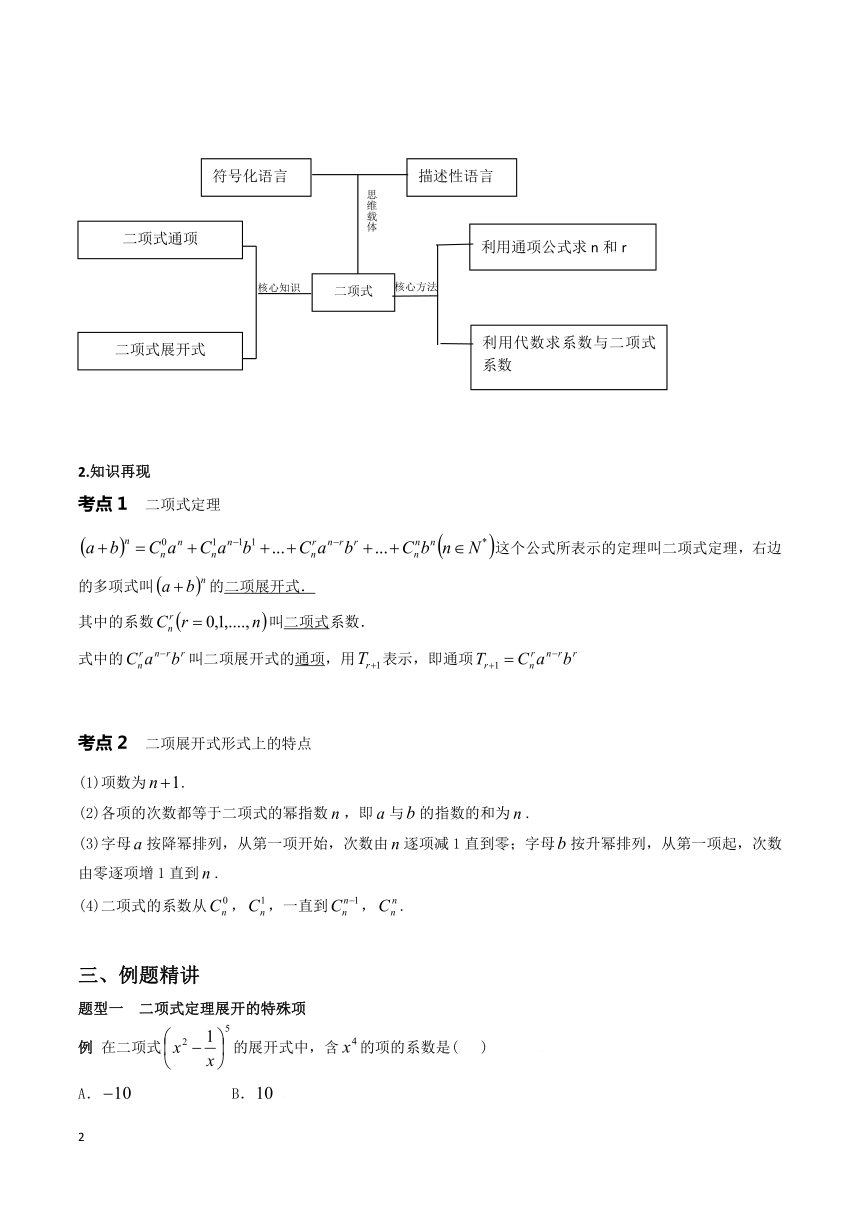
1.思维导图
2.知识再现
考点1 二项式定理
这个公式所表示的定理叫二项式定理,右边的多项式叫的二项展开式.
其中的系数叫二项式系数.
式中的叫二项展开式的通项,用表示,即通项
考点2 二项展开式形式上的特点
(1)项数为.
(2)各项的次数都等于二项式的幂指数,即与的指数的和为.
(3)字母按降幂排列,从第一项开始,次数由逐项减1直到零;字母按升幂排列,从第一项起,次数由零逐项增1直到.
(4)二项式的系数从,,一直到,.
三、例题精讲
题型一 二项式定理展开的特殊项
例 在二项式的展开式中,含的项的系数是( )
A. B.
C. D.5
【答案】B
【解析】对于,对于,则的项的系数是
【易错点】公式记错,计算错误。
【思维点拨】本题主要考查二项式定理的展开公式,知道什么是系数,会求每一项的系数.
题型二 求参数的值
例 若二项式的展开式中,第4项与第7项的二项式系数相等,则展开式的系数为________.(用数字作答)
【答案】9
【解析】根据已知条件可得: , 所以的展开式的通项为,令,所以所求系数为.
【易错点】分数指数幂的计算
【思维点拨】本题主要考查二项式定理的展开公式,并用其公式求参数的值.
题型三 展开项的系数和
例 已知,则等于( )
A. B. C. D.
【答案】B
【解析】由于,又的展开式的通项公式为:
,在展开式中是的系数,所以应取,
∴.
【易错点】对二项式的整体理解
【思维点拨】本题主要对二项式定理展开式的综合考查,学会构建模型
题型四 二项式定理中的赋值
二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和.
【答案】(1) (2)-1 (3)
【解析】设
(1)二项式系数之和为.
(2)各项系数之和为
(3)由(2)知,令,得,将两式相加,得,即为所有奇数项系数之和.
【思维点拨】本题主要学会赋值法求二项式系数和、系数和,难点在于赋值
四、成果巩固
题型一 二项式定理展开的特殊项
1.在 的展开式中,的系数为(?? )
A. B. C. D.
【答案】A
【解析】解:,的系数为
2.的展开式中 的系数是________
【答案】1120
【解析】解:,,解得,所以的系数为
3.在的展开式中,的系数是________ . (用数字作答)
【答案】
【解析】解:的展开式中,的系数是
题型二 求参数的值
1.(2017?山东)已知的展开式中含有的系数是54,则=________ .
【答案】4
【解析】解:的展开式中通项公式: ∵含有的系数是54,∴=2.
∴ ,可得 ,∴ ,解得.
2.在 的展开式中常数项的系数是60,则的值为________ .
【答案】2
【解析】解:,令,解得r=2.
∴ ,a>0,解得a=2.
3.【2015高考北京,理9】在的展开式中,的系数为 .(用数字作答)
【答案】40
【解析】利用通项公式,,令,得出的系数为
题型三 展开项的系数和
1.在 的展开式中,各项系数和与二项式系数和之比为64,则 的系数为(?? )
A.135 B.405 C.15 D.45
【答案】A
【解析】由题意可得,。,,,则的系数为
2.若二项式的展开式中各项的系数和为32,则该展开式中含的系数为(?? )
A.1 B.5 C.10 D.20
【答案】B
【解析】解:令,则, ∴
令 ,.∴该展开式中含x的系数为
3. 的二项展开式中第五项和第六项的二项式系数最大,则各项的系数和为________ .
【答案】-1
【解析】解:因为的展开式中第五项和第六项的二项式系数最大 所以=9
令
题型四 二项式定理中的赋值
1.已知,则实数的值为(?? )
A.15 B.20 C.40 D.60
【答案】D
【解析】解:其展开式的通项为 , 则x的系数为,解得, 则
2.若,且,则实数的值为 ( )
A.1或3 B.-3 C.1 D.1或-3
【答案】D
【解析】令=0,得,令=1,得,又,∴,∴=1或=-3.
3.【2015高考新课标2,理15】的展开式中x的奇数次幂项的系数之和为32,则__________.
【答案】3
【解析】由已知得,故的展开式中的奇数次冥项分别为,其系数之和为,解得=3
五、课堂小结
1、一个防范
运用二项式定理一定要牢记通项,注意与虽然相同,但具体到它们展开式的某一项时是不同的,一定要注意顺序问题,另外二项展开式的二项式系数与该项的(字母)系数是两个不同的概念,前者只指,而后者是字母外的部分.前者只与和有关,恒为正,后者还与,有关,可正可负.
2、一个定理
二项式定理可利用数学归纳法证明,也可根据次数,项数和系数利用排列组合的知识推导二项式定理.因此二项式定理是排列组合知识的发展和延续.
3、两种应用
(1)通项的应用:利用二项展开式的通项可求指定的项或指定项的系数等.
(2)展开式的应用:利用展开式①可证明与二项式系数有关的等式;②可证明不等式;③可证明整除问题;④可做近似计算等.
8
1
同课章节目录
