19.1.1 矩形的性质 试卷
图片预览


文档简介
19.1.1矩形的性质 同步练习
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
2.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.四边相等
3.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
A.12 B.14 C.16 D.18
4.如图,在矩形ABCD中,若∠1=40°,则两条对角线AC、BD所夹的锐角∠AOB的度数为( )
A.80° B.60° C.45° D.40°
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,若∠ACB=30°,AB=2,则BD的长为( )
A.4 B.3 C.2 D.1
6.如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是﹣1,则对角线AC、BD的交点表示的数是( )
A.5.5 B.5 C.6 D.6.5
二.填空题(每小题5分,共30分)
7.矩形具有而平行四边形不一定具有的性质是__________(填序号).
①对边平行且相等;②对角线互相平分;③对角相等;④对角线相等;⑤4个角都是90°.
8.如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是______.
9.如图,在矩形ABCD中,对角线AC与BD相交于O点,且AB=OA=2cm,则BD的长为_______cm.
10.如图,在矩形ABCD中,对角线AC和BD交于点O,若AC=4,则BD=________.
11. 矩形的一组邻边长分别为3cm、4cm,它的对角线长为_______,面积为_______.
12.已知矩形ABCD,过对角线BD的中点O作BD的垂直平分线EF,分别交AD,BC于点E,F,若△ABE的周长为7cm,则矩形ABCD的周长为_______ cm.
三、解答题(共40分)
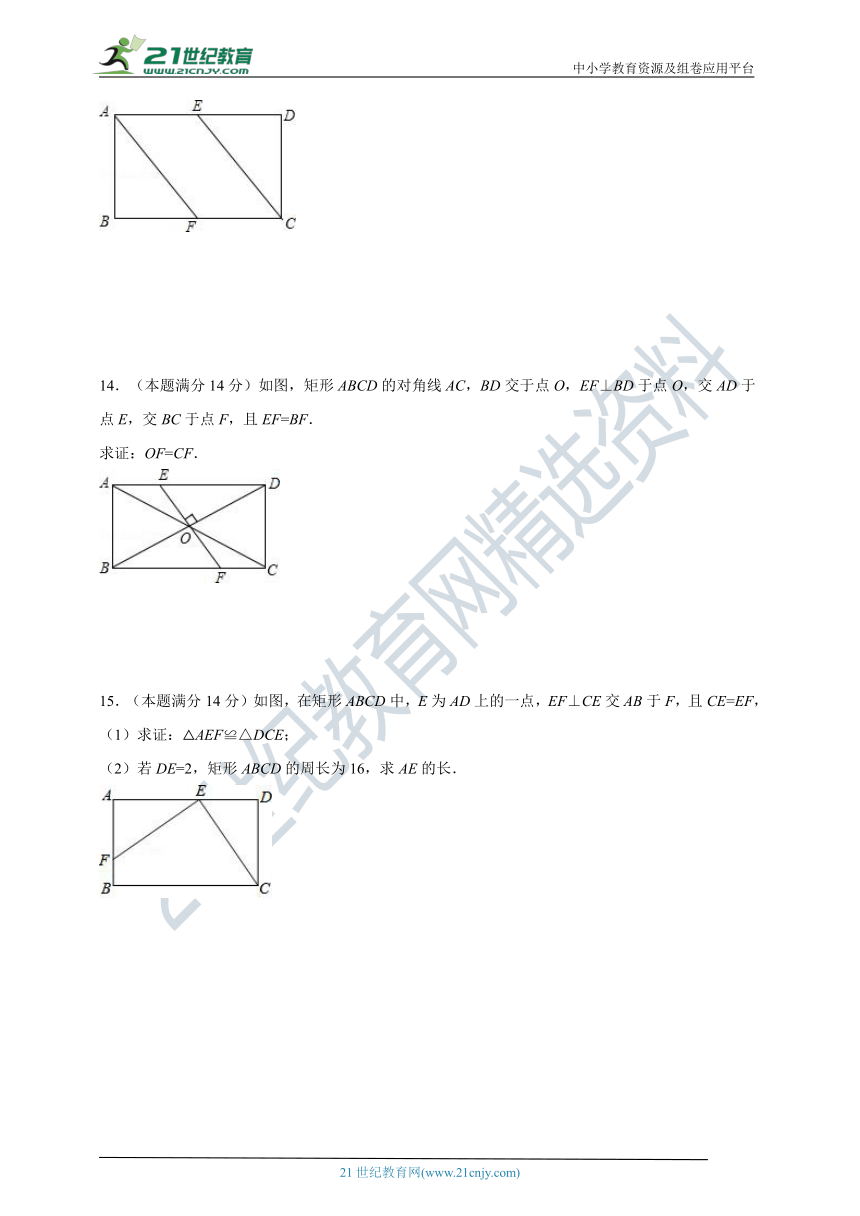
13.(本题满分12分)如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.
求证:△ABF≌△CDE.
14.(本题满分14分)如图,矩形ABCD的对角线AC,BD交于点O,EF⊥BD于点O,交AD于点E,交BC于点F,且EF=BF.
求证:OF=CF.
15.(本题满分14分)如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF,
(1)求证:△AEF≌△DCE;
(2)若DE=2,矩形ABCD的周长为16,求AE的长.
参考答案
一、选择题:
1.【答案】D.
【解析】∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误,故选D.
2.【答案】B.
【解析】∵矩形的对角线互相平分且相等,平行四边形的对角线互相平分;∴矩形具有而平行四边形不具有的性质是对角线相等;故选B.
3.【答案】A.
【解析】∵四边形ABCD是矩形,∴OA=AC=4,OB=BD,AC=BD,∴OA=OB,∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB=OA=OB=4,∴△ABO的周长=OA+OB+AB=12;故选A.
4.【答案】A.
【解析】∵矩形的性质对角线相等且互相平分,∴OB=OC,∴△BOC是等腰三角形,∴∠OBC=∠1,则∠AOB=2∠1=80°.故选A.
5.【答案】A.
【解析】在矩形ABCD中,∠ABC=90°,∵∠ACB=30°,AB=2,∴AC=2AB=2×2=4,∵四边形ABCD是矩形,∴BD=AC=4.故选A.
6.【答案】A.
【解析】连接BD交AC于E,如图所示:∵四边形ABCD是矩形,∴∠B=90°,AE=AC,∴AC===13,∴AE=6.5,∵点A表示的数是﹣1,∴OA=1,∴OE=AE﹣OA=5.5,∴点E表示的数是5.5,即对角线AC、BD的交点表示的数是5.5;故选A.
二、填空题:
7.【答案】④⑤.
【解析】矩形具有而平行四边形不一定具有的性质是:④对角线相等;⑤4个角都是90°.故答案为:④⑤.
8.【答案】4.
【解析】∵四边形ABCD是矩形,∴AC=2AO,BD=2BO,AC=BD,∴AO=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=2,即AC=2AO=4,故答案为:4.
9.【答案】4
【解析】∵矩形ABCD,∴OA=OC,OB=OD,AC=BD,∠ABC=90°,∴OA=OB,∵AB=OA=2,∴BD=AC=2OA=4.故答案为4.
10.【答案】4.
【解析】∵四边形ABCD是矩形,∴BD=AC,∵AC=4,∴BD=4.
11.【答案】5cm,12cm2.
【解析】∵四边形ABCD是矩形,∴∠ABC=90°,AC=BD,在Rt△ABC中,AB=3cm,BC=4cm,由勾股定理得:AC==5(cm),∴BD=AC=5cm,矩形ABCD的面积是AB×BC=3cm×4cm=12cm2.
12.【答案】14.
【解析】∵EF垂直平分BD,∴ED=EB,∵△ABE的周长为7cm,∴AB+AE+BE=AB+AE+DE=AB+AD=7cm,∴矩形ABCD的周长为14cm.
三、解答题:
13.【答案】见解析.
【解析】证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,∵点E是AD的中点,点F是BC的中点,∴DE=AD BF=BC,∴BF=DE,在△ABF和△CDE中,∵,∴△ABF≌△CDE(SAS).
14.【答案】见解析.
【解析】证明:在矩形ABCD中,OA=OC,AD∥BC,∴∠OAE=∠OCF,在△AOE和△COF中,∵,∴△AOE≌△COF(ASA),∴OE=OF,∵EF=BF,∴BF=2OF,∵EF⊥BD,∴在Rt△BOF中,∠OBC=30°,∠BFO=90°﹣30°=60°,又∵矩形ABCD中,OB=OC,∴∠OCB=30°,∴∠COF=∠BFO﹣∠OCB=60°﹣30°=30°,∴∠OCB=∠COF,∴OF=CF.
15.【答案】(1)见解析;(2)3.
【解析】证明:(1)∵四边形ABCD是矩形,∴∠A=∠D=90°,∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,又∵∠AEF+∠AFE=90°,∴∠AFE=∠DEC,在△AEF和△DCE中,,∴△AEF≌△DCE(AAS);
(2)∵△AEF≌△DCE,∴AE=CD,∵2(AD+CD)=16,DE=2,∴2(AE+2+AE)=16,∴AE=3.
时间:30分钟,总分:100分 班级:_____________ 姓名:_____________
一、选择题(每小题5分,共30分)
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
2.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分 B.对角线相等 C.对角线互相垂直 D.四边相等
3.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
A.12 B.14 C.16 D.18
4.如图,在矩形ABCD中,若∠1=40°,则两条对角线AC、BD所夹的锐角∠AOB的度数为( )
A.80° B.60° C.45° D.40°
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,若∠ACB=30°,AB=2,则BD的长为( )
A.4 B.3 C.2 D.1
6.如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是﹣1,则对角线AC、BD的交点表示的数是( )
A.5.5 B.5 C.6 D.6.5
二.填空题(每小题5分,共30分)
7.矩形具有而平行四边形不一定具有的性质是__________(填序号).
①对边平行且相等;②对角线互相平分;③对角相等;④对角线相等;⑤4个角都是90°.
8.如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是______.
9.如图,在矩形ABCD中,对角线AC与BD相交于O点,且AB=OA=2cm,则BD的长为_______cm.
10.如图,在矩形ABCD中,对角线AC和BD交于点O,若AC=4,则BD=________.
11. 矩形的一组邻边长分别为3cm、4cm,它的对角线长为_______,面积为_______.
12.已知矩形ABCD,过对角线BD的中点O作BD的垂直平分线EF,分别交AD,BC于点E,F,若△ABE的周长为7cm,则矩形ABCD的周长为_______ cm.
三、解答题(共40分)
13.(本题满分12分)如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.
求证:△ABF≌△CDE.
14.(本题满分14分)如图,矩形ABCD的对角线AC,BD交于点O,EF⊥BD于点O,交AD于点E,交BC于点F,且EF=BF.
求证:OF=CF.
15.(本题满分14分)如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF,
(1)求证:△AEF≌△DCE;
(2)若DE=2,矩形ABCD的周长为16,求AE的长.
参考答案
一、选择题:
1.【答案】D.
【解析】∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误,故选D.
2.【答案】B.
【解析】∵矩形的对角线互相平分且相等,平行四边形的对角线互相平分;∴矩形具有而平行四边形不具有的性质是对角线相等;故选B.
3.【答案】A.
【解析】∵四边形ABCD是矩形,∴OA=AC=4,OB=BD,AC=BD,∴OA=OB,∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB=OA=OB=4,∴△ABO的周长=OA+OB+AB=12;故选A.
4.【答案】A.
【解析】∵矩形的性质对角线相等且互相平分,∴OB=OC,∴△BOC是等腰三角形,∴∠OBC=∠1,则∠AOB=2∠1=80°.故选A.
5.【答案】A.
【解析】在矩形ABCD中,∠ABC=90°,∵∠ACB=30°,AB=2,∴AC=2AB=2×2=4,∵四边形ABCD是矩形,∴BD=AC=4.故选A.
6.【答案】A.
【解析】连接BD交AC于E,如图所示:∵四边形ABCD是矩形,∴∠B=90°,AE=AC,∴AC===13,∴AE=6.5,∵点A表示的数是﹣1,∴OA=1,∴OE=AE﹣OA=5.5,∴点E表示的数是5.5,即对角线AC、BD的交点表示的数是5.5;故选A.
二、填空题:
7.【答案】④⑤.
【解析】矩形具有而平行四边形不一定具有的性质是:④对角线相等;⑤4个角都是90°.故答案为:④⑤.
8.【答案】4.
【解析】∵四边形ABCD是矩形,∴AC=2AO,BD=2BO,AC=BD,∴AO=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=2,即AC=2AO=4,故答案为:4.
9.【答案】4
【解析】∵矩形ABCD,∴OA=OC,OB=OD,AC=BD,∠ABC=90°,∴OA=OB,∵AB=OA=2,∴BD=AC=2OA=4.故答案为4.
10.【答案】4.
【解析】∵四边形ABCD是矩形,∴BD=AC,∵AC=4,∴BD=4.
11.【答案】5cm,12cm2.
【解析】∵四边形ABCD是矩形,∴∠ABC=90°,AC=BD,在Rt△ABC中,AB=3cm,BC=4cm,由勾股定理得:AC==5(cm),∴BD=AC=5cm,矩形ABCD的面积是AB×BC=3cm×4cm=12cm2.
12.【答案】14.
【解析】∵EF垂直平分BD,∴ED=EB,∵△ABE的周长为7cm,∴AB+AE+BE=AB+AE+DE=AB+AD=7cm,∴矩形ABCD的周长为14cm.
三、解答题:
13.【答案】见解析.
【解析】证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,∵点E是AD的中点,点F是BC的中点,∴DE=AD BF=BC,∴BF=DE,在△ABF和△CDE中,∵,∴△ABF≌△CDE(SAS).
14.【答案】见解析.
【解析】证明:在矩形ABCD中,OA=OC,AD∥BC,∴∠OAE=∠OCF,在△AOE和△COF中,∵,∴△AOE≌△COF(ASA),∴OE=OF,∵EF=BF,∴BF=2OF,∵EF⊥BD,∴在Rt△BOF中,∠OBC=30°,∠BFO=90°﹣30°=60°,又∵矩形ABCD中,OB=OC,∴∠OCB=30°,∴∠COF=∠BFO﹣∠OCB=60°﹣30°=30°,∴∠OCB=∠COF,∴OF=CF.
15.【答案】(1)见解析;(2)3.
【解析】证明:(1)∵四边形ABCD是矩形,∴∠A=∠D=90°,∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,又∵∠AEF+∠AFE=90°,∴∠AFE=∠DEC,在△AEF和△DCE中,,∴△AEF≌△DCE(AAS);
(2)∵△AEF≌△DCE,∴AE=CD,∵2(AD+CD)=16,DE=2,∴2(AE+2+AE)=16,∴AE=3.
