鲁教版数学七下10.4线段的垂直平分线课件(21张ppt)
文档属性
| 名称 | 鲁教版数学七下10.4线段的垂直平分线课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1008.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 10:40:06 | ||
图片预览








文档简介
为了方便广饶居民的生活,计划在乐安大街公路旁修建一个购物中心,使它到A、B两个小区的距离相等,请问购物中心应建于何处?
A
B
生活中的数学
1.理解并掌握线段垂直平分线的性质定理及逆定理,
并能用它们进行相关的计算及证明
2.掌握线段垂直平分线的尺规作图及作法的证明.
学习目标:
探究活动一
1.思考?
怎样用折纸的方法画出线段AB的垂直平分线MN?
2.在MN上任取一点P,连结PA、PB;度量一下PA、PB的长度,你有什么发现?
3.PA=PB
猜想:
线段垂直平分线上的点,和这条线段两个端点的距离相等
猜想验证
几何画板验证
命题:
线段垂直平分线上的点,和这条线段两个端点的距离相等
命题证明
P
已知:如图直线MN⊥AB,垂足为C,且AC=CB.点P在直线MN上
求证:PA=PB
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
已知:如图直线MN⊥AB,垂足为C,且AC=CB.点P在直线MN上
求证:PA=PB
命题证明
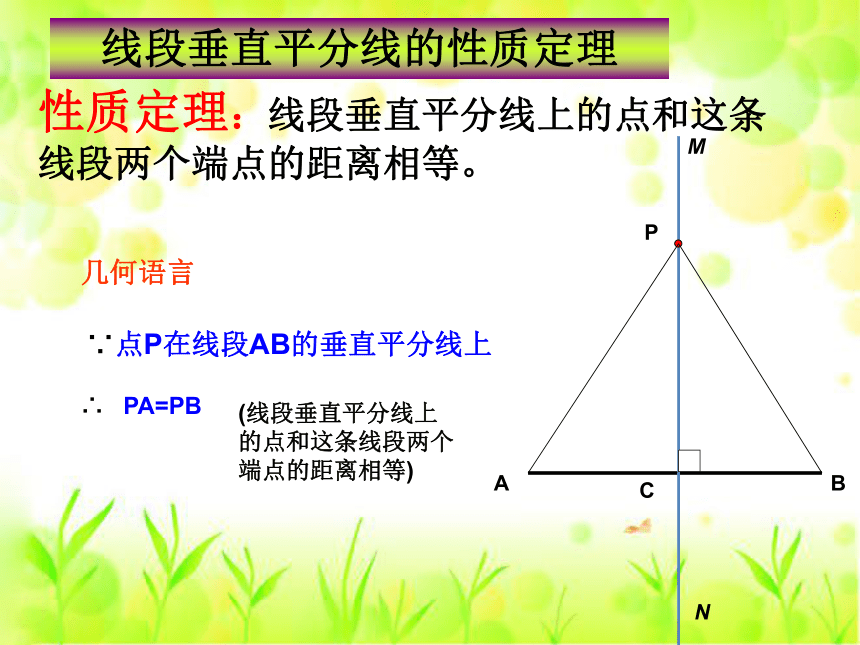
性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。
C
几何语言
∴
∵点P在线段AB的垂直平分线上
PA=PB
(线段垂直平分线上的点和这条线段两个端点的距离相等)
线段垂直平分线的性质定理
1、如图,线段MN被直线AB垂直平分,图中有哪些相等的线段?
基础练习:
EM=EN
FM=FN
BM=BN
OM=ON
2.如图P是AB垂直平分线MN上一点,连结PA、PB,则∠A与∠B( )
A.∠A﹥∠B B. ∠A﹤∠B
C. ∠A=∠B
M
N
P
A
B
C
基础练习:
C
反过来,如果PA=PB,
那么点P是否在线段AB的垂
直平分线上呢?
探究活动二
猜想验证
猜想:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
C
已知:PA =PB,
求证:点P 在线段AB 的垂直平分线上.
证明:过点P 作PC⊥AB ,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
到线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言:
∵ PA =PB
∴ 点P在线段AB垂直平分线上
线段垂直平分线的判定定理
线段的垂直平分线的尺规作图.
复习回顾
提示:用今天我们学习的垂直平分线的判定定理
探究活动三
怎样证明我们的作法是正确的?
M
N
已知:
线段AB,AC=AD=BC=BD
求证:
线段CD是AB的垂直平分线
证明:
作法证明
为了方便广饶居民的生活,计划在乐安大街公路旁修建一个购物中心,使它到A、B、两个小区的距离相等,请问购物中心应建于何处?
A
B
回顾实际问题
问题解决
已知:如图,在 △ABC 中,AB = AC, O 是 △ABC 内一点,且 OB = OC.
求证:直线 AO 垂直平分线段BC.
典例剖析
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段的垂直平分线
C
谈收获
布 置 作 业
必做题:课本121页第3题 .
选做题:配套练习册第108页 第7题.
A
B
生活中的数学
1.理解并掌握线段垂直平分线的性质定理及逆定理,
并能用它们进行相关的计算及证明
2.掌握线段垂直平分线的尺规作图及作法的证明.
学习目标:
探究活动一
1.思考?
怎样用折纸的方法画出线段AB的垂直平分线MN?
2.在MN上任取一点P,连结PA、PB;度量一下PA、PB的长度,你有什么发现?
3.PA=PB
猜想:
线段垂直平分线上的点,和这条线段两个端点的距离相等
猜想验证
几何画板验证
命题:
线段垂直平分线上的点,和这条线段两个端点的距离相等
命题证明
P
已知:如图直线MN⊥AB,垂足为C,且AC=CB.点P在直线MN上
求证:PA=PB
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
已知:如图直线MN⊥AB,垂足为C,且AC=CB.点P在直线MN上
求证:PA=PB
命题证明
性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。
C
几何语言
∴
∵点P在线段AB的垂直平分线上
PA=PB
(线段垂直平分线上的点和这条线段两个端点的距离相等)
线段垂直平分线的性质定理
1、如图,线段MN被直线AB垂直平分,图中有哪些相等的线段?
基础练习:
EM=EN
FM=FN
BM=BN
OM=ON
2.如图P是AB垂直平分线MN上一点,连结PA、PB,则∠A与∠B( )
A.∠A﹥∠B B. ∠A﹤∠B
C. ∠A=∠B
M
N
P
A
B
C
基础练习:
C
反过来,如果PA=PB,
那么点P是否在线段AB的垂
直平分线上呢?
探究活动二
猜想验证
猜想:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
C
已知:PA =PB,
求证:点P 在线段AB 的垂直平分线上.
证明:过点P 作PC⊥AB ,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
到线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言:
∵ PA =PB
∴ 点P在线段AB垂直平分线上
线段垂直平分线的判定定理
线段的垂直平分线的尺规作图.
复习回顾
提示:用今天我们学习的垂直平分线的判定定理
探究活动三
怎样证明我们的作法是正确的?
M
N
已知:
线段AB,AC=AD=BC=BD
求证:
线段CD是AB的垂直平分线
证明:
作法证明
为了方便广饶居民的生活,计划在乐安大街公路旁修建一个购物中心,使它到A、B、两个小区的距离相等,请问购物中心应建于何处?
A
B
回顾实际问题
问题解决
已知:如图,在 △ABC 中,AB = AC, O 是 △ABC 内一点,且 OB = OC.
求证:直线 AO 垂直平分线段BC.
典例剖析
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段的垂直平分线
C
谈收获
布 置 作 业
必做题:课本121页第3题 .
选做题:配套练习册第108页 第7题.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
