人教版小学数学五年级下册《图形与几何1》课件(19张PPT幻灯片)
文档属性
| 名称 | 人教版小学数学五年级下册《图形与几何1》课件(19张PPT幻灯片) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 13:28:34 | ||
图片预览






文档简介
图形与几何(1)
人教版小学数学五年级下册
一、复习导入
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
思考
第一单元学习了观察物体。
第三单元学习了长方体和正方体。
第五单元学习了图形的运动。
你学到了什么,说说你的收获吧!
我认识了长方体和正方体。
我会画旋转后的图形样子。
我探究出了体积公式的计算方法……
大家说得不够完善,今天我们就来系统地复习一下。
二、知识梳理
问题
观察物体要注意什么?有什么规律?
根据从一个方向看到的平面图形摆出的立体图形不一定相同。
1.
2.
根据从三个方向看到的平面图形确定的立体图形的形状一定相同。
你是这样想的吗?
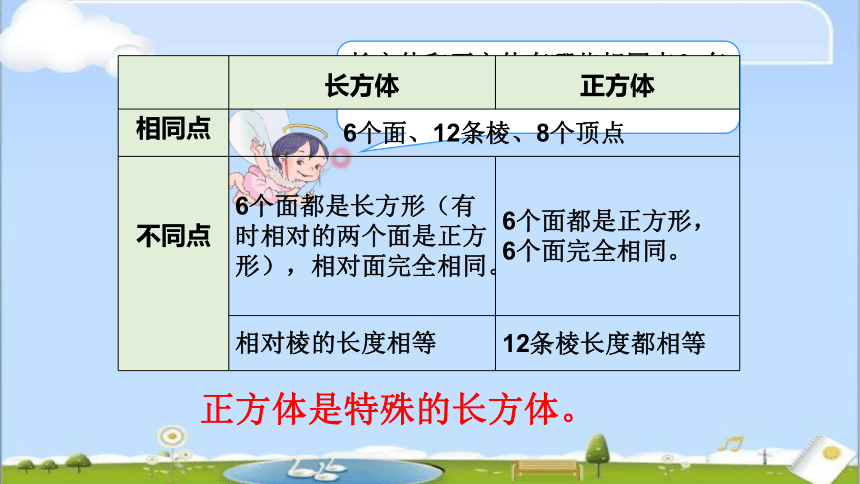
长方体和正方体有哪些相同点?有哪些不同点?
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
问
正方体和长方体的表面积的计算公式是什么?
正方体的表面积=边长×边长×6,用字母表示是S=6a2;长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示是S=(ab+ah+bh)×2。
问
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高,用字母表示是V=abh;正方体的体积=棱长×棱长×棱长,用字母表示是V=a3。
什么运动是旋转?旋转有什么特点?
思考
图形的旋转是图形上的每一点在平面上绕某个旋转中心旋转一定角度的位置移动。
你能举例说明吗?
旋转前后图形的大小和形状没有改变;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点。
下面3个图形都是由棱长1cm的小正方体摆成的。
连一连。
下面3个图形都是由棱长1cm的小正方体摆成的。
①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
问题
你是怎么想的?
数出小正方体的个数就可以了。
棱长为1 cm的小正方体的体积是1 cm3。
6 cm3
10 cm3
11 cm3
①的体积是③的体积的 。
如果要把①、②、③分别继续补搭成一个大正方体,每个图形至少还需要多少个小正方体?
怎样做比较简便?
要补成大正方体,则图形的正面、侧面和上面的都是正方形,且小正方体个数都得一样多。
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
左图怎样变换可以得到右图呢?
左边图形以O点为旋转中心,分别顺时针旋转90°,180°,270°,就可得到右边的图形。
O
图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?
问题
绿色部分所占方格数:
红色部分所占方格数:
4×2=8
绿色部分占整个图案:
红色部分占整个图案:
三、巩固深化
1.观察右边的图形,填一填。
(1) 图形①绕O点 方向旋转
90°到图形 所在的位置;
(2) 图形②绕O点 方向旋转
90°到图形 所在的位置;
(3)图形③绕O点 方向旋转90°到图形 所
在的位置。
顺时针
②
顺时针
③
顺时针
④
2.填空题。
(1)一个棱长是2m的正方体,它的表面积是( )m2,体积是( )m3。
(2)1.36L= ( )cm3 3.25小时= ( )分钟
(3)一个正方体纸盒的棱长总和是36cm,它的表面积是( )cm2,体积是( )cm3。
(4)一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的( )倍。
24
8
1360
195
54
27
27
3.一个装满沙子的长方体沙坑长7米、宽3米、深0.8米,每立方米沙子重1400千克,这个沙坑里共装沙子多少吨?
解答:
7×3×0.8×1400÷1000
=23.52(吨)
答:这个沙坑里共装沙子23.52吨。
谈收获!
五、课后作业
1.课本P119,第11题;
2.完成练习册本课时的习题。
谢谢!
人教版小学数学五年级下册
一、复习导入
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
思考
第一单元学习了观察物体。
第三单元学习了长方体和正方体。
第五单元学习了图形的运动。
你学到了什么,说说你的收获吧!
我认识了长方体和正方体。
我会画旋转后的图形样子。
我探究出了体积公式的计算方法……
大家说得不够完善,今天我们就来系统地复习一下。
二、知识梳理
问题
观察物体要注意什么?有什么规律?
根据从一个方向看到的平面图形摆出的立体图形不一定相同。
1.
2.
根据从三个方向看到的平面图形确定的立体图形的形状一定相同。
你是这样想的吗?
长方体和正方体有哪些相同点?有哪些不同点?
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
问
正方体和长方体的表面积的计算公式是什么?
正方体的表面积=边长×边长×6,用字母表示是S=6a2;长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示是S=(ab+ah+bh)×2。
问
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高,用字母表示是V=abh;正方体的体积=棱长×棱长×棱长,用字母表示是V=a3。
什么运动是旋转?旋转有什么特点?
思考
图形的旋转是图形上的每一点在平面上绕某个旋转中心旋转一定角度的位置移动。
你能举例说明吗?
旋转前后图形的大小和形状没有改变;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点。
下面3个图形都是由棱长1cm的小正方体摆成的。
连一连。
下面3个图形都是由棱长1cm的小正方体摆成的。
①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
问题
你是怎么想的?
数出小正方体的个数就可以了。
棱长为1 cm的小正方体的体积是1 cm3。
6 cm3
10 cm3
11 cm3
①的体积是③的体积的 。
如果要把①、②、③分别继续补搭成一个大正方体,每个图形至少还需要多少个小正方体?
怎样做比较简便?
要补成大正方体,则图形的正面、侧面和上面的都是正方形,且小正方体个数都得一样多。
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
左图怎样变换可以得到右图呢?
左边图形以O点为旋转中心,分别顺时针旋转90°,180°,270°,就可得到右边的图形。
O
图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?
问题
绿色部分所占方格数:
红色部分所占方格数:
4×2=8
绿色部分占整个图案:
红色部分占整个图案:
三、巩固深化
1.观察右边的图形,填一填。
(1) 图形①绕O点 方向旋转
90°到图形 所在的位置;
(2) 图形②绕O点 方向旋转
90°到图形 所在的位置;
(3)图形③绕O点 方向旋转90°到图形 所
在的位置。
顺时针
②
顺时针
③
顺时针
④
2.填空题。
(1)一个棱长是2m的正方体,它的表面积是( )m2,体积是( )m3。
(2)1.36L= ( )cm3 3.25小时= ( )分钟
(3)一个正方体纸盒的棱长总和是36cm,它的表面积是( )cm2,体积是( )cm3。
(4)一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的( )倍。
24
8
1360
195
54
27
27
3.一个装满沙子的长方体沙坑长7米、宽3米、深0.8米,每立方米沙子重1400千克,这个沙坑里共装沙子多少吨?
解答:
7×3×0.8×1400÷1000
=23.52(吨)
答:这个沙坑里共装沙子23.52吨。
谈收获!
五、课后作业
1.课本P119,第11题;
2.完成练习册本课时的习题。
谢谢!
