北师大版八年级数学下册第二章一元一次不等式和一元一次不等式组复习课件(87张)
文档属性
| 名称 | 北师大版八年级数学下册第二章一元一次不等式和一元一次不等式组复习课件(87张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 00:00:00 | ||
图片预览











文档简介
课件87张PPT。第二章 一元一次不等式与一元一次不等式组
专题一 本章知识梳理
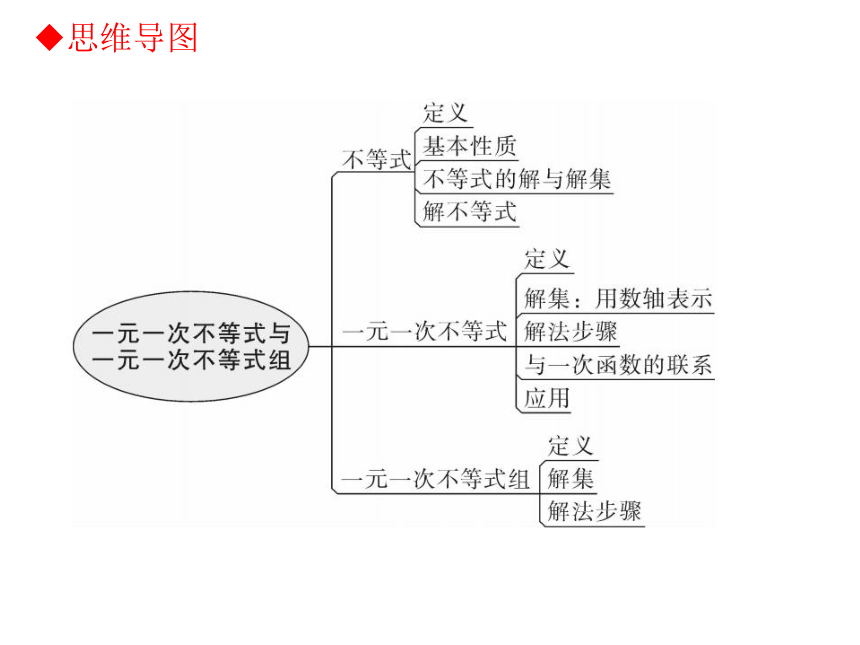
?思维导图?考纲要求1. 结合具体问题,了解不等式的意义,探索不等式的基本性质.
2. 会解数字系数的一元一次不等式,并能在数轴上表示出解集;会用数轴确定由两个一元一次不等式组成的不等式组的解集.
3. 能够根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题. ?知识梳理1. 不等式
(1)定义:一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做________.
(2)基本性质:①如果a>b,那么____________________; ②如果a>b,且c>0,那
么______________; ③如果a>b,且c<0,那么
________________. 不等式a+c>b+c,a-c>b-cac>bc或ac①若a>b,则b___a;②若a>b,且b>c,则a___c;③若a-b>0,则a___b,若a-b<0,则a___b,反之,亦成立;④若ab>0,则a,b___号,若ab<0,则a,b___号,反之,亦成立;⑤若a≥b,且b≤a,则a___b;⑥若a2≤0,则a___0.
(4)不等式的解:能使不等式成立的__________,叫做不等式的解. <>><同异==未知数的值?知识梳理(5)不等式的解集:一个含有未知数的不等式的________,组成这个不等式的解集.
(6)解不等式:求不等式______的过程叫做解不等式.
(7)不等式解集的表示方法
①用不等式表示. 一般地,一个含未知数的不等式有无数个解,其解集是某个范围,这个范围可用一个最简单的不等式表示出来,例如x+3<6的解集是x<3.所有解解集?知识梳理②用数轴表示. 在数轴上某点处画空心圆圈表示________这一点(“>”或“<”),画实心圆点表示_______这一点(“≥”或“≤”),大于向_______画,小于向_______画.
2. 一元一次不等式
(1)定义:不等式的左右两边都是________,只含有________未知数,并且未知数的最高次数是_______,像这样的不等式,叫做一元一次不等式. 不包括包括右左整式一个1?知识梳理(2)解法步骤:①去分母;②去括号;③移项;④合并同类项;⑤未知数的系数化为1.
3. 一元一次不等式与一次函数
(1)用一次函数的图象确定一元一次不等式ax+b>0(或ax+b<0)的解集
要确定ax+b>0(或ax+b<0)的解集,可以利用一次函数y=ax+b在直角坐标系中的图象. 根据x轴上方图象上的点的纵坐标_______0,x轴下方图象上的点的纵坐标_______0,大于小于?知识梳理可以确定一次函数y=ax+b的图象在x轴_______的部分所对应的自变量x的取值范围是不等式ax+b>0的解集;一次函数y=ax+b的图象在x轴________的部分所对应的自变量x的取值范围是不等式ax+b<0的解集.
上方下方?知识梳理(2)用一次函数的图象确定一元一次不等式ax+b>cx+d(或ax+b对于ax+b>cx+d(或ax+by2(或y1一次函数与一元一次不等式常用来解决实际问题中的方案决策型问题,即通过对两种不同方案的分析比较,选出更为合算的方案,如购物优惠方案、最大利润方案、最小支出方案等.
解此类问题的一般步骤是:①根据已知条件,列出两种方案相关的一次函数表达式;②再根据两个一次函数的大小关系(分大于、等于、小于三种)分别求得相应的x值;③最后比较所得结果,根据题目要求作出决策即可.?知识梳理4. 一元一次不等式组
(1)定义:一般地,关于________未知数的几个_____________合在一起,就组成一个一元一次不等式组.
(2)解集
①一元一次不等式组中各个不等式的解集的__________,叫做这个一元一次不等式组的解集. 如果不等式的解集无公共部分,就说这个不等式组________.
同一个一元一次不等式公共部分无解?知识梳理②一元一次不等式组的解集的确定方法有两种:①利用数轴,②利用规律口诀,如下表所示:?知识梳理(3)解法步骤:①利用解一元一次不等式的方法分别求出不等式组中各个不等式的解集;
②利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集. 专题二 本章易错点归总?易错点易错点 1误用不等式的性质3而致错
不等式的基本性质3是“不等式两边乘(或除以)同一个负数,不等号的方向改变”,而在实际解题中,学生往往忽略这一点,忘记改变不等号的方向.
【例1】解不等式
易错提示:当做到-5x>-1这一步时,虽然学生平时背诵了不等式的基本性质3,但容易粗心或片面追求解题速度而忘记改变不等号的方向,导致出现错误x> .
?易错点?学以致用1. 解不等式: ,并把它的解集在如图Z2-1所示的数轴上表示出来. ?易错点易错点2 去分母时,忽视分数线的括号作用而致错
解不等式,要注意分子的整体性,不可忽视分数线的括号作用,特别是去分母时,若分子是多项式,则必须先添括号,再进行计算.
【例2】解不等式 ,并把解集在数轴上表示出来. ?易错点?学以致用2. 解不等式 解:去分母,得10-2(2-3x)<5(1+x).
去括号,得10-4+6x<5+5x.
移项,得6x-5x<5-10+4.
合并同类项,得x<-1. ?易错点易错点 3解不等式(组)的应用题时,忽略问题的实际意义,未正确选取特殊值而致错
解不等式(组)的应用题,兼顾到实际意义,往往有一些隐含条件,需要根据题目的数量只能取某几个正整数,因此,在解完不等式(组)后,要检验一下不等式的解集,既要满足不等式,又要符合实际意义. ?易错点【例3】某公司为了扩大生产,决定购进6台机器,但所用资金不能超过68万元,现有甲、乙两种机器供选择,其中甲种机器每台14万元,乙种机器每台10万元,现按该公司要求有哪几种购买方案,并说明理由.
易错提示:本题设未知数列不等式可解得x≤2,但之后可能只取x=1或2的情况,漏掉了x=0,导致答案不完整. ?易错点正解:设购买甲型号的机器为x台,则乙种型号的机器为(6-x)台, 依题意,得14x+10(6-x)≤68.解得x≤2.∵x≥0,且x为整数,∴x=0,x=1或x=2.
∴该公司共有三种购买方案如下.
方案一甲种机器0台,则购买乙种机器6台;
方案二甲种机器1台,则购买乙种机器5台;
方案三甲种机器2台,则购买乙种机器4台. ?学以致用3. 学校将若干间宿舍分配给七年级一班的女生住宿,已知该班女生少于35人,若每个房间住5人,则剩下5人没处住,若每个房间住8人,则空一间房,并且还有一间房也不满. 最多有多少间宿舍,多少名女生?专题三 本章重要考点专练——解一元一次不等式一、选择题 1. 不等式x+1≥2的解集在数轴上表示正确的是( )A2. 不等式 的解集是( ) A. x≤4 B. x≥4 C. x≤-1 D. x≥-1 3. 不等式6-4x≥3x-8的非负整数解为( ) A. 2个 B. 3个 C. 4个 D. 5个
AB4. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A. -3<b<-2 B. -3<b≤-2
C. -3≤b≤-2 D. -3≤b<-2
二、填空题
5. 不等式 的解集是________. Dx>-36. 不等式5x-3<3x+5的最大整数解是_____.
7. 不等式 的解集为x>1,则m的值为_____.
8. 已知实数x,y满足2x-3y=4,并且x≥-1,y<2,现有k=x-y,则k的取值范围是__________. 31≤k<34三、解答题
9. 解下列不等式:
(1)4x+5≤2(x+1); (2) ;
(3) ; (4) ≥3(x-1)-4.
解:(1)去括号,得4x+5≤2x+2.
移项、合并同类项,得2x≤-3.
系数化为1,得x≤- .
(4)去分母,得x+1≥6(x-1)-8.
去括号,得x+1≥6x-6-8.
移项,得x-6x≥-6-8-1.
合并同类项,得-5x≥-15.
系数化为1,得x≤3. (2)去分母,得2x>6-3(x-2).
去括号,得2x>6-3x+6.
移项、合并同类项,得5x>12.
系数化为1,得x> .
(3)去分母,得3(x-2)≤2(7-x).
去括号,得3x-6≤14-2x.
移项、合并同类项,得5x≤20.
系数化为1,得x≤4.
10. 解不等式 ,并把解集在如图Z2-3所示的数轴上表示出来.
解:不等式两边同时乘6,得3x-6≤14-2x.
移项、合并同类项,得5x≤20.
系数化为1,得x≤4.
将其在数轴上表示出来如答图Z2-2所示.
11. 解不等式 ,并将解集在如图Z2-4所示的数轴上表示出来.
解:去分母,得1+x<3x-3.
移项,得x-3x<-3-1.
合并同类项,得-2x<-4.
系数化为1,得x>2.
将解集表示在数轴上如答图Z2-3. 12. 已知不等式5-3x≤1的最小整数解是关于x的方程(a+9)x=4(x+1)的解,求a的值.
解:解不等式5-3x≤1,得x≥ .
所以不等式的最小整数解是2.
把x=2代入方程(a+9)x=4(x+1),得
(a+9)×2=4×(2+1).
解得a=-3.
专题四 本章重要考点专练——一元一次不等式与一次函数一、选择题
1. 一次函数y=ax+b的图象如图Z2-5所示,则不等式ax+b≥0的解集是( )
A. x≥2
B. x≤2
C. x≥4
D. x≤4B2. 如图Z2-6,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )A3. 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A. x≤3 B. x≥3 C. x≥-3 D. x≤0
4. 如图Z2-7,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
AC二、填空题
5. 如图Z2-8,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是________. x>16. 如图Z2-9,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b≤-2x的解集为__________. -2≤x≤-17. 如图Z2-10,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解是______. -38. 已知直线y1=x,y2= x+1,y3= x+5的图象如图Z2-11所示,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为_________. 三、解答题
9. 如图Z2-12,直线y1=-2x+1与直线y2=x-5交于点A.
(1)求点A的坐标;
(2)请直接写出当y1<y2,y1=y2,y1>y2时,对应的x的取值范围. 10. 如图Z2-13,已知直线y1=
x+1与x轴交于点A,与直线y2= x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围. 11. 如图Z2-14,在平面直角坐标系xOy中,直线l1:y=k1x+b过点A(0,-3),B(5,2),直线l2:y=k2x+2.
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值. 12. 如图Z2-15,直线y=kx+b分别与x轴、y轴交于点A(-2,0),B(0,3);直线y=1-mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1-mx的解集是x> .
(1)分别求出k,b,m的值;
(2)求S△ACD. 专题五 本章重要考点专练——一元一次不等式的应用一、选择题
1. 三个连续正整数的和小于39,这样的正整数中,最大一组的和是( )
A. 39 B. 36
C. 35 D. 34
B2. 为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品. 已知乒乓球的单价为1.5元,乒乓球拍的单价为25元,如果购买总金额不超过200元,且尽可能多的购买乒乓球拍,则小张同学最多可购买乒乓球拍( )
A. 5副 B. 6副
C. 7副 D. 8副B3. 现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( )
A. 4辆 B. 5辆
C. 6辆 D. 7辆C二、填空题
4. 某苗圃计划培育甲,乙两种树苗共2 000棵,据统计这两种树苗的成活率分别为94%和99%,要使这批树苗的成活率不低于96%,求培育甲种树苗至多多少棵?设培育甲种树苗x棵,根据题意列出的不等式是__________________________________. 94%x+99%(2 000-x)≥96%×2 0005. 某种商品的进价为每件100元,商场按进价提高50%后标价,为增加销量,准备打折销售,但要保证利润率不低于20%,则至多可以打_______折.
6. 某种商品的进价为15元,出售时标价是22.5元. 由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价________元出售该商品.86 7. 2016年在东安县举办了永州市首届中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分,负一场积0分. 某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是__________. 8三、解答题
8. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物. 我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一. 2016年全国谷子种植面积为2 000万亩,年总产量为150万吨,我省谷子平均亩产量为160 kg,国内其他地区谷子的平均亩产量为60 kg,请解答下列问题:
(1)求我省2016年谷子的种植面积是多少万亩;
(2)2017年,若我省谷子的平均亩产量仍保持160 kg不变,要使我省谷子的年总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子?
9. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满. 已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完,求租用小客车数量的最大值. 10. 在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
11. 某校“棋乐无穷”社团前两次购买的两种材质的象棋采购如下表(近期两种材质象棋的售价一直不变):(1)若该社团计划再采购这两种材质的象棋各5盒,则需要多少元?
(2)若该社团准备购买这两种材质的象棋共50盒,且要求塑料象棋的数量不多于玻璃象棋数量的3倍,请设计出最省钱的购买方案,并说明理由. 12. 甲乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过200元后,超过200元的部分按85%收费,在乙商场累计超过100元后,超出部分按照90%收费.
(1)若小王要购置累计500元的商品,他去哪个商场花费少?
(2)若一顾客累计购物花费x(x>200)元,当x在什么范围内,到乙商场购物花费比较少?解:(1)甲商场购置累计500元的商品花费为200+300×85%=455(元),
乙商场购置累计500元的商品花费为100+400×90%=460(元),
∵455<460,
∴他去甲商场花费少.
(2)若到乙商场购物花费较少,则
200+(x-200)×85%>100+(x-100)×90%.
解得x<400.
∴当200<x<400时,到乙商场购物花费较少.
专题六 本章重要考点专练——解一元一次不等式组一、选择题
1. 不等式组 的解集表示在数轴上正确的是( )C2. 不等式组 的解集为( )
A. x<3 B. x≥2
C. 2≤x<3 D. 2<x<3C3. 在关于x,y的方程组
中,未知数满足x≥0,y>0,那么m的取值范围在数轴上应表示为( )C4. 关于x的不等式组
的解集为x<3,那么m的取值范围为( )
A. m=3 B. m>3
C. m<3 D. m≥3D二、填空题
5. 不等式组
的解集为__________.
6. 不等式组
的解集是x>-1,则a的取值范围是_________. 1<x≤47. 若关于x的一元一次不等式组 无解,则a的取值范围是_________.
8. 已知不等式组
在同一条数轴上表示不等式①②的解集如图Z2-16所示,则b-a的值为_______. a≧1三、解答题
9. 解下列不等式组:10. 解不等式组
并把它的解集在如图Z2-17所示的数轴上表示出来. 解:解不等式2x≥-9-x,得x≥-3.
解不等式5x-1>3(x+1),得x>2.
则不等式组的解集为x>2.
将解集表示在数轴上如答图Z2-4所示. 11. 求不等式(2x-1)(x+3)>0的解集.
专题一 本章知识梳理
?思维导图?考纲要求1. 结合具体问题,了解不等式的意义,探索不等式的基本性质.
2. 会解数字系数的一元一次不等式,并能在数轴上表示出解集;会用数轴确定由两个一元一次不等式组成的不等式组的解集.
3. 能够根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题. ?知识梳理1. 不等式
(1)定义:一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做________.
(2)基本性质:①如果a>b,那么____________________; ②如果a>b,且c>0,那
么______________; ③如果a>b,且c<0,那么
________________. 不等式a+c>b+c,a-c>b-cac>bc或ac
(4)不等式的解:能使不等式成立的__________,叫做不等式的解. <>><同异==未知数的值?知识梳理(5)不等式的解集:一个含有未知数的不等式的________,组成这个不等式的解集.
(6)解不等式:求不等式______的过程叫做解不等式.
(7)不等式解集的表示方法
①用不等式表示. 一般地,一个含未知数的不等式有无数个解,其解集是某个范围,这个范围可用一个最简单的不等式表示出来,例如x+3<6的解集是x<3.所有解解集?知识梳理②用数轴表示. 在数轴上某点处画空心圆圈表示________这一点(“>”或“<”),画实心圆点表示_______这一点(“≥”或“≤”),大于向_______画,小于向_______画.
2. 一元一次不等式
(1)定义:不等式的左右两边都是________,只含有________未知数,并且未知数的最高次数是_______,像这样的不等式,叫做一元一次不等式. 不包括包括右左整式一个1?知识梳理(2)解法步骤:①去分母;②去括号;③移项;④合并同类项;⑤未知数的系数化为1.
3. 一元一次不等式与一次函数
(1)用一次函数的图象确定一元一次不等式ax+b>0(或ax+b<0)的解集
要确定ax+b>0(或ax+b<0)的解集,可以利用一次函数y=ax+b在直角坐标系中的图象. 根据x轴上方图象上的点的纵坐标_______0,x轴下方图象上的点的纵坐标_______0,大于小于?知识梳理可以确定一次函数y=ax+b的图象在x轴_______的部分所对应的自变量x的取值范围是不等式ax+b>0的解集;一次函数y=ax+b的图象在x轴________的部分所对应的自变量x的取值范围是不等式ax+b<0的解集.
上方下方?知识梳理(2)用一次函数的图象确定一元一次不等式ax+b>cx+d(或ax+b
解此类问题的一般步骤是:①根据已知条件,列出两种方案相关的一次函数表达式;②再根据两个一次函数的大小关系(分大于、等于、小于三种)分别求得相应的x值;③最后比较所得结果,根据题目要求作出决策即可.?知识梳理4. 一元一次不等式组
(1)定义:一般地,关于________未知数的几个_____________合在一起,就组成一个一元一次不等式组.
(2)解集
①一元一次不等式组中各个不等式的解集的__________,叫做这个一元一次不等式组的解集. 如果不等式的解集无公共部分,就说这个不等式组________.
同一个一元一次不等式公共部分无解?知识梳理②一元一次不等式组的解集的确定方法有两种:①利用数轴,②利用规律口诀,如下表所示:?知识梳理(3)解法步骤:①利用解一元一次不等式的方法分别求出不等式组中各个不等式的解集;
②利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集. 专题二 本章易错点归总?易错点易错点 1误用不等式的性质3而致错
不等式的基本性质3是“不等式两边乘(或除以)同一个负数,不等号的方向改变”,而在实际解题中,学生往往忽略这一点,忘记改变不等号的方向.
【例1】解不等式
易错提示:当做到-5x>-1这一步时,虽然学生平时背诵了不等式的基本性质3,但容易粗心或片面追求解题速度而忘记改变不等号的方向,导致出现错误x> .
?易错点?学以致用1. 解不等式: ,并把它的解集在如图Z2-1所示的数轴上表示出来. ?易错点易错点2 去分母时,忽视分数线的括号作用而致错
解不等式,要注意分子的整体性,不可忽视分数线的括号作用,特别是去分母时,若分子是多项式,则必须先添括号,再进行计算.
【例2】解不等式 ,并把解集在数轴上表示出来. ?易错点?学以致用2. 解不等式 解:去分母,得10-2(2-3x)<5(1+x).
去括号,得10-4+6x<5+5x.
移项,得6x-5x<5-10+4.
合并同类项,得x<-1. ?易错点易错点 3解不等式(组)的应用题时,忽略问题的实际意义,未正确选取特殊值而致错
解不等式(组)的应用题,兼顾到实际意义,往往有一些隐含条件,需要根据题目的数量只能取某几个正整数,因此,在解完不等式(组)后,要检验一下不等式的解集,既要满足不等式,又要符合实际意义. ?易错点【例3】某公司为了扩大生产,决定购进6台机器,但所用资金不能超过68万元,现有甲、乙两种机器供选择,其中甲种机器每台14万元,乙种机器每台10万元,现按该公司要求有哪几种购买方案,并说明理由.
易错提示:本题设未知数列不等式可解得x≤2,但之后可能只取x=1或2的情况,漏掉了x=0,导致答案不完整. ?易错点正解:设购买甲型号的机器为x台,则乙种型号的机器为(6-x)台, 依题意,得14x+10(6-x)≤68.解得x≤2.∵x≥0,且x为整数,∴x=0,x=1或x=2.
∴该公司共有三种购买方案如下.
方案一甲种机器0台,则购买乙种机器6台;
方案二甲种机器1台,则购买乙种机器5台;
方案三甲种机器2台,则购买乙种机器4台. ?学以致用3. 学校将若干间宿舍分配给七年级一班的女生住宿,已知该班女生少于35人,若每个房间住5人,则剩下5人没处住,若每个房间住8人,则空一间房,并且还有一间房也不满. 最多有多少间宿舍,多少名女生?专题三 本章重要考点专练——解一元一次不等式一、选择题 1. 不等式x+1≥2的解集在数轴上表示正确的是( )A2. 不等式 的解集是( ) A. x≤4 B. x≥4 C. x≤-1 D. x≥-1 3. 不等式6-4x≥3x-8的非负整数解为( ) A. 2个 B. 3个 C. 4个 D. 5个
AB4. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A. -3<b<-2 B. -3<b≤-2
C. -3≤b≤-2 D. -3≤b<-2
二、填空题
5. 不等式 的解集是________. Dx>-36. 不等式5x-3<3x+5的最大整数解是_____.
7. 不等式 的解集为x>1,则m的值为_____.
8. 已知实数x,y满足2x-3y=4,并且x≥-1,y<2,现有k=x-y,则k的取值范围是__________. 31≤k<34三、解答题
9. 解下列不等式:
(1)4x+5≤2(x+1); (2) ;
(3) ; (4) ≥3(x-1)-4.
解:(1)去括号,得4x+5≤2x+2.
移项、合并同类项,得2x≤-3.
系数化为1,得x≤- .
(4)去分母,得x+1≥6(x-1)-8.
去括号,得x+1≥6x-6-8.
移项,得x-6x≥-6-8-1.
合并同类项,得-5x≥-15.
系数化为1,得x≤3. (2)去分母,得2x>6-3(x-2).
去括号,得2x>6-3x+6.
移项、合并同类项,得5x>12.
系数化为1,得x> .
(3)去分母,得3(x-2)≤2(7-x).
去括号,得3x-6≤14-2x.
移项、合并同类项,得5x≤20.
系数化为1,得x≤4.
10. 解不等式 ,并把解集在如图Z2-3所示的数轴上表示出来.
解:不等式两边同时乘6,得3x-6≤14-2x.
移项、合并同类项,得5x≤20.
系数化为1,得x≤4.
将其在数轴上表示出来如答图Z2-2所示.
11. 解不等式 ,并将解集在如图Z2-4所示的数轴上表示出来.
解:去分母,得1+x<3x-3.
移项,得x-3x<-3-1.
合并同类项,得-2x<-4.
系数化为1,得x>2.
将解集表示在数轴上如答图Z2-3. 12. 已知不等式5-3x≤1的最小整数解是关于x的方程(a+9)x=4(x+1)的解,求a的值.
解:解不等式5-3x≤1,得x≥ .
所以不等式的最小整数解是2.
把x=2代入方程(a+9)x=4(x+1),得
(a+9)×2=4×(2+1).
解得a=-3.
专题四 本章重要考点专练——一元一次不等式与一次函数一、选择题
1. 一次函数y=ax+b的图象如图Z2-5所示,则不等式ax+b≥0的解集是( )
A. x≥2
B. x≤2
C. x≥4
D. x≤4B2. 如图Z2-6,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )A3. 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A. x≤3 B. x≥3 C. x≥-3 D. x≤0
4. 如图Z2-7,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
AC二、填空题
5. 如图Z2-8,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是________. x>16. 如图Z2-9,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b≤-2x的解集为__________. -2≤x≤-17. 如图Z2-10,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解是______. -38. 已知直线y1=x,y2= x+1,y3= x+5的图象如图Z2-11所示,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为_________. 三、解答题
9. 如图Z2-12,直线y1=-2x+1与直线y2=x-5交于点A.
(1)求点A的坐标;
(2)请直接写出当y1<y2,y1=y2,y1>y2时,对应的x的取值范围. 10. 如图Z2-13,已知直线y1=
x+1与x轴交于点A,与直线y2= x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围. 11. 如图Z2-14,在平面直角坐标系xOy中,直线l1:y=k1x+b过点A(0,-3),B(5,2),直线l2:y=k2x+2.
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值. 12. 如图Z2-15,直线y=kx+b分别与x轴、y轴交于点A(-2,0),B(0,3);直线y=1-mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1-mx的解集是x> .
(1)分别求出k,b,m的值;
(2)求S△ACD. 专题五 本章重要考点专练——一元一次不等式的应用一、选择题
1. 三个连续正整数的和小于39,这样的正整数中,最大一组的和是( )
A. 39 B. 36
C. 35 D. 34
B2. 为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品. 已知乒乓球的单价为1.5元,乒乓球拍的单价为25元,如果购买总金额不超过200元,且尽可能多的购买乒乓球拍,则小张同学最多可购买乒乓球拍( )
A. 5副 B. 6副
C. 7副 D. 8副B3. 现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( )
A. 4辆 B. 5辆
C. 6辆 D. 7辆C二、填空题
4. 某苗圃计划培育甲,乙两种树苗共2 000棵,据统计这两种树苗的成活率分别为94%和99%,要使这批树苗的成活率不低于96%,求培育甲种树苗至多多少棵?设培育甲种树苗x棵,根据题意列出的不等式是__________________________________. 94%x+99%(2 000-x)≥96%×2 0005. 某种商品的进价为每件100元,商场按进价提高50%后标价,为增加销量,准备打折销售,但要保证利润率不低于20%,则至多可以打_______折.
6. 某种商品的进价为15元,出售时标价是22.5元. 由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价________元出售该商品.86 7. 2016年在东安县举办了永州市首届中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分,负一场积0分. 某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是__________. 8三、解答题
8. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物. 我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一. 2016年全国谷子种植面积为2 000万亩,年总产量为150万吨,我省谷子平均亩产量为160 kg,国内其他地区谷子的平均亩产量为60 kg,请解答下列问题:
(1)求我省2016年谷子的种植面积是多少万亩;
(2)2017年,若我省谷子的平均亩产量仍保持160 kg不变,要使我省谷子的年总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子?
9. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满. 已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完,求租用小客车数量的最大值. 10. 在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
11. 某校“棋乐无穷”社团前两次购买的两种材质的象棋采购如下表(近期两种材质象棋的售价一直不变):(1)若该社团计划再采购这两种材质的象棋各5盒,则需要多少元?
(2)若该社团准备购买这两种材质的象棋共50盒,且要求塑料象棋的数量不多于玻璃象棋数量的3倍,请设计出最省钱的购买方案,并说明理由. 12. 甲乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过200元后,超过200元的部分按85%收费,在乙商场累计超过100元后,超出部分按照90%收费.
(1)若小王要购置累计500元的商品,他去哪个商场花费少?
(2)若一顾客累计购物花费x(x>200)元,当x在什么范围内,到乙商场购物花费比较少?解:(1)甲商场购置累计500元的商品花费为200+300×85%=455(元),
乙商场购置累计500元的商品花费为100+400×90%=460(元),
∵455<460,
∴他去甲商场花费少.
(2)若到乙商场购物花费较少,则
200+(x-200)×85%>100+(x-100)×90%.
解得x<400.
∴当200<x<400时,到乙商场购物花费较少.
专题六 本章重要考点专练——解一元一次不等式组一、选择题
1. 不等式组 的解集表示在数轴上正确的是( )C2. 不等式组 的解集为( )
A. x<3 B. x≥2
C. 2≤x<3 D. 2<x<3C3. 在关于x,y的方程组
中,未知数满足x≥0,y>0,那么m的取值范围在数轴上应表示为( )C4. 关于x的不等式组
的解集为x<3,那么m的取值范围为( )
A. m=3 B. m>3
C. m<3 D. m≥3D二、填空题
5. 不等式组
的解集为__________.
6. 不等式组
的解集是x>-1,则a的取值范围是_________. 1<x≤47. 若关于x的一元一次不等式组 无解,则a的取值范围是_________.
8. 已知不等式组
在同一条数轴上表示不等式①②的解集如图Z2-16所示,则b-a的值为_______. a≧1三、解答题
9. 解下列不等式组:10. 解不等式组
并把它的解集在如图Z2-17所示的数轴上表示出来. 解:解不等式2x≥-9-x,得x≥-3.
解不等式5x-1>3(x+1),得x>2.
则不等式组的解集为x>2.
将解集表示在数轴上如答图Z2-4所示. 11. 求不等式(2x-1)(x+3)>0的解集.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
