北师大版八年级数学下册章节冲刺训练课件:第六章平行四边形(66张PPT)
文档属性
| 名称 | 北师大版八年级数学下册章节冲刺训练课件:第六章平行四边形(66张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-09 20:43:03 | ||
图片预览









文档简介
课件66张PPT。
第六章 平行四边形
专题一 本章知识梳理
?思维导图?考纲要求1. 理解平行四边形的概念.
2. 探索并证明平行四边形的有关性质定理:平行四边形的对边相等、对角相等、对角线互相平分;探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
3. 探索并证明三角形中位线定理.
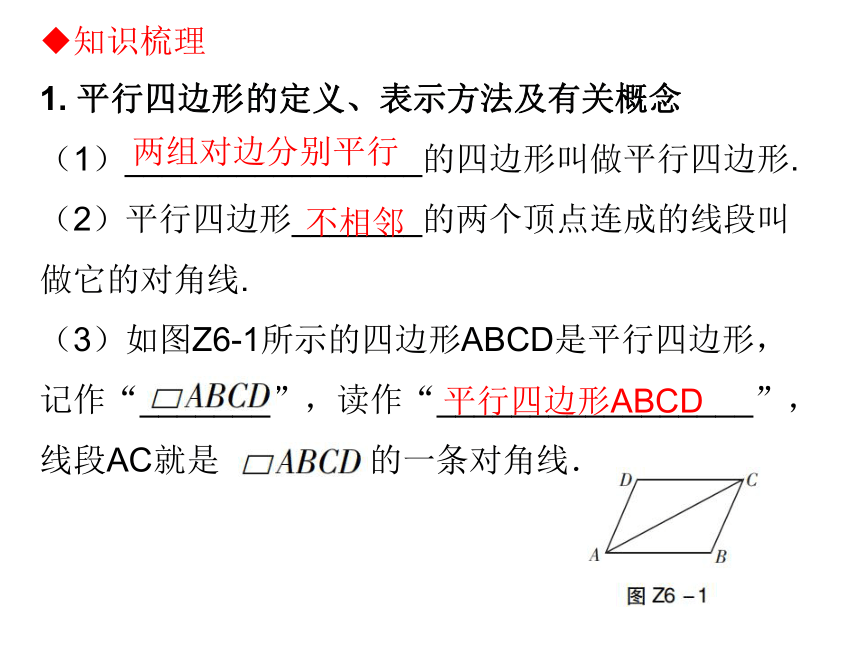
4. 探索并掌握多边形内角和与外角和公式.?知识梳理1. 平行四边形的定义、表示方法及有关概念
(1)________________的四边形叫做平行四边形.
(2)平行四边形_______的两个顶点连成的线段叫做它的对角线.
(3)如图Z6-1所示的四边形ABCD是平行四边形,记作“_______”,读作“_________________”,线段AC就是 的一条对角线.两组对边分别平行不相邻平行四边形ABCD?知识梳理2. 平行四边形的对称性
平行四边形是______对称图形,_________________是它的对称中心.
3. 多边形的内角和定理
(1)四边形可以被从同一个顶点出发的对角线分成_____个三角形,五边形可以被从同一个顶点出发的对角线分成_____个三角形……n边形可以被从同一个顶点出发的对角线分成________个三角形.
中心两条对角线的交点23(n-2)?知识梳理(2)多边形的内角和定理:n边形的内角和等于__________(n是大于或等于3的自然数).
4. 多边形的外角及外角和定理
(1)多边形内角的一边与另一边的__________所组成的角叫做这个多边形的外角.
(2)在多边形的每一个顶点处取这个多边形的一个________,它们的和叫做这个多边形的外角和.
(3)多边形的外角和定理:多边形的外角和都等于________. (n-2)·180°反向延长线外角360°专题二 本章易错点归总易错点1 不能正确选用平行四边形的判定方法而致错
在解题过程中,有时误用条件而导致判断出错,凭主观想象就判断一个四边形是平行四边形.
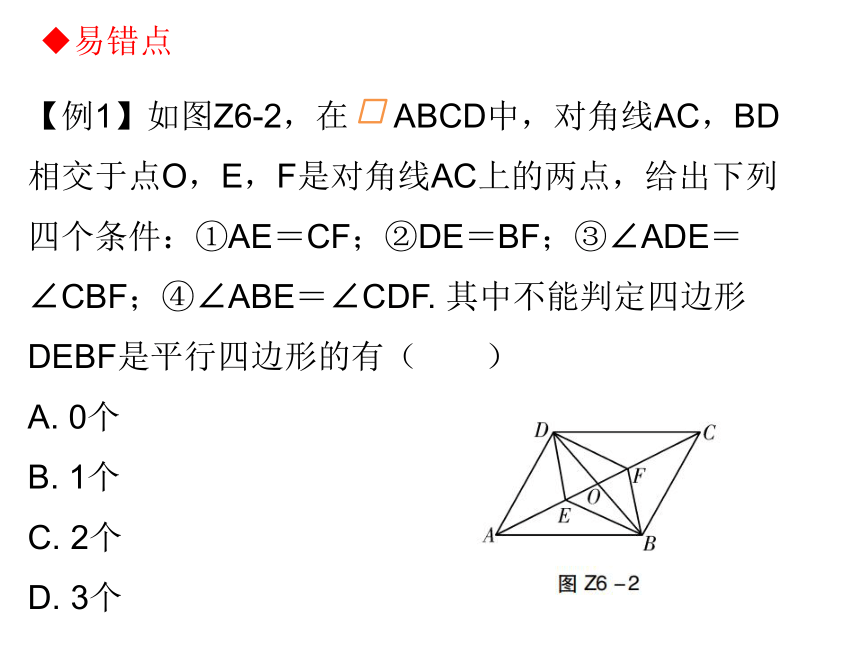
?易错点【例1】如图Z6-2,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF. 其中不能判定四边形DEBF是平行四边形的有( )
A. 0个
B. 1个
C. 2个
D. 3个 ?易错点易错提示:易出现对判定定理理解不透,想当然没有深入证明而出错.
?易错点正解:根据平行四边形的定义或判定定理逐一判断即可.
答案:B1. 能判定四边形ABCD为平行四边形的题设是( )
A. AB=AD,CB=CD
B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D
D. AB∥CD,AD=BC?学以致用B易错点2 考虑不周,导致错解或漏解
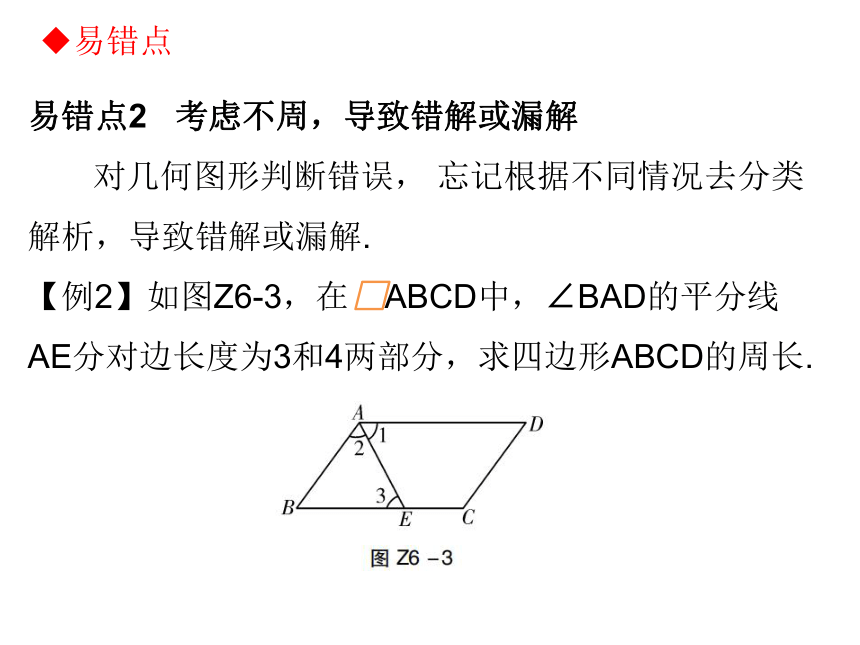
对几何图形判断错误, 忘记根据不同情况去分类解析,导致错解或漏解.
【例2】如图Z6-3,在 ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长. ?易错点易错提示:在 ABCD中,易得BC=AD=7,△ABE是等腰三角形,然后分别从BE=3或4去求解即可求得答案. 易出现考虑不全而造成漏解.
?易错点正解:∵在 ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,∴BC=AD=3+4=7,AD∥BC,AB=CD,∠1=∠2. ∴∠1=∠3. ∴∠2=∠3,∴AB=BE. 然后分别从BE=3或4去分析求解以免考虑不全而造成漏解. ①若BE=3,则AB=CD=3,此时四边形ABCD的周长为2×(3+7)=20;②若BE=4,则AB=CD=4,此时四边形ABCD的周长为2×(4+7)=22. ∴四边形ABCD的周长为20或22. ?易错点 2. 已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是_______________.?学以致用75°或15°专题三 本章重要考点专练——平行四边形的性质与判定一、选择题
1. 如图Z6-4,在 ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
A. 6
B. 12
C. 18
D. 24B2. 如图Z6-5,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A.
B. 2
C.
D. 4C3. 如图Z6-6,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
A. 1个
B. 2个
C. 3个
D. 4个D4. 如图Z6-7,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A. 2
B. 1
C.
D. B二、填空题
5. 已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=__________. 4或-26. 如图Z6-8,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F. 若∠EAF=56°,则∠B=______°. 567. 如图Z6-9,将 ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是__________. (7,4)三、解答题
8. 如图Z6-10,E是 ABCD的边AD的中点,连接CE并延长交BA的延长线于点F,若CD=6,求BF的长. 9. 如图Z6-11,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形. 10. 如图Z6-12,在 ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
求证:BC=BF. 11. 如图Z6-13,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF,BD,求证:四边形ABDF是平行四边形. 12. 如图Z6-14,在 ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°. 求∠B的度数. 专题四 本章重要考点专练——三角形的中位线一、选择题
1. 如图Z6-15,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为点D,OD=50 cm,当它的一端B着地时,另一端A离地面的高度AC为
( )
A. 25 cm
B. 50 cm
C. 75 cm
D. 100 cmD2. 如图Z6-16,点D,E,F分别为△ABC各边的中点,下列说法正确的是( )
A. DE=DF
B. EF= AB
C. S△ABD=S△ACD
D. AD平分∠BACC3. 如图Z6-17,在△ABC中,∠ABC=90°,AB=8,BC=6. 若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为
( )
A. 7
B. 8
C. 9
D. 10B4. 如图Z6-18,在△ABC中,AB=AC,点E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是
( )
A. ∠ECD=112.5°
B. DE平分∠FDC
C. ∠DEC=30°
D. AB= CDC二、填空题
5. 如图Z6-19,A,B两点被池塘隔开,不能直接测量其距离. 于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200 m,则A,B间的距离为__________m. 1006. 如图Z6-20,在Rt△ABC中,∠C=90°,BC=6,AC=8,点D,E分别为AC,AB的中点,连接DE,则△ADE的面积是_________. 67. 如图Z6-21,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=5,AC=3,则DF的长为________. 18. 如图Z6-22,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,…,如此操作下去,则第n个小三角形的
面积为__________. 三、解答题
9. 如图Z6-23,在△ABC中,CD是高,CE是中线,CE=CB,点A,D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE. 若AC=18,BC=12,求△CEG的周长. 10. 如图Z6-24,等边△ABC的边长是2,点D,E分别为AB,AC的中点,延长BC至点F,使CF= BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长. 11.如图Z6-25,四边形ABCD为平行四边形,点E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点. 判断CH与DG的位置关系,并说明理由. 12. 如图Z6-26,点M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长. 专题五 本章重要考点专练——多边形的内角和与外角和一、选择题
1. 若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A. 3 B. 4 C. 5 D. 6
2. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70AC3. 如图Z6-27,将图Z6-27①中五边形纸片ABCDE的A点以BE为折线往下折,A点恰好落在CD上,如图Z6-27②所示,再分别以图中的AB,AE为折线,将C,D两点往上折,使得A,B,C,D,E五点均在同一平面上,如图Z6-27③所示,若图Z6-27①中∠A=124°,则图Z6-27③中∠CAD的度数为何( )
A. 56°
B. 60°
C. 62°
D. 68°D二、填空题
4. 正八边形的每个外角的度数为__________.
5. 若多边形的每一个内角均为135°,则这个多边形的边数为__________. 45°86.如图Z6-28所示的正六边形ABCDEF,连接FD,则∠FDC的大小为_________. 90°7. 如图Z6-29是一枚“八一”建军节纪念章,其外轮廓是一个正五边形,则∠1的大小为__________°. 1088. 如图Z6-30,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=__________°. 425 三、解答题
9. 已知在一个十二边形中,其中十一个内角的和是 1 680°,求这个十二边形另一个内角的度数.
解:∵十二边形的内角和为(12-2)×180°=
1 800°,其中十一个内角的和是1 680°,
∴这个十二边形另一个内角的度数为1 800°-
1 680°=120°.
答:这个十二边形另一个内角的度数是120°.
10. 如图Z6-31,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么? 11. (1)一个多边形每个内角都相等,且每个外角等于一个内角的 ,求这个多边形的边数;
(2)两个多边形边数之比为3∶4,内角和之比为2∶3,求这两个多边形的边数. 解:(1)多边形的内角和是360°×1.5=540°.
设多边形的边数是n,
则(n-2)·180=540.
解得n=5.
答:这个多边形的边数是5.
(2)∵两个多边形的边数之比为3∶4,
∴设多边形的边数为3n,则另一个边数为4n.
∵内角和度数之比为2∶3,
∴(3n-2)∶(4n-2)=2∶3.
解得n=2.
∴3n=6, 4n=8.
答:这两个多边形的边数分别为6和8.
第六章 平行四边形
专题一 本章知识梳理
?思维导图?考纲要求1. 理解平行四边形的概念.
2. 探索并证明平行四边形的有关性质定理:平行四边形的对边相等、对角相等、对角线互相平分;探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
3. 探索并证明三角形中位线定理.
4. 探索并掌握多边形内角和与外角和公式.?知识梳理1. 平行四边形的定义、表示方法及有关概念
(1)________________的四边形叫做平行四边形.
(2)平行四边形_______的两个顶点连成的线段叫做它的对角线.
(3)如图Z6-1所示的四边形ABCD是平行四边形,记作“_______”,读作“_________________”,线段AC就是 的一条对角线.两组对边分别平行不相邻平行四边形ABCD?知识梳理2. 平行四边形的对称性
平行四边形是______对称图形,_________________是它的对称中心.
3. 多边形的内角和定理
(1)四边形可以被从同一个顶点出发的对角线分成_____个三角形,五边形可以被从同一个顶点出发的对角线分成_____个三角形……n边形可以被从同一个顶点出发的对角线分成________个三角形.
中心两条对角线的交点23(n-2)?知识梳理(2)多边形的内角和定理:n边形的内角和等于__________(n是大于或等于3的自然数).
4. 多边形的外角及外角和定理
(1)多边形内角的一边与另一边的__________所组成的角叫做这个多边形的外角.
(2)在多边形的每一个顶点处取这个多边形的一个________,它们的和叫做这个多边形的外角和.
(3)多边形的外角和定理:多边形的外角和都等于________. (n-2)·180°反向延长线外角360°专题二 本章易错点归总易错点1 不能正确选用平行四边形的判定方法而致错
在解题过程中,有时误用条件而导致判断出错,凭主观想象就判断一个四边形是平行四边形.
?易错点【例1】如图Z6-2,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF. 其中不能判定四边形DEBF是平行四边形的有( )
A. 0个
B. 1个
C. 2个
D. 3个 ?易错点易错提示:易出现对判定定理理解不透,想当然没有深入证明而出错.
?易错点正解:根据平行四边形的定义或判定定理逐一判断即可.
答案:B1. 能判定四边形ABCD为平行四边形的题设是( )
A. AB=AD,CB=CD
B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D
D. AB∥CD,AD=BC?学以致用B易错点2 考虑不周,导致错解或漏解
对几何图形判断错误, 忘记根据不同情况去分类解析,导致错解或漏解.
【例2】如图Z6-3,在 ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长. ?易错点易错提示:在 ABCD中,易得BC=AD=7,△ABE是等腰三角形,然后分别从BE=3或4去求解即可求得答案. 易出现考虑不全而造成漏解.
?易错点正解:∵在 ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,∴BC=AD=3+4=7,AD∥BC,AB=CD,∠1=∠2. ∴∠1=∠3. ∴∠2=∠3,∴AB=BE. 然后分别从BE=3或4去分析求解以免考虑不全而造成漏解. ①若BE=3,则AB=CD=3,此时四边形ABCD的周长为2×(3+7)=20;②若BE=4,则AB=CD=4,此时四边形ABCD的周长为2×(4+7)=22. ∴四边形ABCD的周长为20或22. ?易错点 2. 已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是_______________.?学以致用75°或15°专题三 本章重要考点专练——平行四边形的性质与判定一、选择题
1. 如图Z6-4,在 ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
A. 6
B. 12
C. 18
D. 24B2. 如图Z6-5,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A.
B. 2
C.
D. 4C3. 如图Z6-6,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
A. 1个
B. 2个
C. 3个
D. 4个D4. 如图Z6-7,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A. 2
B. 1
C.
D. B二、填空题
5. 已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=__________. 4或-26. 如图Z6-8,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F. 若∠EAF=56°,则∠B=______°. 567. 如图Z6-9,将 ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是__________. (7,4)三、解答题
8. 如图Z6-10,E是 ABCD的边AD的中点,连接CE并延长交BA的延长线于点F,若CD=6,求BF的长. 9. 如图Z6-11,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形. 10. 如图Z6-12,在 ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
求证:BC=BF. 11. 如图Z6-13,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF,BD,求证:四边形ABDF是平行四边形. 12. 如图Z6-14,在 ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°. 求∠B的度数. 专题四 本章重要考点专练——三角形的中位线一、选择题
1. 如图Z6-15,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为点D,OD=50 cm,当它的一端B着地时,另一端A离地面的高度AC为
( )
A. 25 cm
B. 50 cm
C. 75 cm
D. 100 cmD2. 如图Z6-16,点D,E,F分别为△ABC各边的中点,下列说法正确的是( )
A. DE=DF
B. EF= AB
C. S△ABD=S△ACD
D. AD平分∠BACC3. 如图Z6-17,在△ABC中,∠ABC=90°,AB=8,BC=6. 若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为
( )
A. 7
B. 8
C. 9
D. 10B4. 如图Z6-18,在△ABC中,AB=AC,点E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是
( )
A. ∠ECD=112.5°
B. DE平分∠FDC
C. ∠DEC=30°
D. AB= CDC二、填空题
5. 如图Z6-19,A,B两点被池塘隔开,不能直接测量其距离. 于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200 m,则A,B间的距离为__________m. 1006. 如图Z6-20,在Rt△ABC中,∠C=90°,BC=6,AC=8,点D,E分别为AC,AB的中点,连接DE,则△ADE的面积是_________. 67. 如图Z6-21,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=5,AC=3,则DF的长为________. 18. 如图Z6-22,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,…,如此操作下去,则第n个小三角形的
面积为__________. 三、解答题
9. 如图Z6-23,在△ABC中,CD是高,CE是中线,CE=CB,点A,D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE. 若AC=18,BC=12,求△CEG的周长. 10. 如图Z6-24,等边△ABC的边长是2,点D,E分别为AB,AC的中点,延长BC至点F,使CF= BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长. 11.如图Z6-25,四边形ABCD为平行四边形,点E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点. 判断CH与DG的位置关系,并说明理由. 12. 如图Z6-26,点M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长. 专题五 本章重要考点专练——多边形的内角和与外角和一、选择题
1. 若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A. 3 B. 4 C. 5 D. 6
2. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70AC3. 如图Z6-27,将图Z6-27①中五边形纸片ABCDE的A点以BE为折线往下折,A点恰好落在CD上,如图Z6-27②所示,再分别以图中的AB,AE为折线,将C,D两点往上折,使得A,B,C,D,E五点均在同一平面上,如图Z6-27③所示,若图Z6-27①中∠A=124°,则图Z6-27③中∠CAD的度数为何( )
A. 56°
B. 60°
C. 62°
D. 68°D二、填空题
4. 正八边形的每个外角的度数为__________.
5. 若多边形的每一个内角均为135°,则这个多边形的边数为__________. 45°86.如图Z6-28所示的正六边形ABCDEF,连接FD,则∠FDC的大小为_________. 90°7. 如图Z6-29是一枚“八一”建军节纪念章,其外轮廓是一个正五边形,则∠1的大小为__________°. 1088. 如图Z6-30,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=__________°. 425 三、解答题
9. 已知在一个十二边形中,其中十一个内角的和是 1 680°,求这个十二边形另一个内角的度数.
解:∵十二边形的内角和为(12-2)×180°=
1 800°,其中十一个内角的和是1 680°,
∴这个十二边形另一个内角的度数为1 800°-
1 680°=120°.
答:这个十二边形另一个内角的度数是120°.
10. 如图Z6-31,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么? 11. (1)一个多边形每个内角都相等,且每个外角等于一个内角的 ,求这个多边形的边数;
(2)两个多边形边数之比为3∶4,内角和之比为2∶3,求这两个多边形的边数. 解:(1)多边形的内角和是360°×1.5=540°.
设多边形的边数是n,
则(n-2)·180=540.
解得n=5.
答:这个多边形的边数是5.
(2)∵两个多边形的边数之比为3∶4,
∴设多边形的边数为3n,则另一个边数为4n.
∵内角和度数之比为2∶3,
∴(3n-2)∶(4n-2)=2∶3.
解得n=2.
∴3n=6, 4n=8.
答:这两个多边形的边数分别为6和8.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
