陕西省榆林二中2018-2019学年高二下学期期中考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省榆林二中2018-2019学年高二下学期期中考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 307.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-10 15:20:21 | ||
图片预览



文档简介
榆林市第二中学2018--2019学年第二学期期中考试
高二年级数学(理科)试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
用反证法证明命题:“已知a,b∈N,若ab可被5整除,则a,b中至少有一个能被5整除”时,反设正确的是( )
A. a,b都不能被5整除 B. a,b都能被5整除 C. a,b中有一个不能被5整除 D. a,b中有一个能被5整除
下列说法不正确的是( )
A. 综合法是由因导果的顺推证法 B. 分析法是执果索因的逆推证法 C. 分析法是从要证的结论出发,寻求使它成立的充分条件 D. 综合法与分析法在同一题的证明中不可能同时采用
若曲线在点处的切线方程是,则( )
A. B.
C. ? D.
函数y=ln(3x)的导数为()
A. B. C. D.
已知函数,则的值为(?? )
A. 10 B. C. D. 20
《易经》是中国传统文化中的精髓.如图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成(“”表示一根阳线,“”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有5根阳线和1根阴线的概率为( )
A. B. C. D.
在(1+x)2+(1+x)3+…+(1+x)9的展开式中,含x2项的系数是( )
A. 119 B. 120 C. 121 D. 720
二项式(x+1)8的展开式的各项系数和等于( )
A. 256 B. 257 C. 254 D. 255
已知P(B|A)=, P(A)=,则P(AB)等于( )
A. B. C. D.
某气象局在连续四天的天气预报中,至少一次预报准确的概率是,则该气象局一次天气预报准确的概率为(??? )
A. B. C. D.
已知研究x与y之间关系的一组数据如表所示:
x
0
1
2
3
4
y
1
3.5
5.5
7
8
则y对x的回归直线方程必过点(??? )
A. B. C. D.
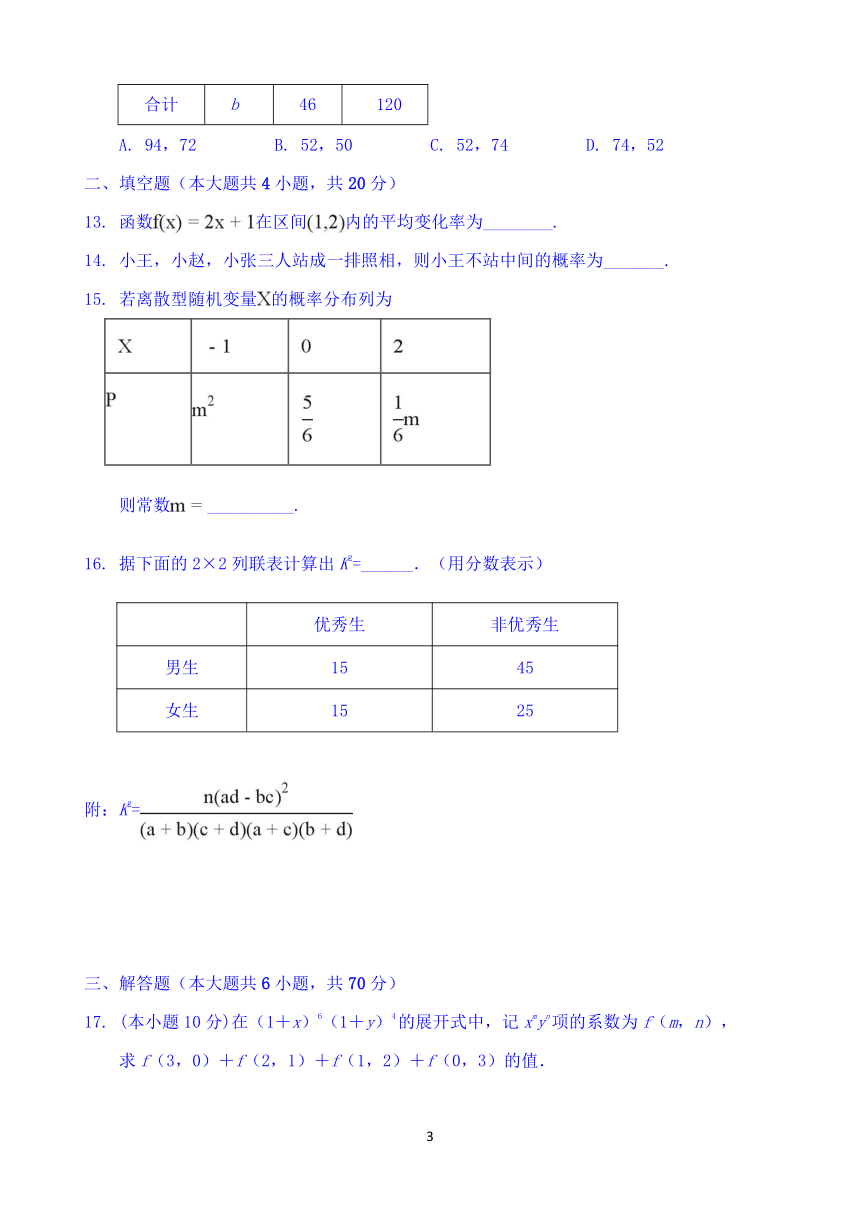
下面是2×2列联表,则表中a,b的值分别为( )
y1
y2
合计
x1
a
21
73
x2
22
25
47
合计
b
46
120
A. 94,72 B. 52,50 C. 52,74 D. 74,52
二、填空题(本大题共4小题,共20分)
函数在区间内的平均变化率为________.
小王,小赵,小张三人站成一排照相,则小王不站中间的概率为_______.
若离散型随机变量的概率分布列为
?
??
??
??
??
?
??
?
则常数__________.
据下面的2×2列联表计算出K2=______.(用分数表示)
优秀生
非优秀生
男生
15
45
女生
15
25
附:K2=
三、解答题(本大题共6小题,共70分)
(本小题10分)在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),
求f(3,0)+f(2,1)+f(1,2)+f(0,3)的值.
(本小题12分)已知?,Sn 为前n项和。
(1)计算
(2)猜想公式,并用数学归纳法证明
(本小题12分)已知是函数的导函数,求解下列问题.
(1)若,求的值;
(2)已知,求的表达式.
(本小题12分)某次文艺晚会上共演出7个节目,其中2个歌曲,3个舞蹈,2个曲艺节目,求分别满足下列条件的节自编排方法有多少种?(用数字作答) (1)一个歌曲节目开头,另个歌曲节目放在最后压台; (2)2个歌曲节目相邻且2个曲艺节目不相邻.
(本小题12分)已知函数.
(1)求曲线在点处的切线方程;
(2)直线为曲线的切线,且经过原点,求直线的方程及切点坐标.
(本小题12分)某同学理科成绩优异,今年参加了数学,物理,化学,生物4门学科竞赛.已知该同学数学获一等奖的概率为,物理,化学,生物获一等奖的概率都是,且四门学科是否获一等奖相互独立.
(1)求该同学至多有一门学科获得一等奖的概率;
(2)用随机变量X表示该同学获得一等奖的总数,求X的概率分布和数学期望.
高二理科数学答案
一、选择题(本大题共12小题,共60分)
1. A 2. D 3. A 4. C 5. C 6. A 7. B 8. A 9. C 10. D 11. B 12. C
二、填空题(本大题共4小题,共20分)
13. 2 14.15.? 16.
三、解答题(本大题共6小题,共70分)
17.(本题10分)解:(1+x)6(1+y)4的展开式中,含x3y0的系数是:C63C40=20.f(3,0)=20; 含x2y1的系数是C62C41=60,f(2,1)=60; 含x1y2的系数是C61C42=36,f(1,2)=36; 含x0y3的系数是C60C43=4,f(0,3)=4; ∴f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.
18.(本题12分)解:(1),
,;
(2)猜想:,
证明:①当n=1时,左边=,右边=,左边=右边,等式成立,
②假设当时等式成立,即
,
则:,
=,=,=,=,=,即当n=k+1时,猜想也成立,
根据①、②可知,猜想对任何都成立.
19. (本题12分)【答案】解:(1)∵, ∴ , ∴. (2)∵. ∴.
20. (本题12分)解:(1)根据题意,分2步进行分析: ①,要求2个歌曲节目1个在开头,另一个在最后,有A22=2种安排方法, ②,将剩下的5个节目全排列,安排在中间,有A55=120种安排方法, 则一共有2×120=240种安排方法; (2)根据题意,分3步进行分析: ①,2个歌曲节目相邻,将其看成一个整体,有A22=2种情况, ②,将这个整体与3个舞蹈节目全排列,有A44=24种情况,排好后有5个空位, ③,在5个空位中任选2个,安排2个曲艺节目,有A52=20种情况, 则一共有2×24×20=960种安排方法.
21. (本题12分)【解析】(Ⅰ),所以 ,即 (Ⅱ)设切点为,则 所以切线方程为 因为切线过原点,所以 , 所以,解得, 所以,故所求切线方程为, ?又因为,切点为
22. (本题12分)解:(1)记“该同学获得个一等奖”为事件,, 则,, 所以该同学至多有一门学科获得一等奖的概率为:. (2)随机变量的可能取值为0,1,2,3,4, ,, , ?, , 所以的概率分布为: ? 故.
高二年级数学(理科)试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
用反证法证明命题:“已知a,b∈N,若ab可被5整除,则a,b中至少有一个能被5整除”时,反设正确的是( )
A. a,b都不能被5整除 B. a,b都能被5整除 C. a,b中有一个不能被5整除 D. a,b中有一个能被5整除
下列说法不正确的是( )
A. 综合法是由因导果的顺推证法 B. 分析法是执果索因的逆推证法 C. 分析法是从要证的结论出发,寻求使它成立的充分条件 D. 综合法与分析法在同一题的证明中不可能同时采用
若曲线在点处的切线方程是,则( )
A. B.
C. ? D.
函数y=ln(3x)的导数为()
A. B. C. D.
已知函数,则的值为(?? )
A. 10 B. C. D. 20
《易经》是中国传统文化中的精髓.如图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成(“”表示一根阳线,“”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有5根阳线和1根阴线的概率为( )
A. B. C. D.
在(1+x)2+(1+x)3+…+(1+x)9的展开式中,含x2项的系数是( )
A. 119 B. 120 C. 121 D. 720
二项式(x+1)8的展开式的各项系数和等于( )
A. 256 B. 257 C. 254 D. 255
已知P(B|A)=, P(A)=,则P(AB)等于( )
A. B. C. D.
某气象局在连续四天的天气预报中,至少一次预报准确的概率是,则该气象局一次天气预报准确的概率为(??? )
A. B. C. D.
已知研究x与y之间关系的一组数据如表所示:
x
0
1
2
3
4
y
1
3.5
5.5
7
8
则y对x的回归直线方程必过点(??? )
A. B. C. D.
下面是2×2列联表,则表中a,b的值分别为( )
y1
y2
合计
x1
a
21
73
x2
22
25
47
合计
b
46
120
A. 94,72 B. 52,50 C. 52,74 D. 74,52
二、填空题(本大题共4小题,共20分)
函数在区间内的平均变化率为________.
小王,小赵,小张三人站成一排照相,则小王不站中间的概率为_______.
若离散型随机变量的概率分布列为
?
??
??
??
??
?
??
?
则常数__________.
据下面的2×2列联表计算出K2=______.(用分数表示)
优秀生
非优秀生
男生
15
45
女生
15
25
附:K2=
三、解答题(本大题共6小题,共70分)
(本小题10分)在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),
求f(3,0)+f(2,1)+f(1,2)+f(0,3)的值.
(本小题12分)已知?,Sn 为前n项和。
(1)计算
(2)猜想公式,并用数学归纳法证明
(本小题12分)已知是函数的导函数,求解下列问题.
(1)若,求的值;
(2)已知,求的表达式.
(本小题12分)某次文艺晚会上共演出7个节目,其中2个歌曲,3个舞蹈,2个曲艺节目,求分别满足下列条件的节自编排方法有多少种?(用数字作答) (1)一个歌曲节目开头,另个歌曲节目放在最后压台; (2)2个歌曲节目相邻且2个曲艺节目不相邻.
(本小题12分)已知函数.
(1)求曲线在点处的切线方程;
(2)直线为曲线的切线,且经过原点,求直线的方程及切点坐标.
(本小题12分)某同学理科成绩优异,今年参加了数学,物理,化学,生物4门学科竞赛.已知该同学数学获一等奖的概率为,物理,化学,生物获一等奖的概率都是,且四门学科是否获一等奖相互独立.
(1)求该同学至多有一门学科获得一等奖的概率;
(2)用随机变量X表示该同学获得一等奖的总数,求X的概率分布和数学期望.
高二理科数学答案
一、选择题(本大题共12小题,共60分)
1. A 2. D 3. A 4. C 5. C 6. A 7. B 8. A 9. C 10. D 11. B 12. C
二、填空题(本大题共4小题,共20分)
13. 2 14.15.? 16.
三、解答题(本大题共6小题,共70分)
17.(本题10分)解:(1+x)6(1+y)4的展开式中,含x3y0的系数是:C63C40=20.f(3,0)=20; 含x2y1的系数是C62C41=60,f(2,1)=60; 含x1y2的系数是C61C42=36,f(1,2)=36; 含x0y3的系数是C60C43=4,f(0,3)=4; ∴f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.
18.(本题12分)解:(1),
,;
(2)猜想:,
证明:①当n=1时,左边=,右边=,左边=右边,等式成立,
②假设当时等式成立,即
,
则:,
=,=,=,=,=,即当n=k+1时,猜想也成立,
根据①、②可知,猜想对任何都成立.
19. (本题12分)【答案】解:(1)∵, ∴ , ∴. (2)∵. ∴.
20. (本题12分)解:(1)根据题意,分2步进行分析: ①,要求2个歌曲节目1个在开头,另一个在最后,有A22=2种安排方法, ②,将剩下的5个节目全排列,安排在中间,有A55=120种安排方法, 则一共有2×120=240种安排方法; (2)根据题意,分3步进行分析: ①,2个歌曲节目相邻,将其看成一个整体,有A22=2种情况, ②,将这个整体与3个舞蹈节目全排列,有A44=24种情况,排好后有5个空位, ③,在5个空位中任选2个,安排2个曲艺节目,有A52=20种情况, 则一共有2×24×20=960种安排方法.
21. (本题12分)【解析】(Ⅰ),所以 ,即 (Ⅱ)设切点为,则 所以切线方程为 因为切线过原点,所以 , 所以,解得, 所以,故所求切线方程为, ?又因为,切点为
22. (本题12分)解:(1)记“该同学获得个一等奖”为事件,, 则,, 所以该同学至多有一门学科获得一等奖的概率为:. (2)随机变量的可能取值为0,1,2,3,4, ,, , ?, , 所以的概率分布为: ? 故.
同课章节目录
