3.1解决问题的策略(一) 课件(18张ppt)
文档属性
| 名称 | 3.1解决问题的策略(一) 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 727.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-11 00:00:00 | ||
图片预览






文档简介
课件18张PPT。解决问题的策略(1)苏教版六年级数学下册从三年级起,每一册数学都学习了一种策略,你们知道我们学了哪些策略?
学习目标:根据具体问题用转化的策略解决分数应用题
学习重点:合理的选择以前学过的策略来解决新的问题
今天,我们将学习运用画图转化的策略,解决一些以前学过的数学问题。《“画图 转化”的策略解决问题》例1.星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?1.这是一道什么应用题?2.根据“男生人数占总人数的 ”,可以知道什么?4.这是我们常见的分数应用题,除了用方程,你还会用其他方法吗?解:设星河小学美术组总人数为χ人。总人数-男生人数=女生人数χ - χ=21
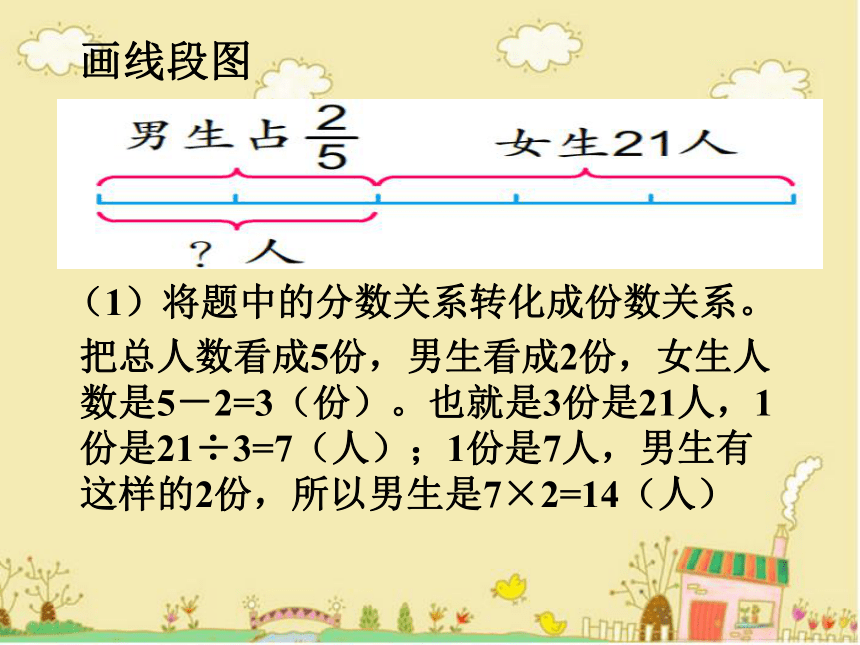
χ=35男生人数:35 - 21=14(人)画线段图(1)将题中的分数关系转化成份数关系。把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。列综合算式:检验:14÷(14+21)
=14÷35
=(2)将题中的分数关系转化成比的关系。男生人数占总人数的 。 男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,男生人数与女生人数的比是2 ︰3。男生人数与女生人数的比是2 ︰3。求一个数是另一个数的几分之几?用乘法计算。答:男生有14人。列式计算:总结
解决上面的问题,我们用了解方程的策略、画图的策略和把分数转化成比的策略,在这三种策略中,你觉得哪种策略更适合。解方程画图转化成比三种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。2.分数转化成比策略:更容易理解数量之间的关系。3.解方程策略:可以直观的将题目中的等量关系表现出来。 今天我们主要学习的是画图转化策略,只要画出图来,我们就能很快、很清楚的看出数量关系,列式解答。归纳总结 现在我们就用画图策略解决一些实际问题。练习五253523752725课堂总结 同学们,这节课你学习了哪些策略?主要学会了什么策略呢?学生作业:练习五第2、3题。53第一枝×(1- )=第二枝×(1- )
第一枝× =第二枝× =1
4
—
5 2
—
3 1
—
5 1
—
3第一枝:第二枝=5:3祝大家
χ=35男生人数:35 - 21=14(人)画线段图(1)将题中的分数关系转化成份数关系。把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。列综合算式:检验:14÷(14+21)
=14÷35
=(2)将题中的分数关系转化成比的关系。男生人数占总人数的 。 男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,男生人数与女生人数的比是2 ︰3。男生人数与女生人数的比是2 ︰3。求一个数是另一个数的几分之几?用乘法计算。答:男生有14人。列式计算:总结
解决上面的问题,我们用了解方程的策略、画图的策略和把分数转化成比的策略,在这三种策略中,你觉得哪种策略更适合。解方程画图转化成比三种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。2.分数转化成比策略:更容易理解数量之间的关系。3.解方程策略:可以直观的将题目中的等量关系表现出来。 今天我们主要学习的是画图转化策略,只要画出图来,我们就能很快、很清楚的看出数量关系,列式解答。归纳总结 现在我们就用画图策略解决一些实际问题。练习五253523752725课堂总结 同学们,这节课你学习了哪些策略?主要学会了什么策略呢?学生作业:练习五第2、3题。53第一枝×(1- )=第二枝×(1- )
第一枝× =第二枝× =1
4
—
5 2
—
3 1
—
5 1
—
3第一枝:第二枝=5:3祝大家
