7.2.2总复习 平面图形的认识(二) 课件(33张PPT)
文档属性
| 名称 | 7.2.2总复习 平面图形的认识(二) 课件(33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-11 00:00:00 | ||
图片预览



文档简介
课件33张PPT。小学数学总复习苏版六年级数学下册平面图形的认识教学目标1.使学生进一步掌握几何体的特征,发展学生的空间观念,加深对长方体、正方体和圆柱体的表面积的意义的认识。
2.运用分析、比较等方法,理解体积和容积的联系和区别。?
3运用立体图形表面积的知识解决一些简单的实际问题,丰富解决问题的策略。 导学提示
1、长方体的基本特征?正方体的基本特征?他们的相同点和不同点有哪些?
2、长方体和正方体的棱长、表面积、体积公式是什么?
3、?圆柱的侧面展开是什么形状?圆柱的侧面积。侧面展开的长方形的长、宽与圆柱有什么联系?
4、圆柱表面积怎么计算?圆柱的体积公式是什么?
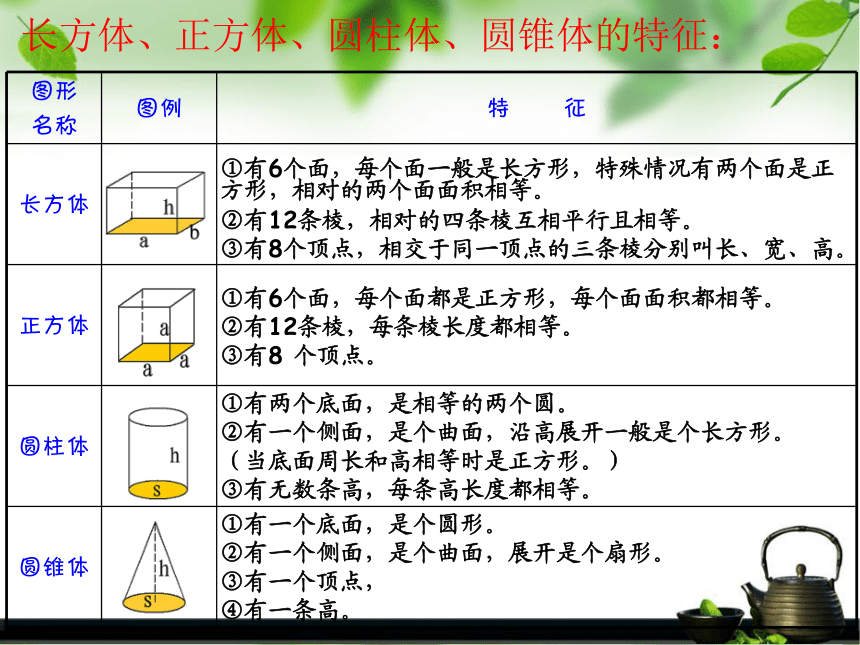
5、圆锥和圆柱有什么关系?圆锥的体积怎么求??长方体、正方体、圆柱体、圆锥体的特征:①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点,
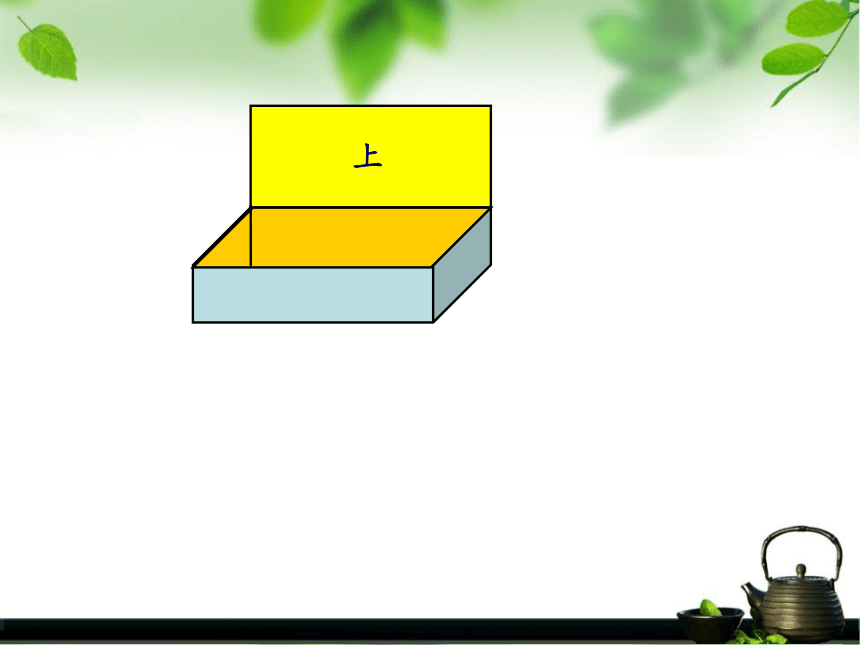
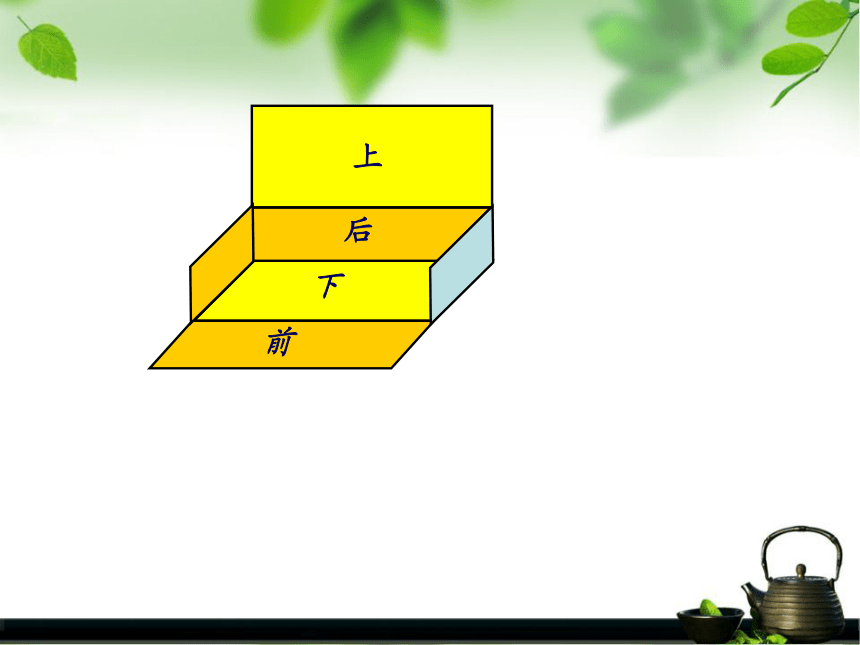
④有一条高。长方体的表面积:上上下前后上下前后左上下前后左右上下前后左右上下前后左右下前后上左右上下前后左右10厘米(长)6厘米(宽)2厘米(高) (0.7×0.5+0.7×0.4+0.5×0.4)×2 0.7×0.5×2+0.7×0.4×2+0.5×0.4×2上和下前和后右和左长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2上(或下)前(或后)右(或左)长方体的表面积=(长×宽+长×高+高×宽)× 2正方体的表面积:上下前后左右正方体的表面积=棱长×棱长×6或=棱长2×66分米6分米6分米62×6长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高V=abh长方体的体积=底面积×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积=底面积×高正方体的体积:底面底面侧面圆柱的表面积 =两个底面的面积+圆柱的侧面积 S表=2S底+S侧圆柱的表面积:圆柱的侧面积怎样计算呢?底面底面底面的周长高侧面圆柱的侧面积 = 底面周长 × 高S侧=Ch长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。因为 V圆柱=Sh圆锥的体积:长方体、正方体、圆柱体、圆锥体的相关计算:4a+4b+4h
或4(a+b+c)S长=2ab+2ah+2bh
=(ab+ah+bh)×2S正=a2×6S表=2S底+S侧
S侧=Ch
S表=C(r+h)V长=abh12aV正=a3 V柱=ShV=Sh导学提示(二)
1.?复习体积(容积)的意义。? 什么是物体的体积?什么是物体的容积?体积和容积之间有什么联系和区别??
2.?复习体积(容积单位)。? 提问:常用的体积(容积)单位有哪些?(立方米、立方分米、立方厘米、升、毫升)? 你能说一说相邻单位之间的进率吗??盒子的体积与盒子的容积哪个大 ?仔细观察: 对于同一个容器,它的体积一定比容积大,因为它有厚度。物体的容积: 容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。表面积、体积、容积的对比:物体表面面积的总和(所有面面积的总和)物体所占空间的大小容器所能容纳物体体积的大小m2 dm2 cm2m3 dm3 cm3m3 dm3 cm3
L ml1m2=100dm2
1dm2=100cm21m3=1000dm3
1dm3=1000cm31L=1000ml
1dm3=1L
1cm3=1ml练习√× 判断: × × × 6、计算圆柱形油桶能装多少升油就是求这个油桶
的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩
大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一
定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积。( )√× √× 判断: 10、体积单位间的进率都是1000 。 ( )
11、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
12、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
13、冰箱的容积就是冰箱的体积( )
14、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
15、一个油桶能装多少升油,就是求它的容积。( )×√× 判断: ×√√回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 谈 收 获
2.运用分析、比较等方法,理解体积和容积的联系和区别。?
3运用立体图形表面积的知识解决一些简单的实际问题,丰富解决问题的策略。 导学提示
1、长方体的基本特征?正方体的基本特征?他们的相同点和不同点有哪些?
2、长方体和正方体的棱长、表面积、体积公式是什么?
3、?圆柱的侧面展开是什么形状?圆柱的侧面积。侧面展开的长方形的长、宽与圆柱有什么联系?
4、圆柱表面积怎么计算?圆柱的体积公式是什么?
5、圆锥和圆柱有什么关系?圆锥的体积怎么求??长方体、正方体、圆柱体、圆锥体的特征:①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点,
④有一条高。长方体的表面积:上上下前后上下前后左上下前后左右上下前后左右上下前后左右下前后上左右上下前后左右10厘米(长)6厘米(宽)2厘米(高) (0.7×0.5+0.7×0.4+0.5×0.4)×2 0.7×0.5×2+0.7×0.4×2+0.5×0.4×2上和下前和后右和左长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2上(或下)前(或后)右(或左)长方体的表面积=(长×宽+长×高+高×宽)× 2正方体的表面积:上下前后左右正方体的表面积=棱长×棱长×6或=棱长2×66分米6分米6分米62×6长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高V=abh长方体的体积=底面积×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积=底面积×高正方体的体积:底面底面侧面圆柱的表面积 =两个底面的面积+圆柱的侧面积 S表=2S底+S侧圆柱的表面积:圆柱的侧面积怎样计算呢?底面底面底面的周长高侧面圆柱的侧面积 = 底面周长 × 高S侧=Ch长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。因为 V圆柱=Sh圆锥的体积:长方体、正方体、圆柱体、圆锥体的相关计算:4a+4b+4h
或4(a+b+c)S长=2ab+2ah+2bh
=(ab+ah+bh)×2S正=a2×6S表=2S底+S侧
S侧=Ch
S表=C(r+h)V长=abh12aV正=a3 V柱=ShV=Sh导学提示(二)
1.?复习体积(容积)的意义。? 什么是物体的体积?什么是物体的容积?体积和容积之间有什么联系和区别??
2.?复习体积(容积单位)。? 提问:常用的体积(容积)单位有哪些?(立方米、立方分米、立方厘米、升、毫升)? 你能说一说相邻单位之间的进率吗??盒子的体积与盒子的容积哪个大 ?仔细观察: 对于同一个容器,它的体积一定比容积大,因为它有厚度。物体的容积: 容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。表面积、体积、容积的对比:物体表面面积的总和(所有面面积的总和)物体所占空间的大小容器所能容纳物体体积的大小m2 dm2 cm2m3 dm3 cm3m3 dm3 cm3
L ml1m2=100dm2
1dm2=100cm21m3=1000dm3
1dm3=1000cm31L=1000ml
1dm3=1L
1cm3=1ml练习√× 判断: × × × 6、计算圆柱形油桶能装多少升油就是求这个油桶
的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩
大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一
定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积。( )√× √× 判断: 10、体积单位间的进率都是1000 。 ( )
11、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
12、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
13、冰箱的容积就是冰箱的体积( )
14、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
15、一个油桶能装多少升油,就是求它的容积。( )×√× 判断: ×√√回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 谈 收 获
