人教版七年级数学下册5.2.1平行线课件(31张)
文档属性
| 名称 | 人教版七年级数学下册5.2.1平行线课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-10 21:15:37 | ||
图片预览











文档简介
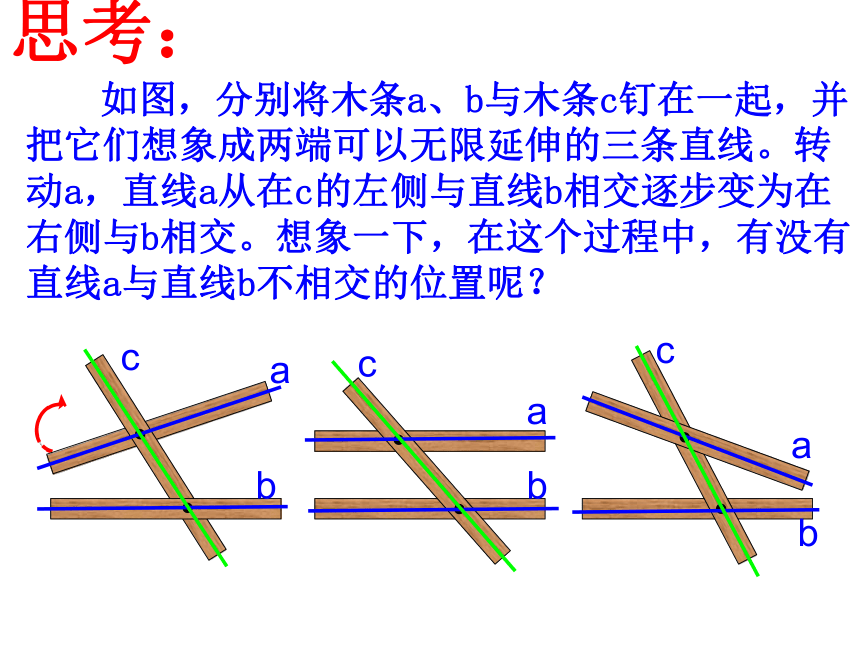
课件31张PPT。5.2.1 平行线 如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线。转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?思考: 在木条转动过程中,存在一个直线a与直线b不相交的位置,这时我们说直线a与b互相平行。 平行线在生活中是很常见的,你还
能举出其他一些例子吗?短池游泳双杠扶梯高速公路zxxk1、平行线的定义: 在同一平面内,不相交的两条直线叫平行线.1、在同 一平面内平行线有什么特征?2、不相交平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有
交点,
(3)平行线指的是“两条直线”而不
是两条射线或两条线段.注意: 如何用几何语言描述平行呢?2、平行线的表示方法:平行用符号“∥”表示,
如:直线AB与直线CD平行,
记作:AB∥CD,读作“AB平行于CD”。注意:平行线是相互的,使用平行符号“∥”时,可写成AB∥CD,也可以写成:
CD∥AB。如果用a、b表示这两条直线,那么直线a与直线b平行,记作:a∥b.也可以写成: b ∥ a 。 在同一平面内,两条直线有几种位置关系?动手画一画?学科网同一平面内两直线的位置关系:平行相交垂直相交但不垂直a⊥ba ∥b结论:在同一平面内,两直线的位置
关系有平行与相交两种。(1)你能在右图中的方格中画出
平行线吗?方法:①利用方格纸中的直线画平行线。②利用格点(长方形的对角线)画平行线。试一试(2)若改方格纸为白纸,你能利用以下哪些工具:
①直尺 ②三角板 ③量角器
画已知直线AB的平行线?能画多少条?已知直线AB,画一条直线和已知直线AB平行AB若将此处的直角改为锐角将会怎样?3、平行线的画法:“推平行线法”: zxxk一、放二、靠三、推四、画“推平行线法”: BA平行线的画法:●一放二靠三推四画 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。PBA学科网一、放二、靠三、推四、画●PBA 一般地,经过直线外一点,有且只有一条直线与这条直线平行。结论:说明:人们在长期实践中总结出来的结论叫基本
事实,也称为公理,它可以作为以后推理的依据.
平行线的性质(平行公理) (1)经过点A画出直线n的平行线,能画几条? (2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗? 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。··ABn平行线的传递性 (平行公理的推论):结论:几何语言表达式:∵a∥n m∥n(已知)
∴a∥m (平行线的传递性)ma探究新知你学会了吗?1、在同一个平面内, 的两条直线叫做平行线.
则在同一个平面内两条直线的位置关系是 .不相交相交或平行AB∥ CD,AD∥ BC。AB实践应用P 如图,在⊿ ABC中,P是AC边上一点.过点P分别画AB,BC的平行线.CDABP 如图,中,P是AC边上一点.过点P分别画AB,BC的在⊿ ABC平行线.cDE实践应用∴PD、PE就是所要画的直线。 1.同一平面内,三条直线的交点可以有 个. 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交0或1或2或3 3、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行 4.画∠AOB,在OB上取一点C,过点C画CD平行于OA,在OA上任取一点E,过点E画EF∥OB交CD于F,分别量得∠AOB、∠EFC,可得:___________;再测量∠AOB和∠OEF,可得__________________.DF∠AOB=∠EFC∠AOB+∠OEF=180° 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。平行线:在同一平面内,不相交的两条
直线叫做平行线。平行线的画法:
1、借助方格纸画;
2、借助三角尺画。
(一放、二靠、三推、四画)平行线的表示方法: m//n AB//CD平行线的性质:(平行公理) 经过直线外一点,有且只有一条直线与这条直线平行; 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。平行线的传递性 (平行公理的推论):归纳小结? 只有一个公共点的两条直线同一个平面内不相交的两条直线对顶角相等平行公理邻补角互补平行公理推论:
∵ a ∥ c,b ∥ c ;
∴ a ∥ b学科网
能举出其他一些例子吗?短池游泳双杠扶梯高速公路zxxk1、平行线的定义: 在同一平面内,不相交的两条直线叫平行线.1、在同 一平面内平行线有什么特征?2、不相交平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有
交点,
(3)平行线指的是“两条直线”而不
是两条射线或两条线段.注意: 如何用几何语言描述平行呢?2、平行线的表示方法:平行用符号“∥”表示,
如:直线AB与直线CD平行,
记作:AB∥CD,读作“AB平行于CD”。注意:平行线是相互的,使用平行符号“∥”时,可写成AB∥CD,也可以写成:
CD∥AB。如果用a、b表示这两条直线,那么直线a与直线b平行,记作:a∥b.也可以写成: b ∥ a 。 在同一平面内,两条直线有几种位置关系?动手画一画?学科网同一平面内两直线的位置关系:平行相交垂直相交但不垂直a⊥ba ∥b结论:在同一平面内,两直线的位置
关系有平行与相交两种。(1)你能在右图中的方格中画出
平行线吗?方法:①利用方格纸中的直线画平行线。②利用格点(长方形的对角线)画平行线。试一试(2)若改方格纸为白纸,你能利用以下哪些工具:
①直尺 ②三角板 ③量角器
画已知直线AB的平行线?能画多少条?已知直线AB,画一条直线和已知直线AB平行AB若将此处的直角改为锐角将会怎样?3、平行线的画法:“推平行线法”: zxxk一、放二、靠三、推四、画“推平行线法”: BA平行线的画法:●一放二靠三推四画 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。PBA学科网一、放二、靠三、推四、画●PBA 一般地,经过直线外一点,有且只有一条直线与这条直线平行。结论:说明:人们在长期实践中总结出来的结论叫基本
事实,也称为公理,它可以作为以后推理的依据.
平行线的性质(平行公理) (1)经过点A画出直线n的平行线,能画几条? (2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗? 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。··ABn平行线的传递性 (平行公理的推论):结论:几何语言表达式:∵a∥n m∥n(已知)
∴a∥m (平行线的传递性)ma探究新知你学会了吗?1、在同一个平面内, 的两条直线叫做平行线.
则在同一个平面内两条直线的位置关系是 .不相交相交或平行AB∥ CD,AD∥ BC。AB实践应用P 如图,在⊿ ABC中,P是AC边上一点.过点P分别画AB,BC的平行线.CDABP 如图,中,P是AC边上一点.过点P分别画AB,BC的在⊿ ABC平行线.cDE实践应用∴PD、PE就是所要画的直线。 1.同一平面内,三条直线的交点可以有 个. 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交0或1或2或3 3、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行 4.画∠AOB,在OB上取一点C,过点C画CD平行于OA,在OA上任取一点E,过点E画EF∥OB交CD于F,分别量得∠AOB、∠EFC,可得:___________;再测量∠AOB和∠OEF,可得__________________.DF∠AOB=∠EFC∠AOB+∠OEF=180° 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。平行线:在同一平面内,不相交的两条
直线叫做平行线。平行线的画法:
1、借助方格纸画;
2、借助三角尺画。
(一放、二靠、三推、四画)平行线的表示方法: m//n AB//CD平行线的性质:(平行公理) 经过直线外一点,有且只有一条直线与这条直线平行; 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。平行线的传递性 (平行公理的推论):归纳小结? 只有一个公共点的两条直线同一个平面内不相交的两条直线对顶角相等平行公理邻补角互补平行公理推论:
∵ a ∥ c,b ∥ c ;
∴ a ∥ b学科网
