7.2.7总复习 立体图形的表面积和体积(二)课件 (共27张PPT)
文档属性
| 名称 | 7.2.7总复习 立体图形的表面积和体积(二)课件 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 473.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-12 16:09:39 | ||
图片预览




文档简介
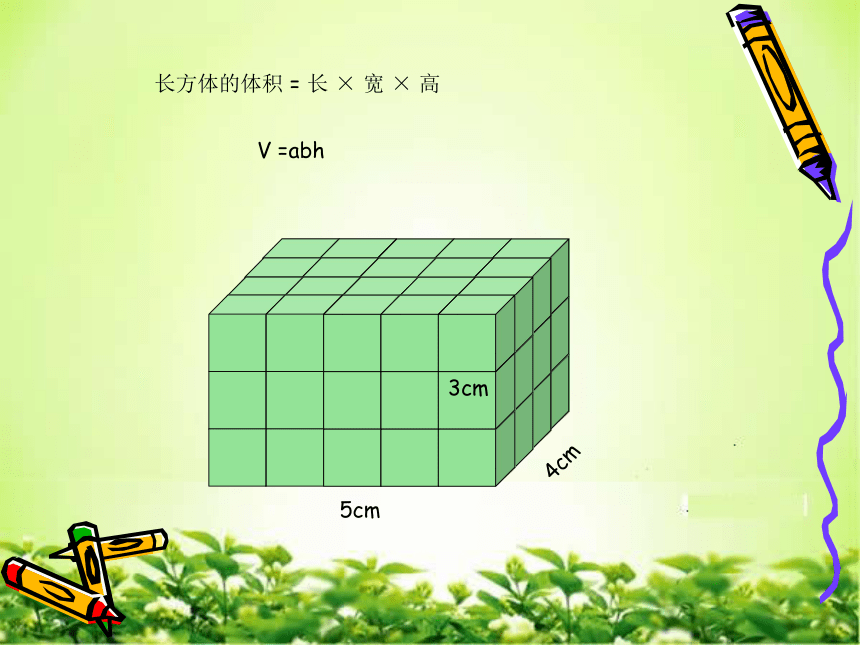
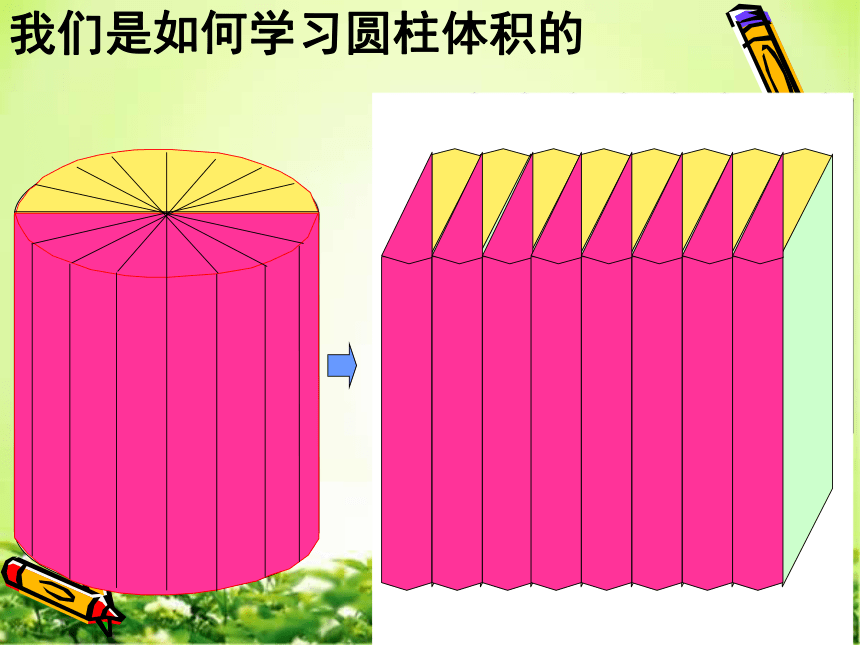
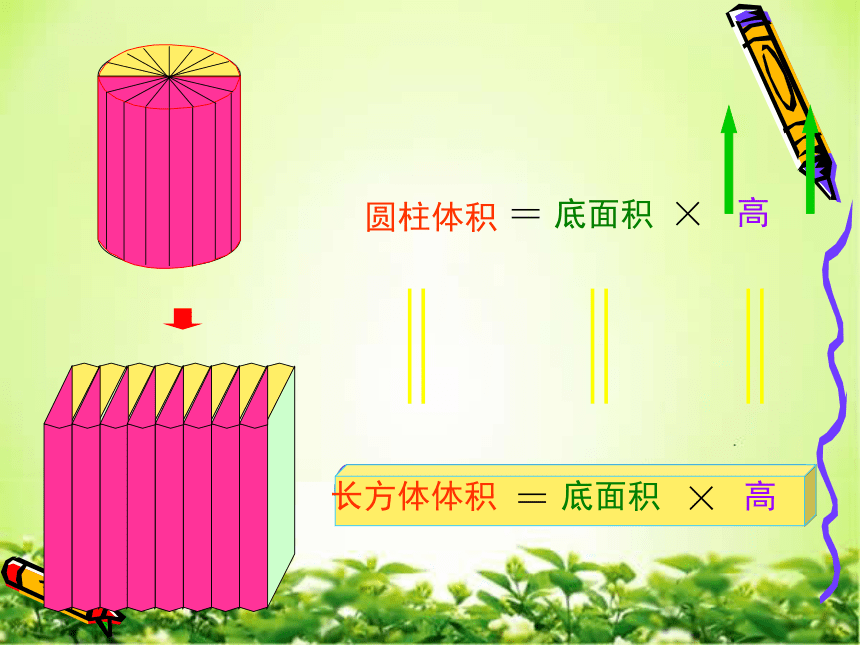
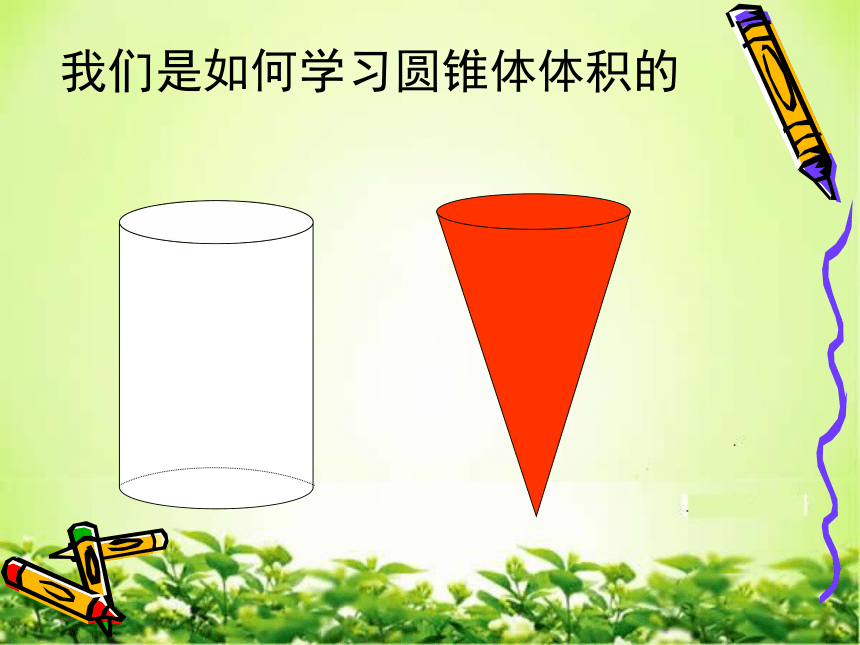
课件27张PPT。立体图形的表面积和体积5cm4cm3cm长方体的体积 = 长 × 宽 × 高 V =abh3cm3cm4cm3cm3cm3cm正方体的体积 = 棱长 × 棱长 × 棱长 V =a3我们是如何学习圆柱体积的体积底面积高公式圆柱体积长方体体积底面积底面积高高=×=×我们是如何学习圆锥体体积的结论:圆柱体积是等底等高 圆锥体积的3倍 ,圆锥体积是等底等高圆柱体积的
稳打稳算:
1、概念的判别
做一个长14厘米、宽8厘米、高6厘米的长方体框架,一共要用多少长的铁丝是求它的( )。把它全部糊起来,一共要多少平方厘米的硬纸板是求它的( )。这个长方体占多少空间,是求它的( )。这个纸盒能装多少粉笔,是求它的( )。棱长总和表面积 体积容积稳打稳算:
2、在括号里填上合适的单位名称
(1)一间卧室地面的面积是15( )
(2)一瓶牛奶大约有250( )
(3)我们教室的空间大约有144( )平方米毫升立方米稳打稳算:(只要列综合算式,不必计算)
3、制作下面的物体,至少各需要多少铁皮或玻璃?
油桶鱼缸通风管底面r=4 dm a=5 dm 横截面C=0.628 m
h=12 dm b=3 dm h=1.2 m
h=3.5 dm0.628 ×1.2×4 ×2 ×12 +×42×2(5 ×3.5 +3 ×3.5) ×2 +5 ×3
稳打稳算:
4、表面积的变化(列式计算)
(1)把一根长20分米,底面直径6分米的圆柱形木料锯成2段,表面积增加多少?锯成3段呢,表面积增加多少?×32×2=18(平方分米)×32×4=36(平方分米)
稳打稳算:
表面积的变化(列式计算)
(2)把一跟长20分米的圆柱形木料锯成4段,表面积增加了30平方分米,则这根木料原来的的体积是多少?
30÷6×20=100(立方分米)答:这根木料原来的的体积100立方分米。
稳打稳算:
表面积的变化(列式计算)
(3)把一根长2米,底面直径6分米的圆柱形木料沿底面直径切成两半后,表面积增加多少?6×20×2=240(平方分米)答:表面积增加240平方分米。稳操胜算:
1、一个圆柱形水池,底面直径是20米,深2米,水池的占地面积是多少平方米?
(1)在水池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米? (2)池内最多能蓄水多少吨?(每立方米水重1吨)×102=100(平方米)×20×2+×102=140(平方米)×102×2×1=200(吨)稳操胜算:
1、一个圆柱形水池,底面直径是20米,深2米。
(3)当注入的水深是1米时,工人师傅拿来一个正方体形状的铁块把它完全浸没在水中,此时水面上升到1.5米,你能求出正方体铁块的体积吗?
×102×(2 -1.5)=50(立方米)答:正方体铁块的体积是50 立方米。稳操胜算:
2、一个圆锥形沙堆,底面积是9平方米,高为1.2米。把它填入长5米,宽1.8米的长方体沙坑里。能填40厘米厚的沙吗?
9×1.2×1.8 ×5=9
3.6 ÷9=0.4(米)
0.4米=40(厘米)=3.6答:能填40厘米厚的沙。巧思秒算
如图,一个酒瓶身呈圆柱形,深30厘米,底内直径是10厘米,瓶里酒深15厘米.把酒瓶塞紧后使其瓶口向下倒立,这时酒深25厘米,问:酒瓶容积是多少?
数量关系:第一个酒瓶里的酒+第二个酒瓶里空白部分=整个酒瓶的容积
稳打稳算:
1、概念的判别
做一个长14厘米、宽8厘米、高6厘米的长方体框架,一共要用多少长的铁丝是求它的( )。把它全部糊起来,一共要多少平方厘米的硬纸板是求它的( )。这个长方体占多少空间,是求它的( )。这个纸盒能装多少粉笔,是求它的( )。棱长总和表面积 体积容积稳打稳算:
2、在括号里填上合适的单位名称
(1)一间卧室地面的面积是15( )
(2)一瓶牛奶大约有250( )
(3)我们教室的空间大约有144( )平方米毫升立方米稳打稳算:(只要列综合算式,不必计算)
3、制作下面的物体,至少各需要多少铁皮或玻璃?
油桶鱼缸通风管底面r=4 dm a=5 dm 横截面C=0.628 m
h=12 dm b=3 dm h=1.2 m
h=3.5 dm0.628 ×1.2×4 ×2 ×12 +×42×2(5 ×3.5 +3 ×3.5) ×2 +5 ×3
稳打稳算:
4、表面积的变化(列式计算)
(1)把一根长20分米,底面直径6分米的圆柱形木料锯成2段,表面积增加多少?锯成3段呢,表面积增加多少?×32×2=18(平方分米)×32×4=36(平方分米)
稳打稳算:
表面积的变化(列式计算)
(2)把一跟长20分米的圆柱形木料锯成4段,表面积增加了30平方分米,则这根木料原来的的体积是多少?
30÷6×20=100(立方分米)答:这根木料原来的的体积100立方分米。
稳打稳算:
表面积的变化(列式计算)
(3)把一根长2米,底面直径6分米的圆柱形木料沿底面直径切成两半后,表面积增加多少?6×20×2=240(平方分米)答:表面积增加240平方分米。稳操胜算:
1、一个圆柱形水池,底面直径是20米,深2米,水池的占地面积是多少平方米?
(1)在水池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米? (2)池内最多能蓄水多少吨?(每立方米水重1吨)×102=100(平方米)×20×2+×102=140(平方米)×102×2×1=200(吨)稳操胜算:
1、一个圆柱形水池,底面直径是20米,深2米。
(3)当注入的水深是1米时,工人师傅拿来一个正方体形状的铁块把它完全浸没在水中,此时水面上升到1.5米,你能求出正方体铁块的体积吗?
×102×(2 -1.5)=50(立方米)答:正方体铁块的体积是50 立方米。稳操胜算:
2、一个圆锥形沙堆,底面积是9平方米,高为1.2米。把它填入长5米,宽1.8米的长方体沙坑里。能填40厘米厚的沙吗?
9×1.2×1.8 ×5=9
3.6 ÷9=0.4(米)
0.4米=40(厘米)=3.6答:能填40厘米厚的沙。巧思秒算
如图,一个酒瓶身呈圆柱形,深30厘米,底内直径是10厘米,瓶里酒深15厘米.把酒瓶塞紧后使其瓶口向下倒立,这时酒深25厘米,问:酒瓶容积是多少?
数量关系:第一个酒瓶里的酒+第二个酒瓶里空白部分=整个酒瓶的容积
