5.5 递归算法实例及程序实现(27张幻灯片)
文档属性
| 名称 | 5.5 递归算法实例及程序实现(27张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2019-05-12 00:00:00 | ||
图片预览








文档简介
课件27张PPT。递归算法1、递归现象从前有座山,山里有座庙,庙里有个和尚,和尚在讲故事。
从前有座山,山里有座庙,庙里有个和尚,和尚在讲故事。
从前有座山,山里有座庙,庙里有个和尚,和尚在讲故事。
从前有座山…例子1:例子2:两面镜子中间的你,产生“像中像” ?
德罗斯特效应(Droste effect) 例子3: 《礼记·大学》:
古之欲明明德于天下者,先治其国;欲治其国者,先齐其家;欲齐其家者,先修其身;欲修其身者,先正其心;欲正其心者,先诚其意;欲诚其意者,先致其知,致知在格物。物格而后知至,知至而后意诚,意诚而后心正,心正而后身修,身修而后家齐,家齐而后国治,国治而后天下平。美德彰明于天下治理好国家整顿好家自我修养修身齐家治国平天下思想端正思想端正例子4: 为了解释一个词,需要使用更多的词。
当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查第二个词,可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。。。
例子1、2都是抽象出来的递归现象,但是严格来说并不是递归,因为会一直重复下去,没有终止条件,违背算法的“有穷性”。
例3和例4有终止条件
例3中思想端正
例4中最后完全看懂的词
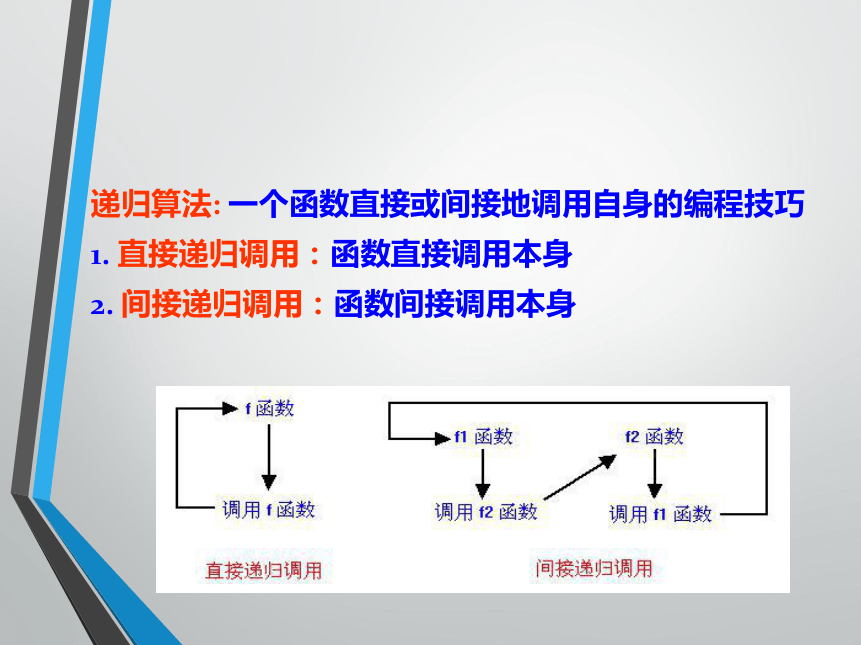
2、递归算法递归算法: 一个函数直接或间接地调用自身的编程技巧
1. 直接递归调用:函数直接调用本身
2. 间接递归调用:函数间接调用本身
直接递归调用和尚讲故事:故事包含故事,故事都是同一故事程序设计中,函数A自己调用自己,称为直接递归调用。镜子A和镜子B相对放在一起,你会发现什么现象呢?对了,我们会发现镜子A中有镜子B的映象,镜子B中又镜子A的映象,这样层层叠叠,无穷无尽。AB在程序设计中,像这种函数A调用函数B,函数B再反过来调用函数A的算法,称为间接递归调用。间接递归调用
递归算法是语言设计中的一种重要方法,只需少量的程序就可描述出解题过程,但是递归执行的过程比较复杂。
递归算法关键:
1.递归关系 2.递归终止条件
递归实例1设计一个vb程序,
输入正整数n,求出n的阶乘
5!=5*4*3*2*1=5*4!
4!=4*3*2*1=4*3!
3!=3*2*1=3*2!
2!=2*1=2*1!
1!=1
1:对于任意一个整数n (n>1):
n!=n*(n-1)!
2:终止条件 n=1
1!=1‘1、终止条件:n=1 时jc(1)=1
‘2、对于任意n>1找出jc(n)和jc(n-1)之间的关系n!=n*(n-1)!Function jc(n as integer) as integer
If n =1 then
jc(1)=1
else
jc(n) =n*jc(n-1)
End if
End functionjc=1jc= n*jc(n-1)递归函数的调用Function jc(byval n as integer) as integer
If n =1 then
jc=1
else
jc=n*jc(n-1)
End if
End Function
Private Sub Command1_Click()
a = Val(Text1.Text)
b = jc(a)
Label1.Caption = str(a)+“的阶乘为:”Str(b)
End Subjc(3)
=3*jc(2)jc(2)
=2*jc(1)jc(1)=1=2*1
=2=3*2
=6返回返回jc(3)
=3*jc(2)返回返回jc(3)
=3*jc(2)返回返回当n=3时y=jc(3)递归算法的基本思想是把规模较大的、较难解决的问题变成规模较小的、容易解决的同一问题,规模较小的问题又变成规模更小的问题,当问题小到一定程度时,可以直接得出它的解,从而得到原来问题的解。
即采用“大事化小、小事化了”的基本思想。jc=3*jc(2)jc=2*jc(1)jc=1递归实例2有5个人坐在一起,问第5个人多少岁,他说比第4个人大2岁;问第4个人岁数,他说比第3个人大2岁;问第3个人,又说比第2个大2岁;问第2个人,说比第1个人大2岁;最后问第1个人,他说他10岁;请问第5个人多大?
终止条件:第一个人10岁
递归关系:每一个人的年龄都比其前1个人的年龄大
age(5)=age(4)+2
age(4)=age(3)+2
age(3)=age (2)+2
age(2)=age(1)+2
age(1)=10
Function age (n as Integer)as Integer
If then
age =________
Else
age=___________
End if
End Functionn=110age(n-1)+2习题1:斐波那契数列问题斐波那契数列,又称黄金分割数列,指的是这样一个数列:
1、1、2、3、5、8、13、21、34、55……
这个数列从第3项开始,每一项都等于前两项之和。
设计一个VB程序
求:数列中的第n项是多少?
1、终止条件:最初两项值为1
2、递归关系:第n项的值是它之前两项之和 ( n大于3 )
求第N个斐波纳切数
if 前两项 then
斐波纳切数=1
else
斐波纳切数=前两个斐波纳切数之和
end ifFunction Fib (n as Integer)as Integer
If then
Fib =__
Else
Fib =__________________
End if
End Functionn<31Fib (n-2)+Fib (n-1)习题2:小猴吃桃问题有一天小猴子摘若干个桃子,当即吃了一半还觉得不过瘾,又多吃了一个。第二天接着吃剩下桃子中的一半,仍觉得不过瘾又多吃了一个,以后小猴子都是吃尚存桃子一半多一个。到第10天早上小猴子再去吃桃子的时候,看到只剩下一个桃子。问小猴子第一天共摘下了多少个桃子?
递归算法描述:
??? Function 你有多少桃子?(第几天)
?? If Then
? Else
End if
??? End Function桃子数=第n天的桃子数第n+1天的桃子数 2-1=第n天的桃子数=(第n+1天的桃子数+1)*2( 明天的桃子数+1)*2第10天 桃子数=1算法实现:
Function Tao(days As Integer) As Integer
If days = 10 Then
Tao = 1
Else
Tao = (Tao(days + 1) + 1) * 2
End If
End FunctionTao(1)=(Tao(2)+1)*2Tao(2)=(Tao(3)+1)*2Tao(3)=(Tao(4)+1)*2 Tao(8)=(Tao(9)+1)*2Tao(9)=(Tao(10)+1)*2Tao(10)= 1调用调用调用调用调用返回返回返回返回返回习题3:求最大公约数早在公元前300年左右,欧几里得就在他的著作《几何原本》中给出了高效的解法——辗转相除法。
辗转相除法的方法是用较大的数X除以较小的数Y,得到余数Z
如果余数为0,则较小数Y就是两者的最大公约数。
例如:27和9的最大公约数就是9
如果余数不为0,则较小数Y与余数Z的最大公约数就是X与Y的的
最大公约数
例如:140和63 的最大公约数就是63与14的最大公约数,
63与14的最大公约数就是14和7
14和7的最大公约数7
Function GYS(x as Integer,y as Integer)as Integer
Dim z as Integer
z=
If then
GYS=
Else
GYS=
End if
End Function求X与Y的公约数:
Z是X除Y得到的余数
If then
公约数=
Else
公约数=
End if YY 和 Z的公约数Z为0 X mod YZ=0YGYS( Y , Z )3、课堂小结递归算法实现的要点递归调用必须是有限制的,有限才有意义。构成递归的必须满足以下条件:
(1)有明确的结束递归的边界条件(又称终止条件)以及结束时的边界值;通过条件语句(If语句)来实现
(2)函数的描述中包含其本身,即能用递归形式表示Function jc(n as integer) as integer
If n =1 then
jc=1
else
jc=n*jc(n-1)
End if
End fun_ction
从前有座山,山里有座庙,庙里有个和尚,和尚在讲故事。
从前有座山,山里有座庙,庙里有个和尚,和尚在讲故事。
从前有座山…例子1:例子2:两面镜子中间的你,产生“像中像” ?
德罗斯特效应(Droste effect) 例子3: 《礼记·大学》:
古之欲明明德于天下者,先治其国;欲治其国者,先齐其家;欲齐其家者,先修其身;欲修其身者,先正其心;欲正其心者,先诚其意;欲诚其意者,先致其知,致知在格物。物格而后知至,知至而后意诚,意诚而后心正,心正而后身修,身修而后家齐,家齐而后国治,国治而后天下平。美德彰明于天下治理好国家整顿好家自我修养修身齐家治国平天下思想端正思想端正例子4: 为了解释一个词,需要使用更多的词。
当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查第二个词,可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。。。
例子1、2都是抽象出来的递归现象,但是严格来说并不是递归,因为会一直重复下去,没有终止条件,违背算法的“有穷性”。
例3和例4有终止条件
例3中思想端正
例4中最后完全看懂的词
2、递归算法递归算法: 一个函数直接或间接地调用自身的编程技巧
1. 直接递归调用:函数直接调用本身
2. 间接递归调用:函数间接调用本身
直接递归调用和尚讲故事:故事包含故事,故事都是同一故事程序设计中,函数A自己调用自己,称为直接递归调用。镜子A和镜子B相对放在一起,你会发现什么现象呢?对了,我们会发现镜子A中有镜子B的映象,镜子B中又镜子A的映象,这样层层叠叠,无穷无尽。AB在程序设计中,像这种函数A调用函数B,函数B再反过来调用函数A的算法,称为间接递归调用。间接递归调用
递归算法是语言设计中的一种重要方法,只需少量的程序就可描述出解题过程,但是递归执行的过程比较复杂。
递归算法关键:
1.递归关系 2.递归终止条件
递归实例1设计一个vb程序,
输入正整数n,求出n的阶乘
5!=5*4*3*2*1=5*4!
4!=4*3*2*1=4*3!
3!=3*2*1=3*2!
2!=2*1=2*1!
1!=1
1:对于任意一个整数n (n>1):
n!=n*(n-1)!
2:终止条件 n=1
1!=1‘1、终止条件:n=1 时jc(1)=1
‘2、对于任意n>1找出jc(n)和jc(n-1)之间的关系n!=n*(n-1)!Function jc(n as integer) as integer
If n =1 then
jc(1)=1
else
jc(n) =n*jc(n-1)
End if
End functionjc=1jc= n*jc(n-1)递归函数的调用Function jc(byval n as integer) as integer
If n =1 then
jc=1
else
jc=n*jc(n-1)
End if
End Function
Private Sub Command1_Click()
a = Val(Text1.Text)
b = jc(a)
Label1.Caption = str(a)+“的阶乘为:”Str(b)
End Subjc(3)
=3*jc(2)jc(2)
=2*jc(1)jc(1)=1=2*1
=2=3*2
=6返回返回jc(3)
=3*jc(2)返回返回jc(3)
=3*jc(2)返回返回当n=3时y=jc(3)递归算法的基本思想是把规模较大的、较难解决的问题变成规模较小的、容易解决的同一问题,规模较小的问题又变成规模更小的问题,当问题小到一定程度时,可以直接得出它的解,从而得到原来问题的解。
即采用“大事化小、小事化了”的基本思想。jc=3*jc(2)jc=2*jc(1)jc=1递归实例2有5个人坐在一起,问第5个人多少岁,他说比第4个人大2岁;问第4个人岁数,他说比第3个人大2岁;问第3个人,又说比第2个大2岁;问第2个人,说比第1个人大2岁;最后问第1个人,他说他10岁;请问第5个人多大?
终止条件:第一个人10岁
递归关系:每一个人的年龄都比其前1个人的年龄大
age(5)=age(4)+2
age(4)=age(3)+2
age(3)=age (2)+2
age(2)=age(1)+2
age(1)=10
Function age (n as Integer)as Integer
If then
age =________
Else
age=___________
End if
End Functionn=110age(n-1)+2习题1:斐波那契数列问题斐波那契数列,又称黄金分割数列,指的是这样一个数列:
1、1、2、3、5、8、13、21、34、55……
这个数列从第3项开始,每一项都等于前两项之和。
设计一个VB程序
求:数列中的第n项是多少?
1、终止条件:最初两项值为1
2、递归关系:第n项的值是它之前两项之和 ( n大于3 )
求第N个斐波纳切数
if 前两项 then
斐波纳切数=1
else
斐波纳切数=前两个斐波纳切数之和
end ifFunction Fib (n as Integer)as Integer
If then
Fib =__
Else
Fib =__________________
End if
End Functionn<31Fib (n-2)+Fib (n-1)习题2:小猴吃桃问题有一天小猴子摘若干个桃子,当即吃了一半还觉得不过瘾,又多吃了一个。第二天接着吃剩下桃子中的一半,仍觉得不过瘾又多吃了一个,以后小猴子都是吃尚存桃子一半多一个。到第10天早上小猴子再去吃桃子的时候,看到只剩下一个桃子。问小猴子第一天共摘下了多少个桃子?
递归算法描述:
??? Function 你有多少桃子?(第几天)
?? If Then
? Else
End if
??? End Function桃子数=第n天的桃子数第n+1天的桃子数 2-1=第n天的桃子数=(第n+1天的桃子数+1)*2( 明天的桃子数+1)*2第10天 桃子数=1算法实现:
Function Tao(days As Integer) As Integer
If days = 10 Then
Tao = 1
Else
Tao = (Tao(days + 1) + 1) * 2
End If
End FunctionTao(1)=(Tao(2)+1)*2Tao(2)=(Tao(3)+1)*2Tao(3)=(Tao(4)+1)*2 Tao(8)=(Tao(9)+1)*2Tao(9)=(Tao(10)+1)*2Tao(10)= 1调用调用调用调用调用返回返回返回返回返回习题3:求最大公约数早在公元前300年左右,欧几里得就在他的著作《几何原本》中给出了高效的解法——辗转相除法。
辗转相除法的方法是用较大的数X除以较小的数Y,得到余数Z
如果余数为0,则较小数Y就是两者的最大公约数。
例如:27和9的最大公约数就是9
如果余数不为0,则较小数Y与余数Z的最大公约数就是X与Y的的
最大公约数
例如:140和63 的最大公约数就是63与14的最大公约数,
63与14的最大公约数就是14和7
14和7的最大公约数7
Function GYS(x as Integer,y as Integer)as Integer
Dim z as Integer
z=
If then
GYS=
Else
GYS=
End if
End Function求X与Y的公约数:
Z是X除Y得到的余数
If then
公约数=
Else
公约数=
End if YY 和 Z的公约数Z为0 X mod YZ=0YGYS( Y , Z )3、课堂小结递归算法实现的要点递归调用必须是有限制的,有限才有意义。构成递归的必须满足以下条件:
(1)有明确的结束递归的边界条件(又称终止条件)以及结束时的边界值;通过条件语句(If语句)来实现
(2)函数的描述中包含其本身,即能用递归形式表示Function jc(n as integer) as integer
If n =1 then
jc=1
else
jc=n*jc(n-1)
End if
End fun_ction
同课章节目录
- 第一章 算法和算法的表示
- 1.1 使用计算机解决问题的一般过程
- 1.2 确定解决问题的方法
- 1.3 把解决问题的方法步骤化
- 1.4 算法的概念和表示方法
- 第二章 算法实例
- 2.1 枚举算法
- 2.2 解析算法
- 2.3 排序
- 2.4 查找
- 第三章 面向对象程序设计的基本知识
- 3.1 面向对象程序设计方法简介
- 3.2 在可视化的程序设计环境VB中建立一个应用程序
- 第四章 VB程序设计初步
- 4.1 基本数据类型、常量、变量
- 4.2 基本运算和表达式
- 4.3 语句
- 4.4 过程和函数
- 第五章 算法实例的程序实现
- 5.1 枚举算法的程序实现
- 5.2 解析算法的程序实现
- 5.3 排序算法的程序实现
- 5.4 查找算法的程序实现
- 5.5 递归算法实例及程序实现
- 非试题类资料
