北师大版七年级数学下册1.5平方差公式课件(18张)
文档属性
| 名称 | 北师大版七年级数学下册1.5平方差公式课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 16:18:08 | ||
图片预览


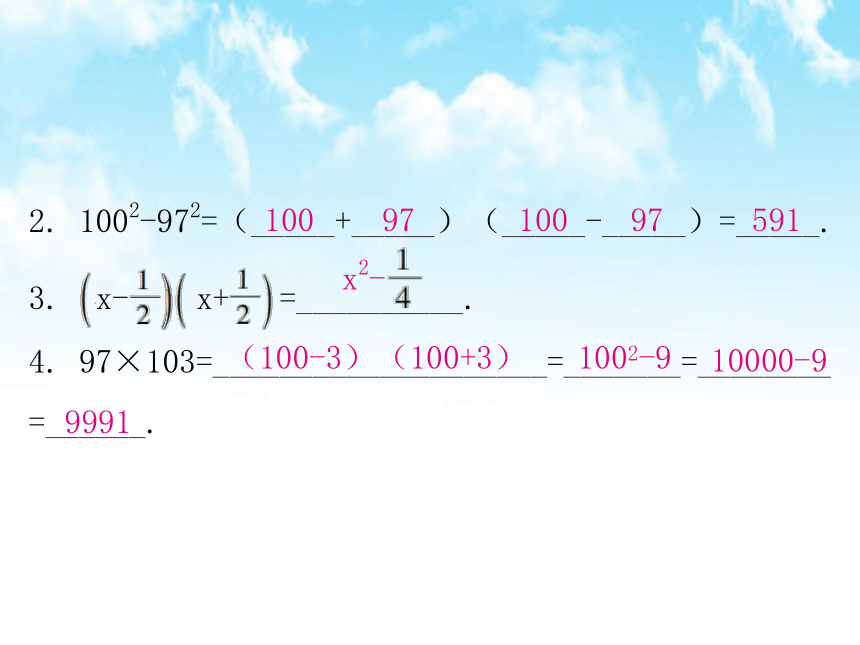



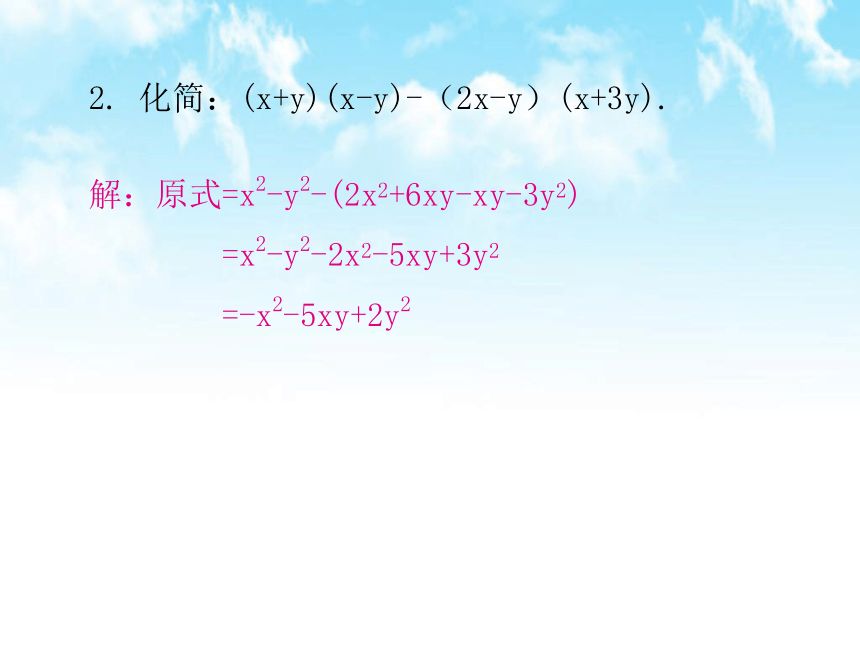
文档简介
(共18张PPT)
5
平方差公式
第一章
整式的乘除
1.
填空:
(1)(x+1)(x-1)=__________;
(2)(m+2)(m-2)=__________;
(3)(2x+1)(2x-1)=__________;
(4)(3x+2)(3x-2)=__________.
课前预习
x2-1
m2-4
4x2-1
9x2-4
2.
1002-972=(_____+_____)(_____-_____)=_____.
3.
x-
x+
=__________.
4.
97×103=____________________=_______=________
=______.
100
97
591
100
97
x2-
(100-3)(100+3)
1002-9
10000-9
9991
课堂讲练
新知1
平方差公式
典型例题
【例1】计算:
(1)(2x+3y)(3y-2x);
(2)(-x+y)(-x-y)(y2+x2).
解:(1)原式=9y2-4x2.
(2)原式=(x2-y2)(y2+x2)
=x4-y4.
【例2】计算:3(2a+1)(2a-1)-4a(a-2).
解:原式=3(4a2-1)-4a2+8a
=12a2-3-4a2+8a
=8a2+8a-3.
解:原式=5x2-5y2.
模拟演练
1.
计算:
(1)(-2xy+3y)(-2xy-3y);
(2)(2x-y)(y+2x)-(2y+x)(2y-x);
(3)
-2x2+
-2x2-
.
解:原式=4x2y2-9y2.
解:原式=4x4-
.
2.
化简:(x+y)(x-y)-(2x-y)(x+3y).
解:原式=x2-y2-(2x2+6xy-xy-3y2)
=x2-y2-2x2-5xy+3y2
=-x2-5xy+2y2
新知2
利用平方差公式进行简化运算
典型例题
【例3】利用平方差公式计算:
(1)2
002×1
998;(2)2
0092-2
008×2
010.
解:(1)(2
000+2)(2
000-2)
=2
0002-4=4
000
000-4=3
999
996.
(2)2
0092-2
008×2
010
=2
0092-(2
009-1)(2
009+1)
=2
0092-2
0092+1=1.
【例4】简便计算:2
008×2
010-2
0092=__________;
22
007·
=__________.
-1
模拟演练
3.
利用平方差公式计算:
(1)1
999×2
001;
(2)992-1.
4.
计算:2
0042-2
003×2
005=__________.
解:1
999×2
001=(2
000-1)×(2
000+1)
=2
0002-1=4
000
000-1=3
999
999.
解:992-1=(99+1)×(99-1)
=100×98
=9800.
1
课后作业
夯实基础
新知1
平方差公式
1.
若a2-b2=-
,a+b=-
,则a-b的值为
(
)
A.
B.
-
C.
2
D.
4
2.
用平方差公式计算(x-1)(x+1)(x2+1)结果正确的是
(
)
A.
x4-1
B.
x4+1
C.(x-1)4
D.(x+1)4
A
A
3.
下列各式中,能用平方差公式计算的是
(
)
A.
a-
b
a-
b
B.
a-
b
-a+
b
C.
-a-
b
a-
b
D.
-a-
b
a+
b
4.
下列各式计算正确的是
(
)
A.
2a2+3a2=5a4
B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2
D.
a3·(-2a)=-2a3
C
C
5.
已知a+b=53,a-b=38,则a2-b2的值为
(
)
A.15
B.
38
C.53
D.
2
014
6.(a+3b)(a-3b)计算的结果是
(
)
A.
a2-6b2
B.
a2-9b2
C.
a2-6ab+9b2
D.
a2+6ab+9b2
7.
如果(2a+2b-3)(2a+2b+3)=40,那么a+b=_____.
D
B
新知2
利用平方差公式进行简化运算
8.
计算:2
017×1
983=______________.
9.
化简:6×(7+1)(72+1)(74+1)(78+1)(716+1)+1=__________.
10.
计算:1232-122×124.
3
999
711
732
解:原式=1232-(123-1)(123+1)
=1232-(1232-12)
=1.
能力提升
11.
请先观察下列算式,再填空:
32-12=8×1,52-32=8×2.
①72-52=8×__________;
②92-(__________)2=8×4;
③(__________)2-92=8×5;
④132-(__________)2=8×__________;
….
3
7
11
11
6
(1)通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来.
(2)你能运用本章所学的平方差公式来说明你的猜想的正确性吗?
解:(1)(n+2)2-n2=8×
(n≥1).
(n+2)+n
4
(2)(n+2)2-n2=(n+2+n)(n+2-n)=(2n+2)×2=8×
(n+2+n)=8×
.
(n+2)+n
4
12.
阅读下文,寻找规律:
已知x≠1,计算:(1+x)(1-x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,
….
(1)观察上式,猜想:
(1-x)(1+x+x2+…+xn)=__________.
(2)根据你的猜想,计算:
①(1-2)(1+2+22+…+22
014);
②2+22+23+…+2n.
1-xn+1
解:①(1-2)(1+2+22+…+22
014)=1-22
015.
②2+22+23+24+…+2n=(1-2n+1)÷(1-2)-1=2n+1-2.
5
平方差公式
第一章
整式的乘除
1.
填空:
(1)(x+1)(x-1)=__________;
(2)(m+2)(m-2)=__________;
(3)(2x+1)(2x-1)=__________;
(4)(3x+2)(3x-2)=__________.
课前预习
x2-1
m2-4
4x2-1
9x2-4
2.
1002-972=(_____+_____)(_____-_____)=_____.
3.
x-
x+
=__________.
4.
97×103=____________________=_______=________
=______.
100
97
591
100
97
x2-
(100-3)(100+3)
1002-9
10000-9
9991
课堂讲练
新知1
平方差公式
典型例题
【例1】计算:
(1)(2x+3y)(3y-2x);
(2)(-x+y)(-x-y)(y2+x2).
解:(1)原式=9y2-4x2.
(2)原式=(x2-y2)(y2+x2)
=x4-y4.
【例2】计算:3(2a+1)(2a-1)-4a(a-2).
解:原式=3(4a2-1)-4a2+8a
=12a2-3-4a2+8a
=8a2+8a-3.
解:原式=5x2-5y2.
模拟演练
1.
计算:
(1)(-2xy+3y)(-2xy-3y);
(2)(2x-y)(y+2x)-(2y+x)(2y-x);
(3)
-2x2+
-2x2-
.
解:原式=4x2y2-9y2.
解:原式=4x4-
.
2.
化简:(x+y)(x-y)-(2x-y)(x+3y).
解:原式=x2-y2-(2x2+6xy-xy-3y2)
=x2-y2-2x2-5xy+3y2
=-x2-5xy+2y2
新知2
利用平方差公式进行简化运算
典型例题
【例3】利用平方差公式计算:
(1)2
002×1
998;(2)2
0092-2
008×2
010.
解:(1)(2
000+2)(2
000-2)
=2
0002-4=4
000
000-4=3
999
996.
(2)2
0092-2
008×2
010
=2
0092-(2
009-1)(2
009+1)
=2
0092-2
0092+1=1.
【例4】简便计算:2
008×2
010-2
0092=__________;
22
007·
=__________.
-1
模拟演练
3.
利用平方差公式计算:
(1)1
999×2
001;
(2)992-1.
4.
计算:2
0042-2
003×2
005=__________.
解:1
999×2
001=(2
000-1)×(2
000+1)
=2
0002-1=4
000
000-1=3
999
999.
解:992-1=(99+1)×(99-1)
=100×98
=9800.
1
课后作业
夯实基础
新知1
平方差公式
1.
若a2-b2=-
,a+b=-
,则a-b的值为
(
)
A.
B.
-
C.
2
D.
4
2.
用平方差公式计算(x-1)(x+1)(x2+1)结果正确的是
(
)
A.
x4-1
B.
x4+1
C.(x-1)4
D.(x+1)4
A
A
3.
下列各式中,能用平方差公式计算的是
(
)
A.
a-
b
a-
b
B.
a-
b
-a+
b
C.
-a-
b
a-
b
D.
-a-
b
a+
b
4.
下列各式计算正确的是
(
)
A.
2a2+3a2=5a4
B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2
D.
a3·(-2a)=-2a3
C
C
5.
已知a+b=53,a-b=38,则a2-b2的值为
(
)
A.15
B.
38
C.53
D.
2
014
6.(a+3b)(a-3b)计算的结果是
(
)
A.
a2-6b2
B.
a2-9b2
C.
a2-6ab+9b2
D.
a2+6ab+9b2
7.
如果(2a+2b-3)(2a+2b+3)=40,那么a+b=_____.
D
B
新知2
利用平方差公式进行简化运算
8.
计算:2
017×1
983=______________.
9.
化简:6×(7+1)(72+1)(74+1)(78+1)(716+1)+1=__________.
10.
计算:1232-122×124.
3
999
711
732
解:原式=1232-(123-1)(123+1)
=1232-(1232-12)
=1.
能力提升
11.
请先观察下列算式,再填空:
32-12=8×1,52-32=8×2.
①72-52=8×__________;
②92-(__________)2=8×4;
③(__________)2-92=8×5;
④132-(__________)2=8×__________;
….
3
7
11
11
6
(1)通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来.
(2)你能运用本章所学的平方差公式来说明你的猜想的正确性吗?
解:(1)(n+2)2-n2=8×
(n≥1).
(n+2)+n
4
(2)(n+2)2-n2=(n+2+n)(n+2-n)=(2n+2)×2=8×
(n+2+n)=8×
.
(n+2)+n
4
12.
阅读下文,寻找规律:
已知x≠1,计算:(1+x)(1-x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,
….
(1)观察上式,猜想:
(1-x)(1+x+x2+…+xn)=__________.
(2)根据你的猜想,计算:
①(1-2)(1+2+22+…+22
014);
②2+22+23+…+2n.
1-xn+1
解:①(1-2)(1+2+22+…+22
014)=1-22
015.
②2+22+23+24+…+2n=(1-2n+1)÷(1-2)-1=2n+1-2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
