北师大版七年级数学下册1.3同底数幂的除法课件(25张)
文档属性
| 名称 | 北师大版七年级数学下册1.3同底数幂的除法课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 343.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 16:16:48 | ||
图片预览





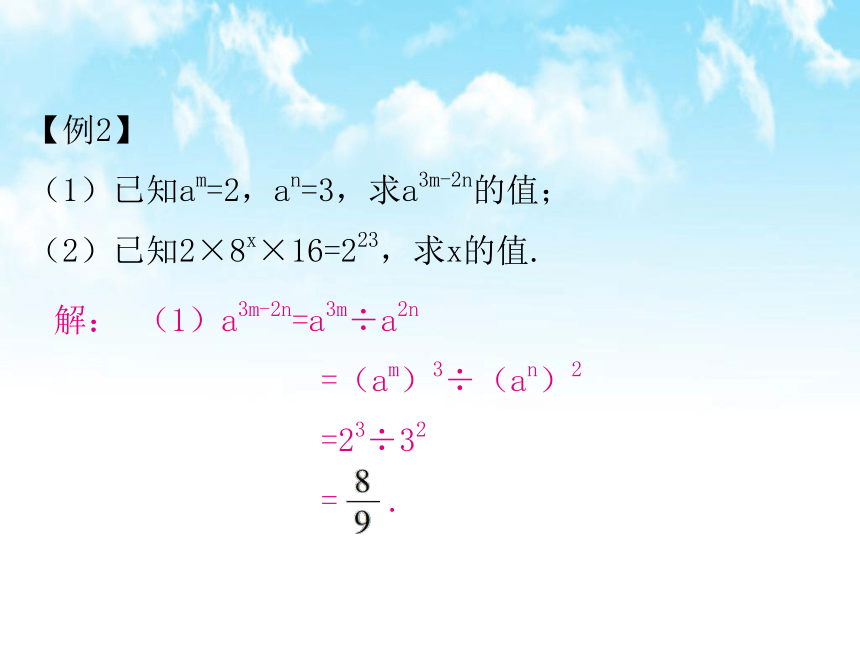



文档简介
(共25张PPT)
3
同底数幂的除法
第一章
整式的乘除
1.
如果(x-2)0有意义,那么x的取值范围是
(
)
A.
x>2
B.
x<2
C.
x=2
D.
x≠2
2.
用分数表示(-2)-2,正确的是
(
)
A.
B.
-
C.
D.
-
课前预习
D
C
3.
同底数幂的除法法则是:同底数幂相除,底数不变,指数__________.
用字母表示为
__________________
_______________________________.
4.
若3x=10,3y=5,则32x-y=__________.
5.
某种电子元件的面积大约为0.000
000
69
mm2,将0.000
000
69这个数用科学记数法表示为__________.
相减
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
20
6.9×10-7
课堂讲练
新知1
同底数幂的除法
典型例题
【例1】计算:
(1)(-x)10÷(-x)3;
(2)(-x2y)4÷(-x2y)3;
(3)(x-2)9÷(2-x)4;
(4)(xy)10÷(-xy)2÷(xy)3.
解:(1)
原式=(-x)10-3=(-x)7=-x7.
(2)
原式=(-x2y)4-3=(-x2y)1=-x2y.
(3)
原式=(x-2)9÷(x-2)4
=(x-2)9-4
=(x-2)5.
(4)
原式=(xy)10÷(xy)2÷(xy)3
=(xy)10-2-3
=(xy)5
=x5y5.
【例2】
(1)已知am=2,an=3,求a3m-2n的值;
(2)已知2×8x×16=223,求x的值.
解:
(1)a3m-2n=a3m÷a2n
=(am)3÷(an)2
=23÷32
=
.
(2)因为2×8x×16=223,
所以2×(23)x×24=223.
所以2×23x×24=223.
所以1+3x+4=23.
解得x=6.
模拟演练
1.
计算:
(1)
a7÷a4;
(2)(-x)6÷(-x)3.
解:(1)a7÷a4=a7-4=a3.
(2)(-x)6÷(-x)3=(-x)6-3=(-x)3=-x3.
2.
已知:5a=4,5b=6,5c=9.
(1)求52a+c-b的值;
(2)试说明:2b=a+c.
解:(1)52a+c-b=52a×5c÷5b
=(5a)2×5c÷5b
=42×9÷6=24.
(2)因为5a+c=5a×5c=4×9=36,
52b=(5b)2=62=36,
所以5a+c=52b.
所以a+c=2b.
新知2
零指数幂和负整数指数幂的意义
典型例题
【例3】计算:
(1)
810÷810;(2)
10-2;(3)
×10-1.
解:(1)810÷810=810-10=80=1.
(2)
10-2=
=
.
(3)
×10-1=1×
=
.
【例4】计算:2-2×43+
-(-2)4.
解:原式=
×64+1-16
=16+1-16
=1.
模拟演练
3.
计算:-23-
+(π-1)0.
解:原式=-8-4+1
=-11.
4.
计算:(2-π)0-
+(-1)2
018.
解:原式=1-2+1
=0.
新知3
用科学记数法表示绝对值较小的数
典型例题
【例5】(1)科学家发现一种病毒的直径为0.000
043
mm,用科学记数法表示这个数为__________.
(2)若0.000
028
3=2.83×10x,则x=__________.
4.3×10-5
-5
【例6】如果规定:0.1=
=10-1,0.01=
=10-2,0.001=
=10-3,….
(1)你能用幂的形式表示0.000
1,0.000
01吗?
(2)你能将0.000
001
768表示成a×10n的形式吗?(其中1≤a<10,n是负整数)
解:(1)0.000
1=10-4,0.000
01=10-5.
(2)0.000
001
768=1.768×10-6.
【例7】用科学记数法表示下列各数:
0.000
1,0.000
13,0.000
000
204,-0.000
000
004
06.
解:0.000
1=1×10-4;
0.000
13=1.3×10-4;
0.000
000
204=2.04×10-7;
-0.000
000
004
06=-4.06×10-9.
模拟演练
5.
(1)用科学记数法表示下列各数:
32
200
000=_________________;
0.000
020
04=_________________.
(2)还原用科学记数法表示的数:
-3.014×10-4=___________________,
8.21×106=____________________.
3.22×107
2.004×10-5
-0.000
301
4
8
210
000
6.
用10的整数指数幂表示下列各数:
100
000,0.1,1,0.000
01,-0.001.
解:100
000=105;
0.1=10-1;
1=100;
0.000
01=10-5;
-0.001=-10-3.
7.
一块900
mm2的芯片上能集成10亿个元体,每一个这样的元体约占多少平方毫米?合多少平方米?(用科学记数法表示)
解:900÷1
000
000
000=9×10-7(mm2),
9×10-7÷1
000
000=9×10-13(m2).
答:每个这样的元件约占9×10-7mm2,合9×10-13
m2.
课后作业
夯实基础
新知1
同底数幂的除法
1.
下列计算正确的是
(
)
A.
a3×a2=a6
B.
a3÷a=a3
C.
a2+a2=a4
D.(a2)2=a4
2.
下列计算正确的是
(
)
A.
2a+b=2ab
B.
(-a)2=a2
C.
a6÷a2=a3
D.
a3·a2=a6
D
B
3.
下列计算正确的是
(
)
A.
a3+a2=a5
B.
a3·a2=a5
C.(a3)2=a5
D.
a8÷a2=a4
4.
下列运算正确的是
(
)
A.
m·m=2m
B.(mn)3=mn3
C.(m2)3=m6
D.
m6÷m3=m2
5.
计算a8÷a4结果正确的是
(
)
A.
a
B.
a2
C.
a3
D.
a4
6.
若5x=2,5y=3,则53x-2y的值为__________.
B
C
D
新知2
零指数幂和负整数指数幂的意义
7.(-3)2-(π-3.14)0=__________.
8.
|-2|-(π-3)0=__________.
9.(-2)2+(π-3)0+
-1=__________.
8
1
2
新知3
用科学记数法表示绝对值较小的数
10.
肥皂泡沫的泡壁厚度大约是0.000
7
mm,则数据0.000
7用科学记数法表示为__________.
11.
细胞的直径只有1微米,即0.000
001
m,用科学记数法表示0.000
001为__________.
7×10-4
1×10-6
能力提升
12.
计算:
(1)a2·a4+(a3)2;
(2)(-a2)2·a5+a10÷a-(-2a3)3;
(3)先化简,再求值:x2-2(xy-y2)+3
xy
-y2
,其中x=-2,y=2.
解:(1)a2·a4+(a3)2=a6+a6=2a6.
(2)(-a2)2·a5+a10÷a-(-2a3)3=a9+a9+8a9=10a9.
(3)x2-2(xy-y2)+3
xy-y2
=x2-2xy+2y2+2xy-3y2=x2-y2,
当x=-2,y=2时,原式=0.
13.
已知(ax)y=a6,(ax)2÷ay=a3.
(1)求xy和2x-y的值;
(2)求2x2y-xy2的值.
解:(1)因为(ax)y=a6,(ax)2÷ay=a3,
所以axy=a6,a2x÷ay=a2x-y=a3.
所以xy=6,2x-y=3.
(2)2x2y-xy2=xy(2x-y)=6×3=18.
3
同底数幂的除法
第一章
整式的乘除
1.
如果(x-2)0有意义,那么x的取值范围是
(
)
A.
x>2
B.
x<2
C.
x=2
D.
x≠2
2.
用分数表示(-2)-2,正确的是
(
)
A.
B.
-
C.
D.
-
课前预习
D
C
3.
同底数幂的除法法则是:同底数幂相除,底数不变,指数__________.
用字母表示为
__________________
_______________________________.
4.
若3x=10,3y=5,则32x-y=__________.
5.
某种电子元件的面积大约为0.000
000
69
mm2,将0.000
000
69这个数用科学记数法表示为__________.
相减
am÷an=am-n
(a≠0,m,n都是正整数,且m>n)
20
6.9×10-7
课堂讲练
新知1
同底数幂的除法
典型例题
【例1】计算:
(1)(-x)10÷(-x)3;
(2)(-x2y)4÷(-x2y)3;
(3)(x-2)9÷(2-x)4;
(4)(xy)10÷(-xy)2÷(xy)3.
解:(1)
原式=(-x)10-3=(-x)7=-x7.
(2)
原式=(-x2y)4-3=(-x2y)1=-x2y.
(3)
原式=(x-2)9÷(x-2)4
=(x-2)9-4
=(x-2)5.
(4)
原式=(xy)10÷(xy)2÷(xy)3
=(xy)10-2-3
=(xy)5
=x5y5.
【例2】
(1)已知am=2,an=3,求a3m-2n的值;
(2)已知2×8x×16=223,求x的值.
解:
(1)a3m-2n=a3m÷a2n
=(am)3÷(an)2
=23÷32
=
.
(2)因为2×8x×16=223,
所以2×(23)x×24=223.
所以2×23x×24=223.
所以1+3x+4=23.
解得x=6.
模拟演练
1.
计算:
(1)
a7÷a4;
(2)(-x)6÷(-x)3.
解:(1)a7÷a4=a7-4=a3.
(2)(-x)6÷(-x)3=(-x)6-3=(-x)3=-x3.
2.
已知:5a=4,5b=6,5c=9.
(1)求52a+c-b的值;
(2)试说明:2b=a+c.
解:(1)52a+c-b=52a×5c÷5b
=(5a)2×5c÷5b
=42×9÷6=24.
(2)因为5a+c=5a×5c=4×9=36,
52b=(5b)2=62=36,
所以5a+c=52b.
所以a+c=2b.
新知2
零指数幂和负整数指数幂的意义
典型例题
【例3】计算:
(1)
810÷810;(2)
10-2;(3)
×10-1.
解:(1)810÷810=810-10=80=1.
(2)
10-2=
=
.
(3)
×10-1=1×
=
.
【例4】计算:2-2×43+
-(-2)4.
解:原式=
×64+1-16
=16+1-16
=1.
模拟演练
3.
计算:-23-
+(π-1)0.
解:原式=-8-4+1
=-11.
4.
计算:(2-π)0-
+(-1)2
018.
解:原式=1-2+1
=0.
新知3
用科学记数法表示绝对值较小的数
典型例题
【例5】(1)科学家发现一种病毒的直径为0.000
043
mm,用科学记数法表示这个数为__________.
(2)若0.000
028
3=2.83×10x,则x=__________.
4.3×10-5
-5
【例6】如果规定:0.1=
=10-1,0.01=
=10-2,0.001=
=10-3,….
(1)你能用幂的形式表示0.000
1,0.000
01吗?
(2)你能将0.000
001
768表示成a×10n的形式吗?(其中1≤a<10,n是负整数)
解:(1)0.000
1=10-4,0.000
01=10-5.
(2)0.000
001
768=1.768×10-6.
【例7】用科学记数法表示下列各数:
0.000
1,0.000
13,0.000
000
204,-0.000
000
004
06.
解:0.000
1=1×10-4;
0.000
13=1.3×10-4;
0.000
000
204=2.04×10-7;
-0.000
000
004
06=-4.06×10-9.
模拟演练
5.
(1)用科学记数法表示下列各数:
32
200
000=_________________;
0.000
020
04=_________________.
(2)还原用科学记数法表示的数:
-3.014×10-4=___________________,
8.21×106=____________________.
3.22×107
2.004×10-5
-0.000
301
4
8
210
000
6.
用10的整数指数幂表示下列各数:
100
000,0.1,1,0.000
01,-0.001.
解:100
000=105;
0.1=10-1;
1=100;
0.000
01=10-5;
-0.001=-10-3.
7.
一块900
mm2的芯片上能集成10亿个元体,每一个这样的元体约占多少平方毫米?合多少平方米?(用科学记数法表示)
解:900÷1
000
000
000=9×10-7(mm2),
9×10-7÷1
000
000=9×10-13(m2).
答:每个这样的元件约占9×10-7mm2,合9×10-13
m2.
课后作业
夯实基础
新知1
同底数幂的除法
1.
下列计算正确的是
(
)
A.
a3×a2=a6
B.
a3÷a=a3
C.
a2+a2=a4
D.(a2)2=a4
2.
下列计算正确的是
(
)
A.
2a+b=2ab
B.
(-a)2=a2
C.
a6÷a2=a3
D.
a3·a2=a6
D
B
3.
下列计算正确的是
(
)
A.
a3+a2=a5
B.
a3·a2=a5
C.(a3)2=a5
D.
a8÷a2=a4
4.
下列运算正确的是
(
)
A.
m·m=2m
B.(mn)3=mn3
C.(m2)3=m6
D.
m6÷m3=m2
5.
计算a8÷a4结果正确的是
(
)
A.
a
B.
a2
C.
a3
D.
a4
6.
若5x=2,5y=3,则53x-2y的值为__________.
B
C
D
新知2
零指数幂和负整数指数幂的意义
7.(-3)2-(π-3.14)0=__________.
8.
|-2|-(π-3)0=__________.
9.(-2)2+(π-3)0+
-1=__________.
8
1
2
新知3
用科学记数法表示绝对值较小的数
10.
肥皂泡沫的泡壁厚度大约是0.000
7
mm,则数据0.000
7用科学记数法表示为__________.
11.
细胞的直径只有1微米,即0.000
001
m,用科学记数法表示0.000
001为__________.
7×10-4
1×10-6
能力提升
12.
计算:
(1)a2·a4+(a3)2;
(2)(-a2)2·a5+a10÷a-(-2a3)3;
(3)先化简,再求值:x2-2(xy-y2)+3
xy
-y2
,其中x=-2,y=2.
解:(1)a2·a4+(a3)2=a6+a6=2a6.
(2)(-a2)2·a5+a10÷a-(-2a3)3=a9+a9+8a9=10a9.
(3)x2-2(xy-y2)+3
xy-y2
=x2-2xy+2y2+2xy-3y2=x2-y2,
当x=-2,y=2时,原式=0.
13.
已知(ax)y=a6,(ax)2÷ay=a3.
(1)求xy和2x-y的值;
(2)求2x2y-xy2的值.
解:(1)因为(ax)y=a6,(ax)2÷ay=a3,
所以axy=a6,a2x÷ay=a2x-y=a3.
所以xy=6,2x-y=3.
(2)2x2y-xy2=xy(2x-y)=6×3=18.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
