人教版七年级下册数学8.3实际问题与二元一次方程组课件 (共33张PPT)
文档属性
| 名称 | 人教版七年级下册数学8.3实际问题与二元一次方程组课件 (共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-13 08:25:04 | ||
图片预览











文档简介
课件33张PPT。8.3实际问题与二元一次方程组
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解:设悟空行走速度是每分钟x里, 风速是每分钟y里,4(x-y)=600 x=200 y=50答:风速是每分钟50里.4(x+y)=1000 解得:依题意得
列方程组解应用题的步骤: 审题
设未知数
列方程组
解方程组
检验
答养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?自主探究1、怎样检验他的估计呢?2、题目中包含怎样的等量关系?这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
你的答案对了吗?解得:205化简得:①②解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg.依题意得
练一练: 长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?解:设应取2米的x段,1米的y段,努力提高自我答:小明估计不准确.2米的应取8段,1米的 应取2段.解得:依题意得努力提高自我 试一试 :某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,x+2y=16802x+y=2280解得:x=960y=360(2)若7个餐厅同时开放,则有
5×960+2×360=5320答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.5320>5300依题意得
想一想 :某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?解:设该公司应安排x天精加工,y天粗加工, x+y=15
6x+16y=140解 得:x=10
y=5答:该公司应安排x10天精加工,5天粗加工.拓展延伸依题意得
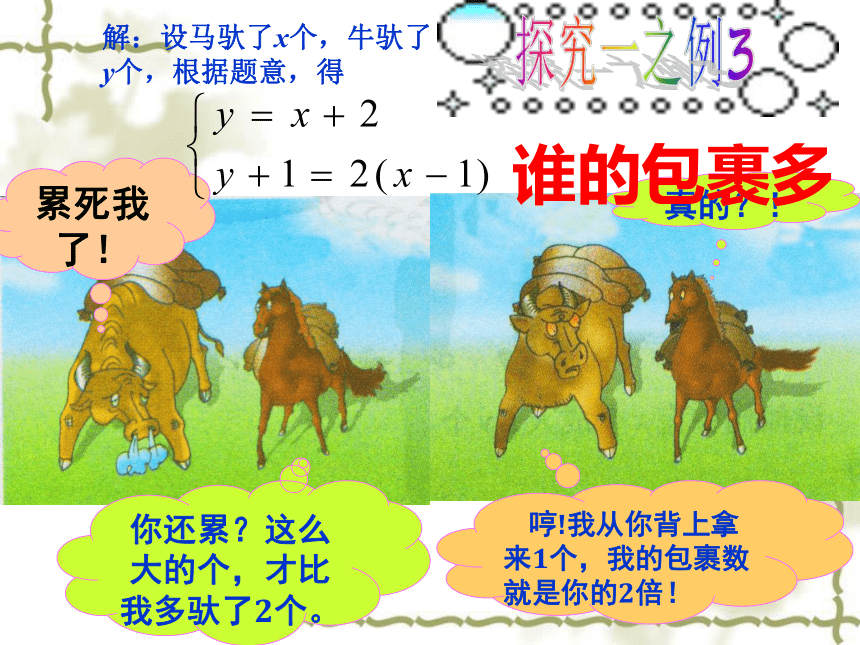
哼!我从你背上拿来1个,我的包裹数就是你的2倍!累死我了!你还累?这么大的个,才比我多驮了2个。真的?!谁的包裹多解:设马驮了x个,牛驮了y个,根据题意,得探究一之例3 现有20人生产某种零件,每人每天可以生产螺杆2个或者做螺帽3个, 如果1个螺杆和2个螺帽可以做成一个零件, 那么能否把这 20人分成两部分, 一部分人做螺杆, 一部分人做螺帽,使每天做成的螺杆和螺帽正好配套 ?分析:设x人生产螺杆,则可以生产2x个;
y人生产螺帽,则可以生产3y个。根据题意,得注意:此方程没有整数解如果是28人呢?探究一之例4做一做:1、把长方形纸片折成面积相等的两个小长方形,有哪些折法?2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?●●●● 按面积分割长方形的问题可转化为分割边长的问题。归纳例1:据以往的统计资料,甲、乙两种作物的单位面积产量的比是 1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是 3 : 4 (结果取整数)? 应用数学、解决实际问题甲种作物的总产量 = 甲的单位面积产量×甲的种植面积乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积解:设AE为 x 米,BE为 y 米,由题意得:ABCD●E┓
xy答: 过长方形土地的长边上离一端约106米处,
把这块地分为两个长方形.较大一块地种甲种作
物,较小一块地种乙种作物.ABCD●E┓
yx解:设CE为 x 米,BE为 y 米,由题意得:答: 过长方形土地的短边上离一端约53米处,
把这块地分为两个长方形.较大一块地种甲
种作物,较小一块地种乙种作物. 据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,从长方形边的中点出发引出一条线段怎样把这
块地分为两部分,使甲、乙两种作物的总产量的比是 3 : 4
(结果取整数)? 变式: 例2: 小龙在拼图时,发现8个一样大的小长
方形,恰好可以拼成一个大长方形,如图甲所示,
陈晔看见了说“我来试一试”,结果陈晔七拼八凑,
拼成一个如图乙的正方形,中间留下一个洞,恰
好是边长2mm的小正方形,你能算出小长方形
的长和宽吗?甲乙 例3: 一个长方形,它的长减少4cm,
宽增加2cm,所得的是一个正方形,它的
面积与长方形的面积相等,求原长方形的
长与宽。解:设长方形的长为xcm,宽为ycm,
由题意得:
课前准备:某班文艺小组购买每张3元、5元的杂技票
共计20张,用去76元,问其中3元票、5元
票各几张? 解方程组得: 答:3元票12张,5元票8张。 1、列方程组解应用题的步骤是什么?审:审题,分析题中已知什么,求什么,明确各数量之间的关系 设:设未知数(一般求什么,就设什么为x、y,注意单位) 找:找出能够表示应用题全部意义的两个相等关系 列:根据这两个相等关系列出需要的代数式,进而列出两个方程,
组成方程 解:解所列方程组,得未知数的值 验:检验求得的值是否正确和符合实际情形 答:写出答案(包括单位名称) 2、列方程组解应用题的关键是什么?或者说让大家感觉最难的,最困惑的部分是什么?找到题中的等量关系 如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?审题 2.已知的量:3.要求的量:1.运费的单位“元∕(吨·千米)”的含义 原料从A地运回工厂,每吨运费159元 产品从工厂运到B地,每吨运费162元 铁路、公路运费的单价已知量与未知量的关系原料的铁路运费+原料的公路运费=每吨原料的运费产品的铁路运费+产品的公路运费=每吨产品的运费答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米) 解方程组得:整理方程组得: 探索分析,解决问题例题:(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?设问1.原料的数量与产品的数量一样多吗?(不一样)设问2.那些量设为未知数? 销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .设问3.如何分析题目中的数量关系?能否用列表分析?列表分析:1.5(20X)1.2(110X)1.5(10Y)1.2(120Y)1.5(20X+10Y)1.2(110X+120Y)8000X1000Y由上表可列方程组 解这个方程组,得 :销售款为: 原料费为: 运输费为: 8000X300=2400000(元) 1000X400=400000(元) 15000+97200=112200(元) 所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)答:销售款比原料费与运输费的和多1887800元。 1. 电力行业中峰谷的含义是用山峰和山谷来形象地比喻用电负荷特性的变化幅度一般白天的用电比较集中、用电功率比较大,而夜里人们休息时用电比较小,所以通常白天的用电称为是高峰用电,即8:00~22:00,深夜的用电是低谷用电即22:00~次日8:00.若某地的高峰电价为每千瓦时0.56元;低谷电价为每千瓦时0.28元.八月份小彬家的总用电量为125千瓦时,总电费为49元,你知道他家高峰用电量和低谷用电量各是多少千瓦时吗? 2.某瓜果基地生产一种特色水果,若在市场上每吨利润为1000元;经粗加工后销售,每吨利润为4500元;经精加工后销售,每吨利润可达7500元。一食品公司购到这种水果140吨,准备加工后上市销售.该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须将这批水果在15天内全部销售或加工完毕,为此公司研制三种可行的方案:
方案一:将这批水果全部进行粗加工;
方案二:尽可能多对水果进行精加工,没来得及加工的水 果在市场上销售;
方案三:将部分水果进行精加工,其余进行粗加工,并恰好 15天完成.
你认为选择哪种方案获利最多?为什么?课堂小结,知识梳理1.列方程组解应用题的一般步骤2.列表寻找应用题中的等量关系实际问题 数学问题
二元一次方程组 数学问题的解
二元一次方程组的解实际问题
的答案
千里只行四分钟.
归时四分行六百,
风速多少才称雄?顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解:设悟空行走速度是每分钟x里, 风速是每分钟y里,4(x-y)=600 x=200 y=50答:风速是每分钟50里.4(x+y)=1000 解得:依题意得
列方程组解应用题的步骤: 审题
设未知数
列方程组
解方程组
检验
答养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?自主探究1、怎样检验他的估计呢?2、题目中包含怎样的等量关系?这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
你的答案对了吗?解得:205化简得:①②解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg.依题意得
练一练: 长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?解:设应取2米的x段,1米的y段,努力提高自我答:小明估计不准确.2米的应取8段,1米的 应取2段.解得:依题意得努力提高自我 试一试 :某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,x+2y=16802x+y=2280解得:x=960y=360(2)若7个餐厅同时开放,则有
5×960+2×360=5320答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.5320>5300依题意得
想一想 :某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?解:设该公司应安排x天精加工,y天粗加工, x+y=15
6x+16y=140解 得:x=10
y=5答:该公司应安排x10天精加工,5天粗加工.拓展延伸依题意得
哼!我从你背上拿来1个,我的包裹数就是你的2倍!累死我了!你还累?这么大的个,才比我多驮了2个。真的?!谁的包裹多解:设马驮了x个,牛驮了y个,根据题意,得探究一之例3 现有20人生产某种零件,每人每天可以生产螺杆2个或者做螺帽3个, 如果1个螺杆和2个螺帽可以做成一个零件, 那么能否把这 20人分成两部分, 一部分人做螺杆, 一部分人做螺帽,使每天做成的螺杆和螺帽正好配套 ?分析:设x人生产螺杆,则可以生产2x个;
y人生产螺帽,则可以生产3y个。根据题意,得注意:此方程没有整数解如果是28人呢?探究一之例4做一做:1、把长方形纸片折成面积相等的两个小长方形,有哪些折法?2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?●●●● 按面积分割长方形的问题可转化为分割边长的问题。归纳例1:据以往的统计资料,甲、乙两种作物的单位面积产量的比是 1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是 3 : 4 (结果取整数)? 应用数学、解决实际问题甲种作物的总产量 = 甲的单位面积产量×甲的种植面积乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积解:设AE为 x 米,BE为 y 米,由题意得:ABCD●E┓
xy答: 过长方形土地的长边上离一端约106米处,
把这块地分为两个长方形.较大一块地种甲种作
物,较小一块地种乙种作物.ABCD●E┓
yx解:设CE为 x 米,BE为 y 米,由题意得:答: 过长方形土地的短边上离一端约53米处,
把这块地分为两个长方形.较大一块地种甲
种作物,较小一块地种乙种作物. 据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,从长方形边的中点出发引出一条线段怎样把这
块地分为两部分,使甲、乙两种作物的总产量的比是 3 : 4
(结果取整数)? 变式: 例2: 小龙在拼图时,发现8个一样大的小长
方形,恰好可以拼成一个大长方形,如图甲所示,
陈晔看见了说“我来试一试”,结果陈晔七拼八凑,
拼成一个如图乙的正方形,中间留下一个洞,恰
好是边长2mm的小正方形,你能算出小长方形
的长和宽吗?甲乙 例3: 一个长方形,它的长减少4cm,
宽增加2cm,所得的是一个正方形,它的
面积与长方形的面积相等,求原长方形的
长与宽。解:设长方形的长为xcm,宽为ycm,
由题意得:
课前准备:某班文艺小组购买每张3元、5元的杂技票
共计20张,用去76元,问其中3元票、5元
票各几张? 解方程组得: 答:3元票12张,5元票8张。 1、列方程组解应用题的步骤是什么?审:审题,分析题中已知什么,求什么,明确各数量之间的关系 设:设未知数(一般求什么,就设什么为x、y,注意单位) 找:找出能够表示应用题全部意义的两个相等关系 列:根据这两个相等关系列出需要的代数式,进而列出两个方程,
组成方程 解:解所列方程组,得未知数的值 验:检验求得的值是否正确和符合实际情形 答:写出答案(包括单位名称) 2、列方程组解应用题的关键是什么?或者说让大家感觉最难的,最困惑的部分是什么?找到题中的等量关系 如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?审题 2.已知的量:3.要求的量:1.运费的单位“元∕(吨·千米)”的含义 原料从A地运回工厂,每吨运费159元 产品从工厂运到B地,每吨运费162元 铁路、公路运费的单价已知量与未知量的关系原料的铁路运费+原料的公路运费=每吨原料的运费产品的铁路运费+产品的公路运费=每吨产品的运费答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米) 解方程组得:整理方程组得: 探索分析,解决问题例题:(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?设问1.原料的数量与产品的数量一样多吗?(不一样)设问2.那些量设为未知数? 销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .设问3.如何分析题目中的数量关系?能否用列表分析?列表分析:1.5(20X)1.2(110X)1.5(10Y)1.2(120Y)1.5(20X+10Y)1.2(110X+120Y)8000X1000Y由上表可列方程组 解这个方程组,得 :销售款为: 原料费为: 运输费为: 8000X300=2400000(元) 1000X400=400000(元) 15000+97200=112200(元) 所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)答:销售款比原料费与运输费的和多1887800元。 1. 电力行业中峰谷的含义是用山峰和山谷来形象地比喻用电负荷特性的变化幅度一般白天的用电比较集中、用电功率比较大,而夜里人们休息时用电比较小,所以通常白天的用电称为是高峰用电,即8:00~22:00,深夜的用电是低谷用电即22:00~次日8:00.若某地的高峰电价为每千瓦时0.56元;低谷电价为每千瓦时0.28元.八月份小彬家的总用电量为125千瓦时,总电费为49元,你知道他家高峰用电量和低谷用电量各是多少千瓦时吗? 2.某瓜果基地生产一种特色水果,若在市场上每吨利润为1000元;经粗加工后销售,每吨利润为4500元;经精加工后销售,每吨利润可达7500元。一食品公司购到这种水果140吨,准备加工后上市销售.该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须将这批水果在15天内全部销售或加工完毕,为此公司研制三种可行的方案:
方案一:将这批水果全部进行粗加工;
方案二:尽可能多对水果进行精加工,没来得及加工的水 果在市场上销售;
方案三:将部分水果进行精加工,其余进行粗加工,并恰好 15天完成.
你认为选择哪种方案获利最多?为什么?课堂小结,知识梳理1.列方程组解应用题的一般步骤2.列表寻找应用题中的等量关系实际问题 数学问题
二元一次方程组 数学问题的解
二元一次方程组的解实际问题
的答案
