圆柱与圆锥复习课(31页PPT)
图片预览





文档简介
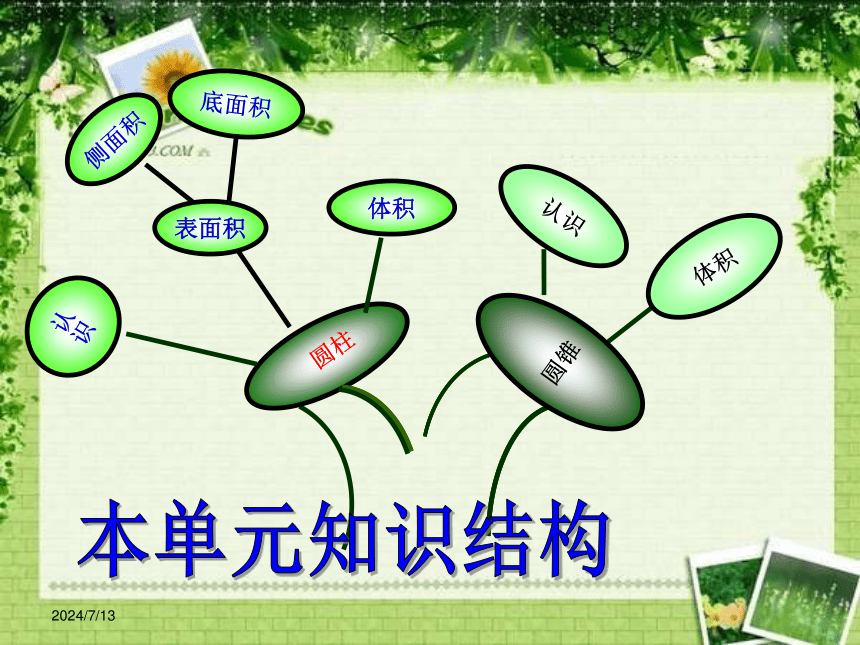
圆柱和圆锥的复习
*
*
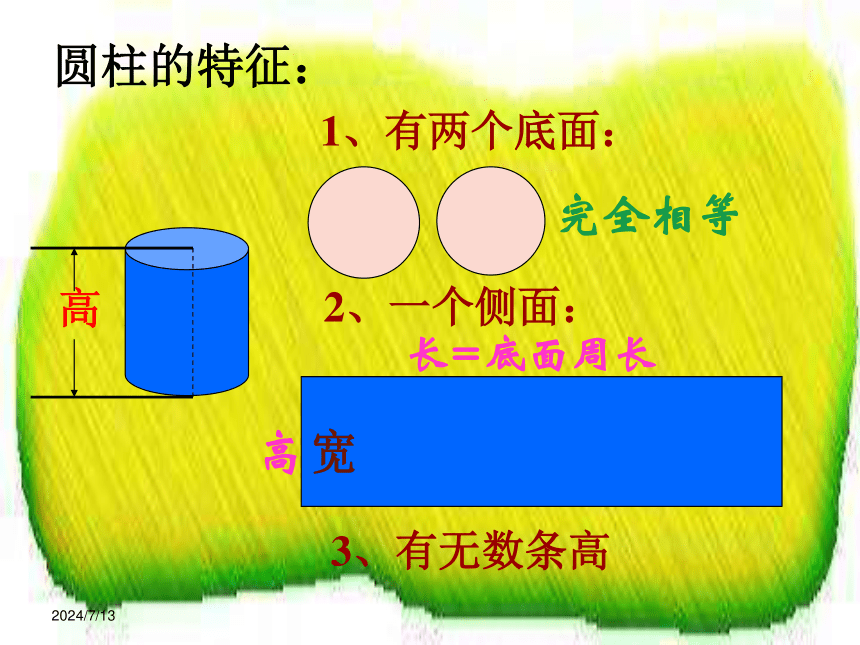
1、有两个底面:
2、一个侧面:
完全相等
高
长=底面周长
圆柱的特征:
宽
3、有无数条高
*
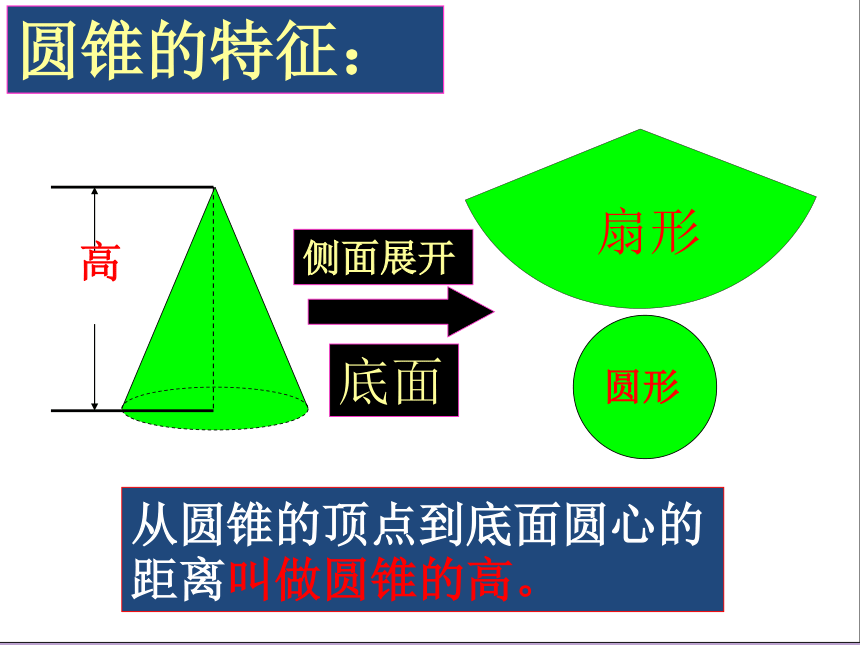
圆锥的特征:
从圆锥的顶点到底面圆心的距离叫做圆锥的高。
*
底面周长×高
侧面积+两个底面积
底面积×高
V=sh
V= sh
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的
等底等高圆柱体积是圆锥体积的3倍
*
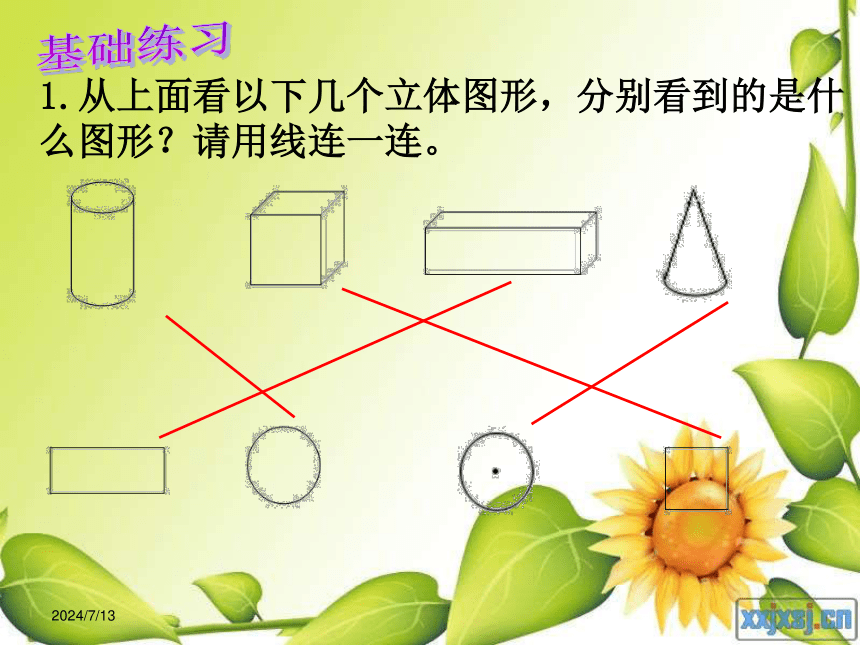
1.从上面看以下几个立体图形,分别看到的是什么图形?请用线连一连。
*
2、说出下列各题与圆柱的哪些知识有关。
做圆柱形烟囱需要多少铁皮。
大厅里圆形柱子的占地面积。
圆柱形水池可蓄多少水。
一根圆柱形的木料有多大。
压路机前轮滚过的面积。
做1个圆柱体需要多少硬纸板。
给圆柱形池塘抹水泥。
(体积)
(容积)
(底面积)
(侧面积)
(侧面积)
(表面积)
(表面积)
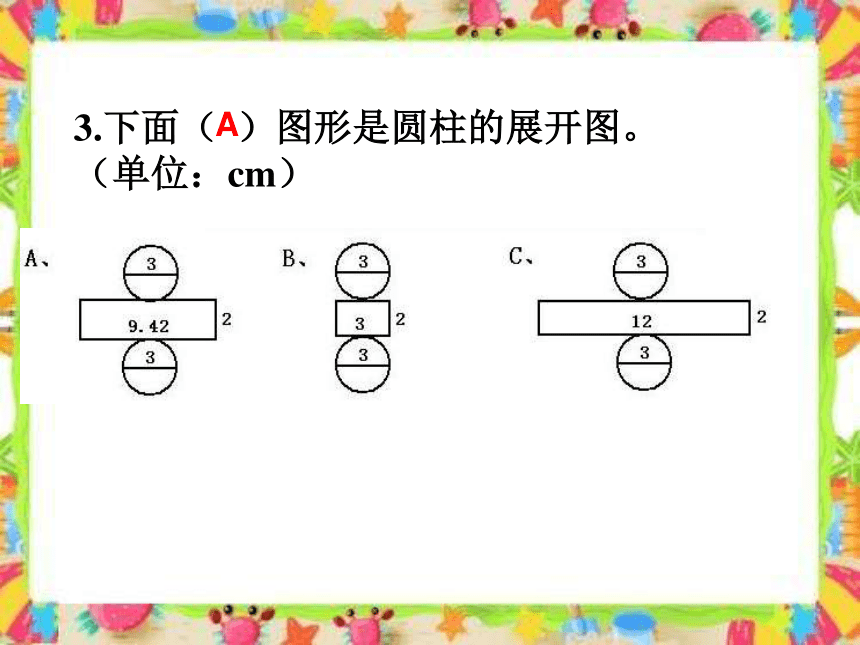
3.下面( )图形是圆柱的展开图。
(单位:cm)
A
45
4、一个圆柱体和一个圆锥体的底面积和高都相等,圆柱的体积是150立方厘米,圆锥的体积是( )立方厘米。
50
5、把一个圆柱体木块削成一个最大的圆锥体,要削去30立方分米,圆柱的体积是( )立方分米。
*
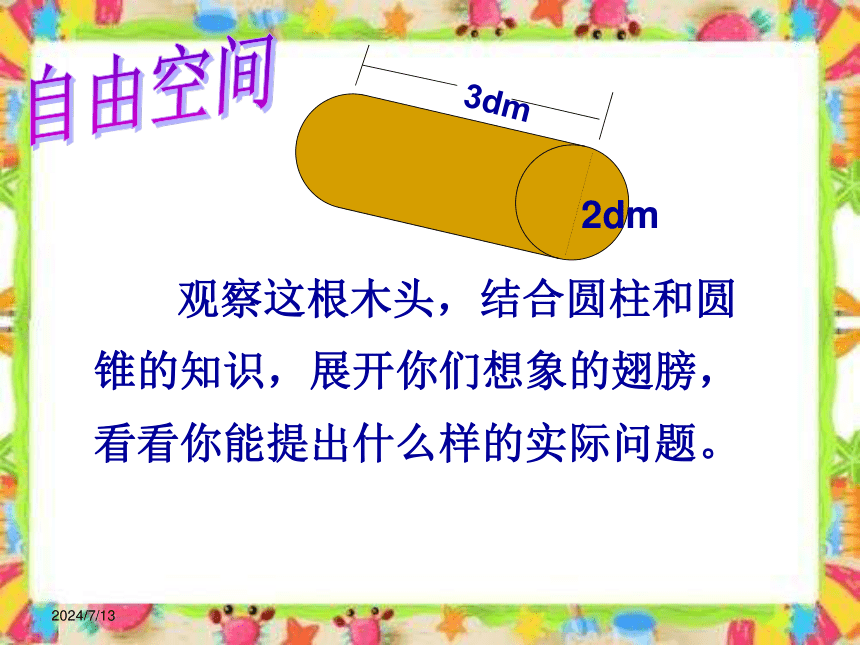
观察这根木头,结合圆柱和圆锥的知识,展开你们想象的翅膀,看看你能提出什么样的实际问题。
*
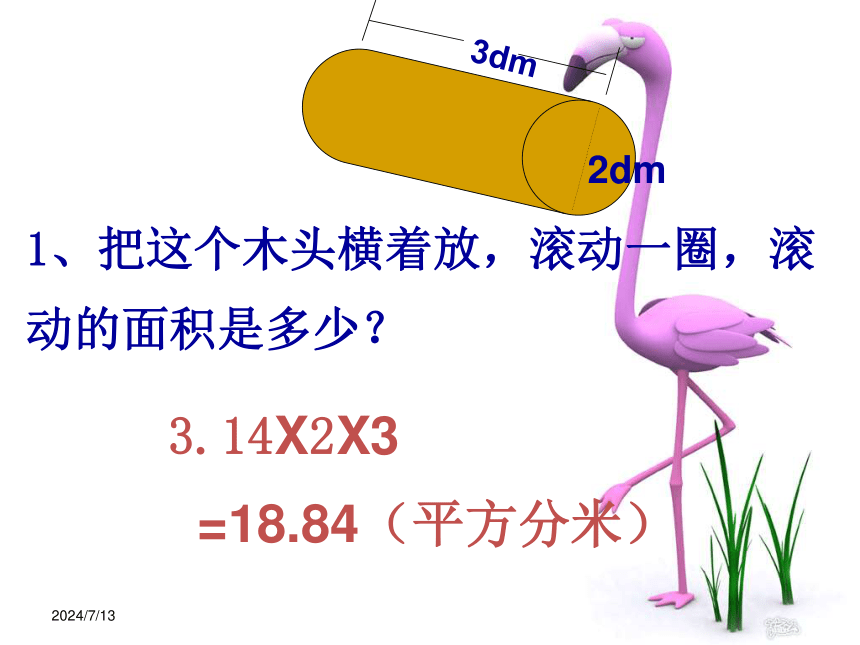
1、把这个木头横着放,滚动一圈,滚动的面积是多少?
3.14X2X3
=18.84(平方分米)
*
2、把这个木头竖着放,它的占地面积是多少?
2÷2=1(cm)
3.14X1X1
=3.14(平方分米)
*
3、把这根木头全都刷上油漆,刷油漆的面积有多大?
3.14X2X3+ 3.14X 12 X2
=18.84 + 6.28
=25.12(平方分米)
*
4、这个木头的体积是多少?
3.14X( 2÷2 )2 X3
=3.14 X3
=9.42(立方分米)
*
5、如果沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少 ?
2X3X2
=6X2
=12(平方分米)
*
6、把这个圆柱切成四段,它的表面积增加了多少?
3.14X12 X6=18.84(平方分米)
7、如果切去4厘米高的一截,它的表面积会减少多少呢?
3.14X2X0.4=2.512(平方分米)
8、如果把这个圆柱形的木头削成最大的圆锥,这个圆锥的体积是多少?削去的体积是多少?
*
=3.14 X1
=3.14(立方分米)
3.14X2=6.28(立方分米)
3.14X12 X3X
*
9.如果把削成的这个最大的圆锥沿顶点垂直底面切开,表面积会增加多少?
2X3÷2X2=6(平方分米)
2dm
*
10、如果把这个圆柱变成一个圆锥,体积和底面积都相等,那么这个圆锥的高是多少?
3X3=9(分米)
*
11、如果这个圆柱与一个圆锥的体积和高相等,那么这个圆锥的底面积是多少?
3.14X12 X3=9.42(平方分米)
*
12、如果把这根木头让它浮在水面上,正好一半露出水面,这根木头与水接触面的面积是多少?木头浸没在水中体积是多少?
3.14X12 X3÷2=4.71(立方分米)
3.14X12 +3.14X2X3÷2=12.56(平方分米)
1.学校用的自来水管内直径为0.2分米,自来水的流速,一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费多少升水?
?
节约用水是我们每个小学生的义务,
2.一个粮仓如右图,如果每立方米粮食重400千克,这个粮仓最多能装多少吨粮食?
3.把一个棱长是6厘米的正方体木块,削成一个最大的圆锥体,圆锥的体积是多少立方厘米?
4.在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
思考题
如图,想想办法,你能否求它的体积?( 单位:厘米)
2
4
6
6
4
2
思考题
如图,想想办法,你能否求它的体积?( 单位:厘米)
2
4
6
6
4
2
3.14X12X(4+6)÷2
=15.7(立方厘米)
2÷2=1(厘米)
*
知识回顾:
本节课你有何收获?
*
*
1、有两个底面:
2、一个侧面:
完全相等
高
长=底面周长
圆柱的特征:
宽
3、有无数条高
*
圆锥的特征:
从圆锥的顶点到底面圆心的距离叫做圆锥的高。
*
底面周长×高
侧面积+两个底面积
底面积×高
V=sh
V= sh
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的
等底等高圆柱体积是圆锥体积的3倍
*
1.从上面看以下几个立体图形,分别看到的是什么图形?请用线连一连。
*
2、说出下列各题与圆柱的哪些知识有关。
做圆柱形烟囱需要多少铁皮。
大厅里圆形柱子的占地面积。
圆柱形水池可蓄多少水。
一根圆柱形的木料有多大。
压路机前轮滚过的面积。
做1个圆柱体需要多少硬纸板。
给圆柱形池塘抹水泥。
(体积)
(容积)
(底面积)
(侧面积)
(侧面积)
(表面积)
(表面积)
3.下面( )图形是圆柱的展开图。
(单位:cm)
A
45
4、一个圆柱体和一个圆锥体的底面积和高都相等,圆柱的体积是150立方厘米,圆锥的体积是( )立方厘米。
50
5、把一个圆柱体木块削成一个最大的圆锥体,要削去30立方分米,圆柱的体积是( )立方分米。
*
观察这根木头,结合圆柱和圆锥的知识,展开你们想象的翅膀,看看你能提出什么样的实际问题。
*
1、把这个木头横着放,滚动一圈,滚动的面积是多少?
3.14X2X3
=18.84(平方分米)
*
2、把这个木头竖着放,它的占地面积是多少?
2÷2=1(cm)
3.14X1X1
=3.14(平方分米)
*
3、把这根木头全都刷上油漆,刷油漆的面积有多大?
3.14X2X3+ 3.14X 12 X2
=18.84 + 6.28
=25.12(平方分米)
*
4、这个木头的体积是多少?
3.14X( 2÷2 )2 X3
=3.14 X3
=9.42(立方分米)
*
5、如果沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少 ?
2X3X2
=6X2
=12(平方分米)
*
6、把这个圆柱切成四段,它的表面积增加了多少?
3.14X12 X6=18.84(平方分米)
7、如果切去4厘米高的一截,它的表面积会减少多少呢?
3.14X2X0.4=2.512(平方分米)
8、如果把这个圆柱形的木头削成最大的圆锥,这个圆锥的体积是多少?削去的体积是多少?
*
=3.14 X1
=3.14(立方分米)
3.14X2=6.28(立方分米)
3.14X12 X3X
*
9.如果把削成的这个最大的圆锥沿顶点垂直底面切开,表面积会增加多少?
2X3÷2X2=6(平方分米)
2dm
*
10、如果把这个圆柱变成一个圆锥,体积和底面积都相等,那么这个圆锥的高是多少?
3X3=9(分米)
*
11、如果这个圆柱与一个圆锥的体积和高相等,那么这个圆锥的底面积是多少?
3.14X12 X3=9.42(平方分米)
*
12、如果把这根木头让它浮在水面上,正好一半露出水面,这根木头与水接触面的面积是多少?木头浸没在水中体积是多少?
3.14X12 X3÷2=4.71(立方分米)
3.14X12 +3.14X2X3÷2=12.56(平方分米)
1.学校用的自来水管内直径为0.2分米,自来水的流速,一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费多少升水?
?
节约用水是我们每个小学生的义务,
2.一个粮仓如右图,如果每立方米粮食重400千克,这个粮仓最多能装多少吨粮食?
3.把一个棱长是6厘米的正方体木块,削成一个最大的圆锥体,圆锥的体积是多少立方厘米?
4.在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
思考题
如图,想想办法,你能否求它的体积?( 单位:厘米)
2
4
6
6
4
2
思考题
如图,想想办法,你能否求它的体积?( 单位:厘米)
2
4
6
6
4
2
3.14X12X(4+6)÷2
=15.7(立方厘米)
2÷2=1(厘米)
*
知识回顾:
本节课你有何收获?
