7.2.6总复习 立体图形的表面积和体积(一) 课件(16张ppt)
文档属性
| 名称 | 7.2.6总复习 立体图形的表面积和体积(一) 课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-15 00:00:00 | ||
图片预览

文档简介
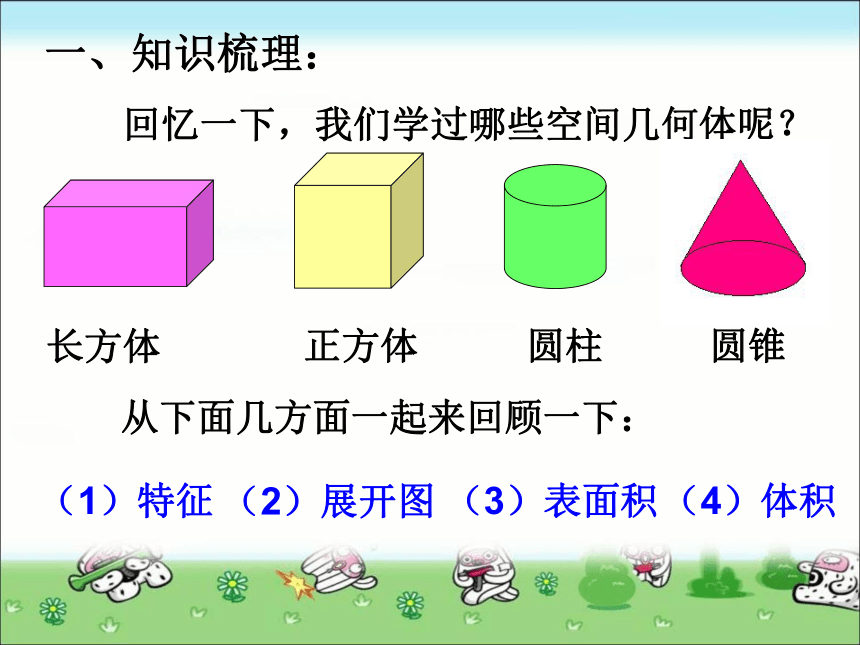
课件16张PPT。 立体图形的表面积和体积复习 回忆一下,我们学过哪些空间几何体呢?一、知识梳理:长方体正方体圆柱圆锥(2)展开图(3)表面积(4)体积(1)特征从下面几方面一起来回顾一下:8个6个12
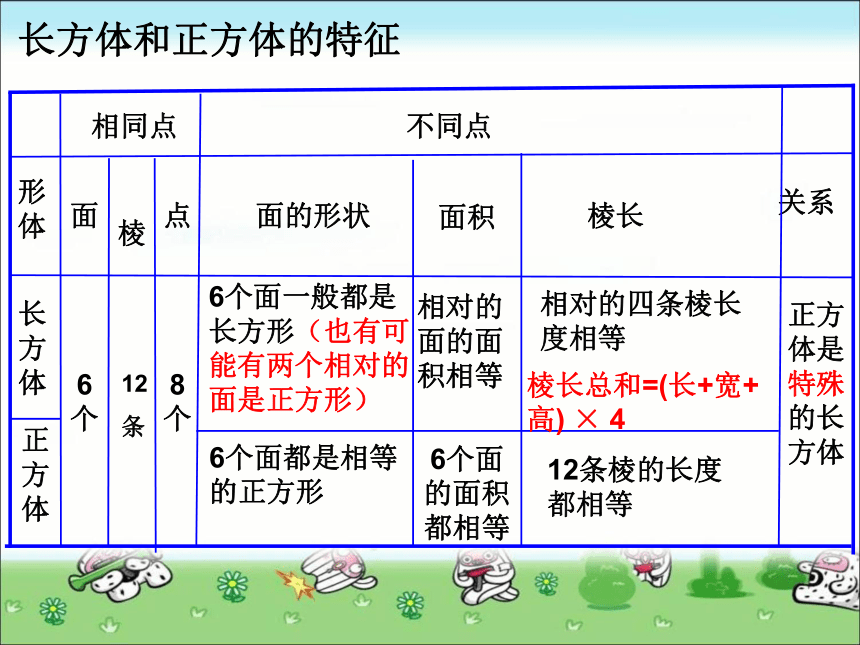
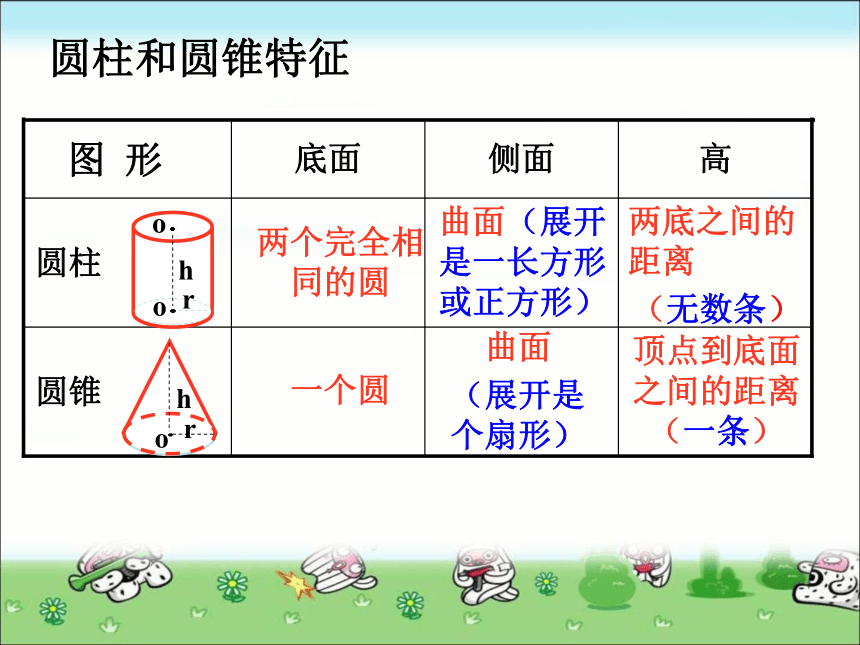
条6个面一般都是长方形(也有可能有两个相对的面是正方形)相对的面的面积相等相对的四条棱长度相等6个面都是相等的正方形6个面的面积都相等12条棱的长度都相等正方体是特殊的长方体棱长总和=(长+宽+高) × 4长方体和正方体的特征圆柱和圆锥特征圆锥圆柱高侧面底面图 形曲面
(展开是个扇形)一个圆两底之间的距离
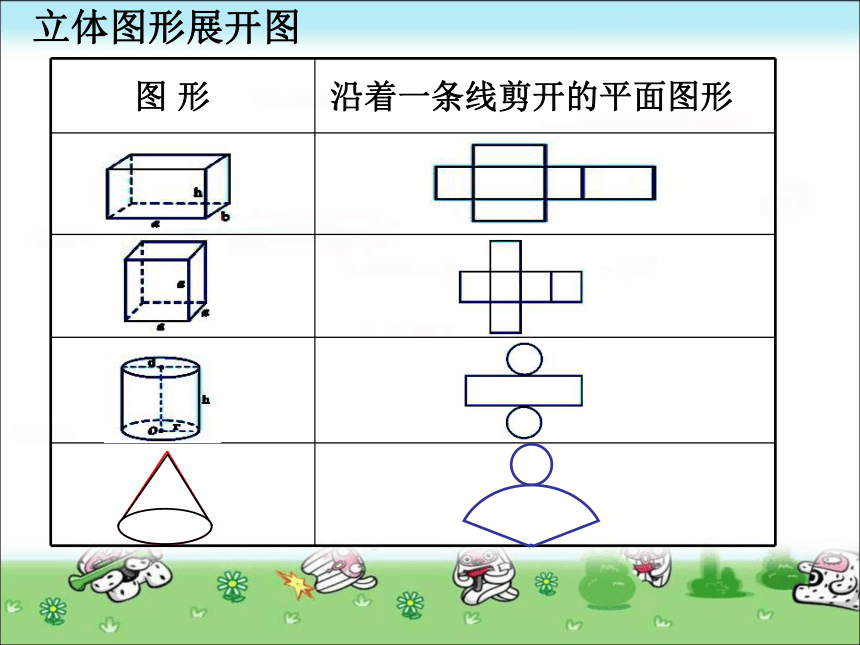
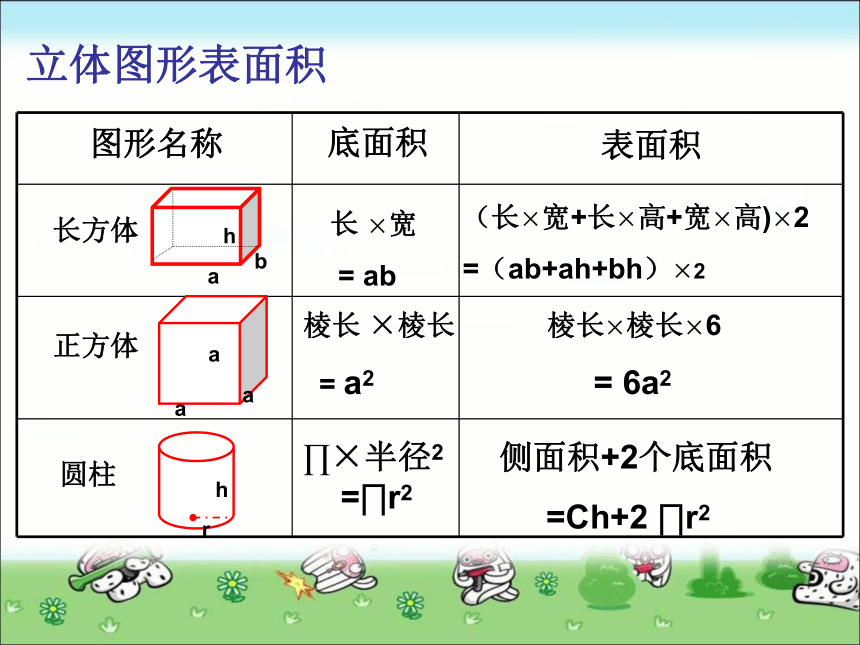
(无数条)曲面(展开是一长方形或正方形)两个完全相同的圆顶点到底面之间的距离(一条)立体图形展开图图 形沿着一条线剪开的平面图形立体图形表面积图形名称底面积表面积长方体abh长 ×宽
= ab (长×宽+长×高+宽×高)×2
=(ab+ah+bh)×2正方体棱长 ×棱长
= a2棱长×棱长×6
= 6a2圆柱侧面积+2个底面积
=Ch+2 ∏r2∏×半径2
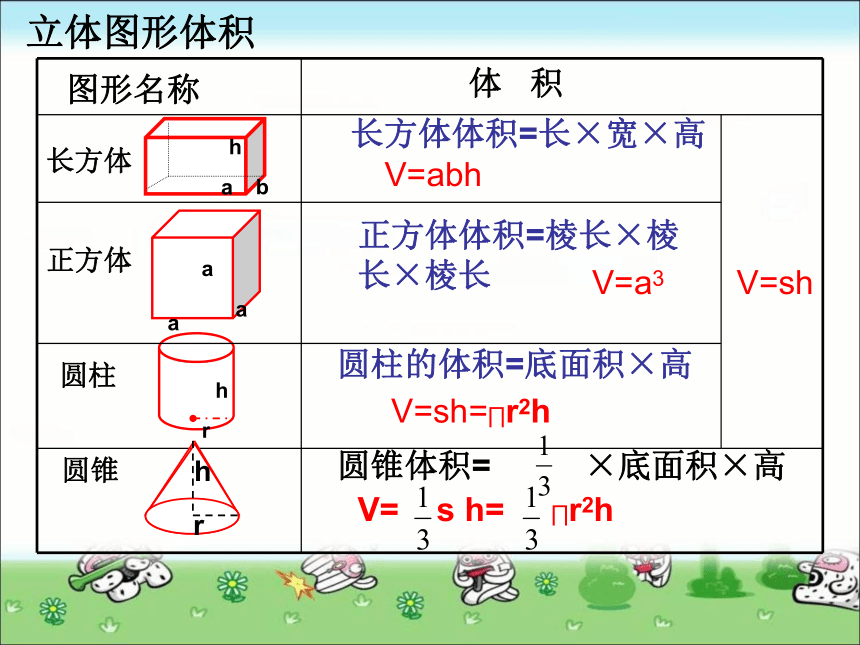
=∏r2立体图形体积图形名称长方体正方体圆柱abhrh长方体体积=长×宽×高V=abh正方体体积=棱长×棱长×棱长 V=a3V=sh圆柱的体积=底面积×高V=sh=∏r2h
(一)填空1、把圆柱的侧面沿高展开,一般可以得到 ( ) 形,这个图形的长相当于( ),宽相当于( )。
2、用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( )厘米。
3、一个长方体最多可以有( )个面是正方形。二、基础练习4、一个 正方体的底面周长是4分米,它的表面积是( ),体积是 ( )。5、一个圆柱和圆锥的体积相等,底面积也相等。圆柱和圆锥的高的比是( )长方形底面圆的周长圆柱的高6026平方分米1立方分米1:3(二)口答(1)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸, 求商标纸的面积是求( ) 。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3)下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的( )。表面积侧面积侧面积侧面积(4)做一个长方体木箱框架,至少需要多少木条,是求它的( );在周围封上木板,至少需要多少木板,是求它的( );求它的占地面积,是求( );求它所占的空间大小,是求( );求他能容纳多少物体,是求( )。
棱长总和表面积底面积体积容积(三)想想,做做1.把一个长4厘米、宽3厘米、高2厘米的长方体,截成两个长方体,表面积最多增加多少?最少呢?3. 把 底面半径2厘米,高5厘米的圆柱 横截、纵截(沿底面直径) ,表面积分别增加了多少平方厘米?4.把底面半径2厘米,高5厘米的圆锥沿着高纵截成两部分,表面积增加了多少平方厘米?
2. 把4个棱长1厘米的正方体拼成一个长方体,表面积、体积发生变化吗?拼成的长方体表面积是多少?4.把底面半径2厘米,高5厘米的圆锥沿着高纵截成两部分,表面积增加了多少平方厘米?三、提升训练1、化工厂计划在长10米宽8米的长方形空地上挖一个尽可能大的圆柱水池。如果挖成的水池深5米。那么这个水池能蓄水多少立方米?10米8米3、把一个圆锥形铁块浸没在一个底面半径是6厘米,水深30厘米的圆柱形容器中,水面上升到32米。这个圆锥形铁块的体积是多少?2、把一个底面直径6分米、高4分米的圆锥形零件熔铸成一个底面直径是4分米的圆柱形零件,求圆柱零件的高。变化:
把一个底面直径6分米、高4分米的圆柱形零件熔铸成一个底面直径是4分米的圆锥形零件,求圆柱零件的高。探讨:下面的直角三角形,以一条直角边为轴旋转一周,可以形成什么样的几何体?它的体积是多少?3cm4cm5cm(1)比较旋转后所得的几何体的大小,你发现了什么?(2)不计算,你能比较他们的大小吗?(3)如果以斜边为轴旋转一周,可以形成什么样的几何体?讨论:尝试:你能计算它的体积吗?将一张长94.2厘米、宽62.8厘米的铁皮,圈成圆柱形状,再配上一个底面,想一想,怎样才能制成一个容积最大的油桶?思考:
条6个面一般都是长方形(也有可能有两个相对的面是正方形)相对的面的面积相等相对的四条棱长度相等6个面都是相等的正方形6个面的面积都相等12条棱的长度都相等正方体是特殊的长方体棱长总和=(长+宽+高) × 4长方体和正方体的特征圆柱和圆锥特征圆锥圆柱高侧面底面图 形曲面
(展开是个扇形)一个圆两底之间的距离
(无数条)曲面(展开是一长方形或正方形)两个完全相同的圆顶点到底面之间的距离(一条)立体图形展开图图 形沿着一条线剪开的平面图形立体图形表面积图形名称底面积表面积长方体abh长 ×宽
= ab (长×宽+长×高+宽×高)×2
=(ab+ah+bh)×2正方体棱长 ×棱长
= a2棱长×棱长×6
= 6a2圆柱侧面积+2个底面积
=Ch+2 ∏r2∏×半径2
=∏r2立体图形体积图形名称长方体正方体圆柱abhrh长方体体积=长×宽×高V=abh正方体体积=棱长×棱长×棱长 V=a3V=sh圆柱的体积=底面积×高V=sh=∏r2h
(一)填空1、把圆柱的侧面沿高展开,一般可以得到 ( ) 形,这个图形的长相当于( ),宽相当于( )。
2、用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( )厘米。
3、一个长方体最多可以有( )个面是正方形。二、基础练习4、一个 正方体的底面周长是4分米,它的表面积是( ),体积是 ( )。5、一个圆柱和圆锥的体积相等,底面积也相等。圆柱和圆锥的高的比是( )长方形底面圆的周长圆柱的高6026平方分米1立方分米1:3(二)口答(1)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸, 求商标纸的面积是求( ) 。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3)下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的( )。表面积侧面积侧面积侧面积(4)做一个长方体木箱框架,至少需要多少木条,是求它的( );在周围封上木板,至少需要多少木板,是求它的( );求它的占地面积,是求( );求它所占的空间大小,是求( );求他能容纳多少物体,是求( )。
棱长总和表面积底面积体积容积(三)想想,做做1.把一个长4厘米、宽3厘米、高2厘米的长方体,截成两个长方体,表面积最多增加多少?最少呢?3. 把 底面半径2厘米,高5厘米的圆柱 横截、纵截(沿底面直径) ,表面积分别增加了多少平方厘米?4.把底面半径2厘米,高5厘米的圆锥沿着高纵截成两部分,表面积增加了多少平方厘米?
2. 把4个棱长1厘米的正方体拼成一个长方体,表面积、体积发生变化吗?拼成的长方体表面积是多少?4.把底面半径2厘米,高5厘米的圆锥沿着高纵截成两部分,表面积增加了多少平方厘米?三、提升训练1、化工厂计划在长10米宽8米的长方形空地上挖一个尽可能大的圆柱水池。如果挖成的水池深5米。那么这个水池能蓄水多少立方米?10米8米3、把一个圆锥形铁块浸没在一个底面半径是6厘米,水深30厘米的圆柱形容器中,水面上升到32米。这个圆锥形铁块的体积是多少?2、把一个底面直径6分米、高4分米的圆锥形零件熔铸成一个底面直径是4分米的圆柱形零件,求圆柱零件的高。变化:
把一个底面直径6分米、高4分米的圆柱形零件熔铸成一个底面直径是4分米的圆锥形零件,求圆柱零件的高。探讨:下面的直角三角形,以一条直角边为轴旋转一周,可以形成什么样的几何体?它的体积是多少?3cm4cm5cm(1)比较旋转后所得的几何体的大小,你发现了什么?(2)不计算,你能比较他们的大小吗?(3)如果以斜边为轴旋转一周,可以形成什么样的几何体?讨论:尝试:你能计算它的体积吗?将一张长94.2厘米、宽62.8厘米的铁皮,圈成圆柱形状,再配上一个底面,想一想,怎样才能制成一个容积最大的油桶?思考:
