【鲁教版八下精美学案】第九章 图形的相似 章末复习(知识构建+考点归纳+真题训练)
文档属性
| 名称 | 【鲁教版八下精美学案】第九章 图形的相似 章末复习(知识构建+考点归纳+真题训练) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-16 00:00:00 | ||
图片预览




文档简介
第九章 图形的相似
章 末 复 习
考点归纳
考点1: 成比例线段
1.下列四条线段能成比例线段的是( )
A.1,1,2,3 B.1,2,3,4 C.2,2,3,3 D.2,3,4,5
2.已知,那么下列等式中,不成立的是( )
A. B. C. D.4x=3y
考点2: 平行线分线段成比
3.如图所示,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB:BC=1:2,DE=3,则EF的长为____________。
4.如图所示,已知△ABC中,DE∥BC, AD=5, EC=2, BD=AE=x,求BD的长。
考点3: 相似多边形
5.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
6.如图所示,一个矩形广场的长为60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?
考点4: 探索三角形相似的条件
7.已知:如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
8.已知:如图所示,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E,F。
(1)求证:EF=AE-BE;
(2)连接BF,如果。求证:EF=EP。
考点5: 黄金分割
9.如果C是线段AB一点,并且AC>CB,AB=1,那么AC的长度为_______时,点C是线段AB的黄金分割点( )
A.0.618 B. C. D.
10.主持人主持节目时,站在舞台的黄金分割点处最自然得体。如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走_______米才最理想.( )
A.18-6 B.6-6 C.6+6 D.18-6或6-6
考点6: 利用相似三角形测高
11.(2018·长春)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
12.如图所示,某水平地面上有建筑物AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,使点G与建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,使点H与建筑物顶点A和标杆顶端E在同一条直线上,则建筑物的高是_________米。
13.如图所示,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( )
A.8.5米 B.9米 C.9.5米 D.10米
考点7: 相似三角形的性质
14.已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
15.如图所示,在 ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A. B. C. D.
考点8: 利用位似放缩图形
16.如图所示是△ABC位似图形的几种画法,其中正确的个数是( )
A.1 B.2 C.3 D.4
17.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
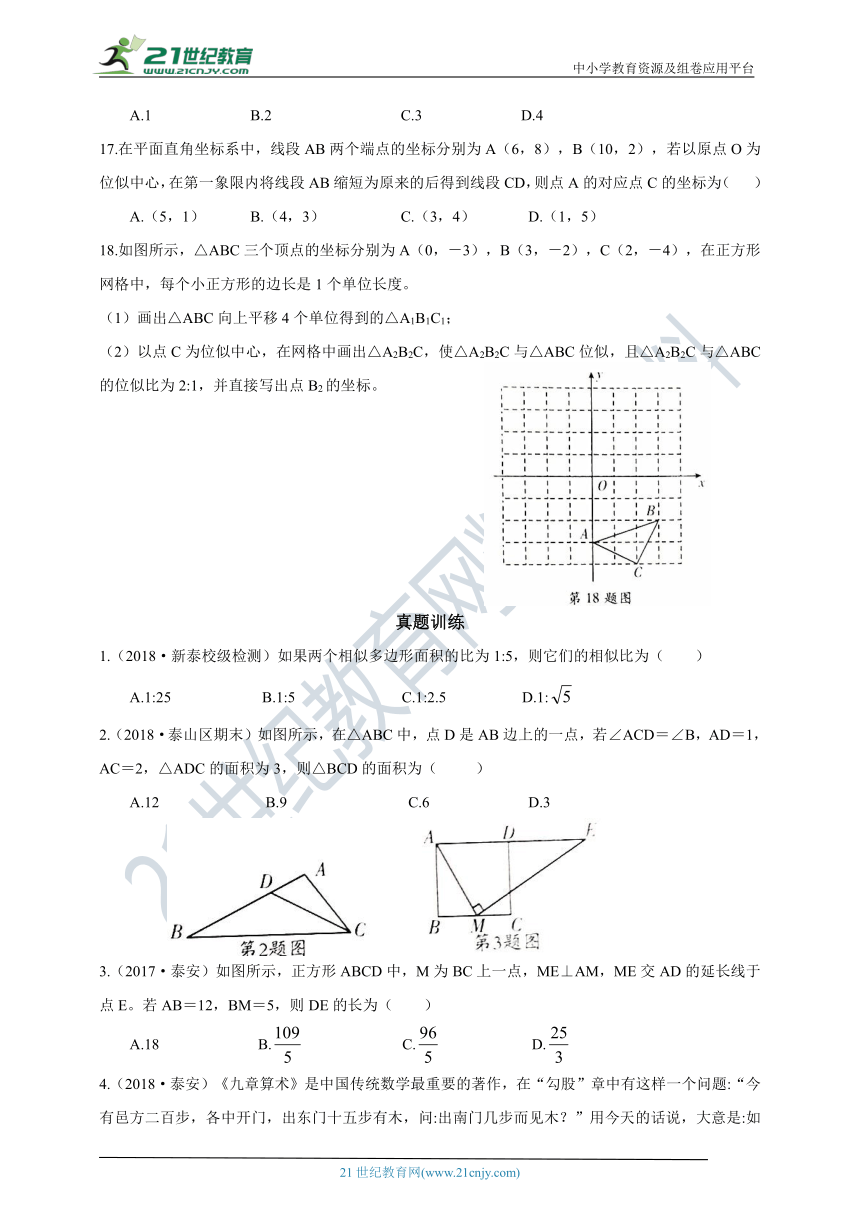
18.如图所示,△ABC三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4),在正方形网格中,每个小正方形的边长是1个单位长度。
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标。
真题训练
1.(2018·新泰校级检测)如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A.1:25 B.1:5 C.1:2.5 D.1:
2.(2018·泰山区期末)如图所示,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,
AC=2,△ADC的面积为3,则△BCD的面积为( )
A.12 B.9 C.6 D.3
3.(2017·泰安)如图所示,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E。若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
4.(2018·泰安)《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图所示,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为_________步。
5.(2014·泰安)如图所示,在四边形ABCD中AB=AD,AC与BD交于点E,∠ADB=∠ACB。(1)求证:;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形。
6.(2015·泰安)如图所示,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B。
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长。
7.(2016·泰安)如图所示,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE。
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB。
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形。
8.(2017·泰安)如图所示,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD。
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长。
9.(2018·泰安)如图所示,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF∥AB,
∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G。
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与△AGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF·MH。
10.(2018·宁夏)已知:△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5)。(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标。
参考答案及解析
考点归纳
1.C 2.B 3.6
4.解:∵DE∥BC,∴,∴,∴x2=10。
x=或x=-(舍去)。∴BD=。
D
6.解:∵小路内外边缘所围成的两个矩形相似,
∴,解得,x=1m。
答:当x为1m时,小路内外边缘所围成的两个矩形相似。
7. D
8.证明:(1)∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°。
∵BE⊥AP,DF⊥AP,∴∠BEA=∠AFD=90°。
∴∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3。
在△ABE和△DAF中,,∴△ABE≌△DAF,∴BE=AF,
∴EF=AE-AF=AE-BE;
(2)如图所示,∵,而AF=BE,∴,∴。
∴Rt△BEF∽RtA△DFA。∴∠4=∠3,而∠1=∠3.∴∠4=∠1。
∵∠5=∠1,∴∠4=∠5。即BE平分∠FBP,而BE⊥EP,∴EF=EP。
9.C 10.A 11.B 12.54 13.A 14.A 15.D 16.D 17.C
18.解:(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C为所求三角形,点B2的坐标为(4,0)。
真题训练
1.D 2.B 3.B 4.
5.证明:(1)∵AB=AD,∴∠ADB=∠ABE。又∵∠ADB=∠ACB,∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,∴△ABE∽△ACB。∴。
又∵B=AD,∴。
(2)设AE=x,∵AE:EC=1:2,∴EC=2x,
由(1)得:AB2=AE?AC,即AB2=x?3x.AB=x。
又∵BA⊥AC,∴BC=2 x,∴∠ACB=30°,
∵F是BC中点,∴BF=x,∴BF=AB=AD。
连接AF,则AF=BF=CF,∠ACB=30°,∠ABC=60o。
又∵∠ABD=∠ADB=30°,∴∠CBD=30°,∴∠ADB=∠CBD=∠ACB=30°,
∴AD∥BF,∵四边形ABFD是平行四边形。又∵AD=AB,
∴四边形ABFD是菱形。
6.解:(1)证明:∵AB=AC,∠B=∠C。∴∠APD=∠B,∴∠APD=∠B=∠C。
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC。
∴△ABP∽△PCD,∴,∴AB?CD=CP?BP。
∵AB=AC,∴AC?CD=CP?BP。
(2)∵PD∥AB,∴∠APD=∠BAP,∵∠APD=∠C,∠BAP=∠C。
又∵∠B=∠B,∴△BAP∽△BCA,∴。
∵AB=10,BC=12,∴,∴BP=。
7.证明:(1)∵AC平分∠BCD,∴∠DCA=∠ACB。
又∵AC⊥AB,AD⊥AE,∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB。又∵E是BC的中点,∴AE=BE。
∴∠EAB=∠ABC,∴∠DAC=∠ABC,∴△ACD∽△BCA,∴。
∴AC2=CD?BC;
(2)①证明:连接AH。
∵∠ADC=∠BAC=90o,点H,D关于AC对称,∴AH⊥BC。
∵EG⊥AB,AE=BE,∴点G是AB的中点,∴HG=AG,∴∠GAH=∠GHA。
∵点F为AC的中点,∴AF=FH,∴∠HAF=∠FHA,
∴∠FHG=∠AHF+∠AHG=∠FAH+∠HAG=∠CAB=90°,∴FH⊥GH;
②EK⊥AB,AC⊥AB,∴EK∥AC。又∵∠B=30°,
∴ AC=BC=EB=EC。又EK=EB,∴EK=AC,即AK=KE=EC=CA,∴四边形AKEC是菱形。
8.解:(1)证明:AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90o。
∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90o。
∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC。
(2)过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM。
∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴。
设CM=CE=x,∵CE:CP=2:3,∴PC=。∵AB=AD=AC=1,
∴,解得:x=,故AE=1-=。
9.解:(1)∠DEF=∠AEF。
理由:∵EF∥AB,∴∠DEF=∠EBA,∠AEF=∠EAB,
∵∠EAB=∠EBA,∴∠DEF=∠AEF;
(2)△EOA∽△AGB,
理由:∵四边形ABCD是菱形,∴AB=AD,AC⊥BD,
∴∠GAB=∠ABE+∠ADB=2∠ABE.∵∠AEO=∠ABE+∠BAE=2∠ABE,
∴∠GAB=∠AEO。∵∠AGB=∠AOE=90o,∴△EOA∽△AGB;
(3)证明:如图所示,连接DM。
∵四边形ABCD是菱形,∴由对称性可知,BM=DM,∠ADM=∠ABM.
∵AB∥CH,∴∠ABM=∠H,∴∠ADM=∠H,∵∠DMH=∠FMD,
∴△MFD∽△MDH,∴,
∴DM2=MF·MH,∴BM2=MF·MH。
10.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
B2(10,8)。
章 末 复 习
考点归纳
考点1: 成比例线段
1.下列四条线段能成比例线段的是( )
A.1,1,2,3 B.1,2,3,4 C.2,2,3,3 D.2,3,4,5
2.已知,那么下列等式中,不成立的是( )
A. B. C. D.4x=3y
考点2: 平行线分线段成比
3.如图所示,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB:BC=1:2,DE=3,则EF的长为____________。
4.如图所示,已知△ABC中,DE∥BC, AD=5, EC=2, BD=AE=x,求BD的长。
考点3: 相似多边形
5.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
6.如图所示,一个矩形广场的长为60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为x m,那么当x为多少时,小路内外边缘所围成的两个矩形相似?
考点4: 探索三角形相似的条件
7.已知:如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
8.已知:如图所示,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E,F。
(1)求证:EF=AE-BE;
(2)连接BF,如果。求证:EF=EP。
考点5: 黄金分割
9.如果C是线段AB一点,并且AC>CB,AB=1,那么AC的长度为_______时,点C是线段AB的黄金分割点( )
A.0.618 B. C. D.
10.主持人主持节目时,站在舞台的黄金分割点处最自然得体。如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走_______米才最理想.( )
A.18-6 B.6-6 C.6+6 D.18-6或6-6
考点6: 利用相似三角形测高
11.(2018·长春)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
12.如图所示,某水平地面上有建筑物AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,使点G与建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,使点H与建筑物顶点A和标杆顶端E在同一条直线上,则建筑物的高是_________米。
13.如图所示,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( )
A.8.5米 B.9米 C.9.5米 D.10米
考点7: 相似三角形的性质
14.已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
15.如图所示,在 ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A. B. C. D.
考点8: 利用位似放缩图形
16.如图所示是△ABC位似图形的几种画法,其中正确的个数是( )
A.1 B.2 C.3 D.4
17.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
18.如图所示,△ABC三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4),在正方形网格中,每个小正方形的边长是1个单位长度。
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标。
真题训练
1.(2018·新泰校级检测)如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A.1:25 B.1:5 C.1:2.5 D.1:
2.(2018·泰山区期末)如图所示,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,
AC=2,△ADC的面积为3,则△BCD的面积为( )
A.12 B.9 C.6 D.3
3.(2017·泰安)如图所示,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E。若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
4.(2018·泰安)《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图所示,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为_________步。
5.(2014·泰安)如图所示,在四边形ABCD中AB=AD,AC与BD交于点E,∠ADB=∠ACB。(1)求证:;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形。
6.(2015·泰安)如图所示,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B。
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长。
7.(2016·泰安)如图所示,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE。
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB。
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形。
8.(2017·泰安)如图所示,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD。
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长。
9.(2018·泰安)如图所示,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF∥AB,
∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G。
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与△AGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF·MH。
10.(2018·宁夏)已知:△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5)。(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标。
参考答案及解析
考点归纳
1.C 2.B 3.6
4.解:∵DE∥BC,∴,∴,∴x2=10。
x=或x=-(舍去)。∴BD=。
D
6.解:∵小路内外边缘所围成的两个矩形相似,
∴,解得,x=1m。
答:当x为1m时,小路内外边缘所围成的两个矩形相似。
7. D
8.证明:(1)∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°。
∵BE⊥AP,DF⊥AP,∴∠BEA=∠AFD=90°。
∴∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3。
在△ABE和△DAF中,,∴△ABE≌△DAF,∴BE=AF,
∴EF=AE-AF=AE-BE;
(2)如图所示,∵,而AF=BE,∴,∴。
∴Rt△BEF∽RtA△DFA。∴∠4=∠3,而∠1=∠3.∴∠4=∠1。
∵∠5=∠1,∴∠4=∠5。即BE平分∠FBP,而BE⊥EP,∴EF=EP。
9.C 10.A 11.B 12.54 13.A 14.A 15.D 16.D 17.C
18.解:(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C为所求三角形,点B2的坐标为(4,0)。
真题训练
1.D 2.B 3.B 4.
5.证明:(1)∵AB=AD,∴∠ADB=∠ABE。又∵∠ADB=∠ACB,∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,∴△ABE∽△ACB。∴。
又∵B=AD,∴。
(2)设AE=x,∵AE:EC=1:2,∴EC=2x,
由(1)得:AB2=AE?AC,即AB2=x?3x.AB=x。
又∵BA⊥AC,∴BC=2 x,∴∠ACB=30°,
∵F是BC中点,∴BF=x,∴BF=AB=AD。
连接AF,则AF=BF=CF,∠ACB=30°,∠ABC=60o。
又∵∠ABD=∠ADB=30°,∴∠CBD=30°,∴∠ADB=∠CBD=∠ACB=30°,
∴AD∥BF,∵四边形ABFD是平行四边形。又∵AD=AB,
∴四边形ABFD是菱形。
6.解:(1)证明:∵AB=AC,∠B=∠C。∴∠APD=∠B,∴∠APD=∠B=∠C。
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC。
∴△ABP∽△PCD,∴,∴AB?CD=CP?BP。
∵AB=AC,∴AC?CD=CP?BP。
(2)∵PD∥AB,∴∠APD=∠BAP,∵∠APD=∠C,∠BAP=∠C。
又∵∠B=∠B,∴△BAP∽△BCA,∴。
∵AB=10,BC=12,∴,∴BP=。
7.证明:(1)∵AC平分∠BCD,∴∠DCA=∠ACB。
又∵AC⊥AB,AD⊥AE,∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB。又∵E是BC的中点,∴AE=BE。
∴∠EAB=∠ABC,∴∠DAC=∠ABC,∴△ACD∽△BCA,∴。
∴AC2=CD?BC;
(2)①证明:连接AH。
∵∠ADC=∠BAC=90o,点H,D关于AC对称,∴AH⊥BC。
∵EG⊥AB,AE=BE,∴点G是AB的中点,∴HG=AG,∴∠GAH=∠GHA。
∵点F为AC的中点,∴AF=FH,∴∠HAF=∠FHA,
∴∠FHG=∠AHF+∠AHG=∠FAH+∠HAG=∠CAB=90°,∴FH⊥GH;
②EK⊥AB,AC⊥AB,∴EK∥AC。又∵∠B=30°,
∴ AC=BC=EB=EC。又EK=EB,∴EK=AC,即AK=KE=EC=CA,∴四边形AKEC是菱形。
8.解:(1)证明:AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90o。
∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90o。
∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC。
(2)过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM。
∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴。
设CM=CE=x,∵CE:CP=2:3,∴PC=。∵AB=AD=AC=1,
∴,解得:x=,故AE=1-=。
9.解:(1)∠DEF=∠AEF。
理由:∵EF∥AB,∴∠DEF=∠EBA,∠AEF=∠EAB,
∵∠EAB=∠EBA,∴∠DEF=∠AEF;
(2)△EOA∽△AGB,
理由:∵四边形ABCD是菱形,∴AB=AD,AC⊥BD,
∴∠GAB=∠ABE+∠ADB=2∠ABE.∵∠AEO=∠ABE+∠BAE=2∠ABE,
∴∠GAB=∠AEO。∵∠AGB=∠AOE=90o,∴△EOA∽△AGB;
(3)证明:如图所示,连接DM。
∵四边形ABCD是菱形,∴由对称性可知,BM=DM,∠ADM=∠ABM.
∵AB∥CH,∴∠ABM=∠H,∴∠ADM=∠H,∵∠DMH=∠FMD,
∴△MFD∽△MDH,∴,
∴DM2=MF·MH,∴BM2=MF·MH。
10.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
B2(10,8)。
