2020届人教A版(文科数学) 形如向量AD=xAC+yAB条件的应用 单元测试
文档属性
| 名称 | 2020届人教A版(文科数学) 形如向量AD=xAC+yAB条件的应用 单元测试 |  | |
| 格式 | zip | ||
| 文件大小 | 423.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-17 09:27:35 | ||
图片预览



文档简介
2020届人教A版(文科数学) 形如向量AD=xAC+yAB条件的应用 单元测试
1、如图,在正方形中,为的中点,是以为圆心,为半径的圆弧上的任意一点,设,则的最小值为__________
答案:
2、(2018,郑州一测)已知点,,,平面区域是由所有满足的点组成的区域,若区域的面积为,则的最小值为________.
3、(2015,北京)在中,点,满足.若,则 ; .
4、(2015,新课标I)设为所在平面内一点,且,则( )
A. B.
C. D.
5、(安徽六校联考)如图,在扇形中,,为弧上且与不重合的一个动点,且,若存在最大值,则的取值范围为( )
A. B. C. D.
6、(2018,河南中原第一次联考)在直角梯形中,为边上一点,为中点,则( )
A. B. C. D.
7、如图,在直角梯形中,,动点在以点为圆心,且与直线相切的圆上或圆内移动,设,则的取值范围是( )
A. B. C. D.
8、如图,四边形是边长为1的正方形,,点为内(含边界)的动点,设,则的最大值等于__________
9、在中,,若(是的外心),则的值为___________
10、在中,边,过作于,且,则________
11、如图,是圆的直径,是圆上的点,且 若,则( )
A. B. C. D.
12、如图,将的直角三角板和的直角三角板拼在一起组成平面四边形,其中的直角三角板的斜边与的直角三角板的所对的直角边重合,若,则分别等于( )
A. B. C. D.
13、如图,在中,,过点的直线分别交射线于不同的两点,若,则的最小值为( )
A. B. C. D.
14、在中,点在线段的延长线上,且,点在线段上(与不重合),若,则的取值范围是________
15、已知在中,,点为的外心,若,则有序实数对为( )
A. B. C. D.
习题答案:
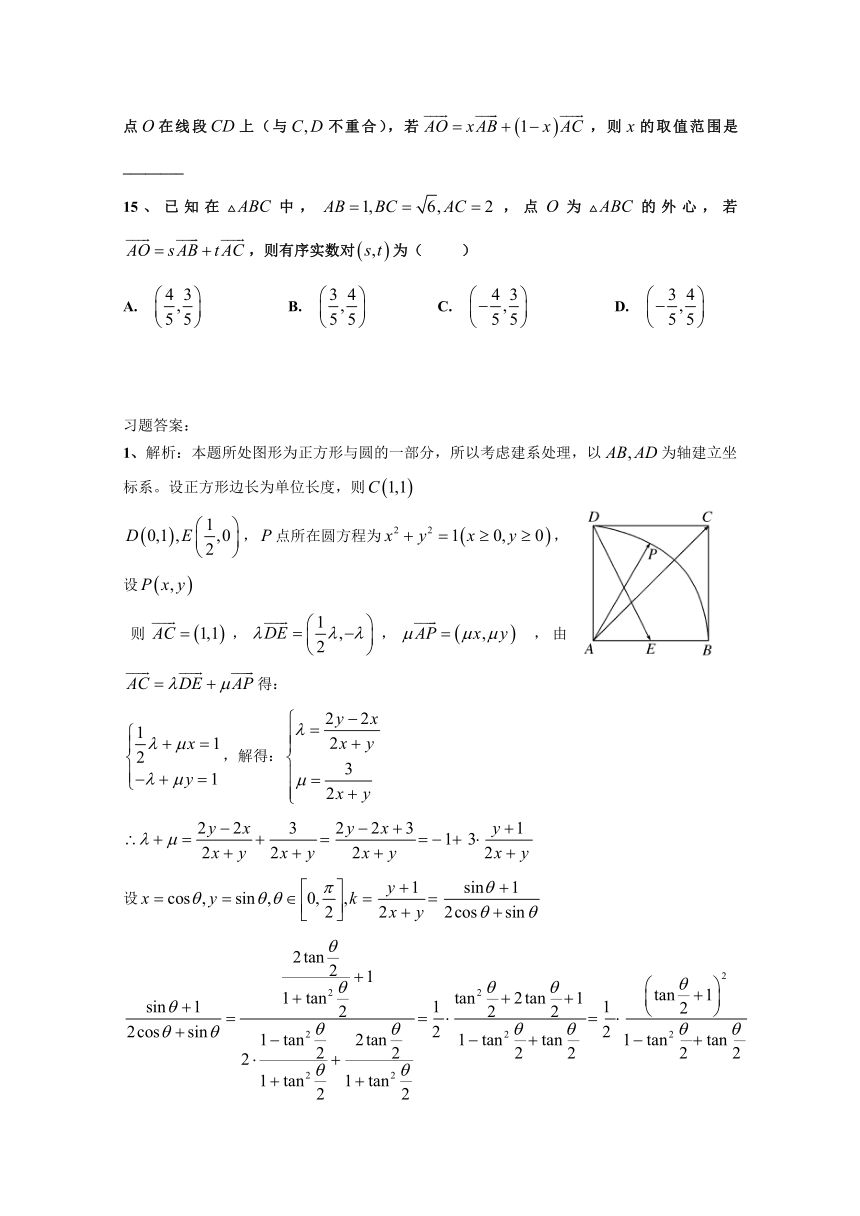
1、解析:本题所处图形为正方形与圆的一部分,所以考虑建系处理,以为轴建立坐标系。设正方形边长为单位长度,则
,点所在圆方程为,设
则,, ,由得:
,解得:
设
令,所以:
由可得:,结合分式的单调性可得当时,达到最小值,即
2、答案:
解析:设,,
∵,∴.
∴,∴,
∵∴,即
∴表示的可行域为平行四边形,如图:
由,得,由,得,
∴,
∵到直线的距离,
∴,
∴,∴,
∴,.
3、答案:
解析:,所以
4、答案:A
解析:由图可想到“爪字形图得:,解得:
5、答案:D
解析:以为轴建立坐标系,设,则,,由可得:
,若存在最大值,则存在极值点
在有零点
令,因为
,解得:
6、解析:取的中点,连结,,则,所以,
=,于是==
7、答案:C
解析:由直角梯形可知依直角建立坐标系,则,直线
圆的半径
设,由可得:
在圆内
设,则
,其中
由可知
,且
所以
8、答案:
解析:可依直角建立坐标系,则
设,则有,由图可得所在的区域为不等式组: 所求,利用线性规划可得:的最大值为,最优解在处取得
9、答案:
解析:由可得:
由是的外心可得:
,所以
10、答案:
解析:,由可得:,所以
即
另一方面,由三点共线可得:,所以解得: ,所以
11、答案:A
解析:以圆为单位圆建系,可得
由图可知,所以
,由可得:
从而
12、答案:D
解析:可如图以所在直线为轴建立坐标系,以为单位长度,则只需求出点坐标即可,由已知可得:
,联立方程可解得,所以可得:
13、答案:D
解析:连结,由“爪字型”图的模型可知,因为,代入可得:①,在中,由三点共线以及①可得:,所以,设,则,因为,所以可得的最小值在处取得,即
14、答案:
解析:设
15、答案:A
解析:
为的外心
由可得:
解得:,所以为
1、如图,在正方形中,为的中点,是以为圆心,为半径的圆弧上的任意一点,设,则的最小值为__________
答案:
2、(2018,郑州一测)已知点,,,平面区域是由所有满足的点组成的区域,若区域的面积为,则的最小值为________.
3、(2015,北京)在中,点,满足.若,则 ; .
4、(2015,新课标I)设为所在平面内一点,且,则( )
A. B.
C. D.
5、(安徽六校联考)如图,在扇形中,,为弧上且与不重合的一个动点,且,若存在最大值,则的取值范围为( )
A. B. C. D.
6、(2018,河南中原第一次联考)在直角梯形中,为边上一点,为中点,则( )
A. B. C. D.
7、如图,在直角梯形中,,动点在以点为圆心,且与直线相切的圆上或圆内移动,设,则的取值范围是( )
A. B. C. D.
8、如图,四边形是边长为1的正方形,,点为内(含边界)的动点,设,则的最大值等于__________
9、在中,,若(是的外心),则的值为___________
10、在中,边,过作于,且,则________
11、如图,是圆的直径,是圆上的点,且 若,则( )
A. B. C. D.
12、如图,将的直角三角板和的直角三角板拼在一起组成平面四边形,其中的直角三角板的斜边与的直角三角板的所对的直角边重合,若,则分别等于( )
A. B. C. D.
13、如图,在中,,过点的直线分别交射线于不同的两点,若,则的最小值为( )
A. B. C. D.
14、在中,点在线段的延长线上,且,点在线段上(与不重合),若,则的取值范围是________
15、已知在中,,点为的外心,若,则有序实数对为( )
A. B. C. D.
习题答案:
1、解析:本题所处图形为正方形与圆的一部分,所以考虑建系处理,以为轴建立坐标系。设正方形边长为单位长度,则
,点所在圆方程为,设
则,, ,由得:
,解得:
设
令,所以:
由可得:,结合分式的单调性可得当时,达到最小值,即
2、答案:
解析:设,,
∵,∴.
∴,∴,
∵∴,即
∴表示的可行域为平行四边形,如图:
由,得,由,得,
∴,
∵到直线的距离,
∴,
∴,∴,
∴,.
3、答案:
解析:,所以
4、答案:A
解析:由图可想到“爪字形图得:,解得:
5、答案:D
解析:以为轴建立坐标系,设,则,,由可得:
,若存在最大值,则存在极值点
在有零点
令,因为
,解得:
6、解析:取的中点,连结,,则,所以,
=,于是==
7、答案:C
解析:由直角梯形可知依直角建立坐标系,则,直线
圆的半径
设,由可得:
在圆内
设,则
,其中
由可知
,且
所以
8、答案:
解析:可依直角建立坐标系,则
设,则有,由图可得所在的区域为不等式组: 所求,利用线性规划可得:的最大值为,最优解在处取得
9、答案:
解析:由可得:
由是的外心可得:
,所以
10、答案:
解析:,由可得:,所以
即
另一方面,由三点共线可得:,所以解得: ,所以
11、答案:A
解析:以圆为单位圆建系,可得
由图可知,所以
,由可得:
从而
12、答案:D
解析:可如图以所在直线为轴建立坐标系,以为单位长度,则只需求出点坐标即可,由已知可得:
,联立方程可解得,所以可得:
13、答案:D
解析:连结,由“爪字型”图的模型可知,因为,代入可得:①,在中,由三点共线以及①可得:,所以,设,则,因为,所以可得的最小值在处取得,即
14、答案:
解析:设
15、答案:A
解析:
为的外心
由可得:
解得:,所以为
