正态分布 课件 (21张 ）

2.4 正态分布
会宁县第一中学
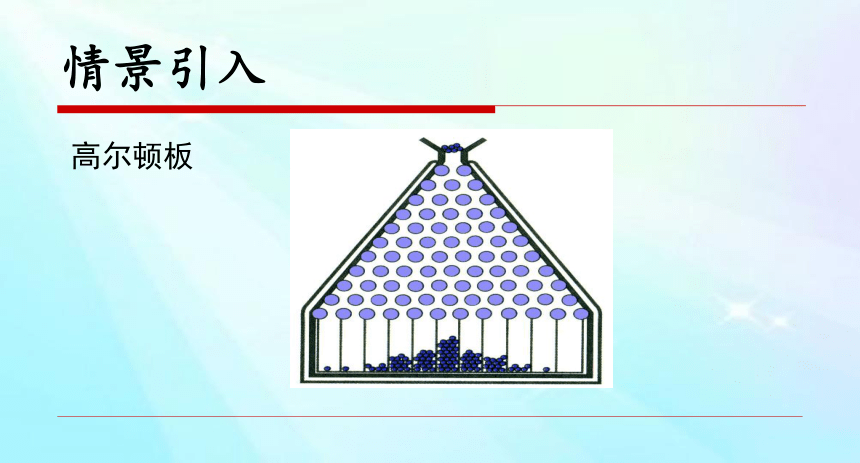
高尔顿板
情景引入
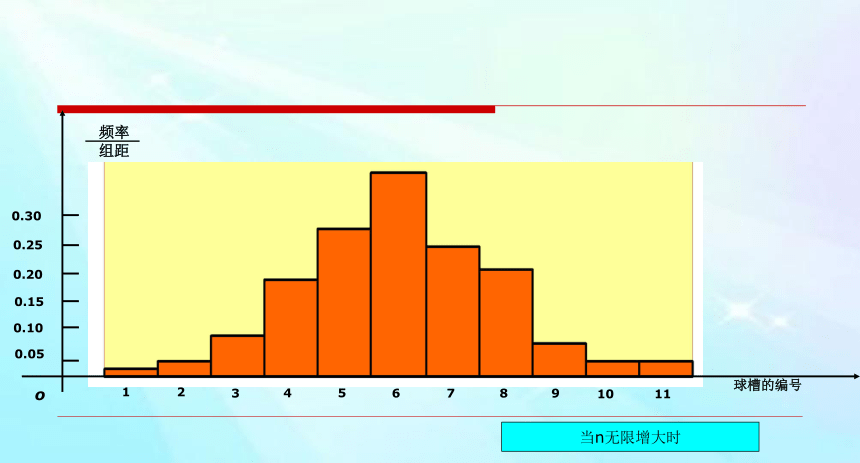
球槽的编号
o
0.05
0.15
0.10
0.20
0.25
0.30
1
2
3
4
5
6
7
8
9
10
11
当n无限增大时
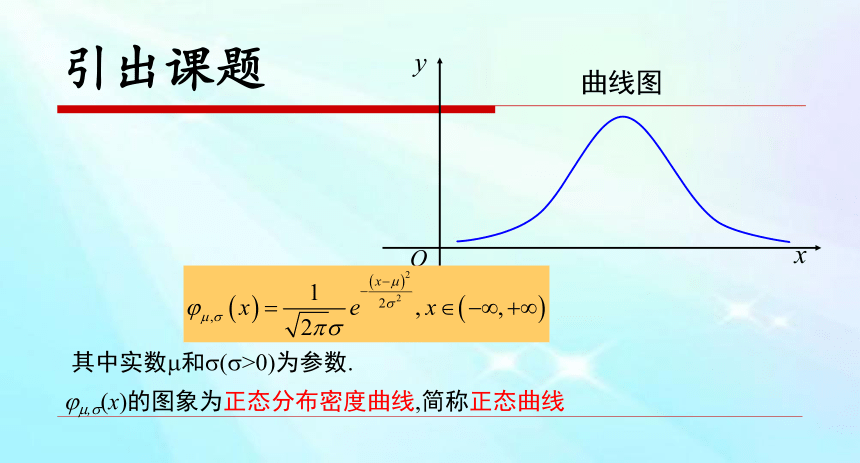
其中实数?和?(?>0)为参数.
??,?(x)的图象为正态分布密度曲线,简称正态曲线
引出课题
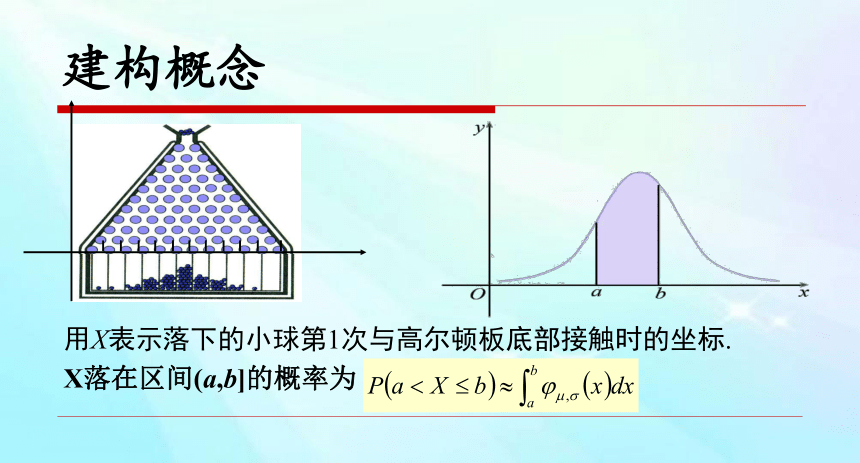
用X表示落下的小球第1次与高尔顿板底部接触时的坐标.
建构概念
X落在区间(a,b]的概率为
则称随机变量X服从正态分布
如果对于任何实数aX服从正态分布,则记
?是反映随机变量取值的平均水平的特征数，可以用样本均值去估计；
?是衡量随机变量总体波动大小的特征数，可以用样本标准差去估计.
一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布.
正态分布
如：
（1）长度测量的误差
（2）某一地区同龄人群的身高、体重、肺活量
（3）一定条件下生长的小麦的株高、穗长、单位面积的产量
（4）某一次考试的成绩
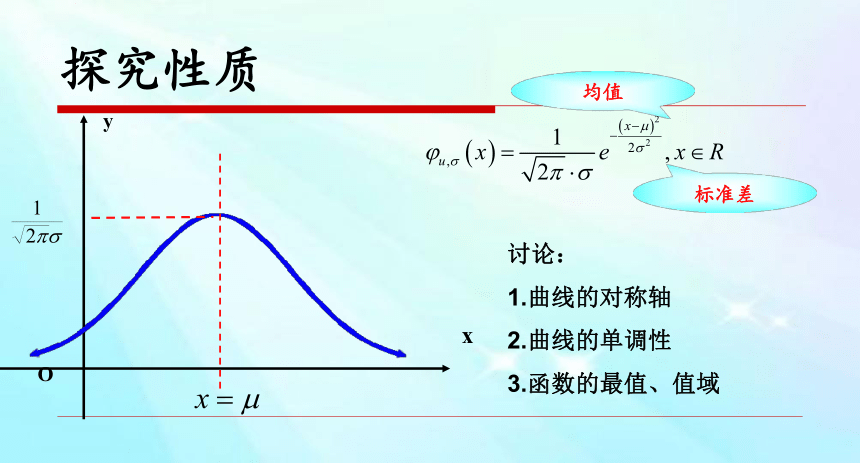
均值
标准差
探究性质
讨论：
1.曲线的对称轴
2.曲线的单调性
3.函数的最值、值域
(1) 曲线在x轴的上方,与x轴不相交；
(4) 曲线与 x 轴之间的面积为1;
(2) 曲线是单峰的，它关于直线 x=μ对称；
(3) 曲线在x=μ 处达到峰值 ；
归纳正态曲线特点
参数μ、σ对曲线的影响
σ=0.5
μ=-1
μ=0　
μ=1
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴移动
?
?=1
μ=0　
(6)当μ一定时，曲线的形状由σ确定 .
σ越大，曲线越“矮胖”，表示总体的分布越分散；
σ越小，曲线越“瘦高”，表示总体的分布越集中.
巩固知新
特殊区间的概率:
对于固定的μ和a而言，该面积随着σ的减少怎样变化？
特别有
原则
之间的值，
学以致用
例2.若X～N(5,1),求P(50.5
2.已知X服从正态分布N（1，?2）（?>0），若X在（0，1）
内取值的概率为0.4，则?在（0，2）内取值的概率为 .
0.8
练一练
作业
P75习题2.4 A组 1,2