人教版七年级数学下册第九章不等式与不等式组9.3一元一次不等式组课件(共31张)
文档属性
| 名称 | 人教版七年级数学下册第九章不等式与不等式组9.3一元一次不等式组课件(共31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-20 14:30:50 | ||
图片预览








文档简介
问题1
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端.这时爸爸的一端仍然着地.后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地,猜猜小宝的体重约是多少?
在这个问题中,如果设小宝的体重为x千克.
(1)从跷跷板的状况你可以概括出怎样的不等关系?
(2)你认为怎样求x的范围,可以尽可能地接近小宝的体重?
列不等式:
2x + x < 72
2x + x + 6 > 72
其中x同时满足以上两个不等式
一个量需要同时满足几个不等式的例子,在现实生活中还有很多.
用每分钟可抽30t的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
设用x min将污水抽完,则x同时满足不等式
30x>1200, ①
30x<1500. ②
怎样确定不等式组中的x的可取值范围呢?
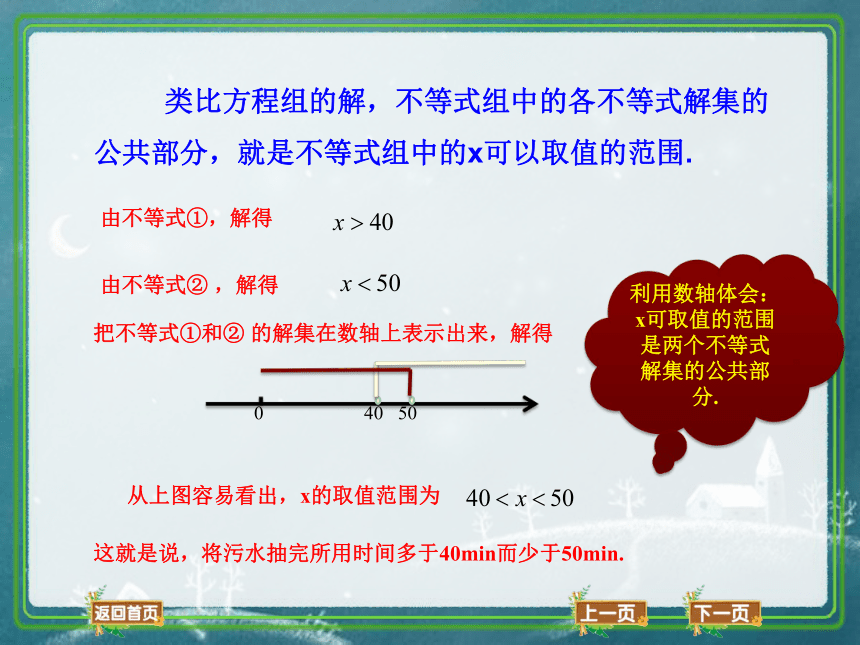
类比方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中的x可以取值的范围.
由不等式①,解得
由不等式② ,解得
把不等式①和② 的解集在数轴上表示出来,解得
从上图容易看出,x的取值范围为
这就是说,将污水抽完所用时间多于40min而少于50min.
利用数轴体会:x可取值的范围是两个不等式解集的公共部分.
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量至少是两个或者多个.
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组.
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
解不等式组就是求它的解集.
②
①
动手操作:
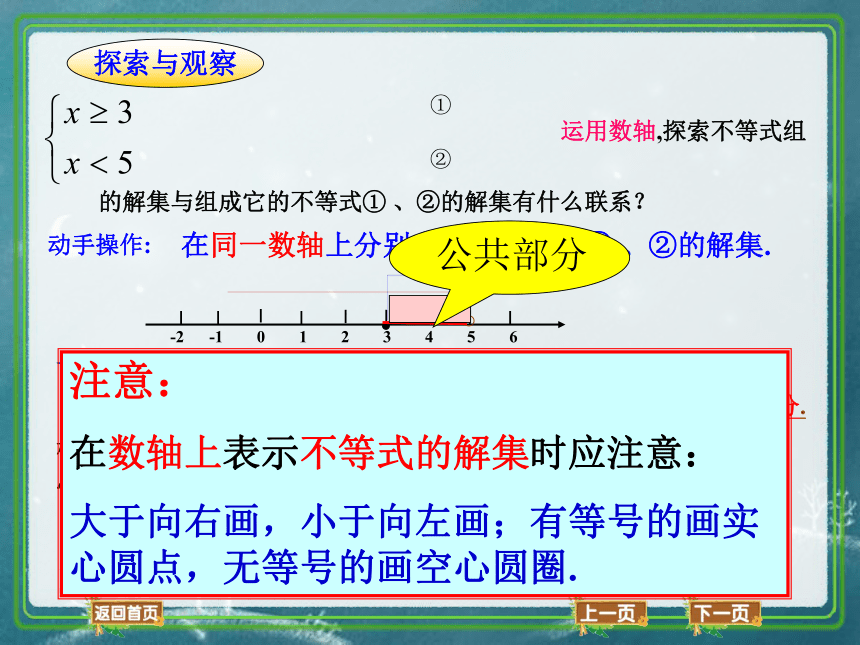
探索与观察
运用数轴,探索不等式组
的解集与组成它的不等式① 、②的解集有什么联系?
认真观察:
类似于方程组,不等式组的解集是组成它的各不等式解集的公共部分.
根据数轴你能看出不等式组的解集吗?
它与不等式组中各不等式① 、②的解集有何联系?
在同一数轴上分别表示出不等式① 、②的解集.
注意:
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
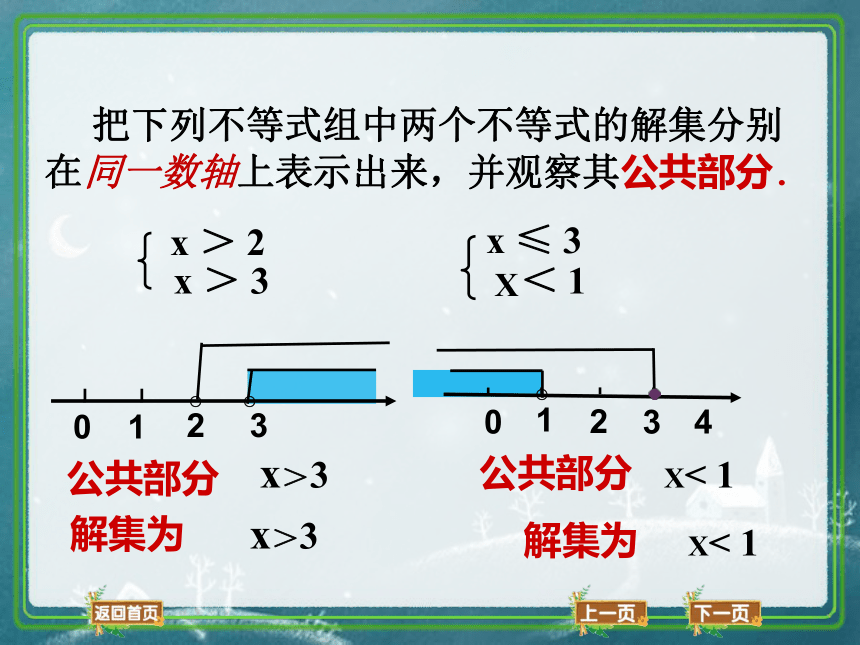
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分.
x > 2
x > 3
x ≤ 3
X
<
1
?
你会找公共部分吗
动手画一画,一起找一找.
让我们一起动手共同完成…
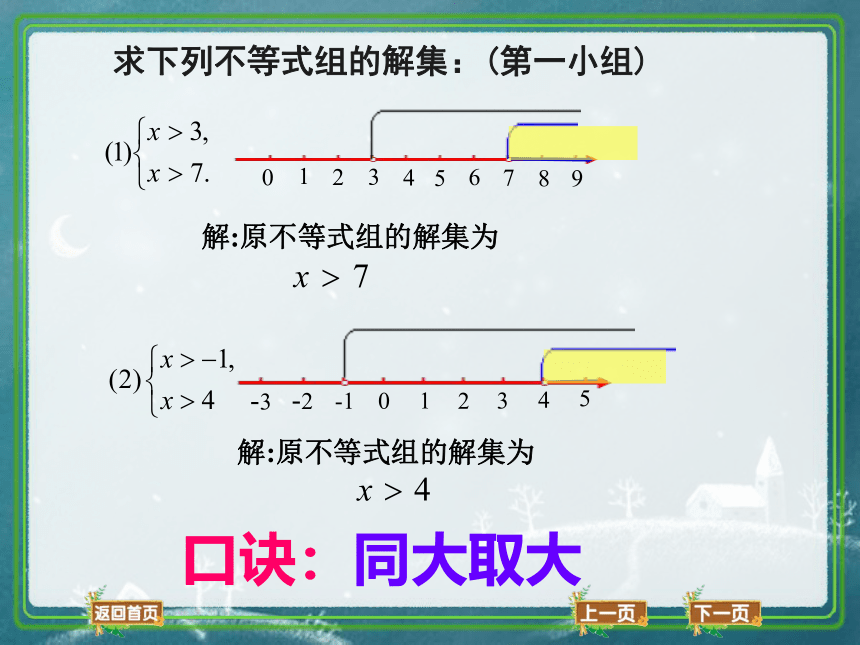
求下列不等式组的解集:(第一小组)
口诀:同大取大
求下列不等式组的解集:(第二小组)
口诀:同小取小
求下列不等式组的解集:(第三小组)
口诀:大小小大中间找
求下列不等式组的解集:(第四小组)
解:原不等式组无解.
解:原不等式组无解.
口诀:大大小小无解了
七个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们组将直接过关;否则要考验你们数学问题哦!
快乐之旅
1
2
3
4
5
7
6
1. 不等式组 的解集在数轴上表示为( )
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
x≥-5,
x<- 2
?
你会找公共部分吗
c
恭喜你,过关了!
-3
-2
-1
0
4
2
1
3
5
2.两个不等式的解集在数轴上如图所示:
则由这两个不等式组成的不等式组的解集是( )
A x<4
B x<-1
C x≤4
D x≤-1
D
?
你会找公共部分吗
恭喜你,过关了!
3.如图, 则其解集是( )
A. X ≤ 4
C. 2.5 < x ≤4
D 2.5 < X < 4
0
2.5
4
B 2.5< x
C
?
你会找公共部分吗
恭喜你,过关了!
D
?
你会找公共部分吗
恭喜你,过关了!
例1:解下列不等式组
解: 由不等式①
由不等式②,
解得:x>3
把不等式①和 ②的解集在数轴上表示出来:
②
①
所以不等式组的解集:
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集.
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
1. 由几个一元一次不等式所组成的不等式组叫做一 元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集.
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小无解了.
感受数学思想
1.与方程组的类比引入不等式组.
2.利用数轴直观地表示不等式组的解集.
类比思想
数形结合思想
随堂检测题
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端.这时爸爸的一端仍然着地.后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地,猜猜小宝的体重约是多少?
在这个问题中,如果设小宝的体重为x千克.
(1)从跷跷板的状况你可以概括出怎样的不等关系?
(2)你认为怎样求x的范围,可以尽可能地接近小宝的体重?
列不等式:
2x + x < 72
2x + x + 6 > 72
其中x同时满足以上两个不等式
一个量需要同时满足几个不等式的例子,在现实生活中还有很多.
用每分钟可抽30t的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
设用x min将污水抽完,则x同时满足不等式
30x>1200, ①
30x<1500. ②
怎样确定不等式组中的x的可取值范围呢?
类比方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中的x可以取值的范围.
由不等式①,解得
由不等式② ,解得
把不等式①和② 的解集在数轴上表示出来,解得
从上图容易看出,x的取值范围为
这就是说,将污水抽完所用时间多于40min而少于50min.
利用数轴体会:x可取值的范围是两个不等式解集的公共部分.
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量至少是两个或者多个.
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组.
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
解不等式组就是求它的解集.
②
①
动手操作:
探索与观察
运用数轴,探索不等式组
的解集与组成它的不等式① 、②的解集有什么联系?
认真观察:
类似于方程组,不等式组的解集是组成它的各不等式解集的公共部分.
根据数轴你能看出不等式组的解集吗?
它与不等式组中各不等式① 、②的解集有何联系?
在同一数轴上分别表示出不等式① 、②的解集.
注意:
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分.
x > 2
x > 3
x ≤ 3
X
<
1
?
你会找公共部分吗
动手画一画,一起找一找.
让我们一起动手共同完成…
求下列不等式组的解集:(第一小组)
口诀:同大取大
求下列不等式组的解集:(第二小组)
口诀:同小取小
求下列不等式组的解集:(第三小组)
口诀:大小小大中间找
求下列不等式组的解集:(第四小组)
解:原不等式组无解.
解:原不等式组无解.
口诀:大大小小无解了
七个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们组将直接过关;否则要考验你们数学问题哦!
快乐之旅
1
2
3
4
5
7
6
1. 不等式组 的解集在数轴上表示为( )
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
x≥-5,
x<- 2
?
你会找公共部分吗
c
恭喜你,过关了!
-3
-2
-1
0
4
2
1
3
5
2.两个不等式的解集在数轴上如图所示:
则由这两个不等式组成的不等式组的解集是( )
A x<4
B x<-1
C x≤4
D x≤-1
D
?
你会找公共部分吗
恭喜你,过关了!
3.如图, 则其解集是( )
A. X ≤ 4
C. 2.5 < x ≤4
D 2.5 < X < 4
0
2.5
4
B 2.5< x
C
?
你会找公共部分吗
恭喜你,过关了!
D
?
你会找公共部分吗
恭喜你,过关了!
例1:解下列不等式组
解: 由不等式①
由不等式②,
解得:x>3
把不等式①和 ②的解集在数轴上表示出来:
②
①
所以不等式组的解集:
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集.
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
1. 由几个一元一次不等式所组成的不等式组叫做一 元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集.
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小无解了.
感受数学思想
1.与方程组的类比引入不等式组.
2.利用数轴直观地表示不等式组的解集.
类比思想
数形结合思想
随堂检测题
