人教新课标A版选修2-3第三章 统计案例3.1回归分析的基本思想及其初步应用(18张)
文档属性
| 名称 | 人教新课标A版选修2-3第三章 统计案例3.1回归分析的基本思想及其初步应用(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 818.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-21 07:51:09 | ||
图片预览


文档简介
高二数学 选修2-3 第三章 统计案例
*
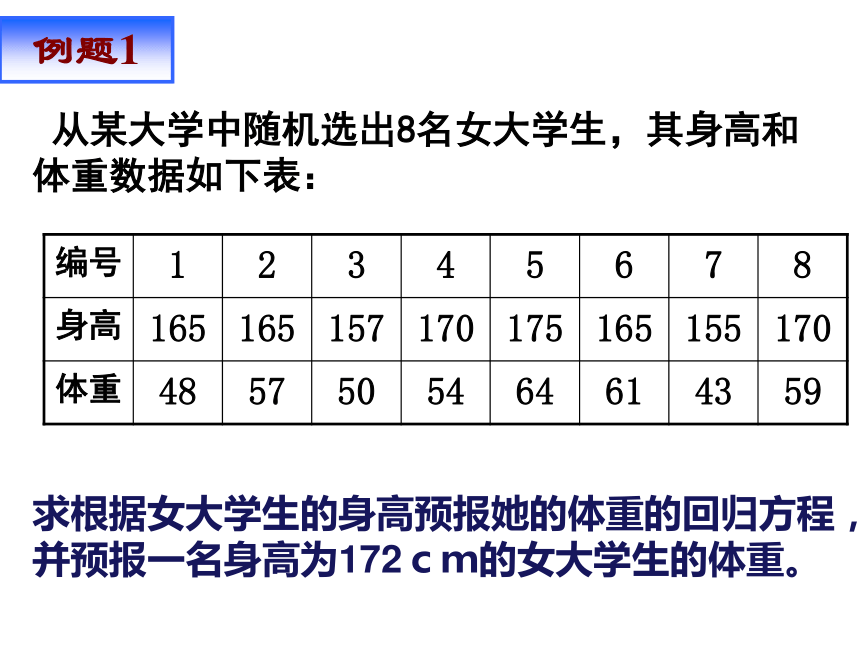
从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
例题1
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
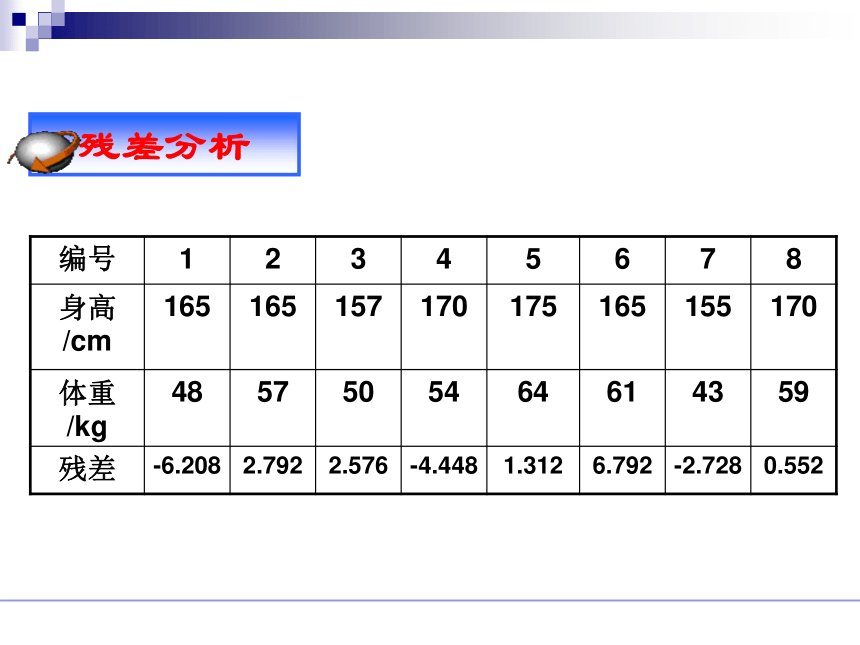
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.208 2.792 2.576 -4.448 1.312 6.792 -2.728 0.552
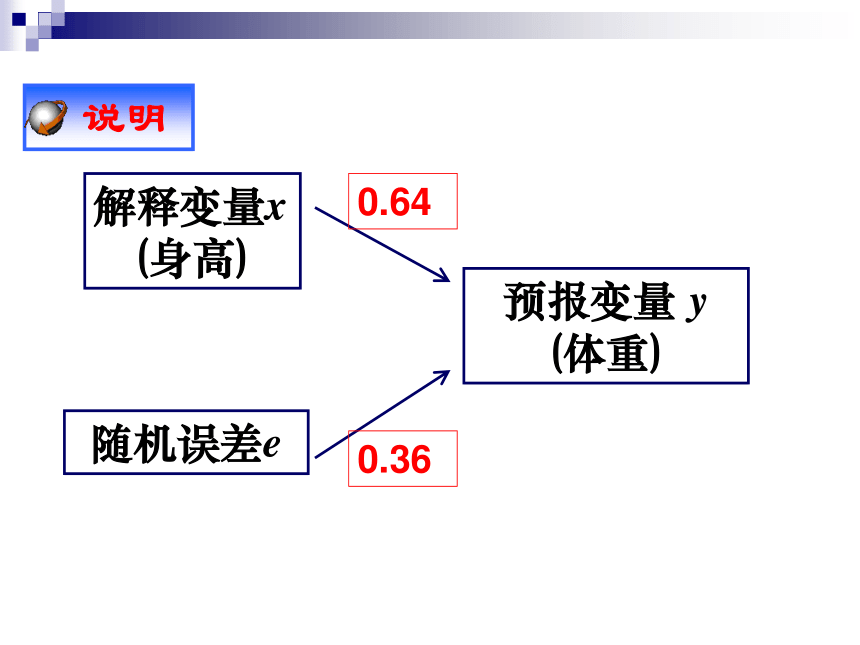
解释变量x (身高)
随机误差e
预报变量 y (体重)
0.64
0.36
用回归方程预报体重时应注意
(1)模型适用的总体;
(2)模型的时间性;
(3)样本的取值范围对模型的影响;
(4)预报结果的正确理解。
例题2
1)确定解释变量和预报变量;
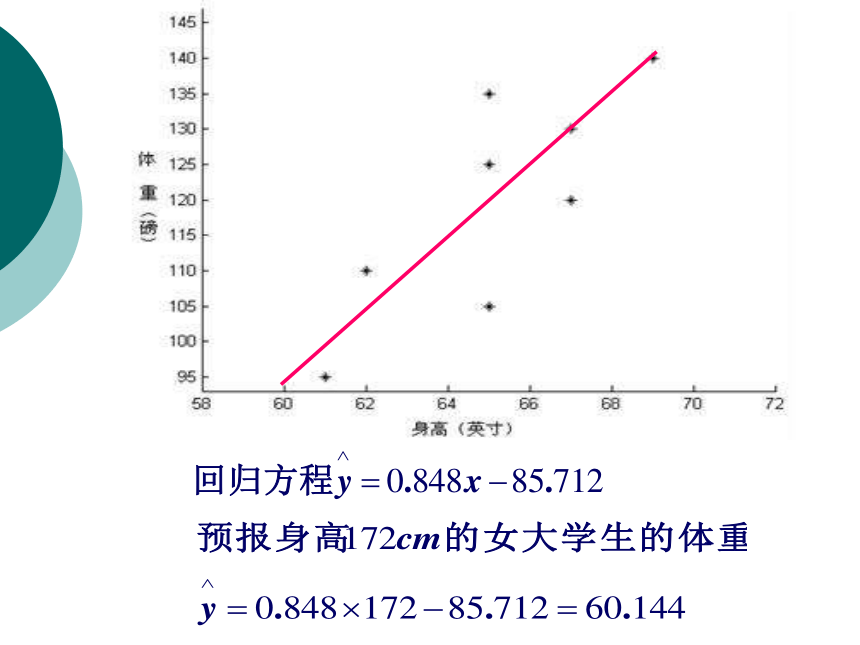
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤:
[答案] C
2.在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98
B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50
D.模型4的相关指数R2为0.25
[答案] A
4、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
(1)建立回归模型,并残差分析,计算相关指数;
(2)你认为这个模型能较好地刻画零件数和加工时间的关系吗?
编号 1 2 3 4 5 6 7 8 9 10
零件数x/个 10 20 30 40 50 60 70 80 90 100
加工时间y/分 62 68 75 81 89 95 102 108 115 122
[解] (1) 散点图,如图所示.
残差数据如下表:
编号 1 2 3 4 5
残差 0.39 -0.29 0.03 -0.65 0.67
编号 6 7 8 9 10
残差 -0.01 0.31 -0.37 -0.05 0.27
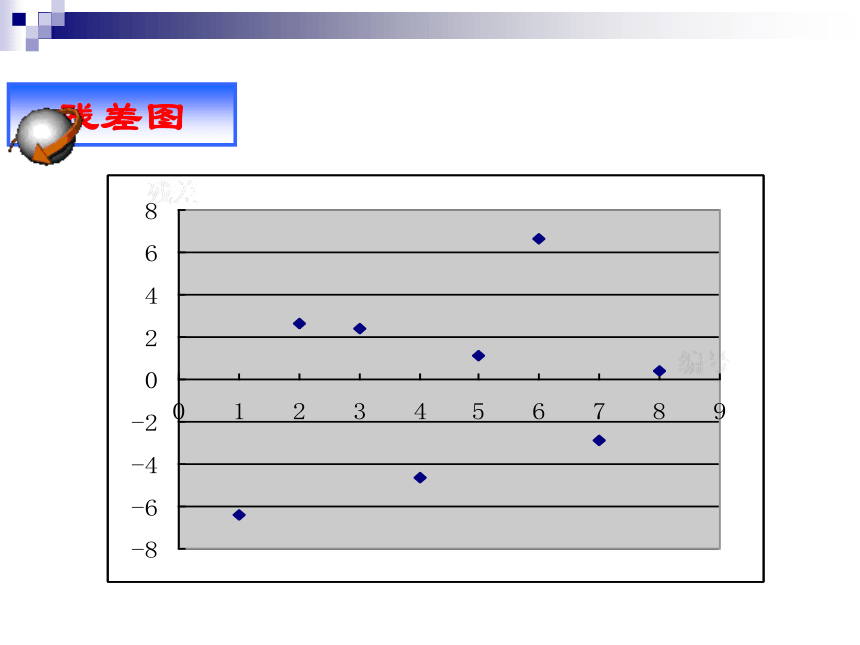
以零件数为横坐标,残差为纵坐标画出残差图如图所示.
回归分析知识结构图
*
从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
例题1
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.208 2.792 2.576 -4.448 1.312 6.792 -2.728 0.552
解释变量x (身高)
随机误差e
预报变量 y (体重)
0.64
0.36
用回归方程预报体重时应注意
(1)模型适用的总体;
(2)模型的时间性;
(3)样本的取值范围对模型的影响;
(4)预报结果的正确理解。
例题2
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤:
[答案] C
2.在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98
B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50
D.模型4的相关指数R2为0.25
[答案] A
4、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
(1)建立回归模型,并残差分析,计算相关指数;
(2)你认为这个模型能较好地刻画零件数和加工时间的关系吗?
编号 1 2 3 4 5 6 7 8 9 10
零件数x/个 10 20 30 40 50 60 70 80 90 100
加工时间y/分 62 68 75 81 89 95 102 108 115 122
[解] (1) 散点图,如图所示.
残差数据如下表:
编号 1 2 3 4 5
残差 0.39 -0.29 0.03 -0.65 0.67
编号 6 7 8 9 10
残差 -0.01 0.31 -0.37 -0.05 0.27
以零件数为横坐标,残差为纵坐标画出残差图如图所示.
回归分析知识结构图
