人教新课标A版>选修2-3 3.2独立性检验的基本思想及其初步应用(15张)
文档属性
| 名称 | 人教新课标A版>选修2-3 3.2独立性检验的基本思想及其初步应用(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-21 07:59:58 | ||
图片预览



文档简介
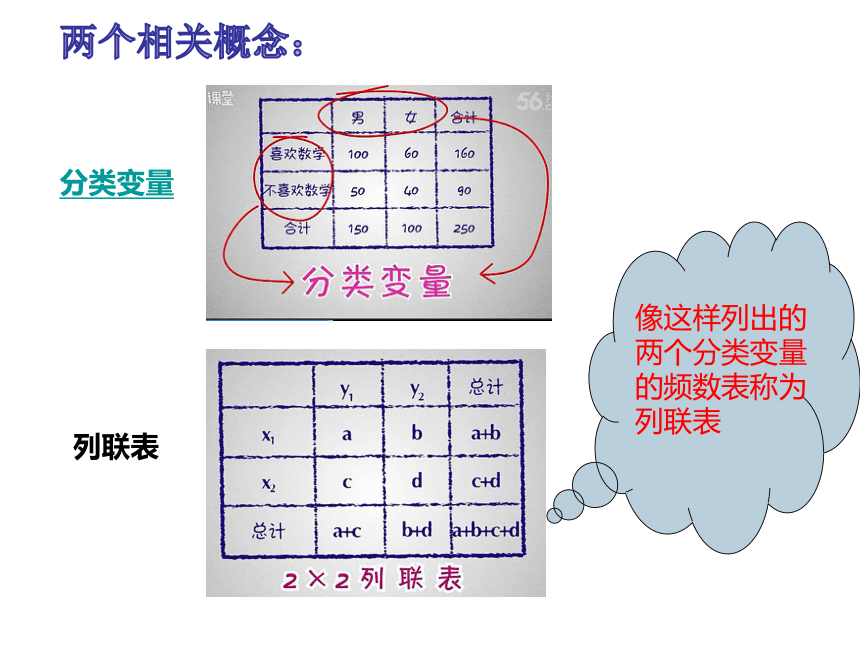
分类变量
列联表
独立性检验
本节研究的是两个分类变量的独立性检验问题。
在日常生活中,我们常常关心分类变量之间是否有关系:
例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
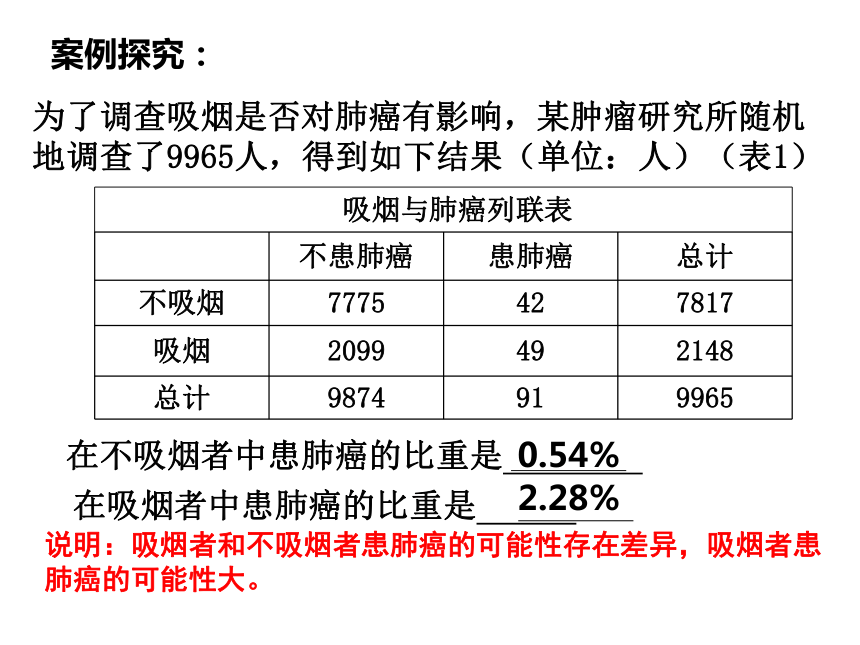
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)(表1)
说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大。
0.54%
2.28%
案例探究:
吸烟与肺癌列联表
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
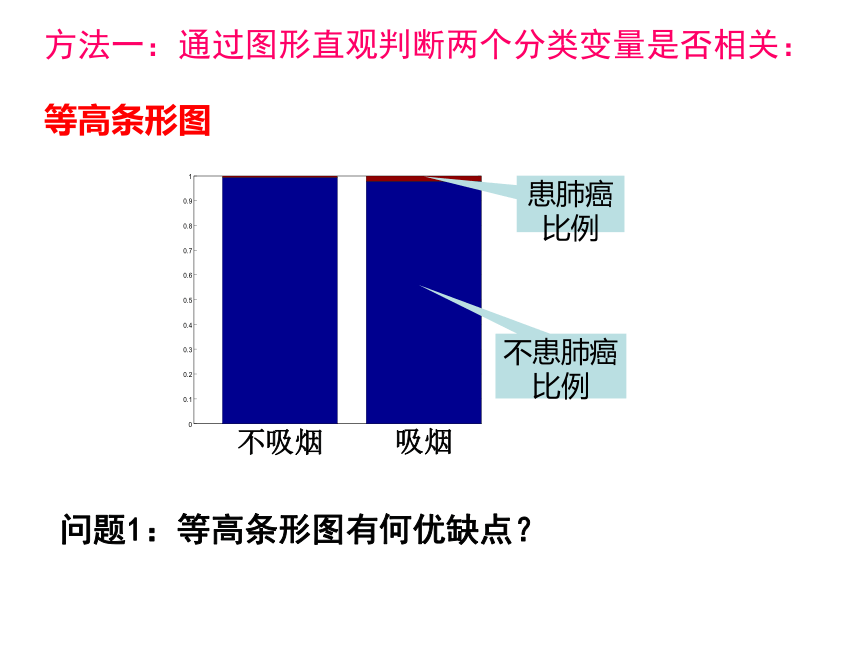
方法一:通过图形直观判断两个分类变量是否相关:
等高条形图
问题1:等高条形图有何优缺点?
上面我们通过分析数据和图形,得到的直观印象是吸烟和患肺癌有关,那么事实是否真的如此呢?这需要用统计观点来考察这个问题。
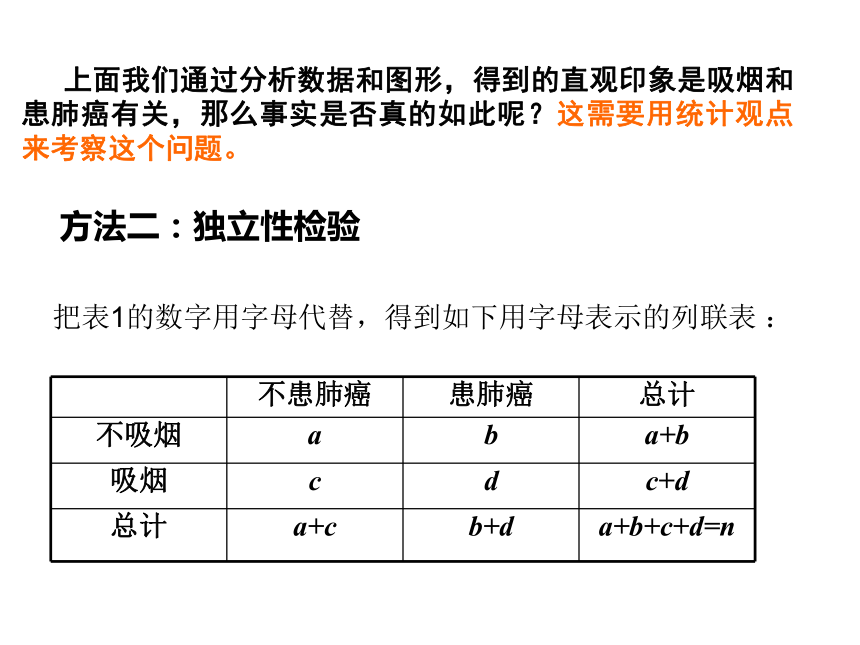
方法二:独立性检验
把表1的数字用字母代替,得到如下用字母表示的列联表 :
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d=n
现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设
H0:吸烟与患肺癌没有关系.
用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”,即假设H0等价于 P(AB)=P(A)P(B).
问题2:
因此|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
|ad-bc|越大,说明吸烟与患肺癌之间关系越强。
A表示不吸烟,B表示不患肺癌
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d=n
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量
独立性检验
统计学家们得到了如下的卡方临界值表:
在H0成立的情况下,K2的值大于6.635的概率非常小近似于0.01。
也就是说,在H0成立的情况下,对随机变量K2进行多次观测,观测值超过6.635的频率约为0.01。
问题5:
判断出错的概率为0.01。
P(K2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
回到本案例,根据表1中的数据,利用公式(1)计算得到的
观测值为 :
问题6:通过这个数据,我们能得到什么结论?
因此我们有99%以上的把握认为“患肺癌与吸烟有关”。
所以假设不成立,即:“患肺癌与吸烟有关”成立.
这个判断会犯错误,但犯错误的概率不超过0.01,
独立性检验的步骤
1.提出独立性假设H0,假设两个分类变量没有关系;
2.列出2×2列联表,并计算K2的观测值k;
3.将观测值k与临界值k0进行比较,并作出判断.
(1)当K2>2.706,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;即有_________的把握判定两个分类变量有关系;
(2) 当K2>3.841,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;有_________ 的把握判定两个分类变量有关系;
(3) 当K2>6.635,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;有_________ 的把握判定两个分类变量有关系;
90%
95%
99%
0.10
0.05
0.01
P(K2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
独立性检验的基本思想(类似反证法)
(3)根据随机变量K2的含义,可以通过评价该假设不合理的程度,由实际计算出的k的值与临界值 比较,说明假设不合理的程度,即说明“两个分类变量有关系”这一结论成立的可信度
上面这种利用随机变量K2来判断“两个分类变量有关系”的方法,称为两个分类变量的独立性检验。
类比反证法思想加深对独立性检验思想的理解:
归纳小结:
列联表
独立性检验
本节研究的是两个分类变量的独立性检验问题。
在日常生活中,我们常常关心分类变量之间是否有关系:
例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)(表1)
说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大。
0.54%
2.28%
案例探究:
吸烟与肺癌列联表
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
方法一:通过图形直观判断两个分类变量是否相关:
等高条形图
问题1:等高条形图有何优缺点?
上面我们通过分析数据和图形,得到的直观印象是吸烟和患肺癌有关,那么事实是否真的如此呢?这需要用统计观点来考察这个问题。
方法二:独立性检验
把表1的数字用字母代替,得到如下用字母表示的列联表 :
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d=n
现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设
H0:吸烟与患肺癌没有关系.
用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”,即假设H0等价于 P(AB)=P(A)P(B).
问题2:
因此|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
|ad-bc|越大,说明吸烟与患肺癌之间关系越强。
A表示不吸烟,B表示不患肺癌
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d=n
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量
独立性检验
统计学家们得到了如下的卡方临界值表:
在H0成立的情况下,K2的值大于6.635的概率非常小近似于0.01。
也就是说,在H0成立的情况下,对随机变量K2进行多次观测,观测值超过6.635的频率约为0.01。
问题5:
判断出错的概率为0.01。
P(K2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
回到本案例,根据表1中的数据,利用公式(1)计算得到的
观测值为 :
问题6:通过这个数据,我们能得到什么结论?
因此我们有99%以上的把握认为“患肺癌与吸烟有关”。
所以假设不成立,即:“患肺癌与吸烟有关”成立.
这个判断会犯错误,但犯错误的概率不超过0.01,
独立性检验的步骤
1.提出独立性假设H0,假设两个分类变量没有关系;
2.列出2×2列联表,并计算K2的观测值k;
3.将观测值k与临界值k0进行比较,并作出判断.
(1)当K2>2.706,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;即有_________的把握判定两个分类变量有关系;
(2) 当K2>3.841,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;有_________ 的把握判定两个分类变量有关系;
(3) 当K2>6.635,在犯错误的概率不超过_____的前提下认为两个分类变量有关系;有_________ 的把握判定两个分类变量有关系;
90%
95%
99%
0.10
0.05
0.01
P(K2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
独立性检验的基本思想(类似反证法)
(3)根据随机变量K2的含义,可以通过评价该假设不合理的程度,由实际计算出的k的值与临界值 比较,说明假设不合理的程度,即说明“两个分类变量有关系”这一结论成立的可信度
上面这种利用随机变量K2来判断“两个分类变量有关系”的方法,称为两个分类变量的独立性检验。
类比反证法思想加深对独立性检验思想的理解:
归纳小结:
