2019年高考靠前保温---平抛、圆周运动、 天体知识总结 42张PPT
文档属性
| 名称 | 2019年高考靠前保温---平抛、圆周运动、 天体知识总结 42张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 977.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-05-20 18:33:23 | ||
图片预览






文档简介
2019年高考保温---平抛、圆周运动、 天体
知识总结
平抛运动
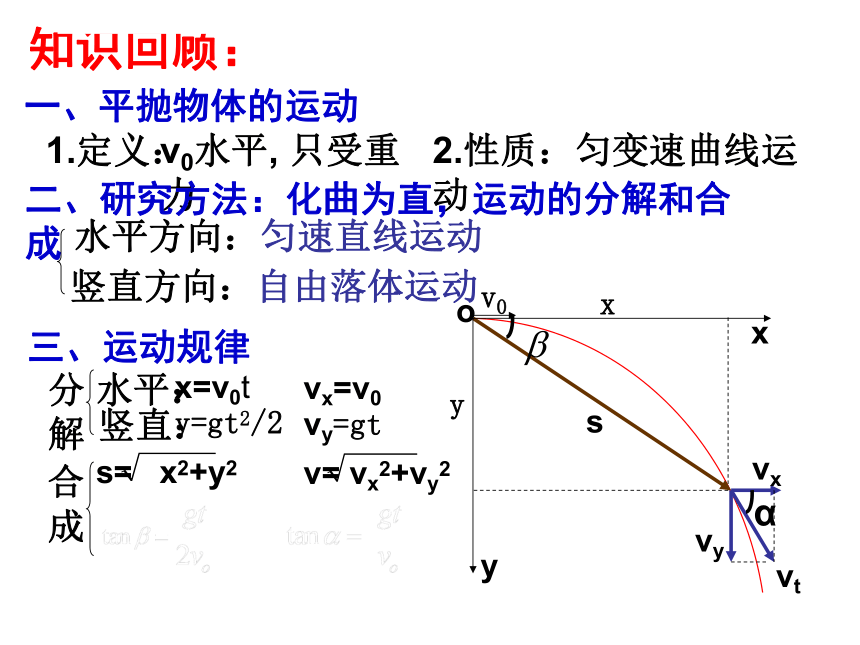
知识回顾:
一、平抛物体的运动
1.定义:
v0水平, 只受重力
水平方向:匀速直线运动
2.性质:匀变速曲线运动
竖直方向:自由落体运动
三、运动规律
x=v0t
vx=v0
y=gt2/2
vy=gt
二、研究方法:化曲为直,运动的分解和合成
水平:
竖直:
分解
合成
s= x2+y2
v= vx2+vy2
vx
vy
s
x
y
o
vt
α
x
y
v0
1、轨迹为抛物线
2、落地时间t= 2h/g,只由高度决定
3、水平射程x=v0t=v0 2h/g
v0
4、
即vt反向延长线与x轴交点是位移x的中点
四、推论
vx
vy
s
x
y
o
vt
α
x
y
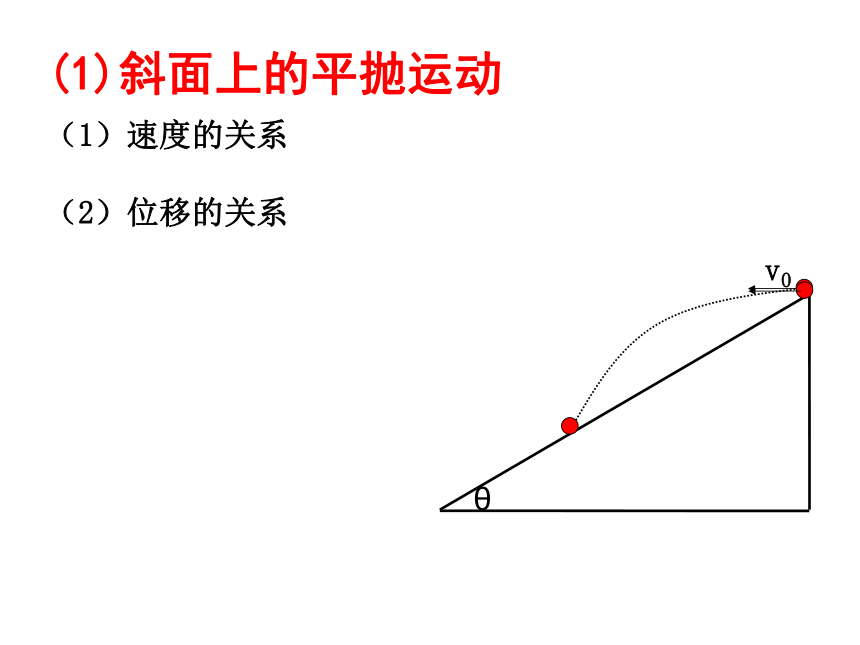
(1)速度的关系
(2)位移的关系
(1)斜面上的平抛运动
θ
v0
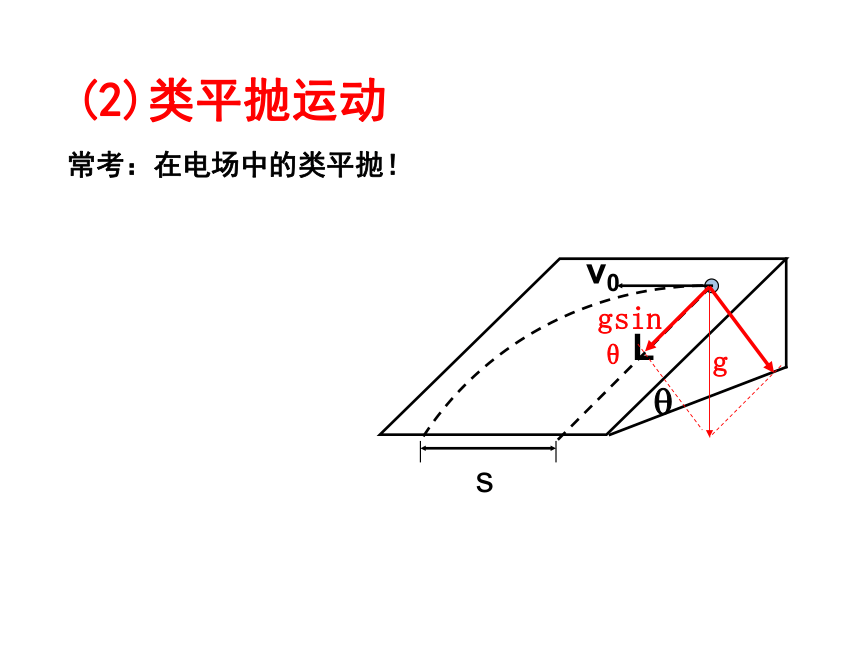
常考:在电场中的类平抛!
s
?
v0
L
(2)类平抛运动
g
gsinθ
圆周运动
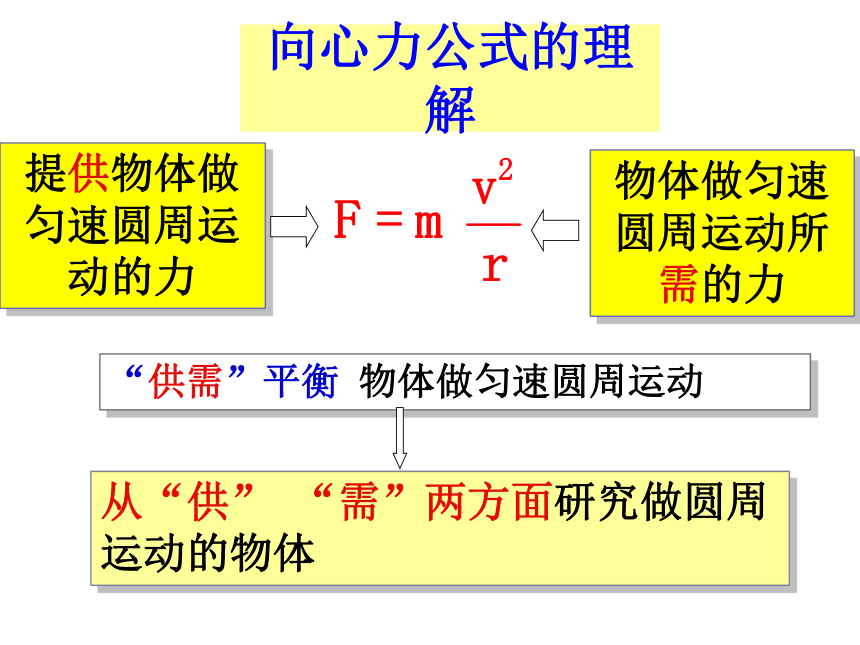
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
从“供” “需”两方面研究做圆周运动的物体
O
θ
O'
FT
mg
F合
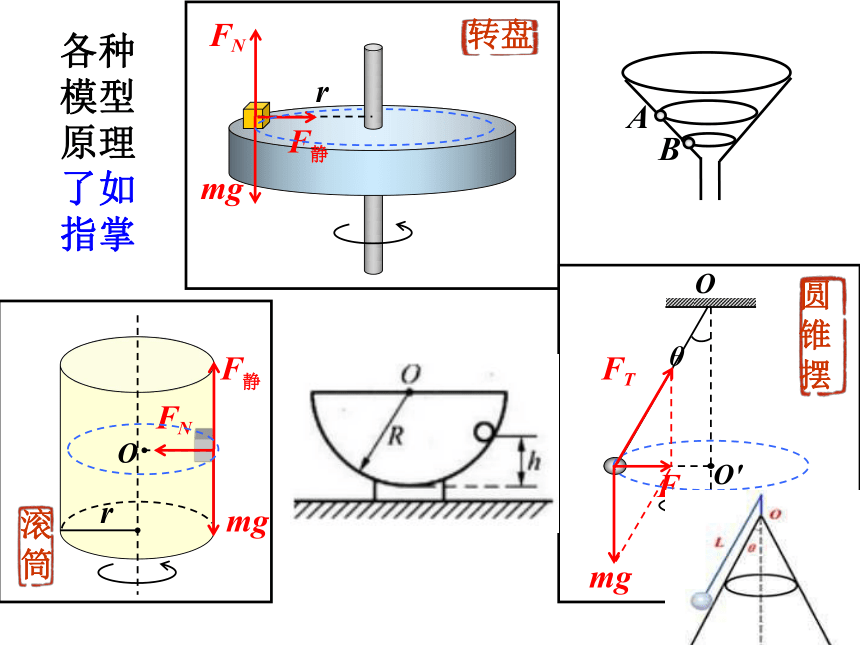
圆锥摆
mg
FN
r
F静
转盘
r
mg
F静
O
FN
滚筒
B
A
各种模型原理 了如指掌
几种常见生活物理模型
(1)汽车拐弯(水平面内圆周运动)
G
N
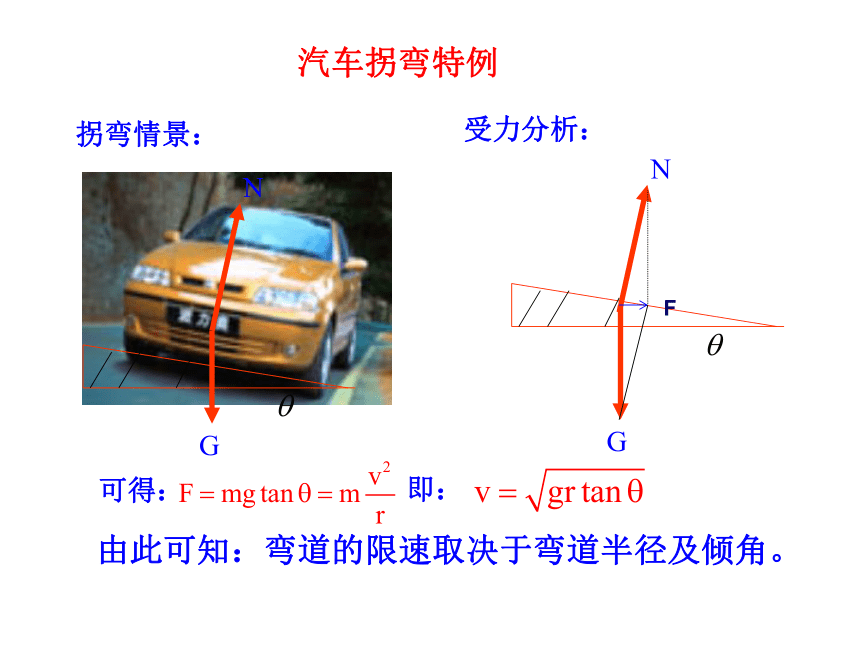
汽车拐弯特例
N
G
F
拐弯情景:
受力分析:
可得:
即:
由此可知:弯道的限速取决于弯道半径及倾角。
(2)、火车转弯(水平面内圆周运动)
N
G
向右转
(1)火车转弯处内外轨无高度差
外轨
内轨
思考讨论:
如果火车转弯时的速度超过了规定速度,那么哪一道铁轨会受到车轮轮缘挤压?
如果火车转弯时的速度小于规定速度,那么哪一道铁轨会受到车轮轮缘挤压?
当v=v0时:
当v>v0时:
当v轮缘不受侧向压力
轮缘受到外轨向内的挤压力
轮缘受到内轨向外的挤压力
F弹
F弹
因此为了保护轮缘和行驶安全,过弯道有速度限制!
2、汽车过凹桥时,在最低点时,车对凹桥的压力怎样?
v
FN
FN>G,即汽车对桥的压力大于其所受重力,处于超重状态,容易引发爆胎。
1、过凹形桥
1、汽车静止在桥上与通过桥时的状态是否相同?
G
(3)过桥(竖直面内圆周运动)
3、汽车过凸桥时,在最高点时,车对凸桥的压力又怎样?
v
G
FN
FN1、过凸形桥
若汽车的运动速度变大,压力如何变化?
会出现“飞车”现象很危险
若
是压力为零。
若
类似模型
(1)过山车 (2)水流星
水流星过最高点情况(没有支承物的物体在竖直面内做圆周运动):
(4)、绳(外轨)的模型
mg
T
解:
在最高点: T+ mg = mV2/R
解得: T = mV2/R- mg
依据此公式,你能找出T与V存在哪些关系?
1).小球对绳的拉力随速度的增大而增大;做什么运动?
2). 当 时,T=0, 小球恰过最高点;
当V> 时,T>0;
当V < 时,小球不能到达顶点.
(5).杆(有内外轨)的模型
问题: 质量为m的小球,套在长为L轻杆上在竖直平面内转动,在最高点, 试讨论
(1)速度为何值时,杆对小球无作用力?
(2)小球的速度在什么范围内,杆对小球有支持力?
(3) 在什么范围内,杆对小球有向下的拉力?
解:
(2).杆对小球有支持力N,
mg -N = mV2/R 所以 N = mg - mV2/R
根据题意, N>0,
(1). 当 时,N=0, 杆对小球无作用力.
代入上式, V<
(3).杆对小球有拉力T,
mg +N = mV2/R 所以 N = mV2/R - mg
根据题意, T>0,代入上式, V>
T
mg
N
mg
(6)圆管模型
N
mg
凸桥(外轨)
轻绳(内轨)
轻杆(圆管)
最高点受力特点
产生背离圆心的力(支持力)
产生指向圆心的力(拉力)
既可产生背离指向圆心的力也可产生指向圆心的力(支持力或拉力)
最高点特征方程
mg- N = mV2/R
Mg+T = mV2/R
Mg+T = mV2/R
产生支持力:
mg- N = mV2/R
产生拉力:
做完整圆运动的条件
竖直平面内圆周运动几种模型比较
过山车、飞机在竖直平面翻筋斗、水流星与绳模型类似
天体运动
物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
万有引力扮演的角色是什么?如何表示?
回顾所学内容
(1)天体或者人造天体(卫星)沿着圆轨道运动时,万有引力充当向心力。
(提供)
(需要)
(2)地球表面上的物体:
由于地球自转,静止在地球上的物体也跟着绕地轴作圆周运动,这个作圆周运动的向心力就由万有引力的一个分力来提供。因此,在地球表面上的物体所受的万有引力可以分解成物体所受的重力和随地球自转做圆周运动的向心力。
F
G
F向
F万
G
F万
G
F向
r
null
null
注意:重力只是物体所受万有引力的一个分力,但是由于另一个分力F向特别小,所以一般近似认为地球表面(附近)上的物体,所受重力等于万有引力。
黄金代换式
(1)重力加速度的计算方法:
g=
GM
R2
1。将物体放在地面:
重力 = 万有引力
2。将物体变成卫星:
万有引力提供向心力
(2)测量天体质量
当r=R时
(3)天体密度的计算
M
V
r
=
卫星在地面附近轨道绕地球做匀速圆周运动的线速度:
可得:
(4)第一宇宙速度
根据万有引力和重力关系,在近地有:
R
O
F F
=
引
向
(5)知一求四
人造卫星的线速度、角速度、周期、向心加速度与半径的关系
(6)两种特殊卫星---近地卫星
R
O
1.近地卫星:其轨道半径即地球半径R
可得:
近地卫星的线速度与第一宇宙速度一样大!
你能计算出近地卫星的周期吗?
已知:地球半径R=6400km
(6)两种特殊卫星---- 同步卫星
可得:
你能求出同步卫星的轨道半径 r 吗?
已知:地球半径R=6400km
2.同步卫星:
地面上的人看此卫星,该卫星
是不动的。
1)必须位于赤道的正上方
2)圆周运动的周期与地球自转
周期相等,为24h;角速度等
于地球自转的角速度
同步卫星离地面高度:
8.卫星的变轨
观看:嫦娥一号的发射过程模拟
发射同步卫星过程模拟
同步轨道
近地轨道
过渡轨道
加速?
减速?
加速?
减速?
加速
加速
要实现卫星从低轨道变轨到高轨道,应在变轨处对卫星加速,从而实现卫星的“离心运动”,达到变轨目的。
r
R
Q
P
(7).卫星的变轨
v1
1
F1
2
v2
从圆轨道1变轨到椭圆轨道2,在P点
圆轨道1:
椭圆轨道2:
加速!!
3
从椭圆轨道2变轨到圆轨道3,在Q点
F2
圆轨道3:
椭圆轨道2:
加速!!
v4
v3
在越高的轨道,卫星系统具有的机械能越大!
卫星变轨——同步卫星为例子
A
B
轨道1
轨道2
过渡轨道
同步卫星轨道
近地轨道
(8).“双星”问题
F万
F万
L
r1
r2
m2
m1
双星圆周运动的角速度相同,设为ω
(9).卫星的相遇问题
知识总结
平抛运动
知识回顾:
一、平抛物体的运动
1.定义:
v0水平, 只受重力
水平方向:匀速直线运动
2.性质:匀变速曲线运动
竖直方向:自由落体运动
三、运动规律
x=v0t
vx=v0
y=gt2/2
vy=gt
二、研究方法:化曲为直,运动的分解和合成
水平:
竖直:
分解
合成
s= x2+y2
v= vx2+vy2
vx
vy
s
x
y
o
vt
α
x
y
v0
1、轨迹为抛物线
2、落地时间t= 2h/g,只由高度决定
3、水平射程x=v0t=v0 2h/g
v0
4、
即vt反向延长线与x轴交点是位移x的中点
四、推论
vx
vy
s
x
y
o
vt
α
x
y
(1)速度的关系
(2)位移的关系
(1)斜面上的平抛运动
θ
v0
常考:在电场中的类平抛!
s
?
v0
L
(2)类平抛运动
g
gsinθ
圆周运动
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
从“供” “需”两方面研究做圆周运动的物体
O
θ
O'
FT
mg
F合
圆锥摆
mg
FN
r
F静
转盘
r
mg
F静
O
FN
滚筒
B
A
各种模型原理 了如指掌
几种常见生活物理模型
(1)汽车拐弯(水平面内圆周运动)
G
N
汽车拐弯特例
N
G
F
拐弯情景:
受力分析:
可得:
即:
由此可知:弯道的限速取决于弯道半径及倾角。
(2)、火车转弯(水平面内圆周运动)
N
G
向右转
(1)火车转弯处内外轨无高度差
外轨
内轨
思考讨论:
如果火车转弯时的速度超过了规定速度,那么哪一道铁轨会受到车轮轮缘挤压?
如果火车转弯时的速度小于规定速度,那么哪一道铁轨会受到车轮轮缘挤压?
当v=v0时:
当v>v0时:
当v
轮缘受到外轨向内的挤压力
轮缘受到内轨向外的挤压力
F弹
F弹
因此为了保护轮缘和行驶安全,过弯道有速度限制!
2、汽车过凹桥时,在最低点时,车对凹桥的压力怎样?
v
FN
FN>G,即汽车对桥的压力大于其所受重力,处于超重状态,容易引发爆胎。
1、过凹形桥
1、汽车静止在桥上与通过桥时的状态是否相同?
G
(3)过桥(竖直面内圆周运动)
3、汽车过凸桥时,在最高点时,车对凸桥的压力又怎样?
v
G
FN
FN
若汽车的运动速度变大,压力如何变化?
会出现“飞车”现象很危险
若
是压力为零。
若
类似模型
(1)过山车 (2)水流星
水流星过最高点情况(没有支承物的物体在竖直面内做圆周运动):
(4)、绳(外轨)的模型
mg
T
解:
在最高点: T+ mg = mV2/R
解得: T = mV2/R- mg
依据此公式,你能找出T与V存在哪些关系?
1).小球对绳的拉力随速度的增大而增大;做什么运动?
2). 当 时,T=0, 小球恰过最高点;
当V> 时,T>0;
当V < 时,小球不能到达顶点.
(5).杆(有内外轨)的模型
问题: 质量为m的小球,套在长为L轻杆上在竖直平面内转动,在最高点, 试讨论
(1)速度为何值时,杆对小球无作用力?
(2)小球的速度在什么范围内,杆对小球有支持力?
(3) 在什么范围内,杆对小球有向下的拉力?
解:
(2).杆对小球有支持力N,
mg -N = mV2/R 所以 N = mg - mV2/R
根据题意, N>0,
(1). 当 时,N=0, 杆对小球无作用力.
代入上式, V<
(3).杆对小球有拉力T,
mg +N = mV2/R 所以 N = mV2/R - mg
根据题意, T>0,代入上式, V>
T
mg
N
mg
(6)圆管模型
N
mg
凸桥(外轨)
轻绳(内轨)
轻杆(圆管)
最高点受力特点
产生背离圆心的力(支持力)
产生指向圆心的力(拉力)
既可产生背离指向圆心的力也可产生指向圆心的力(支持力或拉力)
最高点特征方程
mg- N = mV2/R
Mg+T = mV2/R
Mg+T = mV2/R
产生支持力:
mg- N = mV2/R
产生拉力:
做完整圆运动的条件
竖直平面内圆周运动几种模型比较
过山车、飞机在竖直平面翻筋斗、水流星与绳模型类似
天体运动
物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
万有引力扮演的角色是什么?如何表示?
回顾所学内容
(1)天体或者人造天体(卫星)沿着圆轨道运动时,万有引力充当向心力。
(提供)
(需要)
(2)地球表面上的物体:
由于地球自转,静止在地球上的物体也跟着绕地轴作圆周运动,这个作圆周运动的向心力就由万有引力的一个分力来提供。因此,在地球表面上的物体所受的万有引力可以分解成物体所受的重力和随地球自转做圆周运动的向心力。
F
G
F向
F万
G
F万
G
F向
r
null
null
注意:重力只是物体所受万有引力的一个分力,但是由于另一个分力F向特别小,所以一般近似认为地球表面(附近)上的物体,所受重力等于万有引力。
黄金代换式
(1)重力加速度的计算方法:
g=
GM
R2
1。将物体放在地面:
重力 = 万有引力
2。将物体变成卫星:
万有引力提供向心力
(2)测量天体质量
当r=R时
(3)天体密度的计算
M
V
r
=
卫星在地面附近轨道绕地球做匀速圆周运动的线速度:
可得:
(4)第一宇宙速度
根据万有引力和重力关系,在近地有:
R
O
F F
=
引
向
(5)知一求四
人造卫星的线速度、角速度、周期、向心加速度与半径的关系
(6)两种特殊卫星---近地卫星
R
O
1.近地卫星:其轨道半径即地球半径R
可得:
近地卫星的线速度与第一宇宙速度一样大!
你能计算出近地卫星的周期吗?
已知:地球半径R=6400km
(6)两种特殊卫星---- 同步卫星
可得:
你能求出同步卫星的轨道半径 r 吗?
已知:地球半径R=6400km
2.同步卫星:
地面上的人看此卫星,该卫星
是不动的。
1)必须位于赤道的正上方
2)圆周运动的周期与地球自转
周期相等,为24h;角速度等
于地球自转的角速度
同步卫星离地面高度:
8.卫星的变轨
观看:嫦娥一号的发射过程模拟
发射同步卫星过程模拟
同步轨道
近地轨道
过渡轨道
加速?
减速?
加速?
减速?
加速
加速
要实现卫星从低轨道变轨到高轨道,应在变轨处对卫星加速,从而实现卫星的“离心运动”,达到变轨目的。
r
R
Q
P
(7).卫星的变轨
v1
1
F1
2
v2
从圆轨道1变轨到椭圆轨道2,在P点
圆轨道1:
椭圆轨道2:
加速!!
3
从椭圆轨道2变轨到圆轨道3,在Q点
F2
圆轨道3:
椭圆轨道2:
加速!!
v4
v3
在越高的轨道,卫星系统具有的机械能越大!
卫星变轨——同步卫星为例子
A
B
轨道1
轨道2
过渡轨道
同步卫星轨道
近地轨道
(8).“双星”问题
F万
F万
L
r1
r2
m2
m1
双星圆周运动的角速度相同,设为ω
(9).卫星的相遇问题
同课章节目录
