2019年高考物理备考:动量与能量综合问题归类分析 70张PPT
文档属性
| 名称 | 2019年高考物理备考:动量与能量综合问题归类分析 70张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 891.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-05-20 00:00:00 | ||
图片预览








文档简介
2019年高考物理备考:
动量与能量综合问题
归类分析
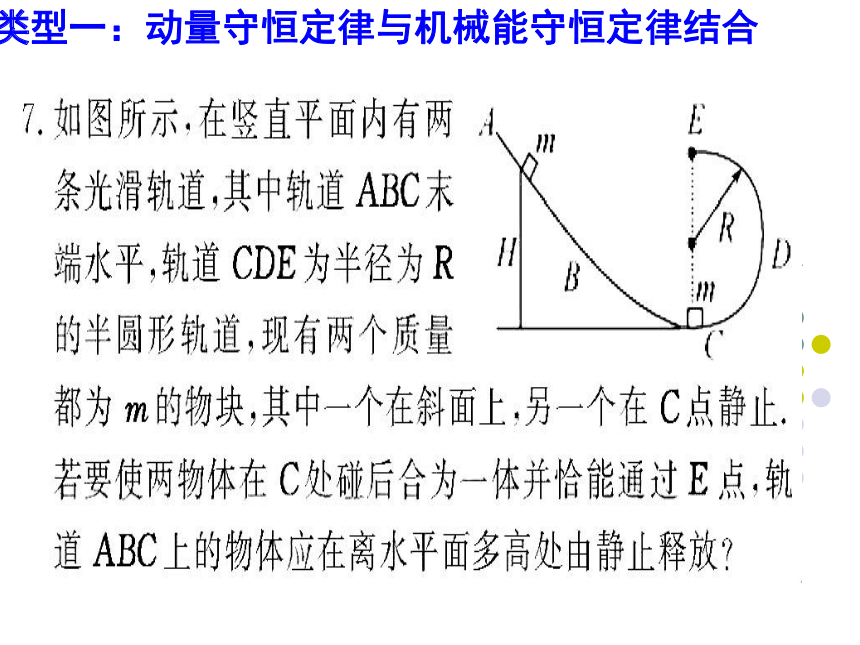
类型一:动量守恒定律与机械能守恒定律结合
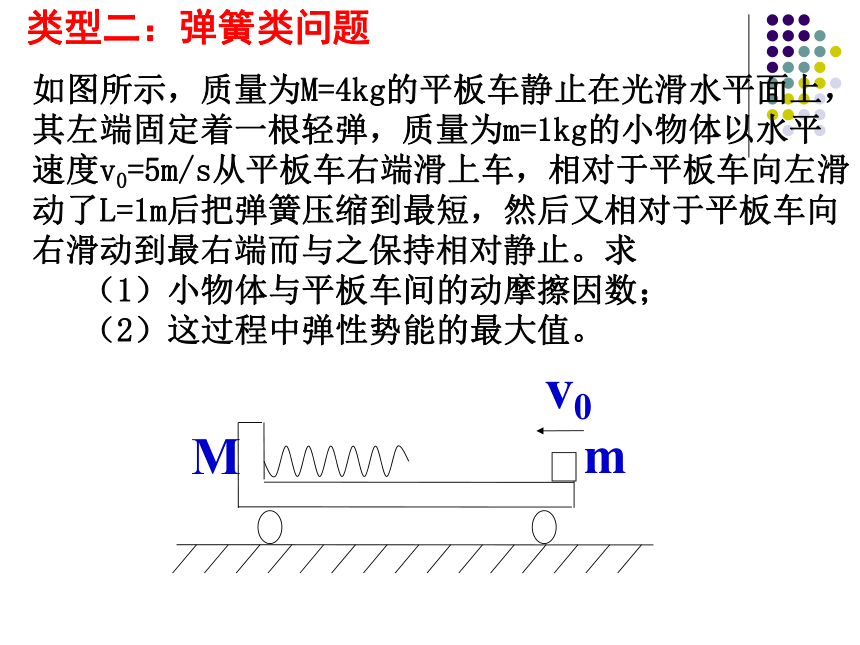
如图所示,质量为M=4kg的平板车静止在光滑水平面上,其左端固定着一根轻弹,质量为m=1kg的小物体以水平速度v0=5m/s从平板车右端滑上车,相对于平板车向左滑动了L=1m后把弹簧压缩到最短,然后又相对于平板车向右滑动到最右端而与之保持相对静止。求
(1)小物体与平板车间的动摩擦因数;
(2)这过程中弹性势能的最大值。
M
m
v0
类型二:弹簧类问题
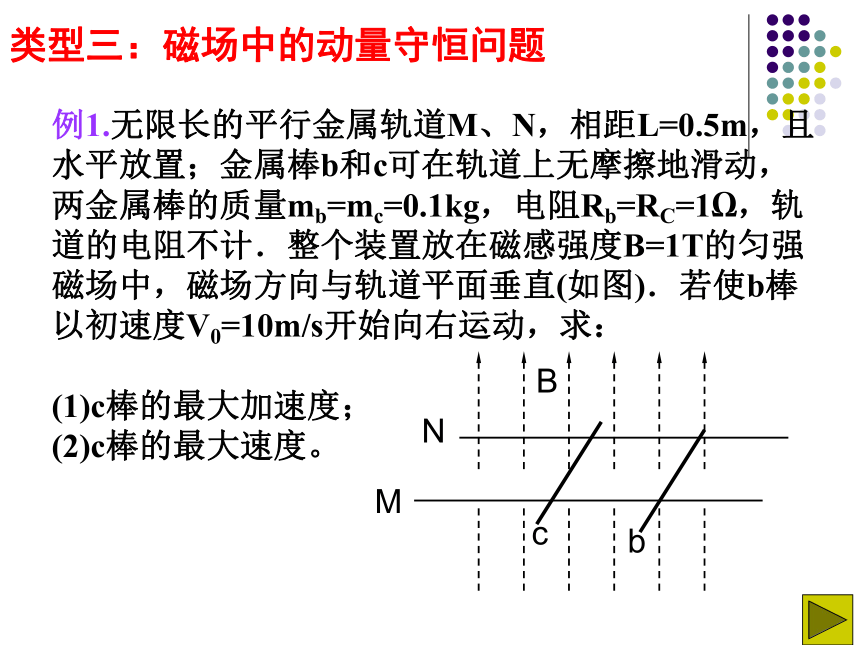
例1.无限长的平行金属轨道M、N,相距L=0.5m,且水平放置;金属棒b和c可在轨道上无摩擦地滑动,两金属棒的质量mb=mc=0.1kg,电阻Rb=RC=1?,轨道的电阻不计.整个装置放在磁感强度B=1T的匀强磁场中,磁场方向与轨道平面垂直(如图).若使b棒以初速度V0=10m/s开始向右运动,求:
(1)c棒的最大加速度;
(2)c棒的最大速度。
B
M
c
b
N
类型三:磁场中的动量守恒问题
解析:
(1)刚开始运动时回路中的感应电流为:
刚开始运动时C棒的加速度最大:
c
b
B
M
N
(2)在磁场力的作用下,b棒做减速运动,当两棒速度相等时,c棒达到最大速度。取两棒为研究对象,根据动量守恒定律有:
解得c棒的最大速度为:
c
b
B
M
N
如图示,在光滑的水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态,质量为2m的小球A以初速度v0向右运动,接着逐渐压缩弹簧并使B运动,过了一段时间A与弹簧分离.
(1)当弹簧被压缩到最短时,弹簧的弹性势能EP多大?
(2)若开始时在B球的右侧某位置固定一块挡板,在A球与弹簧未分离前使B球与挡板发生碰撞,并在碰后立即将挡板撤走,设B球与挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反,欲使此后弹簧被压缩到最短时,弹性势能达到第(1)问中EP的2.5倍,必须使B球在速度多大时与挡板发生碰撞?
例1.
v0
B
A
甲
类型一:弹簧类问题
解:
v0
B
A
甲
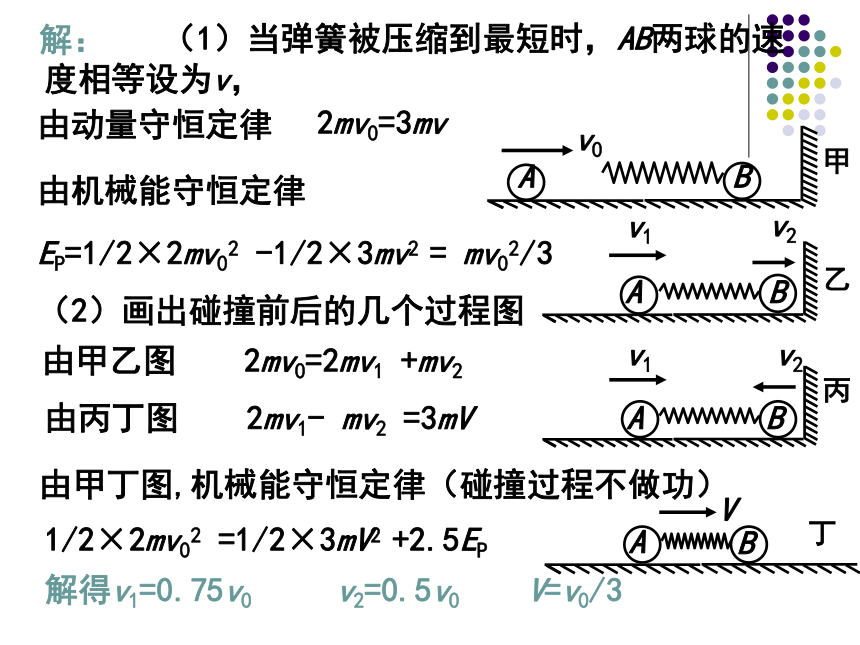
(1)当弹簧被压缩到最短时,AB两球的速度相等设为v,
由动量守恒定律
2mv0=3mv
由机械能守恒定律
EP=1/2×2mv02 -1/2×3mv2 = mv02/3
(2)画出碰撞前后的几个过程图
v1
B
A
v2
乙
A
B
v2
v1
丙
B
A
丁
V
由甲乙图 2mv0=2mv1 +mv2
由丙丁图 2mv1- mv2 =3mV
由甲丁图,机械能守恒定律(碰撞过程不做功)
1/2×2mv02 =1/2×3mV2 +2.5EP
解得v1=0.75v0 v2=0.5v0 V=v0/3
变式1:如图所示,光滑水平面上,轻弹簧两端分别拴住质量均为m的小物块A和B,B物块靠着竖直墙壁。今用水平外力缓慢推A,使A、B间弹簧压缩,当压缩到弹簧的弹性势能为E时撤去此水平外力,让A和B在水平面上运动.求:(1)当B离开墙壁时,A物块的速度大小;(2)当弹簧达到最大长度时A、B的速度大小;(3)当B离开墙壁以后的运动过程中,弹簧弹性势能的最大值.
F
小结:(1)“弹性势能最大时有共同速度”含义
(2)物理过程的分析。
(3)状态的选取。
变式1.如图,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上的O点,此时弹簧处于原长。另一质量与B相同的滑块A从导轨上的P点以初速度v0向B滑行,当A滑过距离l时,与B相碰。碰撞时间极短,碰后A、B粘在一起运动。设滑块A和B均可视为质点,与导轨的动摩擦因数均为μ 。重力加速度为g。求:
(1)碰后瞬间,A、B共同的速度大小;
(2)若A、B压缩弹簧后恰能返回到O点并停止,求弹簧的最大压缩量。
l
P
O
A
B
v0
解:
(1)设A、B质量均为m,A刚接触B时的速度为v1,碰后瞬间共同的速度为v2 以A为研究对象,从P到O,由功能关系
以A、B为研究对象,碰撞瞬间,由动量守恒定律
mv1 = 2mv2
解得
(2)碰后A、B由O点向左运动,又返回到O点,设弹簧的最大压缩量为x
由功能关系
解得
广东省重点中学12月月考检测题17
变式2:如图所示是某游乐场过山车的娱乐装置原理图,弧形轨道末端与一个半径为R的光滑圆轨道平滑连接,两辆质量均为m的相同小车(大小可忽略),中间夹住一轻弹簧后连接在一起,两车从光滑弧形轨道上的某一高度由静止滑下,当两车刚滑入圆环最低点时连接两车的挂钩突然断开,弹簧将两车弹开,其中后车刚好停下,前车沿圆环轨道运动恰能越过圆弧轨道最高点,求:
(1)前车被弹出时的速度;
(2)前车被弹出的过程中弹簧
释放的弹性势能;
(3)两车从静止下滑到最低点
的高度h。
h
R
类型二:动量守恒定律与机械能守恒定律结合
解:
(1)设前车在最高点速度为v2,依题意有
设前车在最低位置与后车分离后速度为v1,根据机械能守恒
由①②得:
(2)设两车分离前速度为v0,由动量守恒定律
2mv0 = mv1
设分离前弹簧弹性势能Ep,根据系统机械能守恒
(3)两车从h高处运动到最低处机械能守恒
题目
例、如图示,M为悬挂在竖直平面内某一点O的木质小球,(可以看作质点)悬线长为L,质量为m 的子弹以水平初速v0射入球在中而未穿出,要使子弹射入小球后,小球能在竖直平面内运动,悬线始终不发生松弛,求子弹的初速度v0的大小应满足的条件(不计空气阻力)
M
m
v0
O
解:
若小球能在竖直平面内作圆周运动,到最高点的速度为V
m1V2 / L ≥ m1 g 式中m1 =(M+m)
由机械能守恒定律 1/2m1V2+m1g×2L= 1/2m1V12
由动量守恒定律 m v0 = (M+m) V1
若小球只能在下半个圆周内作摆动
1/2m1V22 =m1gh ≤m1gL
类型三:子弹射木块类问题
类型三:滑块类问题
小结:滑块问题规律
(3)摩擦产生热量:Q=fS相,S相为相对滑行的距离.
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:(1)物体与小车保持相对静止时的速度;
(2)物体冲上小车后相对于小车板面滑动的距离。(3)物体从滑上小车到与车相对静止过程中物体对地的位移
(1)重视物理过程分析及受力分析
(2)“共速”后两者不再发生相对滑动
拓展:要使滑块C不滑出B,B至少要多少?
变式2、如图所示,质量为M的小车左端放一质量为m的物体.物体与小车之间的摩擦系数为μ,(M>m)现在小车与物体以速度v0在水平光滑地面上一起向右匀速运动.当小车与竖直墙壁发生弹性碰撞后,物体在小车上向右滑移一段距离后一起向左运动,求物体在小车上滑移的最大距离.
M
m
v0
解:小车碰墙后速度反向,由动量守恒定律
M
m
v0
v0
(M+m)V= (M-m)v0
最后速度为V,由能量守恒定律
M
m
V
V
1/2 (M+m)v0 2- 1/2 (M+m)V 2 =μmg S
拓展:若M
4. 在光滑的水平面上停放着质量为m、带有弧形槽的小车,现有一质量也为m的小球以v0 的水平速度沿槽口向小车滑去(不计摩擦),到达某一高度后,小球又返回车右端,则 ( )
A. 小球离车后,对地将向右做平抛运动
B. 小球离车后,对地将做自由落体运动
C. 此过程小球对车做功为mv0 2 / 2
D. 小球沿弧形槽上升的最大高度为v0 2 / 2g
B C
v0
?17.(16分)如图所示,光滑水平面上有一质量M=4.0kg的平板车,车的上表面右侧是一段长L=1.0m的水平轨道,水平轨道左侧连一半径R=0.25m的1/4光滑圆弧轨道,圆弧轨道与水平轨道在O′点相切.车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧,一质量m=1.0kg的小物块紧靠弹簧,小物块与水平轨道间的动摩擦因数μ=0.5。整个装置处于静止状态,现将弹簧解除锁定,小物块被弹出,恰能到达圆弧轨道的最高点A,g取10m/s2.求:
(1)解除锁定前弹簧的弹性势能;
(2)小物块第二次经过O′点
时的速度大小;
(3)最终小物块与车相对静止
时距O′点的距离.
A
R
M
O
O′
m
17.解:
⑴平板车和小物块组成的系统水平方向动量守恒,故小物块恰能到达圆弧最高点A时,
二者的共同速度 v共 =0 ①
设弹簧解除锁定前的弹性势能为EP,上述过程中系统能量守恒,则有
EP=mgR+μmgL ②
代入数据解得 EP =7.5 J ③
⑵设小物块第二次经过O′时的速度大小为vm,此时平板车的速度大小为vM ,研究小物块在圆弧面上下滑过程,由系统动量守恒和机械能守恒有
0=mvm -MvM ④
A
R
M
O
O'
m
⑤
由④、⑤式代入数据解得
vm=2.0 m/s ⑥
⑶最终平板车和小物块相对静止时,二者的共同
速度为0。
设小物块相对平板车滑动的总路程为S,
对系统由能量守恒有
EP=μmgS ⑦
代入数据解得 S=1.5 m ⑧
则距O′点的距离x=S-L=0.5 m ⑨
评分标准:本题共16分,①②式各2分,③式1分;
④⑤⑥式各2分;⑦⑧式各2分,⑨式1分。
题目
17、(20分)如图甲所示,质量为M、长L= 1.0m、右端带有竖直挡板的木板B静止在光滑水平面上,一个质量为m的小木块A(可视为质点),以水平速度v0=4.0 m/s滑上B的左端,而后与右端挡板碰撞,最后恰好滑到木板B的左端,已知M/m=3,并设A与挡板碰撞时无机械能损失,碰撞时间可以忽略,求;
(1)A、B最终的速度。
(2)木块A与木块B间的动摩擦因数。
(3)在图乙所给坐标中画出此过程中B相对地的v-t图线。(要写出分析和计算)
L
B
A
甲
0
v/ms-1
t/s
乙
2页
题目
3页
末页
解:
(1)对M、m系统相互作用的全过程,由动量守恒定律得
mv0 = (M+m) v
解得 v = 1 m/s
(2)A、B相互作用的全过程中,摩擦生热等于机械能的减少,即
解得 μ= 0.3
(3)研究A、B系统,从A滑上B至A相对B滑行距离为L的过程,由动量守恒和能量守恒可得
mv0 = m v1 + M v2
2页
题目
3页
末页
代入数据可得:
v1+3v2=4
v21 +3v22 =10
以上为A、B碰前瞬间的速度。
此为A、B刚碰后瞬间的速度。
2页
题目
3页
末页
木板B此过程为匀变速直线运动, B的加速度为
故碰前B加速时间为
碰后B减速时间为
故B对地的v~t图象如图所示。
v/ms-1
t/s
0
0.2 0.4 0.6 0.8 1.0 1.2
0.5
1.0
1.5
2.0
2.5
2页
题目
3页
末页
19.如图所示,质量为3m的足够长木板C静止在光滑水平面上,质量均为的两个小物块A、B放在C的左端,A、B间相距s0,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和2 μ ,则
(1)最终A、B、C的共同速度为多大?
(2)当与刚相对静止时的速度为多大?
(3)与最终相距多远?
(4)整个过程中A、B与木板C因摩擦所产生的热量之比为多大?
A
B
C
2页
题目
3页
4页
末页
解:
(1)由于A、B、C三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
于是可解得最终A、B、C的共同速度为:
( 2)设经t 时间A与C恰好相对静止,共同速度为vAC ,此时B的速度为vB,由
可解得:
2页
题目
3页
4页
末页
(3)在A与C相对静止前,三个物体的加速度大小分别为
A、B做匀减速运动,C做匀加速运动;在与相对静止后,三个物体的加速度大小又分别为
A、C做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动。
在开始运动到三个物体均相对静止的过程中、相对于地面的位移分别为
所以,A与B最终相距
2页
题目
3页
4页
末页
(4)设整个运动过程A相对于C滑行距离为s,
则B相对于C滑行的距离为
于是有
解得:
由此求得:整个过程中、与木板因摩擦所产生的
热量之比为
2页
题目
3页
4页
末页
类型四:磁场中的动量守恒问题
9、如图17-4所示,金属杆a在离地h高处从静止开始沿弧形轨道下滑,导轨平行的水平部分有竖直向上的匀强磁场B,水平部分导轨上原来放有一长L的金属杆b.已知a杆的质量为ma,且与b杆的质量比为ma∶mb = 3∶4,水平导轨足够长,不计摩擦.求:(1)若a、b电阻分别为Ra、Rb,则b的最大加速度为多大?(2)a和b的最终速度分别是多大?(3)整个过程中回路中释放的电能是多少?
方法小结:(1)刚开始时感应电动势E最大,电流最大,F安,a最大(2)双杆受到的安培力大小相等方向相反,系统动量守恒(3)求回路中释放热量用能量守恒方便
变式4:云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α 衰变, α 粒子的质量为m,电量为q, 其运动轨迹在与磁场垂直的平面内.现测得α 粒子运动的轨道半径R,试求在衰变过程中的质量亏损.(注:涉及动量问题时,亏损的质量可忽略不计.)
解: 令v 表示α粒子的速度,由洛仑兹力和牛顿定律可得qvB=mv2 /R
令V表示衰变后剩余核的速度,在考虑衰变过程中系统的动量守恒时,因为亏损质量很小,可不予考虑,
由动量守恒可知 (M-m)V=mv ②
返回
注意:(1)衰变过程动量守恒(2)注意质量关系和能量关系(3)在磁场中做圆周运动
问题2 在磁感强度为B的匀强磁场中有原来静止的铀核
和钍核
, 变式4 在磁感强度为B的匀强磁场中有原来静止的铀核 和钍核 。由于发生衰变而使生成物作匀速圆周运动.(1)试画出铀238发生α衰变时产生的α粒子及新核的运动轨迹示意图和钍234发生β衰变时产生β粒子及新核的运动轨迹示意图.(2)若铀核的质量为M,α粒子的质量为m,带电量为q,测得α粒子作圆周运动的轨道半径为R,反应过程中释放的能量全部转化为新核和α粒子的动能,求铀核衰变中的质量亏损.
解(1)放射性元素的衰变过程中动量守恒,根据动量守恒定定律可得:
(2)由于α粒子在磁场中运动的半径:
∴
由动量守恒可得新核运动的速度大小为:
反应中释放出的核能为:
根据质能联系方程可知质量亏损为:
α粒子
新核
β粒子
新核
返回
两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L。导轨上面横放着两根导体棒ab和cd,构成矩形回路,如图所示.两根导体棒的质量皆为m,电阻皆为R,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B.设两导体棒均可沿导轨无摩擦地滑行.开始时,棒cd静止,棒ab有指向棒cd的初速度v0.若两导体棒在运动中始终不接触,求:
(1)在运动中产生的焦耳热最多是多少.
(2)当ab棒的速度变为初速度的3/4时,cd棒的加速度是多少?
B
v0
L
a
c
d
b
如图所示,一质量为M、长为L的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块A,m<M. 现以地面为参照系,给A和B以大小相等、方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。
(1)若已知A和B的初速度大小为v0,求它们最后的速度大小和方向.
(2)若初速度的大小未知,求小木块A向左运动到达的最远处(从地面上看)离出发点的距离.
例1.
v0
v0
B
A
解:方法1、
v0
v0
B
A
用牛顿第二定律和运动学公式求解。
A刚好没有滑离B板,表示当A滑到B板的最左端时,A、B具有相同的速度,设此速度为v,经过时间为t, A、B间的滑动摩擦力为f. 如图所示。
L1
L2
L0
规定向右方向为正方向,则
对A据牛顿第二定律和运动学公式有:
f=maA ①
v=-v0+aAt ②
③
对B据牛顿第二定律和运动学公式有:
f=MaB ④
v=v0-aBt ⑤
由图示关系有:L0+(-L2)=L; ⑦
由①②④⑤得它们最后的速度为:
方向向右。
由②④得
代入③⑥⑦得
对A,向左运动的最大距离为
方法1
例1
3页
方法2
末页
5页
方法3
解:方法2、
v0
v0
B
A
用动能定理和动量定理求解。
A刚好没有滑离B板,表示当A滑到B板的最左端时,A、B具有相同的速度,设此速度为v,经过时间为t, A和B的初速度的大小为v0,设A与B之间的滑动摩擦力为f,则据动量定理可得:
L1
L2
L0
对A: f t= mv+mv0 ①
对B:-f t=Mv-Mv0 ②
解得:
方向向右
方法1
例1
3页
方法2
末页
5页
方法3
由动能定理:
对于B :
③
对于A :
④
⑤
由几何关系 L0+L2=L ⑥
由①②③④⑤⑥联立求得
方法1
例1
3页
方法2
末页
5页
方法3
解:方法3、
用能量守恒定律和动量守恒定律求解
A刚好没有滑离B板, 表示当A滑到B板的最左端时, A、B具有相同的速度,设此速度为v, A和B的初速度的大小为v0,则据动量守恒定律可得:
Mv0-mv0=(M+m)v
解得:
方向向右
对系统的全过程,由能量守恒定律得:
对于A
由上述二式联立求得
点评:从本题的三种解法可以看出:动量定理、动能定理与动量守恒定律、能量守恒定律,只研究一个物理过程的始末两个状态,与中间过程无关,对于中间过程复杂的问题,特别是变力问题,就显示出比牛顿定律的无比优越性。
方法1
例1
3页
方法2
末页
5页
方法3
17、(20分)如图甲所示,质量为M、长L= 1.0m、右端带有竖直挡板的木板B静止在光滑水平面上,一个质量为m的小木块A(可视为质点),以水平速度v0=4.0 m/s滑上B的左端,而后与右端挡板碰撞,最后恰好滑到木板B的左端,已知M/m=3,并设A与挡板碰撞时无机械能损失,碰撞时间可以忽略,求;
(1)A、B最终的速度。
(2)木块A与木块B间的动摩擦因数。
(3)在图乙所给坐标中画出此过程中B相对地的v-t图线。(要写出分析和计算)
L
B
A
甲
0
v/ms-1
t/s
乙
2页
题目
3页
末页
解:
(1)对M、m系统相互作用的全过程,由动量守恒定律得
mv0 = (M+m) v
解得 v = 1 m/s
(2)A、B相互作用的全过程中,摩擦生热等于机械能的减少,即
解得 μ= 0.3
(3)研究A、B系统,从A滑上B至A相对B滑行距离为L的过程,由动量守恒和能量守恒可得
mv0 = m v1 + M v2
2页
题目
3页
末页
代入数据可得:
v1+3v2=4
v21 +3v22 =10
以上为A、B碰前瞬间的速度。
此为A、B刚碰后瞬间的速度。
2页
题目
3页
末页
木板B此过程为匀变速直线运动, B的加速度为
故碰前B加速时间为
碰后B减速时间为
故B对地的v~t图象如图所示。
v/ms-1
t/s
0
0.2 0.4 0.6 0.8 1.0 1.2
0.5
1.0
1.5
2.0
2.5
2页
题目
3页
末页
19.如图所示,质量为3m的足够长木板C静止在光滑水平面上,质量均为的两个小物块A、B放在C的左端,A、B间相距s0,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和2 μ ,则
(1)最终A、B、C的共同速度为多大?
(2)当与刚相对静止时的速度为多大?
(3)与最终相距多远?
(4)整个过程中A、B与木板C因摩擦所产生的热量之比为多大?
A
B
C
2页
题目
3页
4页
末页
解:
(1)由于A、B、C三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
于是可解得最终A、B、C的共同速度为:
( 2)设经t 时间A与C恰好相对静止,共同速度为vAC ,此时B的速度为vB,由
可解得:
2页
题目
3页
4页
末页
(3)在A与C相对静止前,三个物体的加速度大小分别为
A、B做匀减速运动,C做匀加速运动;在与相对静止后,三个物体的加速度大小又分别为
A、C做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动。
2页
题目
3页
4页
末页
在开始运动到三个物体均相对静止的过程中、相对于地面的位移分别为
所以,A与B最终相距
2页
题目
3页
4页
末页
(4)设整个运动过程A相对于C滑行距离为s,
则B相对于C滑行的距离为
于是有
解得:
由此求得:整个过程中、与木板因摩擦所产生的
热量之比为
2页
题目
3页
4页
末页
等距双棒特点分析
1.电路特点
棒2相当于电源;棒1受安培力而加速起动,运动后产生反电动势.
2.电流特点
随着棒2的减速、棒1的加速,两棒的相对速度v2-v1变小,回路中电流也变小。
当v1=0时:
最大电流
当v2=v1时:
最小电流
两个极值
I=0
3.两棒的运动情况特点
安培力大小:
两棒的相对速度变小,感应电流变小,安培力变小.
棒1做加速度变小的加速运动
棒2做加速度变小的减速运动
v0
v共
t
O
v
最终两棒具有共同速度
4.两个规律
(1)动量规律
两棒受到安培力大小相等方向相反,
系统合外力为零,系统动量守恒.
(2)能量转化规律
系统机械能的减小量等于内能的增加量.
(类似于完全非弹性碰撞)
两棒产生焦耳热之比:
5.几种变化:
(1)初速度的提供方式不同
(2)磁场方向与导轨不垂直
(3)两棒都有初速度
v
v
0
0
1
1
2
2
(4)两棒位于不同磁场中
例2:如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有竖直向下方向的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:
(1)ab棒在N处进入磁场区速度多大?此时棒中电流是多少?
(2) cd棒能达到的最大速度是多大?
(3)ab棒由静止到达最大速度过程中,
系统所能释放的热量是多少?
解得:
进入磁场区瞬间,回路中电流强度I为
解析:
(1)ab棒由静止从M滑下到N的过程中,只有重力做功,机械能守恒,所以到N处速度可求,进而可求ab棒切割磁感线时产生的感应电动势和回路中的感应电流.
ab棒由M下滑到N过程中,机械能守恒,故有
(2)设ab棒与cd棒所受安培力的大小为F,安培力作用时间为 t,ab 棒在安培力作用下做减速运动,cd棒在安培力作用下做加速运动,当两棒速度达到相同速度v’时,电路中电流为零,安培力为零,cd达到最大速度.
运用动量守恒定律得:
解得
(3)系统释放热量应等于系统机械能减少量,故有:
解得
18.如图所示,质量为M=4kg的木板静止置于足够大的水平面上,木板与水平面间的动摩擦因数μ=0.01,板上最左端停放着质量为m=1kg可视为质点的电动小车,车与木板的档板相距L=5m,车由静止开始从木板左端向右做匀加速运动,经时间t=2s,车与挡板相碰,碰撞时间极短且碰后电动机的电源切断,车与挡板粘合在一起,求:
(1)试通过计算说明,电动小车在木板上运动时,木板能否保持静止?
(2)试求出碰后木板在水平面上滑动的距离。
L
m
M
2页
题目
3页
末页
解:
(1)设木板不动,电动车在板上运的加速度为a0
由
得
此时木板使车向右运动的摩擦力
木板受车向左的反作用力
木板受地面向右最大静摩擦力
所以木板不可能静止,将向左运动
2页
题目
3页
末页
(2)设电动车向右运动加速度a1,木板向左运动加速度为a2,碰前电动车速度为v1,木板速度为v2,碰后共同速度为v,两者一起向右运动s而停止。
对电动车
对木板
F' =F
又
解得
2页
题目
3页
末页
两者相碰时,动量守恒
根据动能定理:
解得: S=0.2 m
2页
题目
3页
末页
17.质量为M的小车置于水平面上。小车的上表面由1/4圆弧和平面组成,车的右端固定有一不计质量的弹簧,圆弧AB部分光滑,半径为R,平面BC部分粗糙,长为l,C点右方的平面光滑。滑块质量为m ,从圆弧最高处A无初速下滑(如图),与弹簧相接触并压缩弹簧,最后又返回到B相对于车静止。求:
(1)BC部分的动摩擦因数 ;
(2)弹簧具有的最大弹性势能;
(3)当滑块与弹簧刚分离时
滑块和小车的速度大小.
R
M
A
B
C
m
解:
(1) 对全过程,由动能定理得
(2)弹簧具有的最大弹性势能
(3)由机械能守恒定律
由动量守恒定律
解得:
16.1如图所示,光滑水平面上放置质量均为M=2kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5。一根通过细线拴着而被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧储存的弹性势能E0=10J,弹簧原长小于甲车长度,整个系统处于静止。现剪断细线,求:
⑴滑块P滑上乙车前的瞬时速度的大小;
⑵滑块P滑上乙车后最终未滑离乙车,
P在乙车上滑行的距离为多大?
乙
甲
P
解:
⑴设滑块P滑上乙车前的速度为v,对整体应用动量守恒和能量关系有:
mv-2MV = 0
解之得 v = 4 m/s
⑵ 设滑块P和小车乙达到的共同速度v′,
对滑块P和小车乙有:
mv-MV = (m+M)v′
代入数据解之得:
18、(16分)如图所示,水平传送带AB足够长,质量为M=1kg的木块随传送带一起以v1=2 m/s的速度向左匀速运动(传送带的速度恒定),木块与传送带的摩擦因数μ=0.5,当木块运动到最左端A点时,一颗质量为m=20 g的子弹,以v0=300 m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50 m/s,设子弹射穿木块的时间极短,(g取10 m/s2)求:
(1)木块遭射击后远离A的最大距离;
(2)木块遭击后在传送带上
向左运动所经历的时间。
M
B
A
v1
v0
解:
M
B
A
v1
v0
(1)设木块遭击后的速度瞬间变为V,以水平向右为正方向,根据动量守恒定律得
代入数据解得 V=3 m/s,方向向右。
木块遭击后沿传送带向右匀减速滑动,
摩擦力
设木块远离A点的最大距离为S,此时木块的末速度为0,
根据动能定理得
(2)研究木块在传送带上向左运动的情况。
设木块向左加速到v1=2m/s时的位移为S1。
由动能定理得
由此可知,遭击木块在传送带上向左的运动过程分两个阶段:先向左加速运动一段时间t1,再匀速运动一段时间t2
由动量定理得
所求时间
题目
动量与能量综合问题
归类分析
类型一:动量守恒定律与机械能守恒定律结合
如图所示,质量为M=4kg的平板车静止在光滑水平面上,其左端固定着一根轻弹,质量为m=1kg的小物体以水平速度v0=5m/s从平板车右端滑上车,相对于平板车向左滑动了L=1m后把弹簧压缩到最短,然后又相对于平板车向右滑动到最右端而与之保持相对静止。求
(1)小物体与平板车间的动摩擦因数;
(2)这过程中弹性势能的最大值。
M
m
v0
类型二:弹簧类问题
例1.无限长的平行金属轨道M、N,相距L=0.5m,且水平放置;金属棒b和c可在轨道上无摩擦地滑动,两金属棒的质量mb=mc=0.1kg,电阻Rb=RC=1?,轨道的电阻不计.整个装置放在磁感强度B=1T的匀强磁场中,磁场方向与轨道平面垂直(如图).若使b棒以初速度V0=10m/s开始向右运动,求:
(1)c棒的最大加速度;
(2)c棒的最大速度。
B
M
c
b
N
类型三:磁场中的动量守恒问题
解析:
(1)刚开始运动时回路中的感应电流为:
刚开始运动时C棒的加速度最大:
c
b
B
M
N
(2)在磁场力的作用下,b棒做减速运动,当两棒速度相等时,c棒达到最大速度。取两棒为研究对象,根据动量守恒定律有:
解得c棒的最大速度为:
c
b
B
M
N
如图示,在光滑的水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态,质量为2m的小球A以初速度v0向右运动,接着逐渐压缩弹簧并使B运动,过了一段时间A与弹簧分离.
(1)当弹簧被压缩到最短时,弹簧的弹性势能EP多大?
(2)若开始时在B球的右侧某位置固定一块挡板,在A球与弹簧未分离前使B球与挡板发生碰撞,并在碰后立即将挡板撤走,设B球与挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反,欲使此后弹簧被压缩到最短时,弹性势能达到第(1)问中EP的2.5倍,必须使B球在速度多大时与挡板发生碰撞?
例1.
v0
B
A
甲
类型一:弹簧类问题
解:
v0
B
A
甲
(1)当弹簧被压缩到最短时,AB两球的速度相等设为v,
由动量守恒定律
2mv0=3mv
由机械能守恒定律
EP=1/2×2mv02 -1/2×3mv2 = mv02/3
(2)画出碰撞前后的几个过程图
v1
B
A
v2
乙
A
B
v2
v1
丙
B
A
丁
V
由甲乙图 2mv0=2mv1 +mv2
由丙丁图 2mv1- mv2 =3mV
由甲丁图,机械能守恒定律(碰撞过程不做功)
1/2×2mv02 =1/2×3mV2 +2.5EP
解得v1=0.75v0 v2=0.5v0 V=v0/3
变式1:如图所示,光滑水平面上,轻弹簧两端分别拴住质量均为m的小物块A和B,B物块靠着竖直墙壁。今用水平外力缓慢推A,使A、B间弹簧压缩,当压缩到弹簧的弹性势能为E时撤去此水平外力,让A和B在水平面上运动.求:(1)当B离开墙壁时,A物块的速度大小;(2)当弹簧达到最大长度时A、B的速度大小;(3)当B离开墙壁以后的运动过程中,弹簧弹性势能的最大值.
F
小结:(1)“弹性势能最大时有共同速度”含义
(2)物理过程的分析。
(3)状态的选取。
变式1.如图,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上的O点,此时弹簧处于原长。另一质量与B相同的滑块A从导轨上的P点以初速度v0向B滑行,当A滑过距离l时,与B相碰。碰撞时间极短,碰后A、B粘在一起运动。设滑块A和B均可视为质点,与导轨的动摩擦因数均为μ 。重力加速度为g。求:
(1)碰后瞬间,A、B共同的速度大小;
(2)若A、B压缩弹簧后恰能返回到O点并停止,求弹簧的最大压缩量。
l
P
O
A
B
v0
解:
(1)设A、B质量均为m,A刚接触B时的速度为v1,碰后瞬间共同的速度为v2 以A为研究对象,从P到O,由功能关系
以A、B为研究对象,碰撞瞬间,由动量守恒定律
mv1 = 2mv2
解得
(2)碰后A、B由O点向左运动,又返回到O点,设弹簧的最大压缩量为x
由功能关系
解得
广东省重点中学12月月考检测题17
变式2:如图所示是某游乐场过山车的娱乐装置原理图,弧形轨道末端与一个半径为R的光滑圆轨道平滑连接,两辆质量均为m的相同小车(大小可忽略),中间夹住一轻弹簧后连接在一起,两车从光滑弧形轨道上的某一高度由静止滑下,当两车刚滑入圆环最低点时连接两车的挂钩突然断开,弹簧将两车弹开,其中后车刚好停下,前车沿圆环轨道运动恰能越过圆弧轨道最高点,求:
(1)前车被弹出时的速度;
(2)前车被弹出的过程中弹簧
释放的弹性势能;
(3)两车从静止下滑到最低点
的高度h。
h
R
类型二:动量守恒定律与机械能守恒定律结合
解:
(1)设前车在最高点速度为v2,依题意有
设前车在最低位置与后车分离后速度为v1,根据机械能守恒
由①②得:
(2)设两车分离前速度为v0,由动量守恒定律
2mv0 = mv1
设分离前弹簧弹性势能Ep,根据系统机械能守恒
(3)两车从h高处运动到最低处机械能守恒
题目
例、如图示,M为悬挂在竖直平面内某一点O的木质小球,(可以看作质点)悬线长为L,质量为m 的子弹以水平初速v0射入球在中而未穿出,要使子弹射入小球后,小球能在竖直平面内运动,悬线始终不发生松弛,求子弹的初速度v0的大小应满足的条件(不计空气阻力)
M
m
v0
O
解:
若小球能在竖直平面内作圆周运动,到最高点的速度为V
m1V2 / L ≥ m1 g 式中m1 =(M+m)
由机械能守恒定律 1/2m1V2+m1g×2L= 1/2m1V12
由动量守恒定律 m v0 = (M+m) V1
若小球只能在下半个圆周内作摆动
1/2m1V22 =m1gh ≤m1gL
类型三:子弹射木块类问题
类型三:滑块类问题
小结:滑块问题规律
(3)摩擦产生热量:Q=fS相,S相为相对滑行的距离.
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:(1)物体与小车保持相对静止时的速度;
(2)物体冲上小车后相对于小车板面滑动的距离。(3)物体从滑上小车到与车相对静止过程中物体对地的位移
(1)重视物理过程分析及受力分析
(2)“共速”后两者不再发生相对滑动
拓展:要使滑块C不滑出B,B至少要多少?
变式2、如图所示,质量为M的小车左端放一质量为m的物体.物体与小车之间的摩擦系数为μ,(M>m)现在小车与物体以速度v0在水平光滑地面上一起向右匀速运动.当小车与竖直墙壁发生弹性碰撞后,物体在小车上向右滑移一段距离后一起向左运动,求物体在小车上滑移的最大距离.
M
m
v0
解:小车碰墙后速度反向,由动量守恒定律
M
m
v0
v0
(M+m)V= (M-m)v0
最后速度为V,由能量守恒定律
M
m
V
V
1/2 (M+m)v0 2- 1/2 (M+m)V 2 =μmg S
拓展:若M
4. 在光滑的水平面上停放着质量为m、带有弧形槽的小车,现有一质量也为m的小球以v0 的水平速度沿槽口向小车滑去(不计摩擦),到达某一高度后,小球又返回车右端,则 ( )
A. 小球离车后,对地将向右做平抛运动
B. 小球离车后,对地将做自由落体运动
C. 此过程小球对车做功为mv0 2 / 2
D. 小球沿弧形槽上升的最大高度为v0 2 / 2g
B C
v0
?17.(16分)如图所示,光滑水平面上有一质量M=4.0kg的平板车,车的上表面右侧是一段长L=1.0m的水平轨道,水平轨道左侧连一半径R=0.25m的1/4光滑圆弧轨道,圆弧轨道与水平轨道在O′点相切.车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧,一质量m=1.0kg的小物块紧靠弹簧,小物块与水平轨道间的动摩擦因数μ=0.5。整个装置处于静止状态,现将弹簧解除锁定,小物块被弹出,恰能到达圆弧轨道的最高点A,g取10m/s2.求:
(1)解除锁定前弹簧的弹性势能;
(2)小物块第二次经过O′点
时的速度大小;
(3)最终小物块与车相对静止
时距O′点的距离.
A
R
M
O
O′
m
17.解:
⑴平板车和小物块组成的系统水平方向动量守恒,故小物块恰能到达圆弧最高点A时,
二者的共同速度 v共 =0 ①
设弹簧解除锁定前的弹性势能为EP,上述过程中系统能量守恒,则有
EP=mgR+μmgL ②
代入数据解得 EP =7.5 J ③
⑵设小物块第二次经过O′时的速度大小为vm,此时平板车的速度大小为vM ,研究小物块在圆弧面上下滑过程,由系统动量守恒和机械能守恒有
0=mvm -MvM ④
A
R
M
O
O'
m
⑤
由④、⑤式代入数据解得
vm=2.0 m/s ⑥
⑶最终平板车和小物块相对静止时,二者的共同
速度为0。
设小物块相对平板车滑动的总路程为S,
对系统由能量守恒有
EP=μmgS ⑦
代入数据解得 S=1.5 m ⑧
则距O′点的距离x=S-L=0.5 m ⑨
评分标准:本题共16分,①②式各2分,③式1分;
④⑤⑥式各2分;⑦⑧式各2分,⑨式1分。
题目
17、(20分)如图甲所示,质量为M、长L= 1.0m、右端带有竖直挡板的木板B静止在光滑水平面上,一个质量为m的小木块A(可视为质点),以水平速度v0=4.0 m/s滑上B的左端,而后与右端挡板碰撞,最后恰好滑到木板B的左端,已知M/m=3,并设A与挡板碰撞时无机械能损失,碰撞时间可以忽略,求;
(1)A、B最终的速度。
(2)木块A与木块B间的动摩擦因数。
(3)在图乙所给坐标中画出此过程中B相对地的v-t图线。(要写出分析和计算)
L
B
A
甲
0
v/ms-1
t/s
乙
2页
题目
3页
末页
解:
(1)对M、m系统相互作用的全过程,由动量守恒定律得
mv0 = (M+m) v
解得 v = 1 m/s
(2)A、B相互作用的全过程中,摩擦生热等于机械能的减少,即
解得 μ= 0.3
(3)研究A、B系统,从A滑上B至A相对B滑行距离为L的过程,由动量守恒和能量守恒可得
mv0 = m v1 + M v2
2页
题目
3页
末页
代入数据可得:
v1+3v2=4
v21 +3v22 =10
以上为A、B碰前瞬间的速度。
此为A、B刚碰后瞬间的速度。
2页
题目
3页
末页
木板B此过程为匀变速直线运动, B的加速度为
故碰前B加速时间为
碰后B减速时间为
故B对地的v~t图象如图所示。
v/ms-1
t/s
0
0.2 0.4 0.6 0.8 1.0 1.2
0.5
1.0
1.5
2.0
2.5
2页
题目
3页
末页
19.如图所示,质量为3m的足够长木板C静止在光滑水平面上,质量均为的两个小物块A、B放在C的左端,A、B间相距s0,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和2 μ ,则
(1)最终A、B、C的共同速度为多大?
(2)当与刚相对静止时的速度为多大?
(3)与最终相距多远?
(4)整个过程中A、B与木板C因摩擦所产生的热量之比为多大?
A
B
C
2页
题目
3页
4页
末页
解:
(1)由于A、B、C三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
于是可解得最终A、B、C的共同速度为:
( 2)设经t 时间A与C恰好相对静止,共同速度为vAC ,此时B的速度为vB,由
可解得:
2页
题目
3页
4页
末页
(3)在A与C相对静止前,三个物体的加速度大小分别为
A、B做匀减速运动,C做匀加速运动;在与相对静止后,三个物体的加速度大小又分别为
A、C做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动。
在开始运动到三个物体均相对静止的过程中、相对于地面的位移分别为
所以,A与B最终相距
2页
题目
3页
4页
末页
(4)设整个运动过程A相对于C滑行距离为s,
则B相对于C滑行的距离为
于是有
解得:
由此求得:整个过程中、与木板因摩擦所产生的
热量之比为
2页
题目
3页
4页
末页
类型四:磁场中的动量守恒问题
9、如图17-4所示,金属杆a在离地h高处从静止开始沿弧形轨道下滑,导轨平行的水平部分有竖直向上的匀强磁场B,水平部分导轨上原来放有一长L的金属杆b.已知a杆的质量为ma,且与b杆的质量比为ma∶mb = 3∶4,水平导轨足够长,不计摩擦.求:(1)若a、b电阻分别为Ra、Rb,则b的最大加速度为多大?(2)a和b的最终速度分别是多大?(3)整个过程中回路中释放的电能是多少?
方法小结:(1)刚开始时感应电动势E最大,电流最大,F安,a最大(2)双杆受到的安培力大小相等方向相反,系统动量守恒(3)求回路中释放热量用能量守恒方便
变式4:云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α 衰变, α 粒子的质量为m,电量为q, 其运动轨迹在与磁场垂直的平面内.现测得α 粒子运动的轨道半径R,试求在衰变过程中的质量亏损.(注:涉及动量问题时,亏损的质量可忽略不计.)
解: 令v 表示α粒子的速度,由洛仑兹力和牛顿定律可得qvB=mv2 /R
令V表示衰变后剩余核的速度,在考虑衰变过程中系统的动量守恒时,因为亏损质量很小,可不予考虑,
由动量守恒可知 (M-m)V=mv ②
返回
注意:(1)衰变过程动量守恒(2)注意质量关系和能量关系(3)在磁场中做圆周运动
问题2 在磁感强度为B的匀强磁场中有原来静止的铀核
和钍核
, 变式4 在磁感强度为B的匀强磁场中有原来静止的铀核 和钍核 。由于发生衰变而使生成物作匀速圆周运动.(1)试画出铀238发生α衰变时产生的α粒子及新核的运动轨迹示意图和钍234发生β衰变时产生β粒子及新核的运动轨迹示意图.(2)若铀核的质量为M,α粒子的质量为m,带电量为q,测得α粒子作圆周运动的轨道半径为R,反应过程中释放的能量全部转化为新核和α粒子的动能,求铀核衰变中的质量亏损.
解(1)放射性元素的衰变过程中动量守恒,根据动量守恒定定律可得:
(2)由于α粒子在磁场中运动的半径:
∴
由动量守恒可得新核运动的速度大小为:
反应中释放出的核能为:
根据质能联系方程可知质量亏损为:
α粒子
新核
β粒子
新核
返回
两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L。导轨上面横放着两根导体棒ab和cd,构成矩形回路,如图所示.两根导体棒的质量皆为m,电阻皆为R,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B.设两导体棒均可沿导轨无摩擦地滑行.开始时,棒cd静止,棒ab有指向棒cd的初速度v0.若两导体棒在运动中始终不接触,求:
(1)在运动中产生的焦耳热最多是多少.
(2)当ab棒的速度变为初速度的3/4时,cd棒的加速度是多少?
B
v0
L
a
c
d
b
如图所示,一质量为M、长为L的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块A,m<M. 现以地面为参照系,给A和B以大小相等、方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。
(1)若已知A和B的初速度大小为v0,求它们最后的速度大小和方向.
(2)若初速度的大小未知,求小木块A向左运动到达的最远处(从地面上看)离出发点的距离.
例1.
v0
v0
B
A
解:方法1、
v0
v0
B
A
用牛顿第二定律和运动学公式求解。
A刚好没有滑离B板,表示当A滑到B板的最左端时,A、B具有相同的速度,设此速度为v,经过时间为t, A、B间的滑动摩擦力为f. 如图所示。
L1
L2
L0
规定向右方向为正方向,则
对A据牛顿第二定律和运动学公式有:
f=maA ①
v=-v0+aAt ②
③
对B据牛顿第二定律和运动学公式有:
f=MaB ④
v=v0-aBt ⑤
由图示关系有:L0+(-L2)=L; ⑦
由①②④⑤得它们最后的速度为:
方向向右。
由②④得
代入③⑥⑦得
对A,向左运动的最大距离为
方法1
例1
3页
方法2
末页
5页
方法3
解:方法2、
v0
v0
B
A
用动能定理和动量定理求解。
A刚好没有滑离B板,表示当A滑到B板的最左端时,A、B具有相同的速度,设此速度为v,经过时间为t, A和B的初速度的大小为v0,设A与B之间的滑动摩擦力为f,则据动量定理可得:
L1
L2
L0
对A: f t= mv+mv0 ①
对B:-f t=Mv-Mv0 ②
解得:
方向向右
方法1
例1
3页
方法2
末页
5页
方法3
由动能定理:
对于B :
③
对于A :
④
⑤
由几何关系 L0+L2=L ⑥
由①②③④⑤⑥联立求得
方法1
例1
3页
方法2
末页
5页
方法3
解:方法3、
用能量守恒定律和动量守恒定律求解
A刚好没有滑离B板, 表示当A滑到B板的最左端时, A、B具有相同的速度,设此速度为v, A和B的初速度的大小为v0,则据动量守恒定律可得:
Mv0-mv0=(M+m)v
解得:
方向向右
对系统的全过程,由能量守恒定律得:
对于A
由上述二式联立求得
点评:从本题的三种解法可以看出:动量定理、动能定理与动量守恒定律、能量守恒定律,只研究一个物理过程的始末两个状态,与中间过程无关,对于中间过程复杂的问题,特别是变力问题,就显示出比牛顿定律的无比优越性。
方法1
例1
3页
方法2
末页
5页
方法3
17、(20分)如图甲所示,质量为M、长L= 1.0m、右端带有竖直挡板的木板B静止在光滑水平面上,一个质量为m的小木块A(可视为质点),以水平速度v0=4.0 m/s滑上B的左端,而后与右端挡板碰撞,最后恰好滑到木板B的左端,已知M/m=3,并设A与挡板碰撞时无机械能损失,碰撞时间可以忽略,求;
(1)A、B最终的速度。
(2)木块A与木块B间的动摩擦因数。
(3)在图乙所给坐标中画出此过程中B相对地的v-t图线。(要写出分析和计算)
L
B
A
甲
0
v/ms-1
t/s
乙
2页
题目
3页
末页
解:
(1)对M、m系统相互作用的全过程,由动量守恒定律得
mv0 = (M+m) v
解得 v = 1 m/s
(2)A、B相互作用的全过程中,摩擦生热等于机械能的减少,即
解得 μ= 0.3
(3)研究A、B系统,从A滑上B至A相对B滑行距离为L的过程,由动量守恒和能量守恒可得
mv0 = m v1 + M v2
2页
题目
3页
末页
代入数据可得:
v1+3v2=4
v21 +3v22 =10
以上为A、B碰前瞬间的速度。
此为A、B刚碰后瞬间的速度。
2页
题目
3页
末页
木板B此过程为匀变速直线运动, B的加速度为
故碰前B加速时间为
碰后B减速时间为
故B对地的v~t图象如图所示。
v/ms-1
t/s
0
0.2 0.4 0.6 0.8 1.0 1.2
0.5
1.0
1.5
2.0
2.5
2页
题目
3页
末页
19.如图所示,质量为3m的足够长木板C静止在光滑水平面上,质量均为的两个小物块A、B放在C的左端,A、B间相距s0,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和2 μ ,则
(1)最终A、B、C的共同速度为多大?
(2)当与刚相对静止时的速度为多大?
(3)与最终相距多远?
(4)整个过程中A、B与木板C因摩擦所产生的热量之比为多大?
A
B
C
2页
题目
3页
4页
末页
解:
(1)由于A、B、C三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
于是可解得最终A、B、C的共同速度为:
( 2)设经t 时间A与C恰好相对静止,共同速度为vAC ,此时B的速度为vB,由
可解得:
2页
题目
3页
4页
末页
(3)在A与C相对静止前,三个物体的加速度大小分别为
A、B做匀减速运动,C做匀加速运动;在与相对静止后,三个物体的加速度大小又分别为
A、C做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动。
2页
题目
3页
4页
末页
在开始运动到三个物体均相对静止的过程中、相对于地面的位移分别为
所以,A与B最终相距
2页
题目
3页
4页
末页
(4)设整个运动过程A相对于C滑行距离为s,
则B相对于C滑行的距离为
于是有
解得:
由此求得:整个过程中、与木板因摩擦所产生的
热量之比为
2页
题目
3页
4页
末页
等距双棒特点分析
1.电路特点
棒2相当于电源;棒1受安培力而加速起动,运动后产生反电动势.
2.电流特点
随着棒2的减速、棒1的加速,两棒的相对速度v2-v1变小,回路中电流也变小。
当v1=0时:
最大电流
当v2=v1时:
最小电流
两个极值
I=0
3.两棒的运动情况特点
安培力大小:
两棒的相对速度变小,感应电流变小,安培力变小.
棒1做加速度变小的加速运动
棒2做加速度变小的减速运动
v0
v共
t
O
v
最终两棒具有共同速度
4.两个规律
(1)动量规律
两棒受到安培力大小相等方向相反,
系统合外力为零,系统动量守恒.
(2)能量转化规律
系统机械能的减小量等于内能的增加量.
(类似于完全非弹性碰撞)
两棒产生焦耳热之比:
5.几种变化:
(1)初速度的提供方式不同
(2)磁场方向与导轨不垂直
(3)两棒都有初速度
v
v
0
0
1
1
2
2
(4)两棒位于不同磁场中
例2:如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有竖直向下方向的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:
(1)ab棒在N处进入磁场区速度多大?此时棒中电流是多少?
(2) cd棒能达到的最大速度是多大?
(3)ab棒由静止到达最大速度过程中,
系统所能释放的热量是多少?
解得:
进入磁场区瞬间,回路中电流强度I为
解析:
(1)ab棒由静止从M滑下到N的过程中,只有重力做功,机械能守恒,所以到N处速度可求,进而可求ab棒切割磁感线时产生的感应电动势和回路中的感应电流.
ab棒由M下滑到N过程中,机械能守恒,故有
(2)设ab棒与cd棒所受安培力的大小为F,安培力作用时间为 t,ab 棒在安培力作用下做减速运动,cd棒在安培力作用下做加速运动,当两棒速度达到相同速度v’时,电路中电流为零,安培力为零,cd达到最大速度.
运用动量守恒定律得:
解得
(3)系统释放热量应等于系统机械能减少量,故有:
解得
18.如图所示,质量为M=4kg的木板静止置于足够大的水平面上,木板与水平面间的动摩擦因数μ=0.01,板上最左端停放着质量为m=1kg可视为质点的电动小车,车与木板的档板相距L=5m,车由静止开始从木板左端向右做匀加速运动,经时间t=2s,车与挡板相碰,碰撞时间极短且碰后电动机的电源切断,车与挡板粘合在一起,求:
(1)试通过计算说明,电动小车在木板上运动时,木板能否保持静止?
(2)试求出碰后木板在水平面上滑动的距离。
L
m
M
2页
题目
3页
末页
解:
(1)设木板不动,电动车在板上运的加速度为a0
由
得
此时木板使车向右运动的摩擦力
木板受车向左的反作用力
木板受地面向右最大静摩擦力
所以木板不可能静止,将向左运动
2页
题目
3页
末页
(2)设电动车向右运动加速度a1,木板向左运动加速度为a2,碰前电动车速度为v1,木板速度为v2,碰后共同速度为v,两者一起向右运动s而停止。
对电动车
对木板
F' =F
又
解得
2页
题目
3页
末页
两者相碰时,动量守恒
根据动能定理:
解得: S=0.2 m
2页
题目
3页
末页
17.质量为M的小车置于水平面上。小车的上表面由1/4圆弧和平面组成,车的右端固定有一不计质量的弹簧,圆弧AB部分光滑,半径为R,平面BC部分粗糙,长为l,C点右方的平面光滑。滑块质量为m ,从圆弧最高处A无初速下滑(如图),与弹簧相接触并压缩弹簧,最后又返回到B相对于车静止。求:
(1)BC部分的动摩擦因数 ;
(2)弹簧具有的最大弹性势能;
(3)当滑块与弹簧刚分离时
滑块和小车的速度大小.
R
M
A
B
C
m
解:
(1) 对全过程,由动能定理得
(2)弹簧具有的最大弹性势能
(3)由机械能守恒定律
由动量守恒定律
解得:
16.1如图所示,光滑水平面上放置质量均为M=2kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5。一根通过细线拴着而被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧储存的弹性势能E0=10J,弹簧原长小于甲车长度,整个系统处于静止。现剪断细线,求:
⑴滑块P滑上乙车前的瞬时速度的大小;
⑵滑块P滑上乙车后最终未滑离乙车,
P在乙车上滑行的距离为多大?
乙
甲
P
解:
⑴设滑块P滑上乙车前的速度为v,对整体应用动量守恒和能量关系有:
mv-2MV = 0
解之得 v = 4 m/s
⑵ 设滑块P和小车乙达到的共同速度v′,
对滑块P和小车乙有:
mv-MV = (m+M)v′
代入数据解之得:
18、(16分)如图所示,水平传送带AB足够长,质量为M=1kg的木块随传送带一起以v1=2 m/s的速度向左匀速运动(传送带的速度恒定),木块与传送带的摩擦因数μ=0.5,当木块运动到最左端A点时,一颗质量为m=20 g的子弹,以v0=300 m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50 m/s,设子弹射穿木块的时间极短,(g取10 m/s2)求:
(1)木块遭射击后远离A的最大距离;
(2)木块遭击后在传送带上
向左运动所经历的时间。
M
B
A
v1
v0
解:
M
B
A
v1
v0
(1)设木块遭击后的速度瞬间变为V,以水平向右为正方向,根据动量守恒定律得
代入数据解得 V=3 m/s,方向向右。
木块遭击后沿传送带向右匀减速滑动,
摩擦力
设木块远离A点的最大距离为S,此时木块的末速度为0,
根据动能定理得
(2)研究木块在传送带上向左运动的情况。
设木块向左加速到v1=2m/s时的位移为S1。
由动能定理得
由此可知,遭击木块在传送带上向左的运动过程分两个阶段:先向左加速运动一段时间t1,再匀速运动一段时间t2
由动量定理得
所求时间
题目
同课章节目录
