华东师大版八年级下册19.2菱形第1课时菱形的性质课件(共30张PPT)
文档属性
| 名称 | 华东师大版八年级下册19.2菱形第1课时菱形的性质课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-21 00:00:00 | ||
图片预览





文档简介
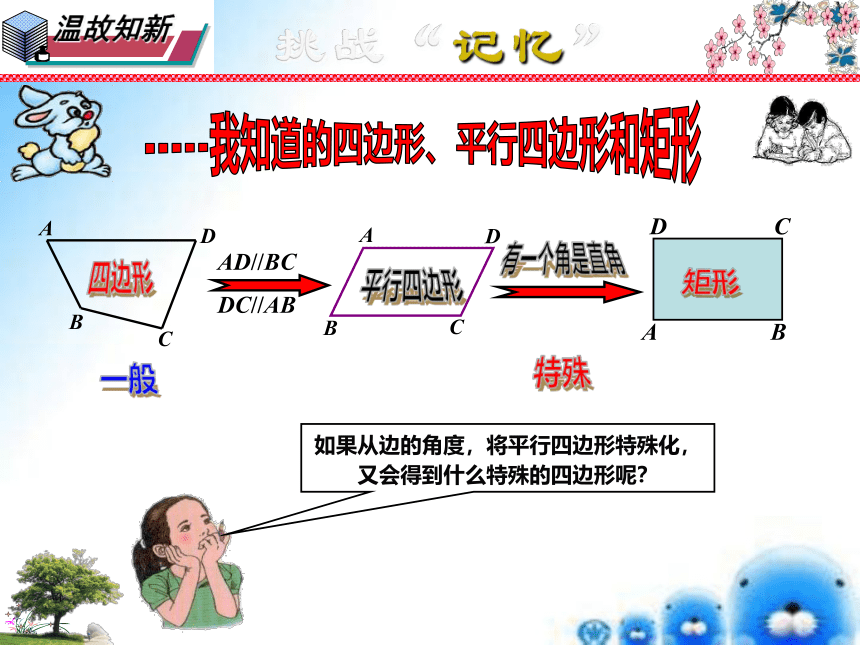
课件30张PPT。-----我知道的四边形、平行四边形和矩形AD//BC
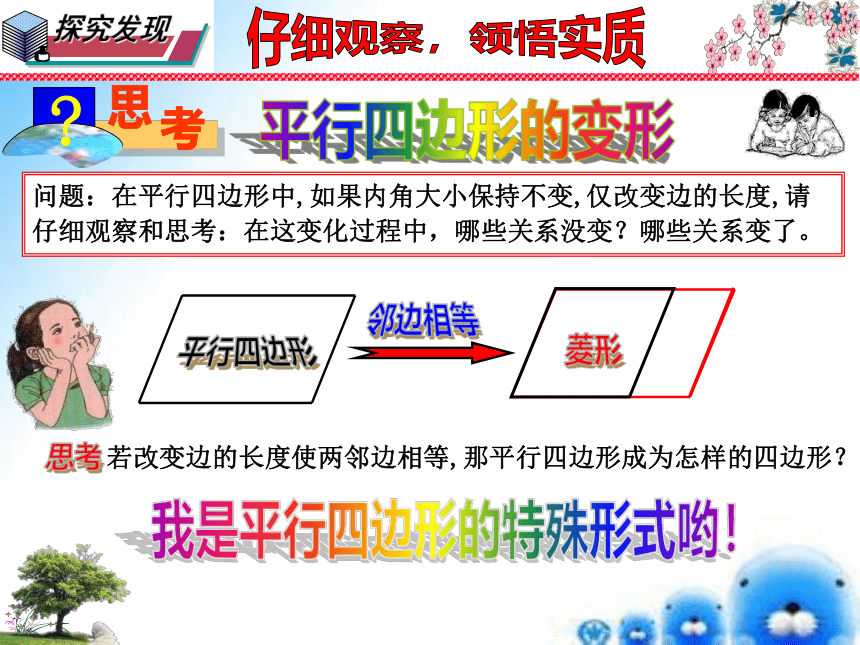
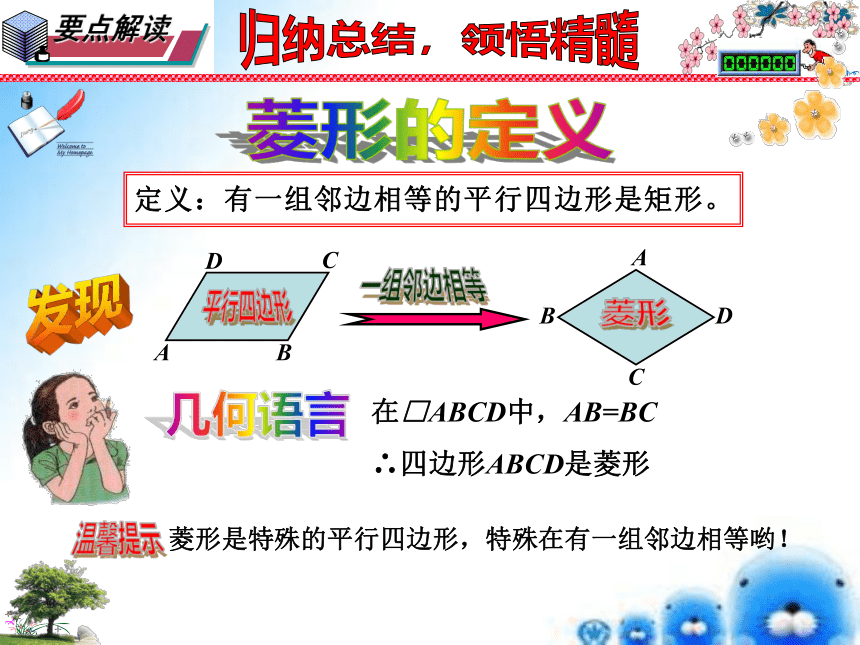
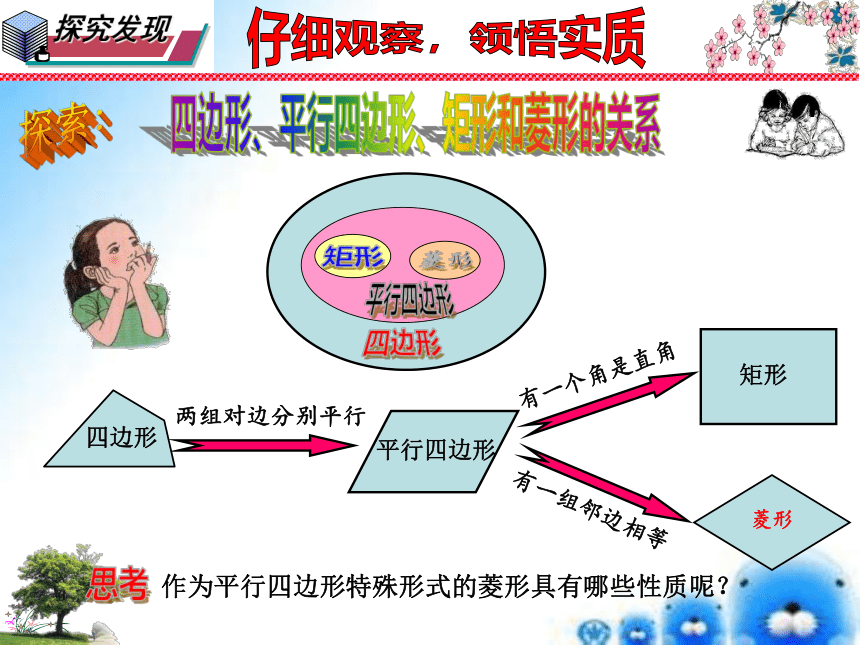
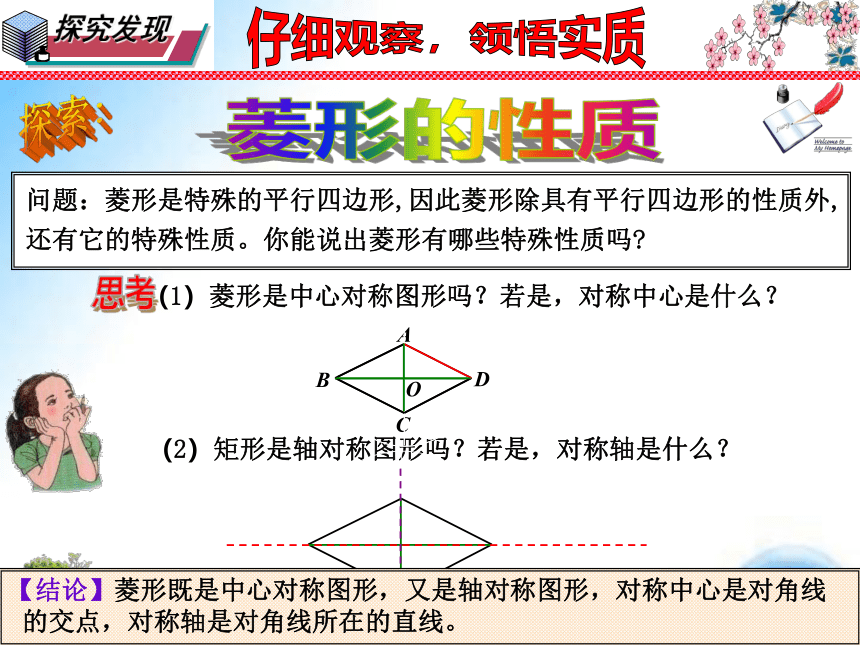
DC//AB一般特殊如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?仔细观察,领悟实质问题:在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了。平行四边形的变形我是平行四边形的特殊形式哟!邻边相等菱形归纳总结,领悟精髓菱形的定义定义:有一组邻边相等的平行四边形是矩形。平行四边形发现在□ABCD中,AB=BC ∴四边形ABCD是菱形几何语言仔细观察,领悟实质让我们共同走进生活中的菱形仔细观察,领悟实质2000多年前…… 一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑。菱形就在我们身边图片欣赏仔细观察,领悟实质探索:四边形、平行四边形、矩形和菱形的关系第1课时 菱形的性质19.2 菱形探索:仔细观察,领悟实质菱形的性质共性作为特殊的平行四边形,菱形具有哪些特有性质呢?平行四边形探索:仔细观察,领悟实质菱形的性质(2)矩形是轴对称图形吗?若是,对称轴是什么?【结论】菱形既是中心对称图形,又是轴对称图形,对称中心是对角线
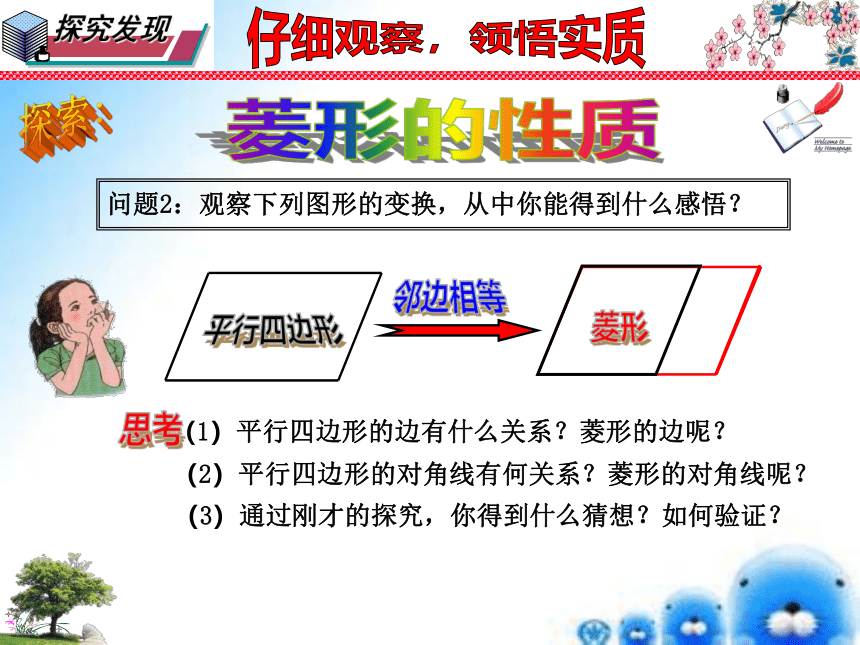
的交点,对称轴是对角线所在的直线。探索:仔细观察,领悟实质菱形的性质问题2:观察下列图形的变换,从中你能得到什么感悟?(2)平行四边形的对角线有何关系?菱形的对角线呢?(3)通过刚才的探究,你得到什么猜想?如何验证?邻边相等菱形探索:仔细观察,领悟实质猜想1:菱形的四条边都相等。已知:四边形ABCD是菱形, AB=BC
说明:AB=BC=CD=AD思路解析四边形ABCD是□AB=BC菱形的性质AB=DC
AD=BCAB=BC=CD=AD探索:仔细观察,领悟实质猜想2:菱形的对角线互相垂直。已知:四边形ABCD是菱形
说明:AC⊥BD思路解析菱形ABCDAB=AD
BO=DO菱形的性质AC⊥BD归纳总结,领悟精髓菱形的特殊性质菱形作为平行四边形的特殊性质,除了具有平行四边形所具有的一切性质外,还有如下特殊性质。
菱形的性质定理1:菱形的四条边都相等;
菱形的性质定理2:菱形的对角线相等。几何语言没有对比,就没有区别平行四边形、菱形对比理解对边平行
且相等四边都相等中心对称图形既是中心对称图形又是轴对称图形对角相等
邻角互补对角线互相平分对角线互相垂直探索:仔细观察,领悟实质问题:菱形是特殊的平行四边形,那么能否利用平行四边形的面积公式计算菱形的面积吗?菱形的面积公式E【菱形的面积公式】 S菱形 = 底×高 = 对角线乘积的一半如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F.(1)求证:△ADE≌△CDF;(2)若∠A=60°,求∠EDF的度数;(3)在(2)的基础上,若AE=1,求菱形ABCD的周长和面积。【变式】如图,在菱形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F.
AE=BE,求∠EDF的度数。学 以 致 用1.如图,菱形ABCD中,∠BAD=120°,若△ABC的周长为15,则菱形ABCD的周长是( )A、25 B、20 C、15 D、102.如图,在平面直角坐标系中,菱形OABC的顶点C的坐标是(3,4),则顶点A,B的坐标分别为( )A、(4,0),(7,4) B、(4,0),(8,4)
C、(5,0),(7,4) D、(5,0),(8,4)BD如图,在菱形ABCD中, ∠BAD=2∠B.(1)求∠B的度数;(2)试判断△ABC的形状,并说明理由;(3)若菱形的周长为40cm,求AC、BD的长;O【变式】已知菱形ABCD的边长为2cm,∠BAD=120。,对角线相交于
点O,试求这个菱形的两条对角线AC和BD的长。(结果保留根号)学 以 致 用1.菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等
C、对角线互相平分 D、对角线互相垂直D2.菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相垂直
C、对角线互相平分且相等 D、对角线互相平分D3.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( )A、20 B、24 C、40 D、48A学 以 致 用 4.如图,已知菱形ABCD的对角线相交于点O,延长AB至E,使得
BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50。,求∠BAO的度数。第1、2、3题中考链接(1)求点A的坐标;(2)求k的值。中考链接2.如图,点O是菱形ABCD对角线的交点,DE//AC,CE//BD,连结OE.(1)求证:OE=BC;(2)若四边形OCED的面积是8,求菱形ABCD的面积。中考链接3.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若点P为对角线BD上一动点,则EP+FP的最小值为( )A、1 B、2 C、3 D、4中考链接4.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形;(3)在(2)的条件下,如果AB=10,那么△AEF的周长是否存在最小值?
如果存在,请求出来。一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。谢谢 ,再见 !
DC//AB一般特殊如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?仔细观察,领悟实质问题:在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了。平行四边形的变形我是平行四边形的特殊形式哟!邻边相等菱形归纳总结,领悟精髓菱形的定义定义:有一组邻边相等的平行四边形是矩形。平行四边形发现在□ABCD中,AB=BC ∴四边形ABCD是菱形几何语言仔细观察,领悟实质让我们共同走进生活中的菱形仔细观察,领悟实质2000多年前…… 一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑。菱形就在我们身边图片欣赏仔细观察,领悟实质探索:四边形、平行四边形、矩形和菱形的关系第1课时 菱形的性质19.2 菱形探索:仔细观察,领悟实质菱形的性质共性作为特殊的平行四边形,菱形具有哪些特有性质呢?平行四边形探索:仔细观察,领悟实质菱形的性质(2)矩形是轴对称图形吗?若是,对称轴是什么?【结论】菱形既是中心对称图形,又是轴对称图形,对称中心是对角线
的交点,对称轴是对角线所在的直线。探索:仔细观察,领悟实质菱形的性质问题2:观察下列图形的变换,从中你能得到什么感悟?(2)平行四边形的对角线有何关系?菱形的对角线呢?(3)通过刚才的探究,你得到什么猜想?如何验证?邻边相等菱形探索:仔细观察,领悟实质猜想1:菱形的四条边都相等。已知:四边形ABCD是菱形, AB=BC
说明:AB=BC=CD=AD思路解析四边形ABCD是□AB=BC菱形的性质AB=DC
AD=BCAB=BC=CD=AD探索:仔细观察,领悟实质猜想2:菱形的对角线互相垂直。已知:四边形ABCD是菱形
说明:AC⊥BD思路解析菱形ABCDAB=AD
BO=DO菱形的性质AC⊥BD归纳总结,领悟精髓菱形的特殊性质菱形作为平行四边形的特殊性质,除了具有平行四边形所具有的一切性质外,还有如下特殊性质。
菱形的性质定理1:菱形的四条边都相等;
菱形的性质定理2:菱形的对角线相等。几何语言没有对比,就没有区别平行四边形、菱形对比理解对边平行
且相等四边都相等中心对称图形既是中心对称图形又是轴对称图形对角相等
邻角互补对角线互相平分对角线互相垂直探索:仔细观察,领悟实质问题:菱形是特殊的平行四边形,那么能否利用平行四边形的面积公式计算菱形的面积吗?菱形的面积公式E【菱形的面积公式】 S菱形 = 底×高 = 对角线乘积的一半如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F.(1)求证:△ADE≌△CDF;(2)若∠A=60°,求∠EDF的度数;(3)在(2)的基础上,若AE=1,求菱形ABCD的周长和面积。【变式】如图,在菱形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F.
AE=BE,求∠EDF的度数。学 以 致 用1.如图,菱形ABCD中,∠BAD=120°,若△ABC的周长为15,则菱形ABCD的周长是( )A、25 B、20 C、15 D、102.如图,在平面直角坐标系中,菱形OABC的顶点C的坐标是(3,4),则顶点A,B的坐标分别为( )A、(4,0),(7,4) B、(4,0),(8,4)
C、(5,0),(7,4) D、(5,0),(8,4)BD如图,在菱形ABCD中, ∠BAD=2∠B.(1)求∠B的度数;(2)试判断△ABC的形状,并说明理由;(3)若菱形的周长为40cm,求AC、BD的长;O【变式】已知菱形ABCD的边长为2cm,∠BAD=120。,对角线相交于
点O,试求这个菱形的两条对角线AC和BD的长。(结果保留根号)学 以 致 用1.菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等
C、对角线互相平分 D、对角线互相垂直D2.菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相垂直
C、对角线互相平分且相等 D、对角线互相平分D3.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( )A、20 B、24 C、40 D、48A学 以 致 用 4.如图,已知菱形ABCD的对角线相交于点O,延长AB至E,使得
BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50。,求∠BAO的度数。第1、2、3题中考链接(1)求点A的坐标;(2)求k的值。中考链接2.如图,点O是菱形ABCD对角线的交点,DE//AC,CE//BD,连结OE.(1)求证:OE=BC;(2)若四边形OCED的面积是8,求菱形ABCD的面积。中考链接3.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若点P为对角线BD上一动点,则EP+FP的最小值为( )A、1 B、2 C、3 D、4中考链接4.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形;(3)在(2)的条件下,如果AB=10,那么△AEF的周长是否存在最小值?
如果存在,请求出来。一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。谢谢 ,再见 !
