人教版五年级下教学课件第2节 长方体和正方体的表面积(51张ppt)
文档属性
| 名称 | 人教版五年级下教学课件第2节 长方体和正方体的表面积(51张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-21 15:21:56 | ||
图片预览


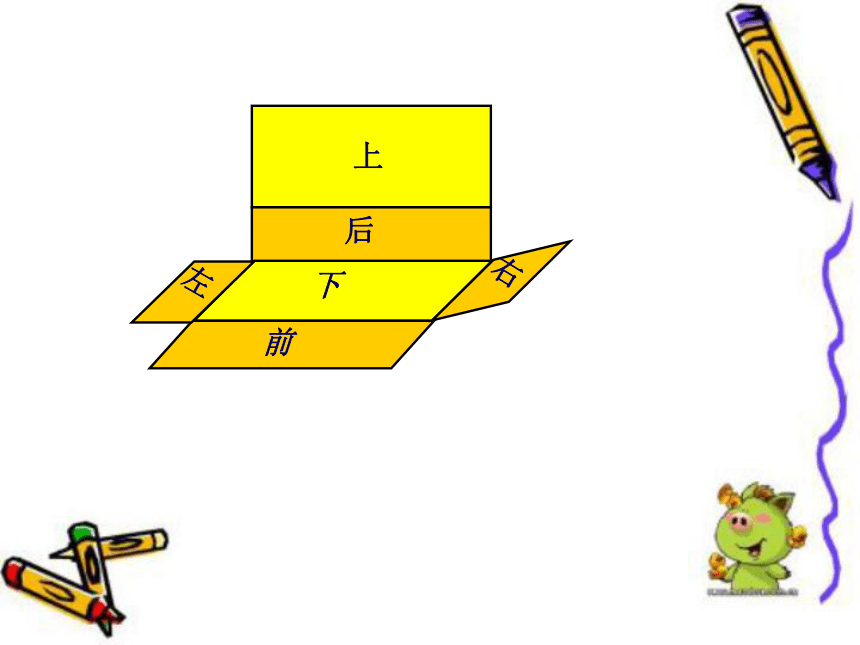
文档简介
(共51张PPT)
第3单元 长方体和正方体
五年级数学·下 新课标[人]
2 长方体和正方体的表面积
学习新知
随堂练习
作业设计
复习准备
复 习 准 备
返回目录
6cm
5cm
4cm
这个长方体:上、下两个面的长是( )cm,宽是( )cm。
前、后两个面的长是( )cm,宽是( )cm。
左、右两个面的长是( )cm,宽是( )cm。
6
5
6
4
5
4
学 习 新 知
物体表面的大小叫做物体的面积。
什么叫面积?
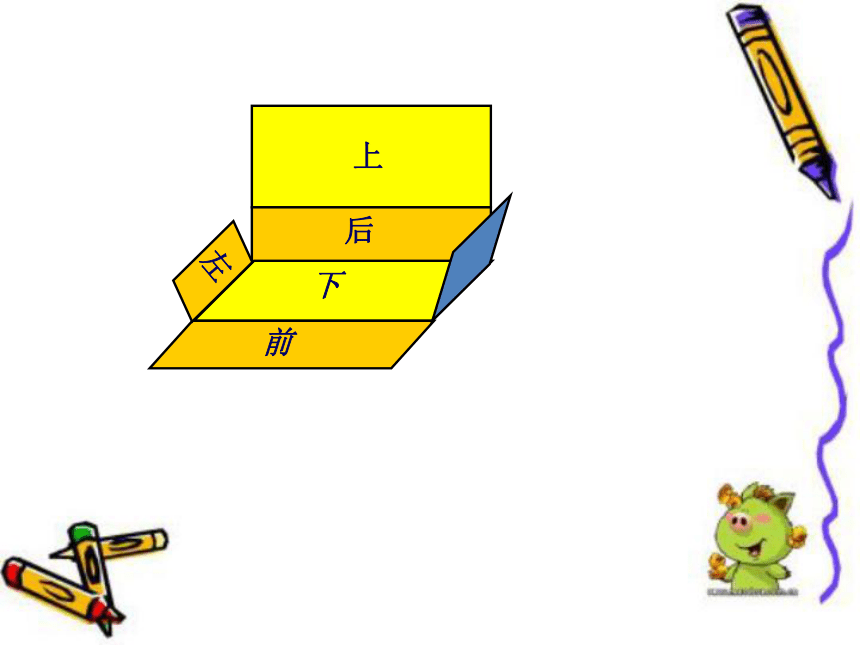
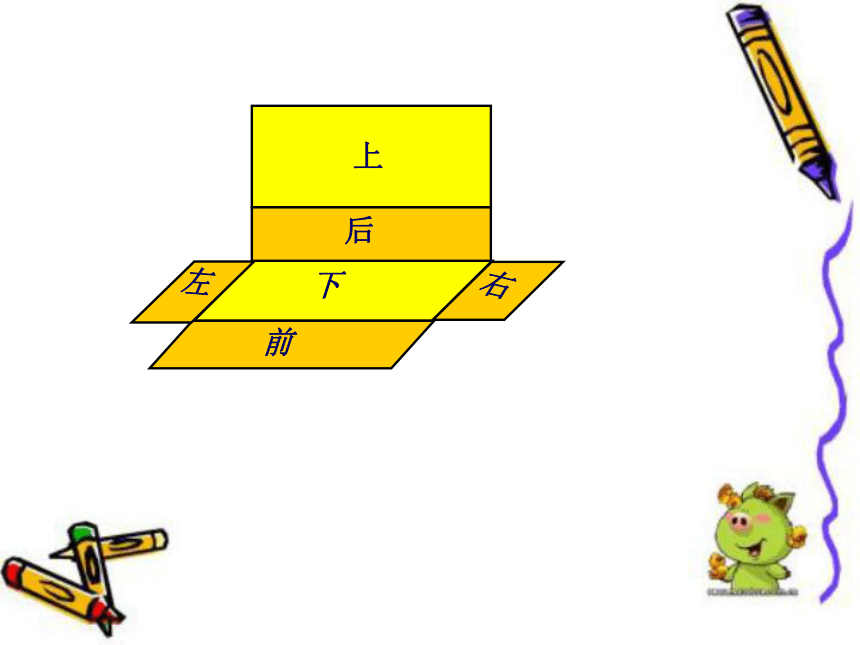
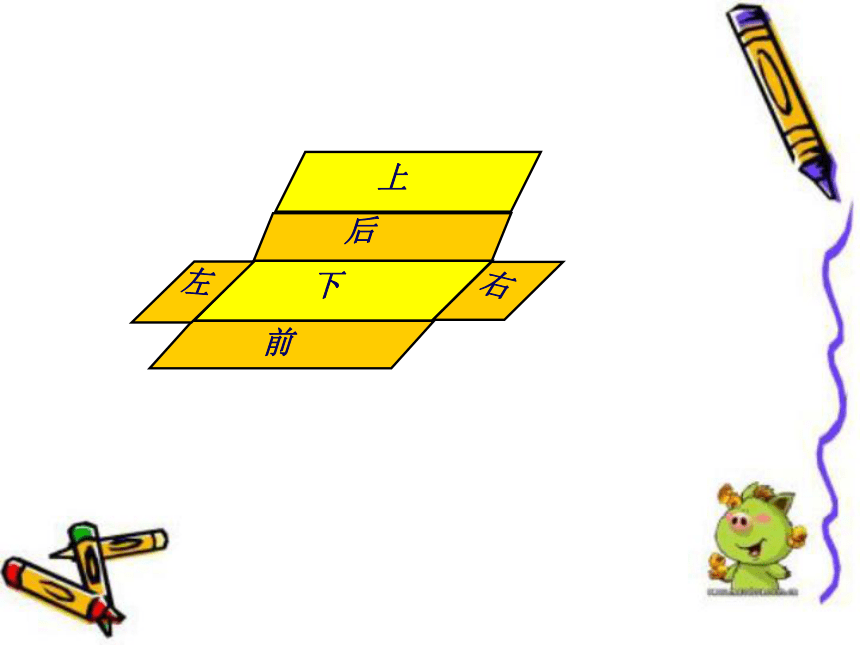
请你们拿出包装盒,沿着棱剪开,看看长方体和正方体的纸盒展开是什么形状。
小组里展示自己的展开图
在展开图中,分别用“上”“下”“前”
“后”“左”“右”标明6个面。
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
请在上面的展开图中,分别用“上”“下”
“前”“后”左”“右”标明6个面。
下
后
上
前
左
右
下
后
上
前
左
右
每个面的长和宽与长方体的长、宽、高有什么关系?
左面和右面
前、后两个面的长和宽分别是长方体的长和高,
下
后
上
前
左
右
观察长方体展开图,哪些面的面积相等?
上面和下面
前面和后面
上、下两个面的长和宽分别是长方体的长和宽,
左、右两个面的长和宽分别是长方体的宽和高。
折叠后,哪些图形能围成正方体?在括号中画“√”。
( )
练 习
( )
( )
√
√
摸一摸展开图每个面的大小。
长方体或正方体6个面的总面积,叫做它的表面积。
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
例1
要解决的问题与什么知识有关
要解决的问题与求长方体的表面积有关。
你获得了哪些信息
题中要求什么
微波炉的包装箱是一个长方体。
这个长方体的长是0.7 m,宽是0.5 m,高是0.4 m。
要求包装箱需要的硬纸板是多少平方米。
0.7m
0.5m
0.4m
前、后每个面,长______,宽_______,面积是__________;
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
例1
左、右每个面,长______,宽_______,面积是__________。
0.7m
0.5m
0.4m
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
这个包装箱的表面积是:
方法一:
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
= 0.7+0.56+0.4
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
例1
0.7m
0.5m
0.4m
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
这个包装箱的表面积是:
方法二:
(0.7×0.5+0.7×0.4+0.5×0.4)×2
= 0.83×2
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
例1
0.7m
0.5m
0.4m
长方体的表面积=(长×宽+长×高+高×宽)×2
(0.7×0.5+0.7×0.4+0.5×0.4)×2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
比较两种方法有什么不同,他们之间有什么联系?
上
和下
前
和后
右
和左
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
上(或下)
前(或后)
右(或左)
长方体的表面积=(长×宽+长×高+高×宽)×2
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
求出下图的表面积。
巩 固 练 习
解法1:
解法2:
解法3:
1.2×1.2×2+1.2×1×2+1.2×1×2
1.2×1.2×2+1.2×1×4=7.68(㎡)
(1.2×1.2+1.2×1+1.2×1)×2=7.68(㎡)
=2.88+2.4+2.4
=7.68(㎡)
6.5×6.5×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
6.5×6.5×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
写法一
6.5 ×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
写法二
小 结
正方体的表面积=棱长×棱长×6
正方体的表面积=棱长 ×6
求出各图的表面积。
巩 固 练 习
6×6×6=216(dm )
3×3×6=54(m )
返回目录
随 堂 练 习
1.教材第24页“做一做”。
0.75×0.5+0.75×1.6×2+0.5×1.6×2
=4.375(m2)
亮亮家要给一个长0.75m,宽0.5m,高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75m
0.5m
1.6m
=0.375+1.6+2.4
答:至少需要用布4.375m2。
2.教材第25页练习六第1题。
a
b
c
1.在展开图上找出相对的面,并用上、下、前、后、左、右标出,再用a、b、c标出每条棱。
上
下
前
左
后
右
a
a
b
b
b
b
c
c
c
c
c
c
2.教材第25页练习六第2题。
周四
周末
周五
2.将这个展开图围成正方体后,哪两个面分别相对?
周一对
周二对
周三对
2.教材第25页练习六第3题。
(1)计算各长方体中正面的面积。
(2)计算各长方体中右侧面的面积。
(3)计算各长方体中上面的面积。
4×2
=8(cm2)
3×3
=9(cm2)
2×2.5
=5(cm2)
2×3
=6(cm2)
2×3
=6(cm2)
2×2.5
=5(cm2)
3×4
=12(cm2)
2×3
=6(cm2)
2×2
=4(cm2)
3.教材第26页练习六第8题。
3×3×5
一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (鱼缸的上面没有盖。)
答:制作这个鱼缸时至少需要玻璃45dm2。
= 45(dm2)
返回目录
3.教材第26页练习六第10题。
50÷2
50×25+50×2.5×2+25×2.5×2
10.一个新建的游泳池长50m,长是宽的2倍,深2.5m,现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米的瓷砖?
=25(m)
= 1625(m2)
答:一共需要贴1625平方米的瓷砖。
课 堂 小 结
返回目录
2.在解决实际问题时,要认真读题,弄清楚要求长方体或正方体的哪几个面的面积。
正方体的表面积=棱长×棱长×6
正方体的表面积=棱长 ×6
长方体的表面积=(长×宽+长×高+高×宽)×2
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
1.计算长方体和正方体的表面积的不同方法。
作业1
作业2
返回目录
让我仔细想一想!
作 业 设 计
作业1
1.教材第25页练习六第4题。
(50×40+50×78+40×78)×2
=18040(cm2)
4.光华街口装了一个新的长方体铁皮邮箱,长50cm,宽40cm,高78cm,做这个邮箱至少需要贴多少平方厘米的铁皮?
答:做这个邮箱至少需要贴18040平方厘米的铁皮。
1.教材第25页练习六第5题。
(10×12+6×12)×2
=384(cm2)
5.一个长方体的饼干盒,长10cm,宽6cm,高12cm,如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有平方厘米?
答:这张商标纸的面积至少有384平方厘米。
返回作业设计
2.教材第26页练习六第9题。
1.2×1.2×6
=8.64(dm2)
8.64×1.5
=12.96(dm2)
9.一个正方体礼品盒,棱长1.2dm,如果包装这个礼品盒的用纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
答:至少要用12.96平方分米的包装纸。
基础巩固
提升培优
思维创新
作业2
返回作业设计
基础巩固
1.(重点题)计算下面立体图形的表面积。(单位:米)
(8×7+8×4+7×4)×2
5×5×6
(1)
(2)
8
7
4
5
5
5
= 232(平方米)
= 150(平方米)
基础巩固
2.(难点题)将一个长50cm、宽40cm、高35cm
的工具箱表面涂上漆,需要涂油漆的面积是多少?
(50×40+50×35+40×35)×2
答:需要涂油漆的面积是10300 。
= 10300( )
C㎡
C㎡
基础巩固
3.(难点题)有一个正方体收纳箱,棱长是0.8米,制作一个这样的收纳箱需要多少平方米木板?(该收纳箱无盖)
0.8×0.8×5
答:制作一个这样的收纳箱需要3.2平方米木板。
= 3.2(平方米)
返回作业2
基础巩固
4.(易错题)一间长12米,宽8米,高3米的教室,门窗面积为12平方米,现在四面墙壁及棚顶需要涂上涂料,如果每平方米要付涂料费2.8元钱,那么一共需要付涂料费多少钱?
12×8+12×3×2+8×3×2-12
答:一共需要付涂料费571.2元。
= 216-12
= 204(平方米)
204×2.8
= 571.2(元)
提升培优
5.(探究题)有一个正方体木块,把它分成3个大小相同的长方体之后,表面积增加了16㎡,这个木块原来的表面积是多少平方米?
答:这个木块原来的表面积是24㎡ 。
16÷4
= 4(㎡)
4×6
= 24(㎡)
返回作业2
提升培优
6.(操作题)一本书长20 ㎝,宽13 ㎝,厚0.6 ㎝,现有3本同样的书,将它们堆成一个长方体,使它的表面积最少,应该怎样放?
把面积最大的面叠放在一起。
思维创新
返回作业2
7.(竞赛题)如下图所示的立体图形由9个棱长为1厘米的小正方体搭成,这个立体图形的表面积为( )。
32平方厘米
5+5+6+6+5+5=32(个)
1×1×32=32(平方厘米)
返回目录
第3单元 长方体和正方体
五年级数学·下 新课标[人]
2 长方体和正方体的表面积
学习新知
随堂练习
作业设计
复习准备
复 习 准 备
返回目录
6cm
5cm
4cm
这个长方体:上、下两个面的长是( )cm,宽是( )cm。
前、后两个面的长是( )cm,宽是( )cm。
左、右两个面的长是( )cm,宽是( )cm。
6
5
6
4
5
4
学 习 新 知
物体表面的大小叫做物体的面积。
什么叫面积?
请你们拿出包装盒,沿着棱剪开,看看长方体和正方体的纸盒展开是什么形状。
小组里展示自己的展开图
在展开图中,分别用“上”“下”“前”
“后”“左”“右”标明6个面。
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
请在上面的展开图中,分别用“上”“下”
“前”“后”左”“右”标明6个面。
下
后
上
前
左
右
下
后
上
前
左
右
每个面的长和宽与长方体的长、宽、高有什么关系?
左面和右面
前、后两个面的长和宽分别是长方体的长和高,
下
后
上
前
左
右
观察长方体展开图,哪些面的面积相等?
上面和下面
前面和后面
上、下两个面的长和宽分别是长方体的长和宽,
左、右两个面的长和宽分别是长方体的宽和高。
折叠后,哪些图形能围成正方体?在括号中画“√”。
( )
练 习
( )
( )
√
√
摸一摸展开图每个面的大小。
长方体或正方体6个面的总面积,叫做它的表面积。
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
例1
要解决的问题与什么知识有关
要解决的问题与求长方体的表面积有关。
你获得了哪些信息
题中要求什么
微波炉的包装箱是一个长方体。
这个长方体的长是0.7 m,宽是0.5 m,高是0.4 m。
要求包装箱需要的硬纸板是多少平方米。
0.7m
0.5m
0.4m
前、后每个面,长______,宽_______,面积是__________;
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
例1
左、右每个面,长______,宽_______,面积是__________。
0.7m
0.5m
0.4m
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
这个包装箱的表面积是:
方法一:
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
= 0.7+0.56+0.4
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
例1
0.7m
0.5m
0.4m
做一个微波炉的包装箱,至少要用多少平方米的硬纸板?
这个包装箱的表面积是:
方法二:
(0.7×0.5+0.7×0.4+0.5×0.4)×2
= 0.83×2
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
例1
0.7m
0.5m
0.4m
长方体的表面积=(长×宽+长×高+高×宽)×2
(0.7×0.5+0.7×0.4+0.5×0.4)×2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
比较两种方法有什么不同,他们之间有什么联系?
上
和下
前
和后
右
和左
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
上(或下)
前(或后)
右(或左)
长方体的表面积=(长×宽+长×高+高×宽)×2
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
求出下图的表面积。
巩 固 练 习
解法1:
解法2:
解法3:
1.2×1.2×2+1.2×1×2+1.2×1×2
1.2×1.2×2+1.2×1×4=7.68(㎡)
(1.2×1.2+1.2×1+1.2×1)×2=7.68(㎡)
=2.88+2.4+2.4
=7.68(㎡)
6.5×6.5×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
6.5×6.5×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
写法一
6.5 ×6
= 42.25×6
=253.5(㎝ )
一个正方体墨水盒,棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板?
例2
求至少用多少平方厘米的硬纸板,就是求什么?
就是求正方体的表面积
答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。
写法二
小 结
正方体的表面积=棱长×棱长×6
正方体的表面积=棱长 ×6
求出各图的表面积。
巩 固 练 习
6×6×6=216(dm )
3×3×6=54(m )
返回目录
随 堂 练 习
1.教材第24页“做一做”。
0.75×0.5+0.75×1.6×2+0.5×1.6×2
=4.375(m2)
亮亮家要给一个长0.75m,宽0.5m,高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75m
0.5m
1.6m
=0.375+1.6+2.4
答:至少需要用布4.375m2。
2.教材第25页练习六第1题。
a
b
c
1.在展开图上找出相对的面,并用上、下、前、后、左、右标出,再用a、b、c标出每条棱。
上
下
前
左
后
右
a
a
b
b
b
b
c
c
c
c
c
c
2.教材第25页练习六第2题。
周四
周末
周五
2.将这个展开图围成正方体后,哪两个面分别相对?
周一对
周二对
周三对
2.教材第25页练习六第3题。
(1)计算各长方体中正面的面积。
(2)计算各长方体中右侧面的面积。
(3)计算各长方体中上面的面积。
4×2
=8(cm2)
3×3
=9(cm2)
2×2.5
=5(cm2)
2×3
=6(cm2)
2×3
=6(cm2)
2×2.5
=5(cm2)
3×4
=12(cm2)
2×3
=6(cm2)
2×2
=4(cm2)
3.教材第26页练习六第8题。
3×3×5
一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (鱼缸的上面没有盖。)
答:制作这个鱼缸时至少需要玻璃45dm2。
= 45(dm2)
返回目录
3.教材第26页练习六第10题。
50÷2
50×25+50×2.5×2+25×2.5×2
10.一个新建的游泳池长50m,长是宽的2倍,深2.5m,现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米的瓷砖?
=25(m)
= 1625(m2)
答:一共需要贴1625平方米的瓷砖。
课 堂 小 结
返回目录
2.在解决实际问题时,要认真读题,弄清楚要求长方体或正方体的哪几个面的面积。
正方体的表面积=棱长×棱长×6
正方体的表面积=棱长 ×6
长方体的表面积=(长×宽+长×高+高×宽)×2
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
1.计算长方体和正方体的表面积的不同方法。
作业1
作业2
返回目录
让我仔细想一想!
作 业 设 计
作业1
1.教材第25页练习六第4题。
(50×40+50×78+40×78)×2
=18040(cm2)
4.光华街口装了一个新的长方体铁皮邮箱,长50cm,宽40cm,高78cm,做这个邮箱至少需要贴多少平方厘米的铁皮?
答:做这个邮箱至少需要贴18040平方厘米的铁皮。
1.教材第25页练习六第5题。
(10×12+6×12)×2
=384(cm2)
5.一个长方体的饼干盒,长10cm,宽6cm,高12cm,如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有平方厘米?
答:这张商标纸的面积至少有384平方厘米。
返回作业设计
2.教材第26页练习六第9题。
1.2×1.2×6
=8.64(dm2)
8.64×1.5
=12.96(dm2)
9.一个正方体礼品盒,棱长1.2dm,如果包装这个礼品盒的用纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
答:至少要用12.96平方分米的包装纸。
基础巩固
提升培优
思维创新
作业2
返回作业设计
基础巩固
1.(重点题)计算下面立体图形的表面积。(单位:米)
(8×7+8×4+7×4)×2
5×5×6
(1)
(2)
8
7
4
5
5
5
= 232(平方米)
= 150(平方米)
基础巩固
2.(难点题)将一个长50cm、宽40cm、高35cm
的工具箱表面涂上漆,需要涂油漆的面积是多少?
(50×40+50×35+40×35)×2
答:需要涂油漆的面积是10300 。
= 10300( )
C㎡
C㎡
基础巩固
3.(难点题)有一个正方体收纳箱,棱长是0.8米,制作一个这样的收纳箱需要多少平方米木板?(该收纳箱无盖)
0.8×0.8×5
答:制作一个这样的收纳箱需要3.2平方米木板。
= 3.2(平方米)
返回作业2
基础巩固
4.(易错题)一间长12米,宽8米,高3米的教室,门窗面积为12平方米,现在四面墙壁及棚顶需要涂上涂料,如果每平方米要付涂料费2.8元钱,那么一共需要付涂料费多少钱?
12×8+12×3×2+8×3×2-12
答:一共需要付涂料费571.2元。
= 216-12
= 204(平方米)
204×2.8
= 571.2(元)
提升培优
5.(探究题)有一个正方体木块,把它分成3个大小相同的长方体之后,表面积增加了16㎡,这个木块原来的表面积是多少平方米?
答:这个木块原来的表面积是24㎡ 。
16÷4
= 4(㎡)
4×6
= 24(㎡)
返回作业2
提升培优
6.(操作题)一本书长20 ㎝,宽13 ㎝,厚0.6 ㎝,现有3本同样的书,将它们堆成一个长方体,使它的表面积最少,应该怎样放?
把面积最大的面叠放在一起。
思维创新
返回作业2
7.(竞赛题)如下图所示的立体图形由9个棱长为1厘米的小正方体搭成,这个立体图形的表面积为( )。
32平方厘米
5+5+6+6+5+5=32(个)
1×1×32=32(平方厘米)
返回目录
