2019中考数学压轴选择填空专题——新定义问题
文档属性
| 名称 | 2019中考数学压轴选择填空专题——新定义问题 |  | |
| 格式 | zip | ||
| 文件大小 | 327.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 07:20:30 | ||
图片预览



文档简介
新定义问题
例题精讲
例1.割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数 y=的图象与两坐标轴所围成的图形最接近的面积是( )
A.?5???????????????????????????????????????B.????????????????????????????????????????C.?4???????????????????????????????????????D.?17﹣4π
【答案】 A
【解析】【解答】解:如图,设抛物线与坐标轴的交点为A、B,则有:
A(4,0),B(0,4);
作直线l∥AB,易求得直线AB:y=﹣x+4,
所以设直线l:y=﹣x+h,当直线l与抛物线只有一个交点(相切)时,有:
﹣x+h=(x﹣4)2 ,
整理得:x2﹣x+4﹣h=0,
△=1﹣4×(4﹣h)=0,即h=3;
所以直线l:y=﹣x+3;
设直线l与坐标轴的交点为C、D,则C(3,0)、D(0,3),
因抛物线的图象与两坐标轴所围成的图形面积大于S△OCD小于S△OABS△OCD=×3×3=4.5. S△OAB=×4×4=8,
故抛物线的图象与两坐标轴所围成的图形面积在4.5<S<8的范围内,选项中符合的只有A,
故选A.
例2.定义一种对正整数n的“F”运算:
①当n为奇数时,结果为3n+5;
②当n为偶数时,结果为 (其中k是使 为奇数的正整数),并且运算重复进行.
例如,取n=26,那么当n=26时,第2016次“F运算”的结果是________.
【答案】 62
【解析】【解答】解:根据题意,得
当n=26时,第1次的计算结果是 =13,
第2次的计算结果是13×3+5=44,
第3次的计算结果是 =11,
第4次的计算结果是11×3+5=38,
第5次的计算结果是 =19,
第6次的计算结果是19×3+5=62,
第7次的计算结果是 =31,
第8次的计算结果是31×3+5=98,
第9次的计算结果是 =49,
第10次的计算结果是49×3+5=152,
第11次的计算结果是 =19,以下每6次运算一循环,
∵(2016﹣4)÷6=335…2,
∴第2016次“F运算”的结果与第6次的计算结果相同,为62,
故答案为:62.
例3.观察下列运算过程:S=1+3+32+33+…+32017+32018?? ①,
①×3得3S=3+32+33+…+32018+32019?? ②,
②﹣①得2S=32019﹣1,S= .
运用上面计算方法计算:1+5+52+53+…+52018=________.
【答案】
【解析】【解答】设S=1+5+52+53+…+52018 ①,
则5S=5+52+53+54…+52019②,
②﹣①得:4S=52019﹣1,所以S= ,
故答案为: .
例4.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= .现已知△ABC的三边长分别为1,2, ,则△ABC的面积为________.
【答案】1
【解析】【解答】解:∵S= ,
∴△ABC的三边长分别为1,2, ,则△ABC的面积为:
S= =1,
故答案为:1.
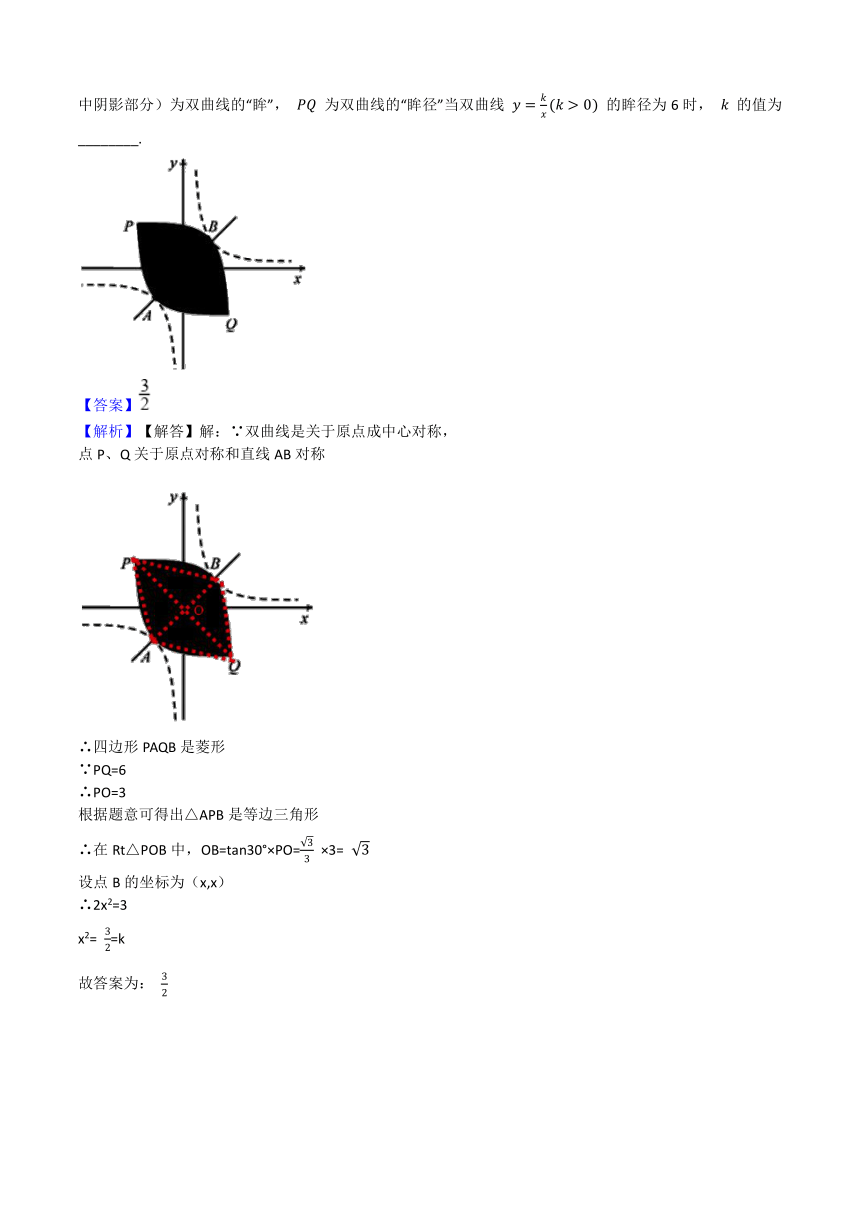
例5.设双曲线 与直线 交于 , 两点(点 在第三象限),将双曲线在第一象限的一支沿射线 的方向平移,使其经过点 ,将双曲线在第三象限的一支沿射线 的方向平移,使其经过点 ,平移后的两条曲线相交于点 , 两点,此时我称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”, 为双曲线的“眸径”当双曲线 的眸径为6时, 的值为________.
【答案】
【解析】【解答】解:∵双曲线是关于原点成中心对称,
点P、Q关于原点对称和直线AB对称
∴四边形PAQB是菱形
∵PQ=6
∴PO=3
根据题意可得出△APB是等边三角形
∴在Rt△POB中,OB=tan30°×PO= ×3=
设点B的坐标为(x,x)
∴2x2=3
x2= =k
故答案为:
习题练习
一、单选题
1.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(y,x).如f(2,3)=(3,2);
②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).
按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于(?? )
A.?(7,6)??????????????????????B.?(7,﹣6)??????????????????????C.?(﹣7,6)??????????????????????D.?(﹣7,﹣6)
2.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.?1??????????????????????????????????????D.?0
3.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是2(x+ );当矩形成为正方形时,就有x= (0>0),解得x=1,这时矩形的周长2(x+ )=4最小,因此x+ (x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是(?? )
A.?2???????????????????????????????????????????B.?1???????????????????????????????????????????C.?6???????????????????????????????????????????D.?10
4.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是(?? )
A.?1,2,3?????????????????????????B.?1,1, ?????????????????????????C.?1,1, ?????????????????????????D.?1,2,
5.在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②﹣①得6S﹣S=610﹣1,即5S=610﹣1,所以S= ,得出答案后,爱动脑筋的小林想:
如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是(?? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?a2014﹣1
6.阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为(?? )
A.?(60°,4)?????????????????B.?(45°,4)?????????????????C.?(60°,2 )?????????????????D.?(50°,2 )
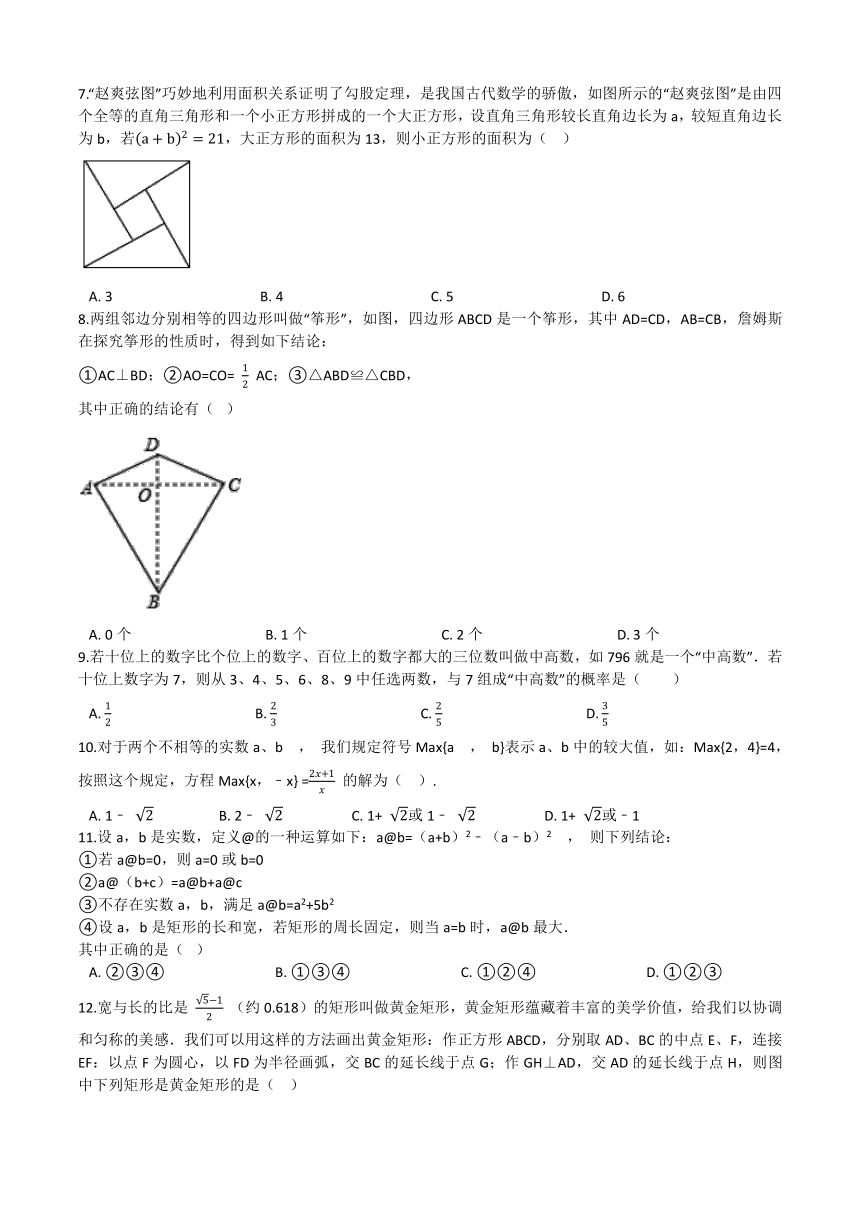
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为(?? )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
8.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,
其中正确的结论有(? )
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
9.若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.对于两个不相等的实数a、b , 我们规定符号Max{a , b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,﹣x} = 的解为(?? ).
A.?1﹣ ???????????????????B.?2﹣ ????????????????????C.?1+ 或1﹣ ????????????????????D.?1+ 或﹣1
11.设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:
①若a@b=0,则a=0或b=0
②a@(b+c)=a@b+a@c
③不存在实数a,b,满足a@b=a2+5b2
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是(? )
A.?②③④????????????????????????????????B.?①③④????????????????????????????????C.?①②④????????????????????????????????D.?①②③
12.宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是(?? )
A.?矩形ABFE?????????????????????????B.?矩形EFCD?????????????????????????C.?矩形EFGH?????????????????????????D.?矩形DCGH
13.对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,﹣1}=﹣1,若关于x的函数y=min{2x﹣1,﹣x+3},则该函数的最大值为(?? )
A.???????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
14.已知点A在函数(x>0)的图象上,点B在直线(k为常数,且k0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(???? )
A.?只有1对或2对???????????????????????B.?只有1对???????????????????????C.?只有2对???????????????????????D.?只有2对或3对
15.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是(?? )
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
16.定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]= x2的解为(?? )#N.
A.?0或 ??????????????????????????????B.?0或2??????????????????????????????C.?1或 ??????????????????????????????D.? 或﹣
二、填空题
17.对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n﹣ ≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;②(2x)=2(x);③若( )=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2013x)=m+(2013x);⑤(x+y)=(x)+(y);其中,正确的结论有________(填写所有正确的序号).
18.若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 =﹣1,﹣1的差倒数为 ,现已知x1=﹣ ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则 x2017=________.
19.在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
(1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(l1)、P(l2)都是过点P的△ABC的相似线(其中l1⊥BC,l2∥AC),此外,还有________条;
(2)如图②,∠C=90°,∠B=30°,当=________时,P(lx)截得的三角形面积为△ABC面积的 .
20.规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号) ①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
21.阅读理解:如图1,⊙O与直线a、b都相切,不论⊙O如何转动,直线a、b之间的距离始终保持不变(等于⊙O的直径),我们把具有这一特性的图形成为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力既可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线c,d之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线c,d之间的距离等于2cm,则莱洛三角形的周长为________cm.
22.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形 △CBD和△ABC相似,∠A =46°,则 ∠ACB的度数为________.
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】解:∵f(﹣6,7)=(7,﹣6),
∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6).
故选C.
2.【答案】 A
【解析】【解答】解:在同一坐标系xOy中,画出函数二次函数y=﹣x2+1与正比例函数y=﹣x的图象,如图所示.设它们交于点A、B.
令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x= 或 ,
∴A( , ),B( , ).
观察图象可知:
①???? 当x≤ 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为 ;
②当 <x< 时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为 ;
③当x≥ 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为 .
综上所示,min{﹣x2+1,﹣x}的最大值是 .
故选:A.
3.【答案】C
【解析】【解答】解:∵x>0,
∴在原式中分母分子同除以x,
即 =x+ ,
在面积是9的矩形中设矩形的一边长为x,则另一边长是 ,
矩形的周长是2(x+ );
当矩形成为正方形时,就有x= ,(x>0),
解得x=3,
这时矩形的周长2(x+ )=12最小,
因此x+ (x>0)的最小值是6.
故答案为:C
4.【答案】D
【解析】【解答】解:A、∵1+2=3,不能构成三角形,故选项错误; B、∵12+12=( )2 , 是等腰直角三角形,故选项错误;
C、底边上的高是 = ,可知是顶角120°,底角30°的等腰三角形,故选项错误;
D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,其中90°÷30°=3,符合“智慧三角形”的定义,故选项正确.
故选:D.
5.【答案】B
【解析】【解答】解:设S=1+a+a2+a3+a4+…+a2014 , ①
则aS=a+a2+a3+a4+…+a2014+a2015 , ②,
②﹣①得:(a﹣1)S=a2015﹣1,
∴S= ,
即1+a+a2+a3+a4+…+a2014= .
故答案为:B.
6.【答案】 A
【解析】【解答】解:如图,设正六边形的中心为D,连接AD,
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(60°,4).
故选:A.
7.【答案】 C
【解析】【解答】如图所示,∵ ,∴ =21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故答案为:C.
8.【答案】 D
【解析】【解答】解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
故③正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故①②正确;
故选D
9.【答案】 C
【解析】【解答】解:列表得:
9 379 479 579 679 879 ﹣
8 378 478 578 678 ﹣ 978
6 376 476 576 ﹣ 876 976
5 375 475 ﹣ 675 875 975
4 374 ﹣ 574 674 874 974
3 ﹣ 473 573 673 873 973
3 4 5 6 8 9
∵共有30种等可能的结果,与7组成“中高数”的有12种情况,
∴与7组成“中高数”的概率是:= .
故选C.
10.【答案】 D
【解析】【分析】根据x与﹣x的大小关系,取x与﹣x中的最大值化简所求方程,求出解即可.
【解答】当x<﹣x , 即x<0时,所求方程变形得:﹣x= ,
去分母得:x2+2x+1=0,即x=﹣1;
当x>﹣x , 即x>0时,所求方程变形得:x= ,即x2﹣2x=1,
解得:x=1+ 或x=1﹣ (舍去),
经检验x=﹣1与x=1+ 都为分式方程的解.
故选:D.
11.【答案】C
【解析】【解答】解:①根据题意得:a@b=(a+b)2﹣(a﹣b)2
∴(a+b)2﹣(a﹣b)2=0,
整理得:(a+b+a﹣b)(a+b﹣a+b)=0,即4ab=0,
解得:a=0或b=0,正确;
②∵a@(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4ab+4ac
a@b+a@c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
∴a@(b+c)=a@b+a@c正确;
③a@b=a2+5b2 , a@b=(a+b)2﹣(a﹣b)2 ,
令a2+5b2=(a+b)2﹣(a﹣b)2 ,
解得,a=0,b=0,故错误;
④∵a@b=(a+b)2﹣(a﹣b)2=4ab,
(a﹣b)2≥0,则a2﹣2ab+b2≥0,即a2+b2≥2ab,
∴a2+b2+2ab≥4ab,
∴4ab的最大值是a2+b2+2ab,此时a2+b2+2ab=4ab,
解得,a=b,
∴a@b最大时,a=b,故④正确,
故选C.
12.【答案】D
【解析】【解答】解:设正方形的边长为2,则CD=2,CF=1 在直角三角形DCF中,DF= =
∴FG=
∴CG= ﹣1
∴ =
∴矩形DCGH为黄金矩形
故选D.
13.【答案】 D
【解析】【解答】解:由题意得: ,解得: ,
当2x﹣1≥﹣x+3时,x≥ ,
∴当x≥ 时,y=min{2x﹣1,﹣x+3}=﹣x+3,
由图象可知:此时该函数的最大值为 ;
当2x﹣1<﹣x+3时,x< ,
∴当x< 时,y=min{2x﹣1,﹣x+3}=2x﹣1,
由图象可知:此时该函数的最大值为 ;
综上所述,y=min{2x﹣1,﹣x+3}的最大值是当x= 所对应的y的值,
如图所示,当x= 时,y= ,
故答案为:D.
14.【答案】 A
【解析】【解答】解:设A(a,),根据题意点A关于坐标原点对称的点B(-a,? )在直线y 2 = k x + 1 + k上,
∴=-ak+1+k,整理得:ka2-(k+1)a+1=0 ①,
即(a-1)(ka-1)=0,
∴a-1=0或ka-1=0,
则a=1或ka-1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a= , 此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上所述,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
15.【答案】 B
【解析】【解答】解:如图1,连接AC,CF,则AF=3 ,
∴两次变换相当于向右移动3格,向上移动3格,
又∵MN=20 ,
∴20 ÷3 ?= ,(不是整数)
∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,
此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是14次,
故选:B.
16.【答案】 A
【解析】【解答】解:当1≤x<2时, x2=1,解得x1= ,x2=﹣ ;
当x=0, x2=0,x=0;
当﹣1≤x<0时, x2=﹣1,方程没有实数解;
当﹣2≤x<﹣1时, x2=﹣1,方程没有实数解;
所以方程[x]= x2的解为0或 .
二、填空题
17.【答案】 ①③④
【解析】【解答】解:①(1.493)=1,正确;
②(2x)≠2(x),例如当x=0.3时,(2x)=1,2(x)=0,故②错误;
③若( )=4,则4﹣ ≤ x﹣1<4+ ,解得:9≤x<11,故③正确;
④m为整数,故(m+2013x)=m+(2013x),故④正确;
⑤(x+y)≠(x)+(y),例如x=0.3,y=0.4时,(x+y)=1,(x)+(y)=0,故⑤错误;
综上可得①③正确.
故答案为:①③④
18.【答案】
【解析】【解答】解:由题意可得,
x1=﹣ ,
x2= ,
x3= ,
x4= ,
2017÷3=672…1,
∴x2017= ,
故答案为: .
19.【答案】 1
;或或
【解析】【解答】(1)存在另外 1 条相似线.
如图1所示,过点P作l3∥BC交AC于Q,则△APQ∽△ABC;
故答案为:1;
(2)设P(lx)截得的三角形面积为S,S=S△ABC , 则相似比为1:2.
如图2所示,共有4条相似线:
①第1条l1 , 此时P为斜边AB中点,l1∥AC,∴=;
②第2条l2 , 此时P为斜边AB中点,l2∥BC,∴=;
③第3条l3 , 此时BP与BC为对应边,且=, ∴==;
④第4条l4 , 此时AP与AC为对应边,且=, ∴==, ∴=.
故答案为:或或.
20.【答案】②③
【解析】【解答】解:①当x=1.7时, [x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x= ;x+1=4x时,得x= ;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
21.【答案】2π
【解析】【解答】解:如图3,由题意知AB=BC=AC=2cm,
∴∠BAC=∠ABC=∠ACB=60°,
∴ 在以点C为圆心、2为半径的圆上,
∴ 的长为 = ,
则莱洛三角形的周长为 ×3=2π,
故答案为:2π.
22.【答案】113°或92°.
【解析】【解答】∵BCDBAC,
∴∠BCD=∠A=46°,
∵ACD为等腰三角形,∠ADC>∠BCD,
∴∠ADC>∠A,
∴ACCD,
①当AC=AD时,∠ACD=∠ADC=(180°-46°)=67°,
∴∠ACB=67°+46°=113°.
②当DA=DC时,∠ACD=∠A=46°,
例题精讲
例1.割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数 y=的图象与两坐标轴所围成的图形最接近的面积是( )
A.?5???????????????????????????????????????B.????????????????????????????????????????C.?4???????????????????????????????????????D.?17﹣4π
【答案】 A
【解析】【解答】解:如图,设抛物线与坐标轴的交点为A、B,则有:
A(4,0),B(0,4);
作直线l∥AB,易求得直线AB:y=﹣x+4,
所以设直线l:y=﹣x+h,当直线l与抛物线只有一个交点(相切)时,有:
﹣x+h=(x﹣4)2 ,
整理得:x2﹣x+4﹣h=0,
△=1﹣4×(4﹣h)=0,即h=3;
所以直线l:y=﹣x+3;
设直线l与坐标轴的交点为C、D,则C(3,0)、D(0,3),
因抛物线的图象与两坐标轴所围成的图形面积大于S△OCD小于S△OABS△OCD=×3×3=4.5. S△OAB=×4×4=8,
故抛物线的图象与两坐标轴所围成的图形面积在4.5<S<8的范围内,选项中符合的只有A,
故选A.
例2.定义一种对正整数n的“F”运算:
①当n为奇数时,结果为3n+5;
②当n为偶数时,结果为 (其中k是使 为奇数的正整数),并且运算重复进行.
例如,取n=26,那么当n=26时,第2016次“F运算”的结果是________.
【答案】 62
【解析】【解答】解:根据题意,得
当n=26时,第1次的计算结果是 =13,
第2次的计算结果是13×3+5=44,
第3次的计算结果是 =11,
第4次的计算结果是11×3+5=38,
第5次的计算结果是 =19,
第6次的计算结果是19×3+5=62,
第7次的计算结果是 =31,
第8次的计算结果是31×3+5=98,
第9次的计算结果是 =49,
第10次的计算结果是49×3+5=152,
第11次的计算结果是 =19,以下每6次运算一循环,
∵(2016﹣4)÷6=335…2,
∴第2016次“F运算”的结果与第6次的计算结果相同,为62,
故答案为:62.
例3.观察下列运算过程:S=1+3+32+33+…+32017+32018?? ①,
①×3得3S=3+32+33+…+32018+32019?? ②,
②﹣①得2S=32019﹣1,S= .
运用上面计算方法计算:1+5+52+53+…+52018=________.
【答案】
【解析】【解答】设S=1+5+52+53+…+52018 ①,
则5S=5+52+53+54…+52019②,
②﹣①得:4S=52019﹣1,所以S= ,
故答案为: .
例4.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= .现已知△ABC的三边长分别为1,2, ,则△ABC的面积为________.
【答案】1
【解析】【解答】解:∵S= ,
∴△ABC的三边长分别为1,2, ,则△ABC的面积为:
S= =1,
故答案为:1.
例5.设双曲线 与直线 交于 , 两点(点 在第三象限),将双曲线在第一象限的一支沿射线 的方向平移,使其经过点 ,将双曲线在第三象限的一支沿射线 的方向平移,使其经过点 ,平移后的两条曲线相交于点 , 两点,此时我称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”, 为双曲线的“眸径”当双曲线 的眸径为6时, 的值为________.
【答案】
【解析】【解答】解:∵双曲线是关于原点成中心对称,
点P、Q关于原点对称和直线AB对称
∴四边形PAQB是菱形
∵PQ=6
∴PO=3
根据题意可得出△APB是等边三角形
∴在Rt△POB中,OB=tan30°×PO= ×3=
设点B的坐标为(x,x)
∴2x2=3
x2= =k
故答案为:
习题练习
一、单选题
1.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(y,x).如f(2,3)=(3,2);
②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).
按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于(?? )
A.?(7,6)??????????????????????B.?(7,﹣6)??????????????????????C.?(﹣7,6)??????????????????????D.?(﹣7,﹣6)
2.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.?1??????????????????????????????????????D.?0
3.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是2(x+ );当矩形成为正方形时,就有x= (0>0),解得x=1,这时矩形的周长2(x+ )=4最小,因此x+ (x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是(?? )
A.?2???????????????????????????????????????????B.?1???????????????????????????????????????????C.?6???????????????????????????????????????????D.?10
4.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是(?? )
A.?1,2,3?????????????????????????B.?1,1, ?????????????????????????C.?1,1, ?????????????????????????D.?1,2,
5.在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②﹣①得6S﹣S=610﹣1,即5S=610﹣1,所以S= ,得出答案后,爱动脑筋的小林想:
如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是(?? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?a2014﹣1
6.阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为(?? )
A.?(60°,4)?????????????????B.?(45°,4)?????????????????C.?(60°,2 )?????????????????D.?(50°,2 )
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为(?? )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
8.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,
其中正确的结论有(? )
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
9.若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.对于两个不相等的实数a、b , 我们规定符号Max{a , b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,﹣x} = 的解为(?? ).
A.?1﹣ ???????????????????B.?2﹣ ????????????????????C.?1+ 或1﹣ ????????????????????D.?1+ 或﹣1
11.设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:
①若a@b=0,则a=0或b=0
②a@(b+c)=a@b+a@c
③不存在实数a,b,满足a@b=a2+5b2
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是(? )
A.?②③④????????????????????????????????B.?①③④????????????????????????????????C.?①②④????????????????????????????????D.?①②③
12.宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是(?? )
A.?矩形ABFE?????????????????????????B.?矩形EFCD?????????????????????????C.?矩形EFGH?????????????????????????D.?矩形DCGH
13.对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,﹣1}=﹣1,若关于x的函数y=min{2x﹣1,﹣x+3},则该函数的最大值为(?? )
A.???????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
14.已知点A在函数(x>0)的图象上,点B在直线(k为常数,且k0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(???? )
A.?只有1对或2对???????????????????????B.?只有1对???????????????????????C.?只有2对???????????????????????D.?只有2对或3对
15.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是(?? )
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
16.定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]= x2的解为(?? )#N.
A.?0或 ??????????????????????????????B.?0或2??????????????????????????????C.?1或 ??????????????????????????????D.? 或﹣
二、填空题
17.对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n﹣ ≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;②(2x)=2(x);③若( )=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2013x)=m+(2013x);⑤(x+y)=(x)+(y);其中,正确的结论有________(填写所有正确的序号).
18.若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 =﹣1,﹣1的差倒数为 ,现已知x1=﹣ ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则 x2017=________.
19.在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
(1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(l1)、P(l2)都是过点P的△ABC的相似线(其中l1⊥BC,l2∥AC),此外,还有________条;
(2)如图②,∠C=90°,∠B=30°,当=________时,P(lx)截得的三角形面积为△ABC面积的 .
20.规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号) ①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
21.阅读理解:如图1,⊙O与直线a、b都相切,不论⊙O如何转动,直线a、b之间的距离始终保持不变(等于⊙O的直径),我们把具有这一特性的图形成为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力既可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线c,d之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线c,d之间的距离等于2cm,则莱洛三角形的周长为________cm.
22.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形 △CBD和△ABC相似,∠A =46°,则 ∠ACB的度数为________.
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】解:∵f(﹣6,7)=(7,﹣6),
∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6).
故选C.
2.【答案】 A
【解析】【解答】解:在同一坐标系xOy中,画出函数二次函数y=﹣x2+1与正比例函数y=﹣x的图象,如图所示.设它们交于点A、B.
令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x= 或 ,
∴A( , ),B( , ).
观察图象可知:
①???? 当x≤ 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为 ;
②当 <x< 时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为 ;
③当x≥ 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为 .
综上所示,min{﹣x2+1,﹣x}的最大值是 .
故选:A.
3.【答案】C
【解析】【解答】解:∵x>0,
∴在原式中分母分子同除以x,
即 =x+ ,
在面积是9的矩形中设矩形的一边长为x,则另一边长是 ,
矩形的周长是2(x+ );
当矩形成为正方形时,就有x= ,(x>0),
解得x=3,
这时矩形的周长2(x+ )=12最小,
因此x+ (x>0)的最小值是6.
故答案为:C
4.【答案】D
【解析】【解答】解:A、∵1+2=3,不能构成三角形,故选项错误; B、∵12+12=( )2 , 是等腰直角三角形,故选项错误;
C、底边上的高是 = ,可知是顶角120°,底角30°的等腰三角形,故选项错误;
D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,其中90°÷30°=3,符合“智慧三角形”的定义,故选项正确.
故选:D.
5.【答案】B
【解析】【解答】解:设S=1+a+a2+a3+a4+…+a2014 , ①
则aS=a+a2+a3+a4+…+a2014+a2015 , ②,
②﹣①得:(a﹣1)S=a2015﹣1,
∴S= ,
即1+a+a2+a3+a4+…+a2014= .
故答案为:B.
6.【答案】 A
【解析】【解答】解:如图,设正六边形的中心为D,连接AD,
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(60°,4).
故选:A.
7.【答案】 C
【解析】【解答】如图所示,∵ ,∴ =21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故答案为:C.
8.【答案】 D
【解析】【解答】解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
故③正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故①②正确;
故选D
9.【答案】 C
【解析】【解答】解:列表得:
9 379 479 579 679 879 ﹣
8 378 478 578 678 ﹣ 978
6 376 476 576 ﹣ 876 976
5 375 475 ﹣ 675 875 975
4 374 ﹣ 574 674 874 974
3 ﹣ 473 573 673 873 973
3 4 5 6 8 9
∵共有30种等可能的结果,与7组成“中高数”的有12种情况,
∴与7组成“中高数”的概率是:= .
故选C.
10.【答案】 D
【解析】【分析】根据x与﹣x的大小关系,取x与﹣x中的最大值化简所求方程,求出解即可.
【解答】当x<﹣x , 即x<0时,所求方程变形得:﹣x= ,
去分母得:x2+2x+1=0,即x=﹣1;
当x>﹣x , 即x>0时,所求方程变形得:x= ,即x2﹣2x=1,
解得:x=1+ 或x=1﹣ (舍去),
经检验x=﹣1与x=1+ 都为分式方程的解.
故选:D.
11.【答案】C
【解析】【解答】解:①根据题意得:a@b=(a+b)2﹣(a﹣b)2
∴(a+b)2﹣(a﹣b)2=0,
整理得:(a+b+a﹣b)(a+b﹣a+b)=0,即4ab=0,
解得:a=0或b=0,正确;
②∵a@(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4ab+4ac
a@b+a@c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
∴a@(b+c)=a@b+a@c正确;
③a@b=a2+5b2 , a@b=(a+b)2﹣(a﹣b)2 ,
令a2+5b2=(a+b)2﹣(a﹣b)2 ,
解得,a=0,b=0,故错误;
④∵a@b=(a+b)2﹣(a﹣b)2=4ab,
(a﹣b)2≥0,则a2﹣2ab+b2≥0,即a2+b2≥2ab,
∴a2+b2+2ab≥4ab,
∴4ab的最大值是a2+b2+2ab,此时a2+b2+2ab=4ab,
解得,a=b,
∴a@b最大时,a=b,故④正确,
故选C.
12.【答案】D
【解析】【解答】解:设正方形的边长为2,则CD=2,CF=1 在直角三角形DCF中,DF= =
∴FG=
∴CG= ﹣1
∴ =
∴矩形DCGH为黄金矩形
故选D.
13.【答案】 D
【解析】【解答】解:由题意得: ,解得: ,
当2x﹣1≥﹣x+3时,x≥ ,
∴当x≥ 时,y=min{2x﹣1,﹣x+3}=﹣x+3,
由图象可知:此时该函数的最大值为 ;
当2x﹣1<﹣x+3时,x< ,
∴当x< 时,y=min{2x﹣1,﹣x+3}=2x﹣1,
由图象可知:此时该函数的最大值为 ;
综上所述,y=min{2x﹣1,﹣x+3}的最大值是当x= 所对应的y的值,
如图所示,当x= 时,y= ,
故答案为:D.
14.【答案】 A
【解析】【解答】解:设A(a,),根据题意点A关于坐标原点对称的点B(-a,? )在直线y 2 = k x + 1 + k上,
∴=-ak+1+k,整理得:ka2-(k+1)a+1=0 ①,
即(a-1)(ka-1)=0,
∴a-1=0或ka-1=0,
则a=1或ka-1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a= , 此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上所述,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
15.【答案】 B
【解析】【解答】解:如图1,连接AC,CF,则AF=3 ,
∴两次变换相当于向右移动3格,向上移动3格,
又∵MN=20 ,
∴20 ÷3 ?= ,(不是整数)
∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,
此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是14次,
故选:B.
16.【答案】 A
【解析】【解答】解:当1≤x<2时, x2=1,解得x1= ,x2=﹣ ;
当x=0, x2=0,x=0;
当﹣1≤x<0时, x2=﹣1,方程没有实数解;
当﹣2≤x<﹣1时, x2=﹣1,方程没有实数解;
所以方程[x]= x2的解为0或 .
二、填空题
17.【答案】 ①③④
【解析】【解答】解:①(1.493)=1,正确;
②(2x)≠2(x),例如当x=0.3时,(2x)=1,2(x)=0,故②错误;
③若( )=4,则4﹣ ≤ x﹣1<4+ ,解得:9≤x<11,故③正确;
④m为整数,故(m+2013x)=m+(2013x),故④正确;
⑤(x+y)≠(x)+(y),例如x=0.3,y=0.4时,(x+y)=1,(x)+(y)=0,故⑤错误;
综上可得①③正确.
故答案为:①③④
18.【答案】
【解析】【解答】解:由题意可得,
x1=﹣ ,
x2= ,
x3= ,
x4= ,
2017÷3=672…1,
∴x2017= ,
故答案为: .
19.【答案】 1
;或或
【解析】【解答】(1)存在另外 1 条相似线.
如图1所示,过点P作l3∥BC交AC于Q,则△APQ∽△ABC;
故答案为:1;
(2)设P(lx)截得的三角形面积为S,S=S△ABC , 则相似比为1:2.
如图2所示,共有4条相似线:
①第1条l1 , 此时P为斜边AB中点,l1∥AC,∴=;
②第2条l2 , 此时P为斜边AB中点,l2∥BC,∴=;
③第3条l3 , 此时BP与BC为对应边,且=, ∴==;
④第4条l4 , 此时AP与AC为对应边,且=, ∴==, ∴=.
故答案为:或或.
20.【答案】②③
【解析】【解答】解:①当x=1.7时, [x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x= ;x+1=4x时,得x= ;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
21.【答案】2π
【解析】【解答】解:如图3,由题意知AB=BC=AC=2cm,
∴∠BAC=∠ABC=∠ACB=60°,
∴ 在以点C为圆心、2为半径的圆上,
∴ 的长为 = ,
则莱洛三角形的周长为 ×3=2π,
故答案为:2π.
22.【答案】113°或92°.
【解析】【解答】∵BCDBAC,
∴∠BCD=∠A=46°,
∵ACD为等腰三角形,∠ADC>∠BCD,
∴∠ADC>∠A,
∴ACCD,
①当AC=AD时,∠ACD=∠ADC=(180°-46°)=67°,
∴∠ACB=67°+46°=113°.
②当DA=DC时,∠ACD=∠A=46°,
同课章节目录
