人教高中数学选修1-1第一章 1.3简单逻辑连接词或且非优质课课件共23张PPT
文档属性
| 名称 | 人教高中数学选修1-1第一章 1.3简单逻辑连接词或且非优质课课件共23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 642.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 15:23:15 | ||
图片预览








文档简介
课件23张PPT。1.3简单逻辑连接词一个明智的人总是抓住机遇,把它变成美好的未来。同学们:加油!!!目标解读知识与技能:了解逻辑连接词“或”“且”“非”的含义,会用“且”“或”连接两个命题,能判断含有逻辑连接词“且”“或”命题的真假。
过程与方法:通过实例,领悟逻辑连接词“或”“且”“非”构成的命题形式,体会由特殊到一般的思想方法。
情感态度价值观:感悟数学语言的准确性、简洁性,激发学习数学的兴趣。 逻辑连接词
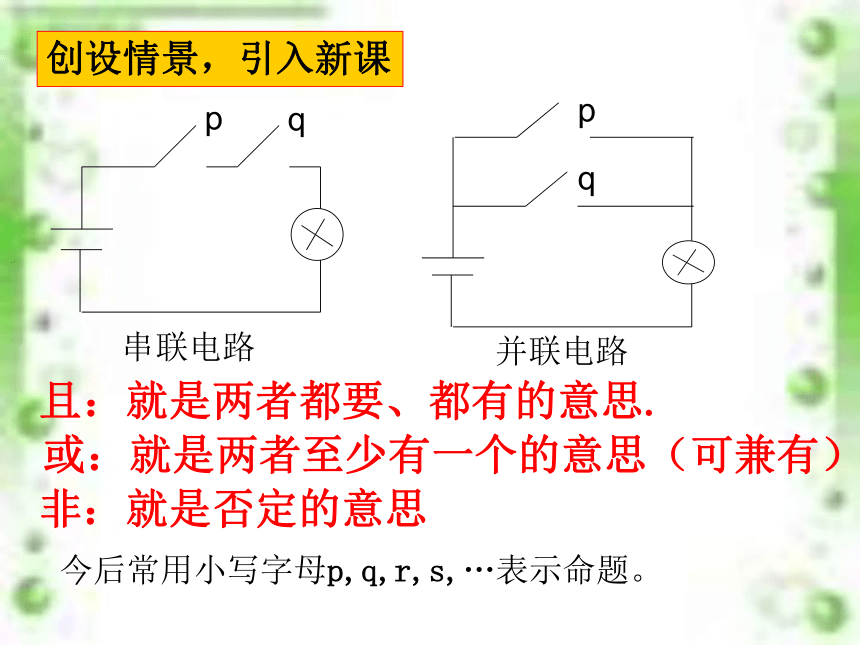
“或”“且”“非”创设情景,引入新课且:就是两者都要、都有的意思.或:就是两者至少有一个的意思(可兼有)非:就是否定的意思 今后常用小写字母p,q,r,s,…表示命题。 探究新知,巩固练习 下列命题中,命题间有什么关系? (1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除;1.问题1:命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题. 一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q” 2.问题2
思考:命题 p∧q的真假如何确定?
观察下列各组命题,命题p∧q的真假与p、q的真假有什么联系? P:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两边相等且三条中线相等. P:6是奇数;
q:6是素数;
p∧q:6是奇数且是素数.填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .一句话概括:
全真为真,有假即假. 真命题假命题命题p∧q的真假判断方法:假假假真探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思活动探究★★ 或 (or)下列命题中,命题 间有什么关系? (1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.1.问题1:命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题. 一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.思考:命题 p∨q的真假如何确定?
观察下列三组命题,命题p∨q的真假与p、q 的真假有什么联系? P:27是7的倍数;
q:27是9的倍数;
p∨q :27是7的倍数或是9的倍数.P:等腰梯形对角线垂直;
q:等腰梯形对角线平分;
p∨q:等腰梯形对角线垂直或平分.P:三边对应成比例的两个三角形相似;
q:三角对应相等的两个三角形相似;
p∨q:三边对应成比例或三角对应相等的两 个三角形相似. 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.一句话概括:
有真即真, 全假为假. 一真假命题p∨q的真假判断方法:假真真真下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根★★ 非 (not) 一般地,对一个命题p全盘否定,就得到一个新命题,记作? p,读作“非p”或“p的否定”.命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.1.问题1填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?一句话概括:
真假相反p与┐p真假性相反真命题假命题 假真 对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?活动探究探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?命题的否定与否命题是完全不同的概念 (1)原命题“若P则q” 的形式,它的非命题“若p,则?q”;而它的否命题为 “若┓p,则┓q”.
(2)命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.命题的否定与否命题的区别例:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:正方形的四条边不相等.若一个四边形不是正方形,则它的四条边不相等.
例4:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.例题分析 一般地,对一个命题p全盘否定,就得到一个新命题,记作读作“非p”或“p的否定” 若p是真命题,则?p必是假命题;若p是假命题,则?p必是真命题.3、“非”(not)规定:
1.若p,q都是真命题时,
“p且q”是真命题;
若p,q两个命题中有一个是假命题时,
“ p且q”是假命题
2.若p,q两个命题中有一个是真命题时,
“p或q”是真命题;
若p,q两个命题都是假命题时,
“p或q”是假命题
3. 若p是真命题,则﹁p必是假命题;
若p是假命题,则﹁p必是真命题.一假必假一真则真真假相反逻辑联结词“或”“且”“非”的含义或:就是两者至少有一个的意思(可兼容)
且:就是两者都有的意思
非:就是否定的意思1.命题“方程x2=1的解是x=±1”,使用逻辑联结词的情况是 ( )
A.没有使用逻辑联结词 B.使用了逻辑联结词“或”
C.使用了逻辑联结词“且” D.使用了逻辑联结词“非”
2.已知p:2+2=5,q:3>2,则下列判断中,错误的是 ( )
A.p或q为真,非q为假 B.p且q为假,非p为真
C.p且q为假,非p为假 D.p且q为假,p或q为真BC 含有逻辑联结词“且”、“或”、“非”的命题称为复合命题课堂检测:(看谁最快)
3.若命题“﹁p”与命题“p∨q”都是真命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
B命题的否定须注意的几个方面:(1)“≥”的意义是“>或=”.(2)“非”命题对常见的几个正面词语的否定.祝同学们学习进步!
过程与方法:通过实例,领悟逻辑连接词“或”“且”“非”构成的命题形式,体会由特殊到一般的思想方法。
情感态度价值观:感悟数学语言的准确性、简洁性,激发学习数学的兴趣。 逻辑连接词
“或”“且”“非”创设情景,引入新课且:就是两者都要、都有的意思.或:就是两者至少有一个的意思(可兼有)非:就是否定的意思 今后常用小写字母p,q,r,s,…表示命题。 探究新知,巩固练习 下列命题中,命题间有什么关系? (1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除;1.问题1:命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题. 一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q” 2.问题2
思考:命题 p∧q的真假如何确定?
观察下列各组命题,命题p∧q的真假与p、q的真假有什么联系? P:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两边相等且三条中线相等. P:6是奇数;
q:6是素数;
p∧q:6是奇数且是素数.填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .一句话概括:
全真为真,有假即假. 真命题假命题命题p∧q的真假判断方法:假假假真探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思活动探究★★ 或 (or)下列命题中,命题 间有什么关系? (1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.1.问题1:命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题. 一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.思考:命题 p∨q的真假如何确定?
观察下列三组命题,命题p∨q的真假与p、q 的真假有什么联系? P:27是7的倍数;
q:27是9的倍数;
p∨q :27是7的倍数或是9的倍数.P:等腰梯形对角线垂直;
q:等腰梯形对角线平分;
p∨q:等腰梯形对角线垂直或平分.P:三边对应成比例的两个三角形相似;
q:三角对应相等的两个三角形相似;
p∨q:三边对应成比例或三角对应相等的两 个三角形相似. 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.一句话概括:
有真即真, 全假为假. 一真假命题p∨q的真假判断方法:假真真真下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根★★ 非 (not) 一般地,对一个命题p全盘否定,就得到一个新命题,记作? p,读作“非p”或“p的否定”.命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.1.问题1填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?一句话概括:
真假相反p与┐p真假性相反真命题假命题 假真 对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?活动探究探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?命题的否定与否命题是完全不同的概念 (1)原命题“若P则q” 的形式,它的非命题“若p,则?q”;而它的否命题为 “若┓p,则┓q”.
(2)命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.命题的否定与否命题的区别例:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:正方形的四条边不相等.若一个四边形不是正方形,则它的四条边不相等.
例4:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.例题分析 一般地,对一个命题p全盘否定,就得到一个新命题,记作读作“非p”或“p的否定” 若p是真命题,则?p必是假命题;若p是假命题,则?p必是真命题.3、“非”(not)规定:
1.若p,q都是真命题时,
“p且q”是真命题;
若p,q两个命题中有一个是假命题时,
“ p且q”是假命题
2.若p,q两个命题中有一个是真命题时,
“p或q”是真命题;
若p,q两个命题都是假命题时,
“p或q”是假命题
3. 若p是真命题,则﹁p必是假命题;
若p是假命题,则﹁p必是真命题.一假必假一真则真真假相反逻辑联结词“或”“且”“非”的含义或:就是两者至少有一个的意思(可兼容)
且:就是两者都有的意思
非:就是否定的意思1.命题“方程x2=1的解是x=±1”,使用逻辑联结词的情况是 ( )
A.没有使用逻辑联结词 B.使用了逻辑联结词“或”
C.使用了逻辑联结词“且” D.使用了逻辑联结词“非”
2.已知p:2+2=5,q:3>2,则下列判断中,错误的是 ( )
A.p或q为真,非q为假 B.p且q为假,非p为真
C.p且q为假,非p为假 D.p且q为假,p或q为真BC 含有逻辑联结词“且”、“或”、“非”的命题称为复合命题课堂检测:(看谁最快)
3.若命题“﹁p”与命题“p∨q”都是真命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
B命题的否定须注意的几个方面:(1)“≥”的意义是“>或=”.(2)“非”命题对常见的几个正面词语的否定.祝同学们学习进步!
