2018-2019学年上海市虹口区高二(下)期中数学试卷解析版
文档属性
| 名称 | 2018-2019学年上海市虹口区高二(下)期中数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 15:16:23 | ||
图片预览




文档简介
2018-2019学年上海市虹口区高二(下)期中数学试卷
一、填空题(本大题共12题,每题3分,共36分)
1.(3分)过点(1,0)且与直线x﹣y=0平行的直线方程是 .
2.(3分)将边长分别为1cm和2cm的矩形,绕边长为2cm的一边所在的直线旋转一周得到一圆柱,则该圆柱的侧面积为 cm2.
3.(3分)以A(1,1),B(3,﹣1)为直径的端点的圆的方程是 .
4.(3分)正方体的外接球体积为V1,其内切球体积为V2,则的值为 .
5.(3分)椭圆的长轴长是短轴长的2倍,它的一个焦点为(,0),则椭圆的标准方程是 .
6.(3分)已知正四棱锥的底面边长是2,侧棱长是,则该正四棱锥的全面积为 .
7.(3分)双曲线﹣=1(a>0)的一条渐近线方程为y=2x,则a的值为 .
8.(3分)点P是棱长为a的正方体ABCD﹣A1B1C1D1棱A1B1上的动点,则四棱锥P﹣ABC1D1的体积为 .
9.(3分)已知椭圆+=1(m>0)和曲线﹣=1(n>0)有相同的焦点F1、F2,点P为椭圆和双曲线的一个交点,则|PF1|?|PF2|的值是 .
10.(3分)正方形铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径圆弧,剪下一个顶角为的扇形,用这块扇形铁片围成一个圆锥形容器,则这个圆锥形容器的容积等于 cm3.
11.(3分)在棱长为a的正方体ABCD﹣A1B1C1D1中,M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心,则过点M、N、P的平面截正方体的截面面积为 .
12.(3分)在平面直角坐标系xOy中,C为直线y=5上的动点,以C为圆心的圆C截y轴所得的弦长恒为6,过原点O作圆C的一条切线,切点为P,则点P到直线3x+4y﹣25=0的距离的最小值为 .
二、选择题(本大题共4题,每题3分,共12分)
13.(3分)直线m⊥平面α,下面判断错误的是( )
A.若直线n⊥m,则n∥α B.若直线n⊥α,则n∥m
C.若直线n∥α,则n⊥m D.若直线n∥m,则n⊥α
14.(3分)已知直线1:2x﹣y+2=0被双曲线C:x2﹣=1截得的线段长等于3,下面哪一条直线被双曲线C所截得的弦长不等于3( )
A.l:2y﹣x+2=0 B.l:﹣2x﹣y+2=0
C.l:2x+y+2=0 D.l:2x﹣y﹣2=0
15.(3分)有一把三角尺ABC,∠A=30°,∠C=90°,把边BC放置在桌面上,当三角尺与桌面所在的平面成60°的时候,AB边所在的直线与桌面所成的角等于( )
A.arcsin B. C. D.arcsin
16.(3分)阅读材料:空间直角坐标系O﹣xyz中,过点P(x0,y0,z0)且一个法向量为=(a,b,c)的平面α的方程为a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;过点P(x0,y0,z0)且个方向向量为=(u,v,w)(uvw≠0)的直线l的方程为==,阅读上面材料,并解决下面问题:已知平面α的方程为x+2y﹣2z﹣4=0,直线l是两平面3x﹣2y﹣7=0与2y﹣z+6=0的交线,则直线l与平面α所成角的大小为( )
A.arcsin B.arcsin
C.arcsin D.arcsin
三、解答题(本大题共4题,共52分,解答时写出必要的步骤)
17.(8分)抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
18.(8分)如图,AB是异面直线a、b的公垂线,长度为2,点C、D分别在直线a和b上,且CD长为4,过线段AB的中点M作平面α,使得AB⊥平面α,线段CD与平面α交点为N.
(1)求异面直线AB和CD所成的角的大小;
(2)求证:直线a∥α且CN=DN.
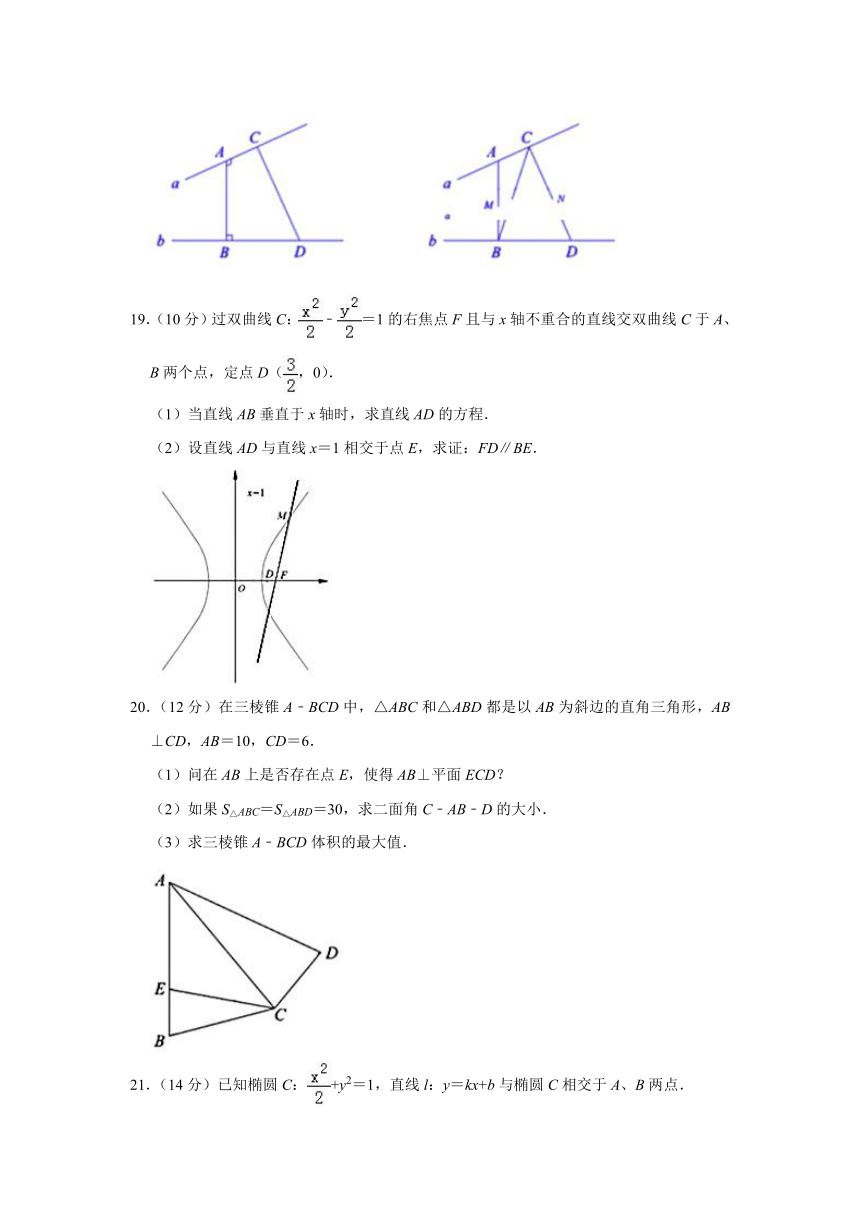
19.(10分)过双曲线C:﹣=1的右焦点F且与x轴不重合的直线交双曲线C于A、B两个点,定点D(,0).
(1)当直线AB垂直于x轴时,求直线AD的方程.
(2)设直线AD与直线x=1相交于点E,求证:FD∥BE.
20.(12分)在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,AB⊥CD,AB=10,CD=6.
(1)问在AB上是否存在点E,使得AB⊥平面ECD?
(2)如果S△ABC=S△ABD=30,求二面角C﹣AB﹣D的大小.
(3)求三棱锥A﹣BCD体积的最大值.
21.(14分)已知椭圆C:+y2=1,直线l:y=kx+b与椭圆C相交于A、B两点.
(1)如果k+b=﹣,求动直线l所过的定点;
(2)记椭圆C的上顶点为D,如果∠ADB=,证明动直线l过定点P(0,﹣);
(3)如果b=﹣,点B关于y轴的对称点为B',向直线AB'是过定点?如果是,求出定点的坐标;如果不是,请说明理由.
2018-2019学年上海市虹口区高二(下)期中数学试卷
参考答案与试题解析
一、填空题(本大题共12题,每题3分,共36分)
1.【解答】解:设与直线x﹣y=0平行的直线方程是x﹣y+m=0,
且直线过点(1,0),则1﹣0+m=0,解得m=﹣1,
所以所求直线方程是x﹣y﹣1=0.
故答案为:x﹣y﹣1=0.
2.【解答】
解:依题意,将该圆柱的侧面展开,则展开图是以2π为长,以2为宽的矩形,
所以该圆柱的侧面积为S=2π×2=4π.
故填:4π.
3.【解答】解:点A(1,1),B(3,﹣1),则AB的中点为M(2,0),
AB的长为|AB|==2,
所以以AB为直径的端点的圆的圆心为M,半径为,
所求圆的方程是(x﹣2)2+y2=2.
故答案为:(x﹣2)2+y2=2.
4.【解答】解:设正方体的棱长为2a,
则其外接球的半径为,
内切球的半径为a,
则,.
∴.
故答案为:.
5.【解答】解:依题意得2a=4b,c=,又a2=b2+c2,
∴a=1,b=1,
故答案为:+y2=1.
6.【解答】解:如图在正四棱锥S﹣ABCD中,O为底面正方形的中心,E为BC的中点,连接OE,SO,SE,
则SO⊥平面ABCD,又BC?平面ABCD,所以BC⊥SO,
在三角形ABC中,O,E分别为AC,BC的中点,所以OE∥AB,又因为AB⊥BC,所以BC⊥OE.
又OE∩SO=0,所以BC⊥平面SOE,因为SE?平面SOE,
所以SE⊥BC,即SE为侧面SBC的斜高,
三角形SBE为直角三角形,所以SE===2.
所以该正四棱锥的全面积S全=SABCD+4×SSBC=2×2+4×=4+8=12.
故填:12.
7.【解答】解:双曲线=1(a>0)的一条渐近线方程为y=2x,
可得:,解得a=1.
故答案为:1.
8.【解答】解:连接B1C交BC1于点O,显然OB1=B1C=BC1=a,
∵四边形BCC1B1是正方形,∴BC1⊥B1C,
∵AB⊥平面BCC1B1,∴AB⊥B1O,
又AB∩BC1=B,
∴OB1⊥平面ABC1D1,
∵A1B1∥AB,∴A1B1∥平面ABC1D1,
∴P到平面ABC1D1的距离等于B1O,
∴V===.
故答案为:.
9.【解答】解:∵已知椭圆+=1(m>0)和曲线﹣=1(n>0)有相同的焦点F1、F2,
∴m2﹣9=n2+4,即m2﹣n2=13,
假设P在第一象限,根据椭圆和双曲线的定义可得:|PF1|+|PF2|=2m,|PF1|﹣|PF2|=2n,
两式平方差得4|PF1|?|PF2|=4m2﹣4n2=4×13,∴|PF1|?|PF2|=13.
故答案为13.
10.【解答】
解:依题意,设该圆锥的母线长为l,则l=4,
设底面圆的半径为r,则2πr==2π,解得r=1,
所以圆锥的高h==,
所以这个圆锥形容器的容积V=×πr2×h==π.
故填:.
11.【解答】解:依题意,M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心,即M,N,P分别为AB1、B1C、AC的中点,
所以过点M、N、P的平面截正方体的截面为三角形AB1C,如图.
因为正方体的棱长为a,所以三角形AB1C,的边长为a,所以三角形AB1C,的面积为:S==.
故填:.
12.【解答】解:根据题意,设C的坐标为(m,5),圆C的半径为r,
又由圆C截y轴所得的弦长恒为6,则点(0,2)在圆C上,则r2=m2+9,
又由过原点O作圆C的一条切线,切点为P,则|CP|2=r2=m2+9,
|OC|2=m2+25,
则|OP|2=|OC|2﹣|CP|2=(m2+25)﹣(m2+9)=16,
则P在以O为圆心,半径为4的圆上,
其圆心O到直线3x+4y﹣25=0的距离d==5,
则P到直线3x+4y﹣25=0的距离的最小值为d﹣r=5﹣4=1,
故答案为:1
二、选择题(本大题共4题,每题3分,共12分)
13.【解答】解:由直线m⊥平面α,得:
在A中,若直线n⊥m,则由线面平行性质得n与α相交、平行或n?α,故A错误;
在B中,若直线n⊥α,则由线面垂直的性质得n∥m,故B正确;
在C中,若直线n∥α,则由线面垂直的性质得n⊥m,故C正确;
在D中,若直线n∥m,则由线面垂直的判定定理得n⊥α,故D正确.
故选:A.
14.【解答】解:根据双曲线的图象关于x轴,y轴和原点对称可知,与直线2x﹣y+2=0关于原点对称的直线2x﹣y﹣2=0被双曲线C所截得的弦长等于3;
与直线2x﹣y+2=0关于y轴对称的直线2x+y﹣2=0被双曲线C所截得的弦长等于3;
与直线2x﹣y+2=0关于x轴对称的直线2x+y+2=0被双曲线C所截得的弦长等于3;
故选:A.
15.【解答】解:过A作AD垂直于桌面,垂足为D,连CD,BD,
∵AC⊥BC,根据三垂线定理得CD⊥BC,
∴∠ACD=60°,
设BC=x,则AC=x,AB=2x,
∴AD=AC=×x=x,
所以AB边所在直线与桌面所成角为∠ABD,
∵sin∠ABD===,
所以∠ABD=racsin.
故选:D.
16.【解答】解:平面α的法向量为=(1,2,﹣2),
联立方程组,令x=1,得y=﹣2,z=2,
令x=3,得y=1,z=8,
故点P(1,﹣2,2)和点Q(3,1,8)为直线l的两个点,
∴=(2,3,6)为直线l的方向向量,
∵cos<,>===﹣,
∴直线l与平面α所成角的正弦值为,
故选:B.
三、解答题(本大题共4题,共52分,解答时写出必要的步骤)
17.【解答】解:(1)依题意设抛物线C的方程为y2=2px,将A(4,4)代入得p=2,所以抛物线C的方程为y2=4x.
(2)F(1,0),直线l:y=x﹣1,
联立得x2﹣6x+1=0,
设A(x1,y1),B(x2,y2),
则x1+x2=6,
根据抛物线的定义可得|MN|=x1+x2+p=6+2=8.
18.【解答】解:(1)过点O作AB的平行线CO,且使CO=AB,连结BO,DO,
则∠DCO是异面直线AB和CD所成角,
∵CO=AB=2,CD=4,∴∠DCO=60°,
∴异面直线AB和CD所成的角的大小为60°.
证明:(2)设BC∩α=P,连结MN、MP、PN,
∵AB是异面直线a、b的公垂线,AB⊥平面α,
∴AC⊥AB,MP⊥AB,
∵MP?平面ABC,AB?平面ABC,AC?平面ABC,
∴MP∥AC,
∵MP?α,AC?α,∴直线a∥α.
∵a∥α,∴b∥α,∴PN∥BD,
∵MP∥AC,M是AB中点,∴P是BC中点,∴N是CD中点,
∴CN=DN.
19.【解答】解:(1)F(2,0)
当直线AB垂直于x轴时,直线AB的方程为:x=2,可得A(2,)或A(2,﹣),
∴直线AD的方程为2﹣y﹣3=0或2x+y﹣3=0
(2)设直线AB的方程为x=ty+2代入x2﹣y2=2得(t2﹣1)y2+4ty+2=0,
设A(x1,y1),B(x2,y2),
则y1+y2=﹣,y1y2=,
直线AD的方程为:=,令x=1得y=y1+y1×=y1(1+)
∴y=y1(1+)=(1+)
=y2,
∴FD∥BE.
20.【解答】解:(1)假设在AB上存在点E,使得AB⊥平面ECD,
∵在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,
AB⊥CD,AB=10,CD=6.
作CE⊥AB,交AB于E,连结DE,
又CE∩CD=C,
∴AB⊥平面ECD.
(2)由(1)知AB⊥平面CDE,故AB⊥DE,AB⊥CE,
∴CED为二面角C﹣AB﹣D的平面角,
∵AB=10,CD=6,S△ABC=S△ABD=30,
∴,
解得DE=CE=6,又CD=6,
∴△CDE是等边三角形,
∴∠CED=60°,
即二面角C﹣AB﹣D的大小为60°.
(3)由(1)知AB⊥平面CDE,故VA﹣BCD=S△CDE?AB=S△CDE,
∵△ABD和△ABC都是以AB为斜边的直角三角形,且由(1)知AB⊥平面CDE,
∴CE=DE,
设CE=DE=m,则E到CD的距离d=,
∴S△CDE==3,
∵△ABD是直角三角形,∴D在以AB为直径的圆上,故DE的最大值为AB=5,
即0<m≤5,
∴S△CDE的最大值为3=12,
∴三棱锥A﹣BCD体积的最大值为=40.
21.【解答】解:(1)∵k+b=﹣,∴b=﹣k﹣,∴y=kx﹣k﹣=k(x﹣1)﹣,
所以动直线l过定点(1,﹣).
(2)联立消去y得(1+2k2)x2+4kbx+2b2﹣2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=﹣,x1x2=,
∵∠ADB=,又D(0,1),
∴(x1,y1﹣1)?(x2,y2﹣1)=x1x2+(y1﹣1)(y2﹣1)=x1x2+(kx1+b﹣1)(kx2+b﹣1)
=x1x2+k2x1x2+(b﹣1)2+k(b﹣1)(x1+x2)
=(1+k2)x1x2+k(b﹣1)(x1+x2)+(b﹣1)2
=(1+k2)×+k(b﹣1)×+(b﹣1)2
=(b﹣1),
∴(b﹣1)=0,又b≠1(否则直线l过D),
∴b=﹣,所以动直线l过定点(0,﹣)
(3)b=﹣,直线l为:y=kx﹣,
由(2)知x1+x2=,x1x2=,
经过A(x1,y1),B′(﹣x2,y2)的直线方程为:=,
∴=,
令x=0得y﹣(kx1﹣)=k(x2﹣x1)?,
∴y=kx1﹣+k?=﹣=﹣﹣=﹣2
所以直线AB′是过定点(0,﹣2).
一、填空题(本大题共12题,每题3分,共36分)
1.(3分)过点(1,0)且与直线x﹣y=0平行的直线方程是 .
2.(3分)将边长分别为1cm和2cm的矩形,绕边长为2cm的一边所在的直线旋转一周得到一圆柱,则该圆柱的侧面积为 cm2.
3.(3分)以A(1,1),B(3,﹣1)为直径的端点的圆的方程是 .
4.(3分)正方体的外接球体积为V1,其内切球体积为V2,则的值为 .
5.(3分)椭圆的长轴长是短轴长的2倍,它的一个焦点为(,0),则椭圆的标准方程是 .
6.(3分)已知正四棱锥的底面边长是2,侧棱长是,则该正四棱锥的全面积为 .
7.(3分)双曲线﹣=1(a>0)的一条渐近线方程为y=2x,则a的值为 .
8.(3分)点P是棱长为a的正方体ABCD﹣A1B1C1D1棱A1B1上的动点,则四棱锥P﹣ABC1D1的体积为 .
9.(3分)已知椭圆+=1(m>0)和曲线﹣=1(n>0)有相同的焦点F1、F2,点P为椭圆和双曲线的一个交点,则|PF1|?|PF2|的值是 .
10.(3分)正方形铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径圆弧,剪下一个顶角为的扇形,用这块扇形铁片围成一个圆锥形容器,则这个圆锥形容器的容积等于 cm3.
11.(3分)在棱长为a的正方体ABCD﹣A1B1C1D1中,M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心,则过点M、N、P的平面截正方体的截面面积为 .
12.(3分)在平面直角坐标系xOy中,C为直线y=5上的动点,以C为圆心的圆C截y轴所得的弦长恒为6,过原点O作圆C的一条切线,切点为P,则点P到直线3x+4y﹣25=0的距离的最小值为 .
二、选择题(本大题共4题,每题3分,共12分)
13.(3分)直线m⊥平面α,下面判断错误的是( )
A.若直线n⊥m,则n∥α B.若直线n⊥α,则n∥m
C.若直线n∥α,则n⊥m D.若直线n∥m,则n⊥α
14.(3分)已知直线1:2x﹣y+2=0被双曲线C:x2﹣=1截得的线段长等于3,下面哪一条直线被双曲线C所截得的弦长不等于3( )
A.l:2y﹣x+2=0 B.l:﹣2x﹣y+2=0
C.l:2x+y+2=0 D.l:2x﹣y﹣2=0
15.(3分)有一把三角尺ABC,∠A=30°,∠C=90°,把边BC放置在桌面上,当三角尺与桌面所在的平面成60°的时候,AB边所在的直线与桌面所成的角等于( )
A.arcsin B. C. D.arcsin
16.(3分)阅读材料:空间直角坐标系O﹣xyz中,过点P(x0,y0,z0)且一个法向量为=(a,b,c)的平面α的方程为a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;过点P(x0,y0,z0)且个方向向量为=(u,v,w)(uvw≠0)的直线l的方程为==,阅读上面材料,并解决下面问题:已知平面α的方程为x+2y﹣2z﹣4=0,直线l是两平面3x﹣2y﹣7=0与2y﹣z+6=0的交线,则直线l与平面α所成角的大小为( )
A.arcsin B.arcsin
C.arcsin D.arcsin
三、解答题(本大题共4题,共52分,解答时写出必要的步骤)
17.(8分)抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
18.(8分)如图,AB是异面直线a、b的公垂线,长度为2,点C、D分别在直线a和b上,且CD长为4,过线段AB的中点M作平面α,使得AB⊥平面α,线段CD与平面α交点为N.
(1)求异面直线AB和CD所成的角的大小;
(2)求证:直线a∥α且CN=DN.
19.(10分)过双曲线C:﹣=1的右焦点F且与x轴不重合的直线交双曲线C于A、B两个点,定点D(,0).
(1)当直线AB垂直于x轴时,求直线AD的方程.
(2)设直线AD与直线x=1相交于点E,求证:FD∥BE.
20.(12分)在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,AB⊥CD,AB=10,CD=6.
(1)问在AB上是否存在点E,使得AB⊥平面ECD?
(2)如果S△ABC=S△ABD=30,求二面角C﹣AB﹣D的大小.
(3)求三棱锥A﹣BCD体积的最大值.
21.(14分)已知椭圆C:+y2=1,直线l:y=kx+b与椭圆C相交于A、B两点.
(1)如果k+b=﹣,求动直线l所过的定点;
(2)记椭圆C的上顶点为D,如果∠ADB=,证明动直线l过定点P(0,﹣);
(3)如果b=﹣,点B关于y轴的对称点为B',向直线AB'是过定点?如果是,求出定点的坐标;如果不是,请说明理由.
2018-2019学年上海市虹口区高二(下)期中数学试卷
参考答案与试题解析
一、填空题(本大题共12题,每题3分,共36分)
1.【解答】解:设与直线x﹣y=0平行的直线方程是x﹣y+m=0,
且直线过点(1,0),则1﹣0+m=0,解得m=﹣1,
所以所求直线方程是x﹣y﹣1=0.
故答案为:x﹣y﹣1=0.
2.【解答】
解:依题意,将该圆柱的侧面展开,则展开图是以2π为长,以2为宽的矩形,
所以该圆柱的侧面积为S=2π×2=4π.
故填:4π.
3.【解答】解:点A(1,1),B(3,﹣1),则AB的中点为M(2,0),
AB的长为|AB|==2,
所以以AB为直径的端点的圆的圆心为M,半径为,
所求圆的方程是(x﹣2)2+y2=2.
故答案为:(x﹣2)2+y2=2.
4.【解答】解:设正方体的棱长为2a,
则其外接球的半径为,
内切球的半径为a,
则,.
∴.
故答案为:.
5.【解答】解:依题意得2a=4b,c=,又a2=b2+c2,
∴a=1,b=1,
故答案为:+y2=1.
6.【解答】解:如图在正四棱锥S﹣ABCD中,O为底面正方形的中心,E为BC的中点,连接OE,SO,SE,
则SO⊥平面ABCD,又BC?平面ABCD,所以BC⊥SO,
在三角形ABC中,O,E分别为AC,BC的中点,所以OE∥AB,又因为AB⊥BC,所以BC⊥OE.
又OE∩SO=0,所以BC⊥平面SOE,因为SE?平面SOE,
所以SE⊥BC,即SE为侧面SBC的斜高,
三角形SBE为直角三角形,所以SE===2.
所以该正四棱锥的全面积S全=SABCD+4×SSBC=2×2+4×=4+8=12.
故填:12.
7.【解答】解:双曲线=1(a>0)的一条渐近线方程为y=2x,
可得:,解得a=1.
故答案为:1.
8.【解答】解:连接B1C交BC1于点O,显然OB1=B1C=BC1=a,
∵四边形BCC1B1是正方形,∴BC1⊥B1C,
∵AB⊥平面BCC1B1,∴AB⊥B1O,
又AB∩BC1=B,
∴OB1⊥平面ABC1D1,
∵A1B1∥AB,∴A1B1∥平面ABC1D1,
∴P到平面ABC1D1的距离等于B1O,
∴V===.
故答案为:.
9.【解答】解:∵已知椭圆+=1(m>0)和曲线﹣=1(n>0)有相同的焦点F1、F2,
∴m2﹣9=n2+4,即m2﹣n2=13,
假设P在第一象限,根据椭圆和双曲线的定义可得:|PF1|+|PF2|=2m,|PF1|﹣|PF2|=2n,
两式平方差得4|PF1|?|PF2|=4m2﹣4n2=4×13,∴|PF1|?|PF2|=13.
故答案为13.
10.【解答】
解:依题意,设该圆锥的母线长为l,则l=4,
设底面圆的半径为r,则2πr==2π,解得r=1,
所以圆锥的高h==,
所以这个圆锥形容器的容积V=×πr2×h==π.
故填:.
11.【解答】解:依题意,M、N、P分别是正方形ABCD、正方形BB1C1C和正方形ABB1A1的中心,即M,N,P分别为AB1、B1C、AC的中点,
所以过点M、N、P的平面截正方体的截面为三角形AB1C,如图.
因为正方体的棱长为a,所以三角形AB1C,的边长为a,所以三角形AB1C,的面积为:S==.
故填:.
12.【解答】解:根据题意,设C的坐标为(m,5),圆C的半径为r,
又由圆C截y轴所得的弦长恒为6,则点(0,2)在圆C上,则r2=m2+9,
又由过原点O作圆C的一条切线,切点为P,则|CP|2=r2=m2+9,
|OC|2=m2+25,
则|OP|2=|OC|2﹣|CP|2=(m2+25)﹣(m2+9)=16,
则P在以O为圆心,半径为4的圆上,
其圆心O到直线3x+4y﹣25=0的距离d==5,
则P到直线3x+4y﹣25=0的距离的最小值为d﹣r=5﹣4=1,
故答案为:1
二、选择题(本大题共4题,每题3分,共12分)
13.【解答】解:由直线m⊥平面α,得:
在A中,若直线n⊥m,则由线面平行性质得n与α相交、平行或n?α,故A错误;
在B中,若直线n⊥α,则由线面垂直的性质得n∥m,故B正确;
在C中,若直线n∥α,则由线面垂直的性质得n⊥m,故C正确;
在D中,若直线n∥m,则由线面垂直的判定定理得n⊥α,故D正确.
故选:A.
14.【解答】解:根据双曲线的图象关于x轴,y轴和原点对称可知,与直线2x﹣y+2=0关于原点对称的直线2x﹣y﹣2=0被双曲线C所截得的弦长等于3;
与直线2x﹣y+2=0关于y轴对称的直线2x+y﹣2=0被双曲线C所截得的弦长等于3;
与直线2x﹣y+2=0关于x轴对称的直线2x+y+2=0被双曲线C所截得的弦长等于3;
故选:A.
15.【解答】解:过A作AD垂直于桌面,垂足为D,连CD,BD,
∵AC⊥BC,根据三垂线定理得CD⊥BC,
∴∠ACD=60°,
设BC=x,则AC=x,AB=2x,
∴AD=AC=×x=x,
所以AB边所在直线与桌面所成角为∠ABD,
∵sin∠ABD===,
所以∠ABD=racsin.
故选:D.
16.【解答】解:平面α的法向量为=(1,2,﹣2),
联立方程组,令x=1,得y=﹣2,z=2,
令x=3,得y=1,z=8,
故点P(1,﹣2,2)和点Q(3,1,8)为直线l的两个点,
∴=(2,3,6)为直线l的方向向量,
∵cos<,>===﹣,
∴直线l与平面α所成角的正弦值为,
故选:B.
三、解答题(本大题共4题,共52分,解答时写出必要的步骤)
17.【解答】解:(1)依题意设抛物线C的方程为y2=2px,将A(4,4)代入得p=2,所以抛物线C的方程为y2=4x.
(2)F(1,0),直线l:y=x﹣1,
联立得x2﹣6x+1=0,
设A(x1,y1),B(x2,y2),
则x1+x2=6,
根据抛物线的定义可得|MN|=x1+x2+p=6+2=8.
18.【解答】解:(1)过点O作AB的平行线CO,且使CO=AB,连结BO,DO,
则∠DCO是异面直线AB和CD所成角,
∵CO=AB=2,CD=4,∴∠DCO=60°,
∴异面直线AB和CD所成的角的大小为60°.
证明:(2)设BC∩α=P,连结MN、MP、PN,
∵AB是异面直线a、b的公垂线,AB⊥平面α,
∴AC⊥AB,MP⊥AB,
∵MP?平面ABC,AB?平面ABC,AC?平面ABC,
∴MP∥AC,
∵MP?α,AC?α,∴直线a∥α.
∵a∥α,∴b∥α,∴PN∥BD,
∵MP∥AC,M是AB中点,∴P是BC中点,∴N是CD中点,
∴CN=DN.
19.【解答】解:(1)F(2,0)
当直线AB垂直于x轴时,直线AB的方程为:x=2,可得A(2,)或A(2,﹣),
∴直线AD的方程为2﹣y﹣3=0或2x+y﹣3=0
(2)设直线AB的方程为x=ty+2代入x2﹣y2=2得(t2﹣1)y2+4ty+2=0,
设A(x1,y1),B(x2,y2),
则y1+y2=﹣,y1y2=,
直线AD的方程为:=,令x=1得y=y1+y1×=y1(1+)
∴y=y1(1+)=(1+)
=y2,
∴FD∥BE.
20.【解答】解:(1)假设在AB上存在点E,使得AB⊥平面ECD,
∵在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,
AB⊥CD,AB=10,CD=6.
作CE⊥AB,交AB于E,连结DE,
又CE∩CD=C,
∴AB⊥平面ECD.
(2)由(1)知AB⊥平面CDE,故AB⊥DE,AB⊥CE,
∴CED为二面角C﹣AB﹣D的平面角,
∵AB=10,CD=6,S△ABC=S△ABD=30,
∴,
解得DE=CE=6,又CD=6,
∴△CDE是等边三角形,
∴∠CED=60°,
即二面角C﹣AB﹣D的大小为60°.
(3)由(1)知AB⊥平面CDE,故VA﹣BCD=S△CDE?AB=S△CDE,
∵△ABD和△ABC都是以AB为斜边的直角三角形,且由(1)知AB⊥平面CDE,
∴CE=DE,
设CE=DE=m,则E到CD的距离d=,
∴S△CDE==3,
∵△ABD是直角三角形,∴D在以AB为直径的圆上,故DE的最大值为AB=5,
即0<m≤5,
∴S△CDE的最大值为3=12,
∴三棱锥A﹣BCD体积的最大值为=40.
21.【解答】解:(1)∵k+b=﹣,∴b=﹣k﹣,∴y=kx﹣k﹣=k(x﹣1)﹣,
所以动直线l过定点(1,﹣).
(2)联立消去y得(1+2k2)x2+4kbx+2b2﹣2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=﹣,x1x2=,
∵∠ADB=,又D(0,1),
∴(x1,y1﹣1)?(x2,y2﹣1)=x1x2+(y1﹣1)(y2﹣1)=x1x2+(kx1+b﹣1)(kx2+b﹣1)
=x1x2+k2x1x2+(b﹣1)2+k(b﹣1)(x1+x2)
=(1+k2)x1x2+k(b﹣1)(x1+x2)+(b﹣1)2
=(1+k2)×+k(b﹣1)×+(b﹣1)2
=(b﹣1),
∴(b﹣1)=0,又b≠1(否则直线l过D),
∴b=﹣,所以动直线l过定点(0,﹣)
(3)b=﹣,直线l为:y=kx﹣,
由(2)知x1+x2=,x1x2=,
经过A(x1,y1),B′(﹣x2,y2)的直线方程为:=,
∴=,
令x=0得y﹣(kx1﹣)=k(x2﹣x1)?,
∴y=kx1﹣+k?=﹣=﹣﹣=﹣2
所以直线AB′是过定点(0,﹣2).
同课章节目录
