21.3 实际问题与一元二次方程课件(73张PPT)
文档属性
| 名称 | 21.3 实际问题与一元二次方程课件(73张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 23:31:01 | ||
图片预览









文档简介
九年级数学上册
21.3 实际问题与一元二次方程
第一课时
第二课时
第三课时
第一课时
实际问题与一元二次方程
(1)
返回
传染病,一传十,
十传百… …
【想一想】有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
导入新知
素养目标
1.能根据实际问题中的数量关系,正确列出一元二次方程.
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
列一元二次方程解决实际问题
有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
你能解决这个问题吗?
探究新知
知识点 1
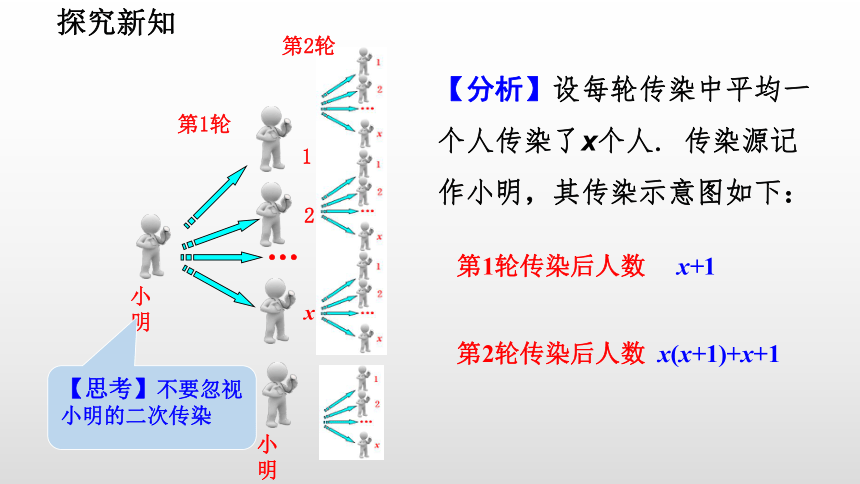
问题1
第2轮
???
小明
1
2
x
第1轮
第1轮传染后人数 x+1
小明
第2轮传染后人数 x(x+1)+x+1
【思考】不要忽视小明的二次传染
探究新知
【分析】设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
根据示意图,列表如下:
解:设每轮传染中平均一个人传染了x个人.
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
列方程 x+1+x(x+1)=121
化简得 x2+2x-120=0
(x-10)(x+12)=0
x1=10, x2=-12(舍)
列方程 x+1+x(x+1)=121
提取公因式 (x+1)(x+1)=121
(x+1)2=121
x+1=±11一定要进行检验
x1=10, x2=-12(舍)
有更简单的方法解这个方程吗?
答:平均一个人传染了________个人.
10
注意:一元二次方程的解有可能不符合题意,所以舍去.
探究新知
【想一想】如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法 以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331人.
第一轮传染后的人数 第二轮传染后的
人数 第三轮传染后的
人数
(1+x)1 (1+x)2
【分析】
第1种做法 以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331人.
(1+x)3
探究新知
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1?x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第n轮
【思考】如果按这样的传染速度,n轮后传染后有多少人患了流感?
(1+x)2
(1+x)n
(1+x)3
经过n轮传染后共有 (1+x)n 人患流感.
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x=
探究新知
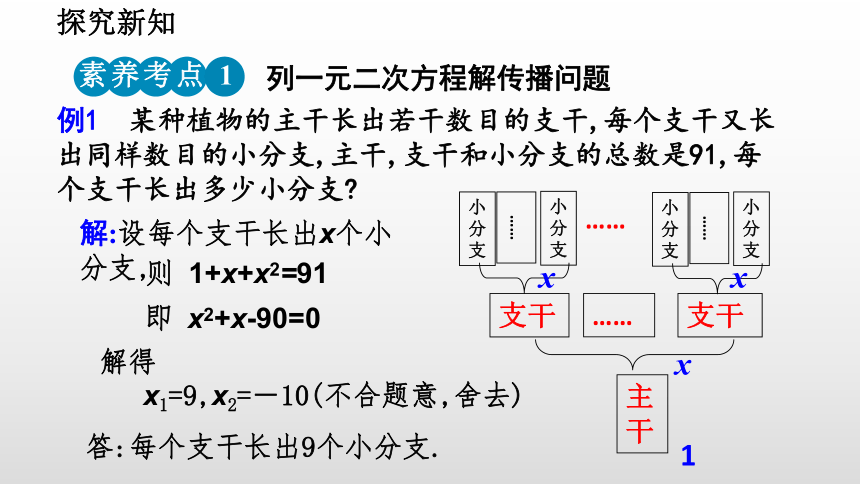
例1 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即 x2+x-90=0
解得
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
列一元二次方程解传播问题
素养考点 1
探究新知
1.在分析引例和例1中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
【思考】
探究新知
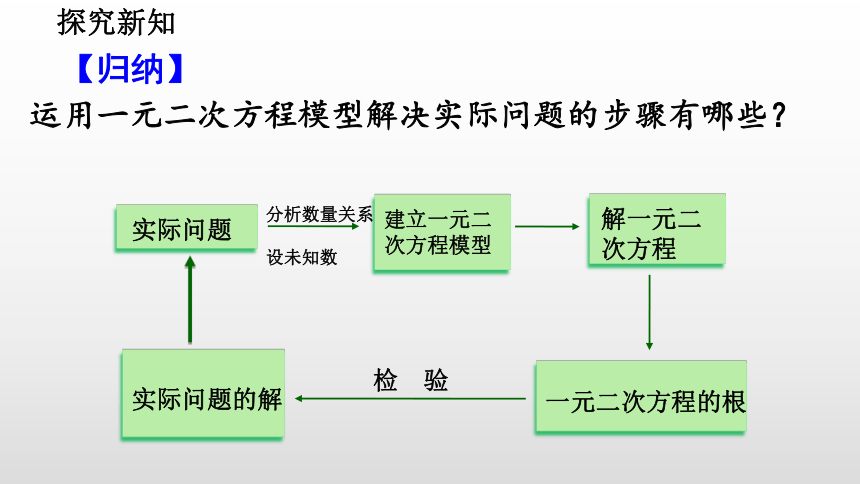
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
【归纳】
探究新知
电脑勒索病毒的传播非常快,如果开始有6台电脑被感染,经过两轮感染后共有2400台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染x台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得=19 或 =-21 (舍去)
依题意 6+6x+6x (1+x) =2400
6 (1+x)? =2400
巩固练习
变式题1
例2 一个小组若干人,新年互送贺卡,若全组共送贺卡72张,则这个小组共多少人?
解:
设这个小组共x人,
根据题意列方程,得
x(x-1)=72
化简,得 x2-x-72=0
解方程,得 x1=9, x2=-8(舍去)
答:这个小组共9人.
列一元二次方程解相互类问题
素养考点 2
探究新知
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,求全组有多少名同学?
解:全组有x名同学,根据题意,得
x(x-1)=182
解得 x1=14,x2=-13(不合题意,舍去)
答:全组有14名同学.
巩固练习
变式题2
1.(2018?绵阳中考在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )
A.9人 B.10人 C.11人 D.12人
解析 设参加酒会的人数为x人,甲跟乙碰杯与乙跟甲碰杯算一次,根据题意得:
x(x﹣1)=55,整理,得:x2﹣x﹣110=0,
解得:x1=11,x2=﹣10(不合题意,舍去).
连接中考
巩固练习
连接中考
C
解析 设共有x个班级参赛,甲班跟乙班比赛与乙班跟甲班比赛算一次,根据题意得: =15,解得:x1=6,x2=﹣5(不合题意,舍去),则共有6个班级参赛.
连接中考
2.(2018?中考)某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?( )
A.4 B.5 C.6 D.7
巩固练习
C
1.元旦将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A.x2=1980 B. x(x+1)=1980
C. x(x-1)=1980 D.x(x-1)=1980
D
课堂检测
基础巩固题
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)?=73
B
课堂检测
基础巩固题
3.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在一天内,一人平均能传染x人,经过两天传染后128人患上甲肝,则x的值为( )?
A.10 B.9 C.8 D.7
D
课堂检测
基础巩固题
1. 为了宣传环保,小明写了一篇倡议书,决定用微博转发的方式传播,他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发倡议书,每个好友转发倡议书之后,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有111个人参与了传播活动,则n=______.
10
课堂检测
能力提升题
2. 某校初三各班进行篮球比赛(单循环制),每两班之间共比赛了6场,求初三有几个班?
解:初三有x个班,根据题意列方程,得
化简,得 x2-x-12=0
解方程,得 x1=4, x2=-3(舍去)
答:初三有4个班.
课堂检测
分析:设每轮分裂中平均每个有益菌可分裂出x个有益菌
60
60x
60(1+x)
60(1+x)
60(1+x)x
3. 某生物实验室需培育一群有益菌,现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
(1)每轮分裂中平均每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
课堂检测
传染源 本轮分裂成有益菌数目 本轮结束有益菌总数
第一轮
第二轮
第三轮
解:设每个有益菌一次分裂出x个有益菌
60+60x+60(1+x)x=24000
x1=19,x2=-21(舍去)
因此每个有益菌一次分裂出19个有益菌.
三轮后有益菌总数为 24000×(1+19)=480000.
课堂检测
解:设每天平均一个人传染了x人,
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2187,
(1+x)7= (1+2)7=2187.
课堂检测
4. 甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同:审题、设元、列方程、解方程、检验、作答.不同的地方是要检验根的合理性.
传播问题
数量关系:
第一轮传播后的量=传播前的量×(1+传播速度)
第二轮传播后的量=第一轮传播后的量×(1+传播速度)=传播前的量×(1+传播速度)2
数字问题
相互问题1
相互问题2
关键要设数位上的数字,要准确地表示出原数.
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2.
甲送乙照片与乙送甲照片是要两张照片,故总数不要除以2.
步骤
类型
课堂小结
第二课时
实际问题与一元二次方程
(2)
返回
【想一想】两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【思考】有关增长/下降率问题,应该如何解答呢?
导入新知
素养目标
1. 能正确列出关于增长率问题的一元二次方程.
2. 通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
有关增长/下降率的问题
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【思考】下降率是什么意思?它与原成本、终成本之间有何数量关系?
探究新知
知识点 1
问题1
【分析】甲种药品成本的年平均下降额为
乙种药品成本的年平均下降额为
乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率.
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为 元,两年后甲种药品成本为 元,
5000(1-x)
5000(1-x)2
依题意得 :5000(1-x)? =3000
解方程,得:
答:甲种药品成本的年平均下降率约22.5%.
探究新知
设乙种药品成本的年平均下降率为y,
一年后乙种药品成本为 元,
两年后乙种药品成本为 元
依题意得, ,
解方程得 ,
6000(1-y)
6000(1-y)2
6000(1-y)2=3600
答:乙种药品成本的年平均下降率约为 .
y1≈0.225,y1≈-1.775
22.5%
探究新知
【思考】为什么选择22.5%作为答案?比较两种药品成本的年平均下降率.经过计算,你能得出什么结论?成本下降额较大的药品,它的成本下降率一定也较大吗?应怎样全面地比较对象的变化状况?
答:经过计算,甲乙两种药品的平均下降率相同 .成本下降额较大的药品,它的成本下降率不一定较大,应比较降前及降后的价格.
探究新知
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的量是a,增长(或降低)n次后的量是A,则它们的数量关系可表示为
其中增长取“+”,降低取“-”
探究新知
【归纳】
=A
例4 某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
列一元二次方程解答增长率问题
素养考点 1
探究新知
某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.求平均每次降价的百分率?
解:设平均每次降价的百分率为x,根据题意得:
36(1- x )2=25
解得
答:平均每次约降价16.7%.
巩固练习
变式题1
1.(2018?中考)某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )
A.80(1+x)2=100 B.100(1﹣x)2=80
C.80(1+2x)=100 D.80(1+x2)=100
解析 由题意知,蔬菜产量的年平均增长率为x,根据2016年蔬菜产量为80吨,则2017年蔬菜产量为80(1+x)吨,2018年蔬菜产量为80(1+x)(1+x)吨,预计2018年蔬菜产量达到100吨,即:80(1+x)(1+x)=100或80(1+x)2=100.
A
巩固练习
连接中考
2.(2018?中考)某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
A.2% B.4.4% C.20% D.44%
解析 设该市2018年、2019年“竹文化”旅游收入的年平均增长率为x,根据题意得:2(1+x)2=2.88,解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
C
巩固练习
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720
C.500(1+x2)=720 D.720(1+x)2=500
B
课堂检测
基础巩固题
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为
课堂检测
2(1+x)+2(1+x)2=8
基础巩固题
受益于国家支持新能源汽车发展和“一带一路”倡议等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计:2014年利润为2亿元,2016年利润为2.88亿元.
(1)求该企业从2014年到2016年的平均增长率.
(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?
解:(1)设年平均增长率为x,依题意得:(2+x)2=2.88.
(2)该企业2017年的利润为2.88×(1+20%)=3.456(亿元).
因为3.456>3.4.
所以该企业2017年的利润能否超过3.4亿元.
课堂检测
能力提升题
某电脑公司2001年的各项经营,一月份的营业额为200万元,一、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率。
分析:设这个增长率为x,一月份的营业额200万元,二月份的营业额是 万元、三月份的营业额 万元,由三月份的总营业额列出等量关系.
200(1+x)
200(1+x)2
解:设平均增长率为x,得
200 + 200(1+x) + 200(1+x)2 = 950
整理,得
200x2 + 600x = 350
解得 x1≈0.5,x2≈-3.5(舍去)
答:这个增长率是50%。
拓广探索题
课堂检测
增长(下降)率问题
增长率问题
下降率问题
基数为a,平均增长/下降率为x
第一次增长
第二次增长
第n次增长
第一次下降
第二次下降
第n次下降
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
a(1±x)n
课堂小结
第三课时
实际问题与一元二次方程
(3)
返回
【思考】通过上节课的学习,请谈谈列方程解应用题的一般步骤是怎样的?关键是什么?
步骤:①审题;②设元;③列式;④解答;⑤验根;⑥答案.
导入新知
【思考】现有长19cm,宽为15cm长方形硬纸片,将它的四角各剪去一个同样大小的正方形后,再折成一个无盖的长方形纸盒,要使纸盒的底面积为77cm?,问剪去的小正方形的边长应是多少?
解:设剪去的小正方形的边长为xcm,则纸盒的长为(19-2x),宽为(15-2x)cm,依题意得(19-2x)(15-2x)=77 ;
整理得:x?-17x+52=0;
解方程,得:(x-13)(x-4)=0;
解得:x1=4,x2=13(舍去);
因此剪去的小正方形的边长应为3cm.
导入新知
素养目标
1.能正确利用面积关系列出关于几何图形的一元二次方程.
2.进一步深入体会一元二次方程在实际生活中的应 用,经历将实际问题转化为数学问题的过程,提 高数学应用意识.
几何图形的面积问题
广东省怀集县马宁镇初级中学 徐志才
如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?
27cm
21cm
探究新知
知识点 1
问题1
广东省怀集县马宁镇初级中学 徐志才
解法一:依据题意知,中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意得:中央矩形的长为 cm,宽为 cm.
因为四周的彩色边衬所点面积是封面面积的______,则中央矩形的面积是封面面积的____.
(27-18x)
(21-14x)
所以可列方程得: (27-18x)(21-14x) = ×27×21
整理,得 16x2-48x+9=0
解方程,得 x= ,x1≈2.8cm,x2≈0.2
所以,9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm
因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.
探究新知
解法二:设正中央的矩形两边分别为9xcm,7xcm,
列方程得:
解得 x 2.6
上、下的边衬的宽为(27-9 2.6) 0.5=1.8cm
左、右的边衬的宽为(21-7 2.6) 0.5=1.4cm
探究新知
例1 有一张长6尺,宽3尺的长方形桌子,现用一块长方形台布铺在桌面上,如果台布的面积是桌面面积的2倍,且四周垂下的长度相同,试求这块台布的长和宽各是多少?(精确到0.1尺)
解:设四周垂下的宽度为x尺时,则台布的长为(2x+6)尺,宽为(2x+3)尺,依题意得:(6+2x)(3+2x)=2×6×3
整理方程得:2x?+9x-9=0
解得:x1≈0.84,x2≈-5.3(不合题意,舍去)
因此:台布的长为:2×0.84+6≈7.7(尺)
台布的宽为:2×0.84+3≈4.7(尺)
即这块台布的长约为7.7尺,宽约为4.7尺.
利用一元二次方程解答一般面积问题
素养考点 1
探究新知
变式题1
要为一幅长29cm,宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框的宽度应是多少厘米(结果保留小数点后一位)?
解:设镜框的宽为xcm,根据题意,得
整理得8x2+204x-319=0,解得 .
∴x1= ,x2= (不合题意,舍去). ∴x= ≈1.5.
答:镜框的宽度约为1.5cm.
巩固练习
例2 如右图是长方形鸡场的平面示意图。一边靠墙,另三边用竹篱笆围成,且竹篱笆总长为35m。
(1)若所围的面积为150m?,试求此长方形鸡场的长和宽;
A
B
C
D
解:设BC=xcm,则AB=CD= (35-x),依题意可列方程:
(35-x)x=150.整理得:x2-35x+300=0,
解方程,得(x-20)(x-15)=0
即:x1=20,x2=15. 当BC=x=20m时,AB=CD=7.5m,
当BC=15m时,AB=CD=10m,即这个长方形鸡场的长与
宽分别为20m和7.5m或15m和10m。
靠墙问题的解答
素养考点 2
探究新知
(2)如果墙长为18m,则(1)中长方形鸡场的长和宽分别是多少?
解:当墙长为18m时,显然BC=20m时,所围成的鸡场会在靠墙处留下一个缺口,不合题意,应舍去,此时所围成的长方形鸡场的长与宽值能是15m和10m.
点拨:在寻找关系式时,切记三边之和等于总长,而不是四边之和等于总长.
探究新知
(3)能围成面积为160m?的长方形鸡场吗?说说你的理由。
解:不能围成面积为160m?的长方形鸡场,理由如下:
设BC=xm,由(1)知AB=(35-x),从而有(35-x)x=160,方程整理为x?-35x+320=0.此时Δ=35?-4×1×320=-55<0,原方程没有实数根,从而知用35m的篱笆按图示方式不能围成面积为160m?的鸡场。
探究新知
变式题2 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80平方米?
住房墙
1m
解:设矩形猪舍垂直于住房墙的一边长为x m,
由题意得 x(25-2x+1)=80
整理,得 x2-13x+40=0
解方程,得 (x-5)(x-8)=0
即: x1=5 , x2=8
当x=5时,26-2x=16>12 (舍去);当x=8时,26-2x=10<12
故所围矩形猪舍的长为10m,宽为8m.
则平行于住房墙的一边长(25-2x+1)m.
巩固练习
20
32
x
x
解:设道路的宽为x米,依题意得
例3 如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
还有其他方法吗?
修路问题的图形面积
20×32-32x-20x+x2=540
素养考点 3
探究新知
解:设道路的宽为 x 米
20
32
x
x
20-x
32-x
(32-x)(20-x)=540
整理,得x2-52x+100=0
解方程,得(x-50)(x-2)=0
即 x1=2,x2=50
当x=50时,32-x=-18,不合题意,舍去.
∴取x=2
答:道路的宽为2米.
方法二
探究新知
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540㎡,求这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-x)(20-x)=540
可列方程为
变式一
探究新知
20
32
x
x
x
20-x
如图,在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-x)=540
可列方程为
变式二
32-2x
探究新知
20
32
x
x
x
x
20
32
2x
2x
32-2x
20-2x
如图,在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-2x)=540
可列方程为
变式三
探究新知
在宽为20m, 长为32m的矩形地面上修筑四条道路,余下的部分种上草坪,如果横、纵小路的宽度比为3:2,且使小路所占面积是矩形面积的四分之一,求道路的宽为多少?
变式四
探究新知
小路所占面积是矩形面积的四分之一
剩余面积是矩形面积的四分之三
解:设横、竖小路的宽度分别为3x、 2x,
于是可列方程
(30-4x)(20-6x)= —×20×30
20㎝
30㎝
3x
2x
30-4x
20-6x
4
3
3x
2x
6x
4x
30-4x
20-6x
探究新知
我们利用“图形经过移动,它的面积大小不会改变”的性质,把纵、横两条路移动一下,使列方程容易些(目的是求出结果,至于实际施工,仍可按原图的位置进行).
方法点拨
探究新知
如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
巩固练习
变式题3
解:设道路宽为x米,
依题意得
整理得,x2-36x+35=0
其中的 x=35超出了原矩形的宽,应舍去.
答:道路的宽为1米.
(32-2x)(20-x)=570
解方程,得(x-35)(x-1)=0
即:x1=35,x2=1
巩固练习
(2018?中考)公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
A.(x+1)(x+2)=18 B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18 D.x2+3x+16=0
解析 设原正方形的边长为xm,依题意有
(x﹣1)(x﹣2)=18,故选C.
巩固练习
连接中考
C
1. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
80cm
x
x
x
x
50cm
B
课堂检测
基础巩固题
2.一块长方形铁板,长是宽的2倍,如果在4个角上截去边长为5cm的小正方形,然后把四边折起来,做成一个没有盖的盒子,盒子的容积是3000 cm3,求铁板的长和宽.
解:设铁板的宽为x cm,则有长为2x cm,依题意得:
5(2x-10)(x-10)=3000; 整理得:x2-15x-250=0;
解方程,得:(x-25)(x+10)=0;
即: x1=25 x2=-10(舍去);所以 2x=50
答:铁板的长50cm,宽为25cm.
课堂检测
解:设AB长是x m,依题意得: (100-4x)x=400
整理得:x2-25x+100=0
解方程得:(x-20)(x-5)=0
即 x1=5,x2=20
x=20,100-4x=20<25 ; x=5,100-4x=80>25 x=5(舍去)
答:羊圈的边长AB和BC的长个是20m,20m.
如图:要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB和BC的长各是多少米?
D
C
B
A
25米
课堂检测
能力提升题
4.如图,要设计一个宽20cm,长为30cm的矩形图案,其中有两横两竖彩条,横竖彩条的宽度之比为2∶3 ,若使所有彩条的面积是原来矩形图案面积的三分之一,应如何设计每个彩条的宽度?
解:设横向彩条的宽度2xcm ,竖彩条的宽度3xcm,依题意得: (20-6x)(30-4x)=400
整理得: 6x2-65x+50=0
解方程得:
课堂检测
拓广探索题
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移能聚零为整关系一同了解,从而列方程
课堂小结
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
课后作业
21.3 实际问题与一元二次方程
第一课时
第二课时
第三课时
第一课时
实际问题与一元二次方程
(1)
返回
传染病,一传十,
十传百… …
【想一想】有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
导入新知
素养目标
1.能根据实际问题中的数量关系,正确列出一元二次方程.
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
列一元二次方程解决实际问题
有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
你能解决这个问题吗?
探究新知
知识点 1
问题1
第2轮
???
小明
1
2
x
第1轮
第1轮传染后人数 x+1
小明
第2轮传染后人数 x(x+1)+x+1
【思考】不要忽视小明的二次传染
探究新知
【分析】设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
根据示意图,列表如下:
解:设每轮传染中平均一个人传染了x个人.
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
列方程 x+1+x(x+1)=121
化简得 x2+2x-120=0
(x-10)(x+12)=0
x1=10, x2=-12(舍)
列方程 x+1+x(x+1)=121
提取公因式 (x+1)(x+1)=121
(x+1)2=121
x+1=±11一定要进行检验
x1=10, x2=-12(舍)
有更简单的方法解这个方程吗?
答:平均一个人传染了________个人.
10
注意:一元二次方程的解有可能不符合题意,所以舍去.
探究新知
【想一想】如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法 以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331人.
第一轮传染后的人数 第二轮传染后的
人数 第三轮传染后的
人数
(1+x)1 (1+x)2
【分析】
第1种做法 以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331人.
(1+x)3
探究新知
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1?x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第n轮
【思考】如果按这样的传染速度,n轮后传染后有多少人患了流感?
(1+x)2
(1+x)n
(1+x)3
经过n轮传染后共有 (1+x)n 人患流感.
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x=
探究新知
例1 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即 x2+x-90=0
解得
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
列一元二次方程解传播问题
素养考点 1
探究新知
1.在分析引例和例1中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
【思考】
探究新知
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
【归纳】
探究新知
电脑勒索病毒的传播非常快,如果开始有6台电脑被感染,经过两轮感染后共有2400台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染x台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得=19 或 =-21 (舍去)
依题意 6+6x+6x (1+x) =2400
6 (1+x)? =2400
巩固练习
变式题1
例2 一个小组若干人,新年互送贺卡,若全组共送贺卡72张,则这个小组共多少人?
解:
设这个小组共x人,
根据题意列方程,得
x(x-1)=72
化简,得 x2-x-72=0
解方程,得 x1=9, x2=-8(舍去)
答:这个小组共9人.
列一元二次方程解相互类问题
素养考点 2
探究新知
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,求全组有多少名同学?
解:全组有x名同学,根据题意,得
x(x-1)=182
解得 x1=14,x2=-13(不合题意,舍去)
答:全组有14名同学.
巩固练习
变式题2
1.(2018?绵阳中考在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )
A.9人 B.10人 C.11人 D.12人
解析 设参加酒会的人数为x人,甲跟乙碰杯与乙跟甲碰杯算一次,根据题意得:
x(x﹣1)=55,整理,得:x2﹣x﹣110=0,
解得:x1=11,x2=﹣10(不合题意,舍去).
连接中考
巩固练习
连接中考
C
解析 设共有x个班级参赛,甲班跟乙班比赛与乙班跟甲班比赛算一次,根据题意得: =15,解得:x1=6,x2=﹣5(不合题意,舍去),则共有6个班级参赛.
连接中考
2.(2018?中考)某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?( )
A.4 B.5 C.6 D.7
巩固练习
C
1.元旦将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A.x2=1980 B. x(x+1)=1980
C. x(x-1)=1980 D.x(x-1)=1980
D
课堂检测
基础巩固题
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)?=73
B
课堂检测
基础巩固题
3.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在一天内,一人平均能传染x人,经过两天传染后128人患上甲肝,则x的值为( )?
A.10 B.9 C.8 D.7
D
课堂检测
基础巩固题
1. 为了宣传环保,小明写了一篇倡议书,决定用微博转发的方式传播,他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发倡议书,每个好友转发倡议书之后,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有111个人参与了传播活动,则n=______.
10
课堂检测
能力提升题
2. 某校初三各班进行篮球比赛(单循环制),每两班之间共比赛了6场,求初三有几个班?
解:初三有x个班,根据题意列方程,得
化简,得 x2-x-12=0
解方程,得 x1=4, x2=-3(舍去)
答:初三有4个班.
课堂检测
分析:设每轮分裂中平均每个有益菌可分裂出x个有益菌
60
60x
60(1+x)
60(1+x)
60(1+x)x
3. 某生物实验室需培育一群有益菌,现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
(1)每轮分裂中平均每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
课堂检测
传染源 本轮分裂成有益菌数目 本轮结束有益菌总数
第一轮
第二轮
第三轮
解:设每个有益菌一次分裂出x个有益菌
60+60x+60(1+x)x=24000
x1=19,x2=-21(舍去)
因此每个有益菌一次分裂出19个有益菌.
三轮后有益菌总数为 24000×(1+19)=480000.
课堂检测
解:设每天平均一个人传染了x人,
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2187,
(1+x)7= (1+2)7=2187.
课堂检测
4. 甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同:审题、设元、列方程、解方程、检验、作答.不同的地方是要检验根的合理性.
传播问题
数量关系:
第一轮传播后的量=传播前的量×(1+传播速度)
第二轮传播后的量=第一轮传播后的量×(1+传播速度)=传播前的量×(1+传播速度)2
数字问题
相互问题1
相互问题2
关键要设数位上的数字,要准确地表示出原数.
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2.
甲送乙照片与乙送甲照片是要两张照片,故总数不要除以2.
步骤
类型
课堂小结
第二课时
实际问题与一元二次方程
(2)
返回
【想一想】两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【思考】有关增长/下降率问题,应该如何解答呢?
导入新知
素养目标
1. 能正确列出关于增长率问题的一元二次方程.
2. 通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
有关增长/下降率的问题
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【思考】下降率是什么意思?它与原成本、终成本之间有何数量关系?
探究新知
知识点 1
问题1
【分析】甲种药品成本的年平均下降额为
乙种药品成本的年平均下降额为
乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率.
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为 元,两年后甲种药品成本为 元,
5000(1-x)
5000(1-x)2
依题意得 :5000(1-x)? =3000
解方程,得:
答:甲种药品成本的年平均下降率约22.5%.
探究新知
设乙种药品成本的年平均下降率为y,
一年后乙种药品成本为 元,
两年后乙种药品成本为 元
依题意得, ,
解方程得 ,
6000(1-y)
6000(1-y)2
6000(1-y)2=3600
答:乙种药品成本的年平均下降率约为 .
y1≈0.225,y1≈-1.775
22.5%
探究新知
【思考】为什么选择22.5%作为答案?比较两种药品成本的年平均下降率.经过计算,你能得出什么结论?成本下降额较大的药品,它的成本下降率一定也较大吗?应怎样全面地比较对象的变化状况?
答:经过计算,甲乙两种药品的平均下降率相同 .成本下降额较大的药品,它的成本下降率不一定较大,应比较降前及降后的价格.
探究新知
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的量是a,增长(或降低)n次后的量是A,则它们的数量关系可表示为
其中增长取“+”,降低取“-”
探究新知
【归纳】
=A
例4 某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
列一元二次方程解答增长率问题
素养考点 1
探究新知
某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.求平均每次降价的百分率?
解:设平均每次降价的百分率为x,根据题意得:
36(1- x )2=25
解得
答:平均每次约降价16.7%.
巩固练习
变式题1
1.(2018?中考)某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )
A.80(1+x)2=100 B.100(1﹣x)2=80
C.80(1+2x)=100 D.80(1+x2)=100
解析 由题意知,蔬菜产量的年平均增长率为x,根据2016年蔬菜产量为80吨,则2017年蔬菜产量为80(1+x)吨,2018年蔬菜产量为80(1+x)(1+x)吨,预计2018年蔬菜产量达到100吨,即:80(1+x)(1+x)=100或80(1+x)2=100.
A
巩固练习
连接中考
2.(2018?中考)某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
A.2% B.4.4% C.20% D.44%
解析 设该市2018年、2019年“竹文化”旅游收入的年平均增长率为x,根据题意得:2(1+x)2=2.88,解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
C
巩固练习
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720
C.500(1+x2)=720 D.720(1+x)2=500
B
课堂检测
基础巩固题
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为
课堂检测
2(1+x)+2(1+x)2=8
基础巩固题
受益于国家支持新能源汽车发展和“一带一路”倡议等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计:2014年利润为2亿元,2016年利润为2.88亿元.
(1)求该企业从2014年到2016年的平均增长率.
(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?
解:(1)设年平均增长率为x,依题意得:(2+x)2=2.88.
(2)该企业2017年的利润为2.88×(1+20%)=3.456(亿元).
因为3.456>3.4.
所以该企业2017年的利润能否超过3.4亿元.
课堂检测
能力提升题
某电脑公司2001年的各项经营,一月份的营业额为200万元,一、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率。
分析:设这个增长率为x,一月份的营业额200万元,二月份的营业额是 万元、三月份的营业额 万元,由三月份的总营业额列出等量关系.
200(1+x)
200(1+x)2
解:设平均增长率为x,得
200 + 200(1+x) + 200(1+x)2 = 950
整理,得
200x2 + 600x = 350
解得 x1≈0.5,x2≈-3.5(舍去)
答:这个增长率是50%。
拓广探索题
课堂检测
增长(下降)率问题
增长率问题
下降率问题
基数为a,平均增长/下降率为x
第一次增长
第二次增长
第n次增长
第一次下降
第二次下降
第n次下降
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
a(1±x)n
课堂小结
第三课时
实际问题与一元二次方程
(3)
返回
【思考】通过上节课的学习,请谈谈列方程解应用题的一般步骤是怎样的?关键是什么?
步骤:①审题;②设元;③列式;④解答;⑤验根;⑥答案.
导入新知
【思考】现有长19cm,宽为15cm长方形硬纸片,将它的四角各剪去一个同样大小的正方形后,再折成一个无盖的长方形纸盒,要使纸盒的底面积为77cm?,问剪去的小正方形的边长应是多少?
解:设剪去的小正方形的边长为xcm,则纸盒的长为(19-2x),宽为(15-2x)cm,依题意得(19-2x)(15-2x)=77 ;
整理得:x?-17x+52=0;
解方程,得:(x-13)(x-4)=0;
解得:x1=4,x2=13(舍去);
因此剪去的小正方形的边长应为3cm.
导入新知
素养目标
1.能正确利用面积关系列出关于几何图形的一元二次方程.
2.进一步深入体会一元二次方程在实际生活中的应 用,经历将实际问题转化为数学问题的过程,提 高数学应用意识.
几何图形的面积问题
广东省怀集县马宁镇初级中学 徐志才
如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?
27cm
21cm
探究新知
知识点 1
问题1
广东省怀集县马宁镇初级中学 徐志才
解法一:依据题意知,中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意得:中央矩形的长为 cm,宽为 cm.
因为四周的彩色边衬所点面积是封面面积的______,则中央矩形的面积是封面面积的____.
(27-18x)
(21-14x)
所以可列方程得: (27-18x)(21-14x) = ×27×21
整理,得 16x2-48x+9=0
解方程,得 x= ,x1≈2.8cm,x2≈0.2
所以,9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm
因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.
探究新知
解法二:设正中央的矩形两边分别为9xcm,7xcm,
列方程得:
解得 x 2.6
上、下的边衬的宽为(27-9 2.6) 0.5=1.8cm
左、右的边衬的宽为(21-7 2.6) 0.5=1.4cm
探究新知
例1 有一张长6尺,宽3尺的长方形桌子,现用一块长方形台布铺在桌面上,如果台布的面积是桌面面积的2倍,且四周垂下的长度相同,试求这块台布的长和宽各是多少?(精确到0.1尺)
解:设四周垂下的宽度为x尺时,则台布的长为(2x+6)尺,宽为(2x+3)尺,依题意得:(6+2x)(3+2x)=2×6×3
整理方程得:2x?+9x-9=0
解得:x1≈0.84,x2≈-5.3(不合题意,舍去)
因此:台布的长为:2×0.84+6≈7.7(尺)
台布的宽为:2×0.84+3≈4.7(尺)
即这块台布的长约为7.7尺,宽约为4.7尺.
利用一元二次方程解答一般面积问题
素养考点 1
探究新知
变式题1
要为一幅长29cm,宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框的宽度应是多少厘米(结果保留小数点后一位)?
解:设镜框的宽为xcm,根据题意,得
整理得8x2+204x-319=0,解得 .
∴x1= ,x2= (不合题意,舍去). ∴x= ≈1.5.
答:镜框的宽度约为1.5cm.
巩固练习
例2 如右图是长方形鸡场的平面示意图。一边靠墙,另三边用竹篱笆围成,且竹篱笆总长为35m。
(1)若所围的面积为150m?,试求此长方形鸡场的长和宽;
A
B
C
D
解:设BC=xcm,则AB=CD= (35-x),依题意可列方程:
(35-x)x=150.整理得:x2-35x+300=0,
解方程,得(x-20)(x-15)=0
即:x1=20,x2=15. 当BC=x=20m时,AB=CD=7.5m,
当BC=15m时,AB=CD=10m,即这个长方形鸡场的长与
宽分别为20m和7.5m或15m和10m。
靠墙问题的解答
素养考点 2
探究新知
(2)如果墙长为18m,则(1)中长方形鸡场的长和宽分别是多少?
解:当墙长为18m时,显然BC=20m时,所围成的鸡场会在靠墙处留下一个缺口,不合题意,应舍去,此时所围成的长方形鸡场的长与宽值能是15m和10m.
点拨:在寻找关系式时,切记三边之和等于总长,而不是四边之和等于总长.
探究新知
(3)能围成面积为160m?的长方形鸡场吗?说说你的理由。
解:不能围成面积为160m?的长方形鸡场,理由如下:
设BC=xm,由(1)知AB=(35-x),从而有(35-x)x=160,方程整理为x?-35x+320=0.此时Δ=35?-4×1×320=-55<0,原方程没有实数根,从而知用35m的篱笆按图示方式不能围成面积为160m?的鸡场。
探究新知
变式题2 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80平方米?
住房墙
1m
解:设矩形猪舍垂直于住房墙的一边长为x m,
由题意得 x(25-2x+1)=80
整理,得 x2-13x+40=0
解方程,得 (x-5)(x-8)=0
即: x1=5 , x2=8
当x=5时,26-2x=16>12 (舍去);当x=8时,26-2x=10<12
故所围矩形猪舍的长为10m,宽为8m.
则平行于住房墙的一边长(25-2x+1)m.
巩固练习
20
32
x
x
解:设道路的宽为x米,依题意得
例3 如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
还有其他方法吗?
修路问题的图形面积
20×32-32x-20x+x2=540
素养考点 3
探究新知
解:设道路的宽为 x 米
20
32
x
x
20-x
32-x
(32-x)(20-x)=540
整理,得x2-52x+100=0
解方程,得(x-50)(x-2)=0
即 x1=2,x2=50
当x=50时,32-x=-18,不合题意,舍去.
∴取x=2
答:道路的宽为2米.
方法二
探究新知
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540㎡,求这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-x)(20-x)=540
可列方程为
变式一
探究新知
20
32
x
x
x
20-x
如图,在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-x)=540
可列方程为
变式二
32-2x
探究新知
20
32
x
x
x
x
20
32
2x
2x
32-2x
20-2x
如图,在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-2x)=540
可列方程为
变式三
探究新知
在宽为20m, 长为32m的矩形地面上修筑四条道路,余下的部分种上草坪,如果横、纵小路的宽度比为3:2,且使小路所占面积是矩形面积的四分之一,求道路的宽为多少?
变式四
探究新知
小路所占面积是矩形面积的四分之一
剩余面积是矩形面积的四分之三
解:设横、竖小路的宽度分别为3x、 2x,
于是可列方程
(30-4x)(20-6x)= —×20×30
20㎝
30㎝
3x
2x
30-4x
20-6x
4
3
3x
2x
6x
4x
30-4x
20-6x
探究新知
我们利用“图形经过移动,它的面积大小不会改变”的性质,把纵、横两条路移动一下,使列方程容易些(目的是求出结果,至于实际施工,仍可按原图的位置进行).
方法点拨
探究新知
如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
巩固练习
变式题3
解:设道路宽为x米,
依题意得
整理得,x2-36x+35=0
其中的 x=35超出了原矩形的宽,应舍去.
答:道路的宽为1米.
(32-2x)(20-x)=570
解方程,得(x-35)(x-1)=0
即:x1=35,x2=1
巩固练习
(2018?中考)公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
A.(x+1)(x+2)=18 B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18 D.x2+3x+16=0
解析 设原正方形的边长为xm,依题意有
(x﹣1)(x﹣2)=18,故选C.
巩固练习
连接中考
C
1. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
80cm
x
x
x
x
50cm
B
课堂检测
基础巩固题
2.一块长方形铁板,长是宽的2倍,如果在4个角上截去边长为5cm的小正方形,然后把四边折起来,做成一个没有盖的盒子,盒子的容积是3000 cm3,求铁板的长和宽.
解:设铁板的宽为x cm,则有长为2x cm,依题意得:
5(2x-10)(x-10)=3000; 整理得:x2-15x-250=0;
解方程,得:(x-25)(x+10)=0;
即: x1=25 x2=-10(舍去);所以 2x=50
答:铁板的长50cm,宽为25cm.
课堂检测
解:设AB长是x m,依题意得: (100-4x)x=400
整理得:x2-25x+100=0
解方程得:(x-20)(x-5)=0
即 x1=5,x2=20
x=20,100-4x=20<25 ; x=5,100-4x=80>25 x=5(舍去)
答:羊圈的边长AB和BC的长个是20m,20m.
如图:要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB和BC的长各是多少米?
D
C
B
A
25米
课堂检测
能力提升题
4.如图,要设计一个宽20cm,长为30cm的矩形图案,其中有两横两竖彩条,横竖彩条的宽度之比为2∶3 ,若使所有彩条的面积是原来矩形图案面积的三分之一,应如何设计每个彩条的宽度?
解:设横向彩条的宽度2xcm ,竖彩条的宽度3xcm,依题意得: (20-6x)(30-4x)=400
整理得: 6x2-65x+50=0
解方程得:
课堂检测
拓广探索题
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移能聚零为整关系一同了解,从而列方程
课堂小结
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
课后作业
同课章节目录
