22.1.4二次函数y=ax2+bx+c的图像和性质课件(共2课时,58张PPT)
文档属性
| 名称 | 22.1.4二次函数y=ax2+bx+c的图像和性质课件(共2课时,58张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 23:22:05 | ||
图片预览








文档简介
九年级数学上册
22.1 二次函数图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第一课时
第二课时
第一课时
返回
22.1.4 二次函数y=ax2+bx+c的
图象和性质(1)
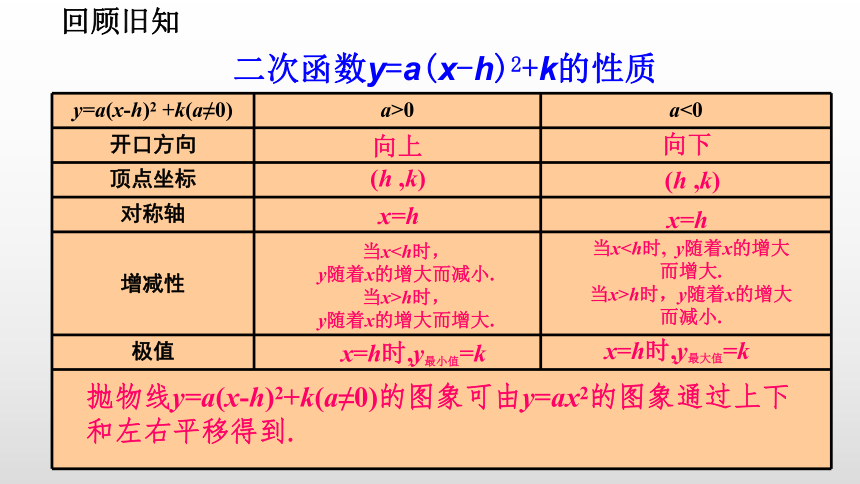
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当xy随着x的增大而减小.
当x>h时,
y随着x的增大而增大.
当x当x>h时,y随着x的增大而减小.
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
回顾旧知
二次函数y=a(x-h)2+k的性质
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数y=ax2+bx+c 图象和性质?
导入新知
素养目标
3. 能根据所给的自变量的取值范围画二次函数的图象.
1. 会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2. 能熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.
画出二次函数y=ax2+bx+c的图象
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
【思考1】怎样将 化成y=a(x-h)2+k的形式?
探究新知
知识点 1
配方可得
想一想:配方的方法及步骤是什么?
探究新知
怎样将 化成y=a(x-h)2+k的形式?
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
【提示】配方后的表达式通常称为配方式或顶点式.
探究新知
【思考2】你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
【思考3】二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
探究新知
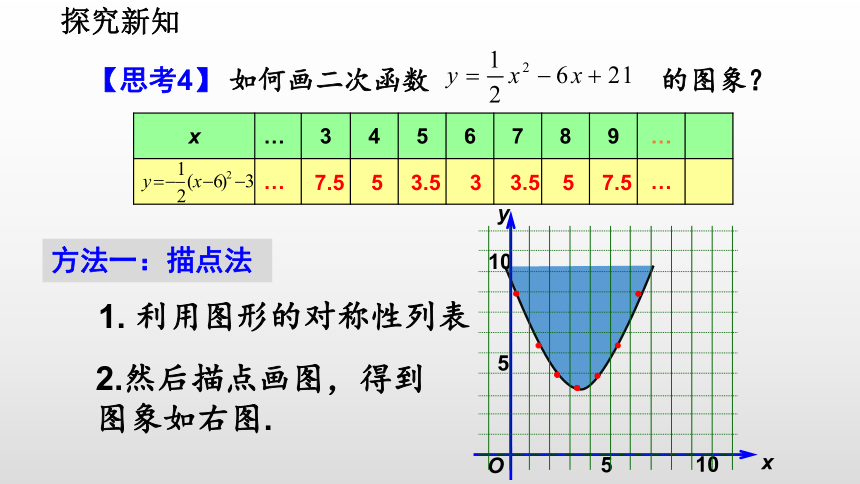
【思考4】 如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
1. 利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
2.然后描点画图,得到
图象如右图.
O
方法一:描点法
探究新知
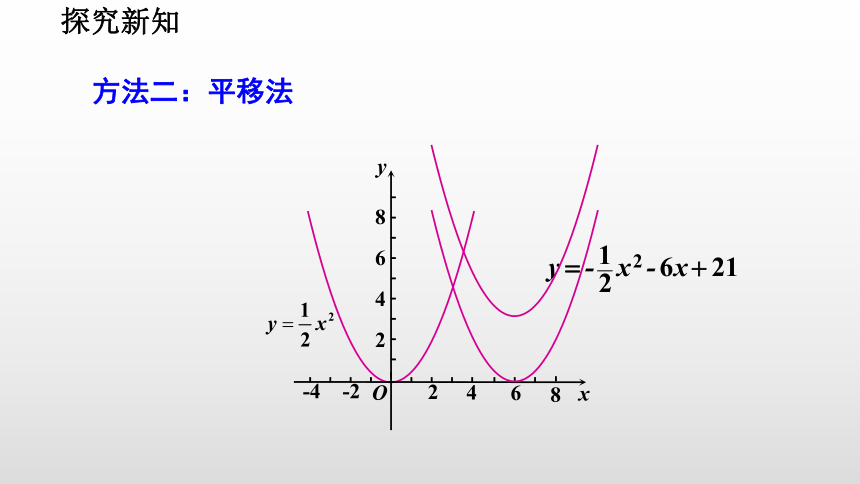
方法二:平移法
2
6
8
y
4
O
-2
2
x
4
-4
6
8
探究新知
2
6
8
y
4
O
-2
2
x
4
-4
6
8
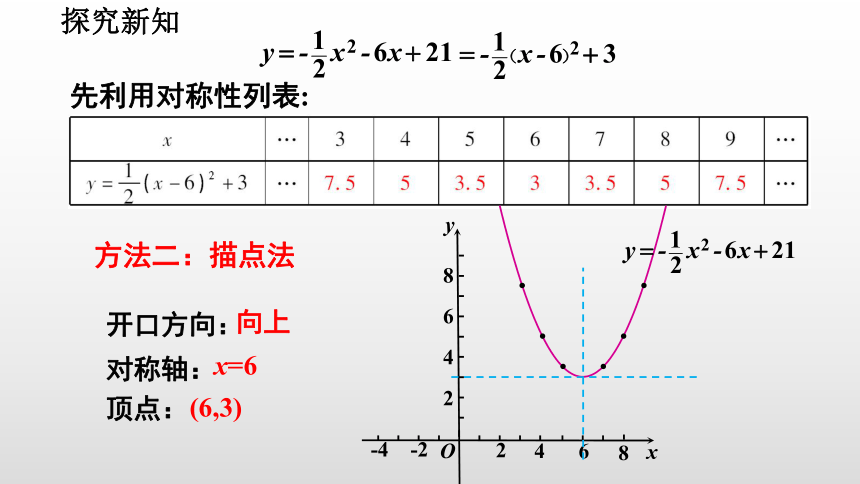
方法二:描点法
先利用对称性列表:
开口方向:
对称轴:
顶点:
向上
x=6
(6,3)
探究新知
【思考4】 结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
探究新知
开口方向:
对称轴:
顶点:
向上
x=6
(6,3)
例1 画出函数 的图象,并说明这个函数具有哪些性质.
x ··· -2 -1 0 1 2 3 4 ···
y ··· ···
-6.5
-4
-2.5
-2
-2.5
-4
-6.5
解: 函数 通过配方可得 ,
先列表:
画二次函数y=ax2+bx+c的图象并且说出它的性质
素养考点 1
探究新知
2
x
y
-2
0
4
-2
-4
-4
-6
-8
然后描点、连线,得到图象如下图:
由图象可知,这个函数具有如下性质:
开口方向:向下
顶点坐标:(1,-2)
对称轴:x=1
最值:x=1时,y最大值=-2
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
探究新知
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
巩固练习
变式题1
二次函数y=ax2+bx+c 的图象与性质
根据下列关系你能发现二次函数y=ax2+bx+c的图象和性质吗?
y=ax2+bx+c
探究新知
知识点 2
y=ax2+bx+c
二次函数的顶点式
对称轴为 .
二次函数的一般表达式
因此,抛物线的对称轴是 ,顶点是 .
探究新知
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
增减性?
最小值
最大值
探究新知
探究新知
指出二次函数y=ax2+bx+c的有关性质
例2 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
解析 ∵二次函数y=x2+2x﹣3的二次项系数为a=1>0,
∴函数图象开口向上,
∵y=x?+2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
方法点拨:把函数的一般式化为顶点式,再由定点式确定开口方向、对称轴、顶点及其他性质.
素养考点 2
A
探究新知
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
填一填.
巩固练习
变式题2
二次函数字母系数与图象的关系
一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:
x
y
O
y=k1x+b1
x
y
O
y=k2x+b2
y=k3x+b3
k1 ___ 0
b1 ___ 0
k2 ___ 0
b2 ___ 0
>
>
<
k3 ___ 0
b3 ___ 0
<
>
探究新知
知识点 3
>
x
y
O
二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,x<0
对称轴在y轴右侧,x>0
x=0时,y=c.
探究新知
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
x=0时,y=c.
探究新知
字母符号 图象的特征
a>0 开口_____________
a<0 开口_____________
b=0 对称轴为_____轴
a、b同号 对称轴在y轴的____侧
a、b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
探究新知
二次函数y=ax2+bx+c的图象与a、b、c的关系
例3 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0, 故③正确;
由图可知x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;
由对称轴x>-1可得2a-b<0,故②正确;
利用二次函数y=ax2+bx+c的图象确定字母的值
素养考点 3
探究新知
变式题3
二次函数y=ax?+bx+c的图象如图所示,下列选项中正确的是( )
A.a>0 B.b>0 C.c<0 D. ac>0
巩固练习
解析 根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号.
①∵开口向下,∴a<0,A错误;②对称轴在y轴的右侧和a<0,可知b>0,B正确;③抛物线与y轴交于正半轴,c>0,C错误;④因为a<0,c>0,所以ac<0,D错误.
B
(2018?中考)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
解析 由图象开口向下,可知a<0,有对称轴在y轴右侧,可知b>0,即ab<0,故①正确,由对称轴x=1得: =1,即2a+b=0,故②正确,当x=3时,y<0,即9a+3b+c<0,∵b=-2a,∴3a+c<0,故③不正确,当x=1时,函数有最大值a+b+c,当x=m时,y=am2+bm+c,即a+b+c≥am2+bm+c,也就是a+b≥m(am+b),故④正确,由图象知:当-1<x<3时,y有可能小于0,故⑤不正确.
巩固练习
A
连接中考
1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A. y轴 B.直线x=
C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
课堂检测
基础巩固题
O
y
x
–1
–2
3
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;(2)当x=–1和x=3时,函数值相等;
(3) 4a+b=0; (4)当y=–2时,x的值只能取0;
其中正确的是 .
(2)
课堂检测
基础巩固题
3. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则y1>y2.其中正确
的是( )
A.①②③ B.①③④
C.①②④ D.②③④
x
y
O
2
x=-1
B
课堂检测
基础巩固题
根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
课堂检测
能力提升题
1.已知函数y=-2x2+x-4,当x= 时,y有最大值 .
2.已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
课堂检测
拓广探索题
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
课堂小结
第二课时
返回
22.1.4 二次函数y=ax2+bx+c的
图象和性质(2)
用待定系数法求函数的解析式
已知一次函数经过点(1,3)和(-2,-12),求这个一次函数的解析式。
解:设这个一次函数的解析式为y=kx+b,因为一次函数经过点(1,3)和(-2,-12),
所以
解得 k=3,b=-6
一次函数的解析式为y=3x-6.
【思考】如何用待定系数法求二次函数的解析式呢?
回顾旧知
素养目标
2.灵活应用三点式、顶点式、交点式求二次函数的解析式.
1.会用待定系数法求二次函数的解析式.
【思考】回忆一下用待定系数法求一次函数的解析式的一般步骤.求二次函数y=ax2+bx+c的解析式的关键是什么?
用三点式求二次函数的解析式
探究新知
知识点 1
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式。对于二次函数,由几个点的坐标可以确定二次函数?
已知一个二次函数的图象过点(-1,10)、(1,4),求这个函数的解析式.
解:
设所求的二次函数为y=ax2+bx+c.
由已知得:
a-b+c=10
a+b+c=4
三个未知数,两个等量关系,这个方程组能解吗?
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组。
探究新知
已知一个二次函数的图象过点(-1,10)、(1,4) 、(2,7),求这个函数的解析式.
第一步:设出解析式的 形式;
第二步:代入已知点的 坐标;
第三步:解方程组。
解:
设所求的二次函数为y=ax2+bx+c.
由已知得:
a-b+c=10
a+b+c=4
4a+2b+c=7
三个未知数,三个等量关系,这个方程组能解吗?
探究新知
a-b+c=10
a+b+c=4
4a+2b+c=7
①
②
③
?
由②-①可得:
2b=-6
b=-3
由③-①可得:
3a+3b=-3
a+b=-1
a=2
将a=2,b=-3代入①可得:
2+3+c=10
c=5
∴解方程组得:
a=2, b=-3, c=5.
探究新知
例1 已知一个二次函数的图象过点A(-1,0), B(4,5), C(0,-3). 三点,求这个函数的解析式.
解:设所求抛物线的解析式为y=ax2+bx+c.
∵抛物线经过点A(-1,0), B(4,5), C(0,-3).
∴
解得a=1,b=-2,c=-3.
∴抛物线的解析式为y=x2-2x-3.
利用三点式求二次函数的解析式
素养考点 1
探究新知
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值。
若已知条件是二次函数图像上三个点的坐标,可设解析式为y=ax2+bx+c,列出关于a,b,c的方程组,并求出a,b,c,就可以写出二次函数的解析式。
归纳
任意两点的连线不与y轴平行
三点式求二次函数的解析式
探究新知
已知一个二次函数的图象过点A(0,0), B(-1,-1), C(1,9)三点,求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组。
解:设所求抛物线的解析式为y=ax2+bx+c.
∵抛物线经过点A(0,0), B(-1,-1), C(1,9).
∴
解得a=4,b=5,c=0.
∴抛物线的解析式为y=4x2+5x.
0=c
-1=a-b+c
9=a+b+c
巩固练习
变式题1
用交点式y=a(x-x1) (x-x2) 求二次函数解析式
一个二次函数,当自变量x=0时,函数值y=-1,当x=-2与 时,y=0,求这个二次函数的解析式.
探究新知
知识点 2
两种方法的结果一样吗?两种方法哪一个更简捷?
交点式求二次函数的解析式:若已知抛物线与x轴的两交点坐标,可设解析式为y=a(x-x1)(x-x2),把另一点的坐标代入,解关于a的一元一次方程.
例2 已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点(两点的纵坐标都为0),与y轴交于点C(0,3),求这个二次函数的解析式.
解: ∵图象与x轴交于A(1,0),B(3,0)
∴设函数解析式为y=a(x-1)(x-3)
∵图象过点C(0,3)
∴3=a(0-1)(0-3),解得a=1.
∴二次函数解析式为y=(x-1)(x-3)=x2-4x+3
利用交点式求二次函数的解析式
素养考点 2
探究新知
已知抛物线与x轴交于A(-1,0),
B(1,0)并经过点M(0,1),求抛物线的解析式.
因此所求的抛物线解析式为
y=-x2+1.
解: ∵图象与x轴交于A(-1,0),B(1,0)
∴设函数解析式为y=a(x+1)(x-1)
∵图象过点M(0,1)
∴1=a(0+1)(0-1),解得a=-1.
∴二次函数解析式为y=-1(x+1)(x-1)
巩固练习
变式题 2
【思考】图象顶点为(h, k)的二次函数的解析式是y=a(x-h)2+k,如果顶点坐标已知,那么求解析式的关键是什么?
用二次函数顶点式y=a(x-h)2+k求函数解析式
探究新知
知识点 3
利用顶点式求二次函数的解析式
例3 已知抛物线顶点为(1,-4),且又过点(2,-3),求其解析式.
解:∵抛物线顶点为(1,-4)
∴设其解析式为y=a(x-1)2-4, 又抛物线过点(2,-3),
则-3=a(2-1)2-4,则a=1.
∴其解析式为y=(x-1)2-4=x2-2x-3.
探究新知
素养考点 3
若已知顶点坐标和一点,可设解析式为y=a(x-h)2+k,将另一点坐标代入解关于a的一元一次方程.
归纳
顶点式求二次函数的解析式
探究新知
变式题3
已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),求这个二次函数的关系式.
解:∵抛物线顶点为(-1,2)
∴设其解析式为y=a(x+1)2+2,
又抛物线过点(1,-3),
则3=a(1+1)2+2,则a= .
所以这个二次函数的关系式是y= (x+1)2+2.
巩固练习
(2018?中考)已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5),求该函数的关系式.
解:设抛物线顶点式y=a(x+1)2+4
将B(2,﹣5)代入得:a=﹣1
∴该函数的解析式为:y=﹣(x+1)2+4
y=﹣x2﹣2x+3
连接中考
巩固练习
连接中考
1. 如图所示,在平面直角坐标系中,二次函数y=ax2+bx+c的图象顶点为A(-2,-2),且过点B(0,2),则y与x的函数关系式为( )
A. y=x2+2 B. y=(x-2)2+2
C. y=(x-2)2-2 D. y=(x+2)2-2
2. 已知二次函数的图象经过点(4,-3),并且当x=3时有最大值4,则其解析式为 .
D
y=-7(x-3)2+4.
课堂检测
基础巩固题
如图所示,已知抛物线的对称轴是直线x=3,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(8,0)、(0,4),求这个抛物线的解析式.
解:由抛物线过A(8,0)及对称轴为x=3,
知抛物线一定过点(-2,0).
设这个抛物线的解析式为y=a(x+2)(x-8),
∵抛物线过点(0,4),
∴4=a(0+2)(0-8),
课堂检测
能力提升题
已知抛物线顶点(1,16),且抛物线与x轴的两交点间的距离为8,求其解析式.
解:由题意可知抛物线与x轴交点坐标为(5,0),(-3,0),
设解析式为y=a(x-5)(x+3),
∵抛物线过点(1,16)
∴16=a(1-5)(1+3),解得a=-1.
∴抛物线的解析式为y=-(x-5)(x+3)=-x2+2x+15.
课堂检测
拓广探索题
待定系数法求二次函数的解析式
三点式
交点式
顶点式
已知抛物线上三个点的坐标,设解析式为 y=ax2+bx+c
已知抛物线与x轴两交点的坐标,设解析式为 y=(x-x1)(x-x2)
已知抛物线顶点坐标和另一个点的坐标,设解析式为
y=a(x-h)2+k
课堂小结
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
课后作业
22.1 二次函数图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第一课时
第二课时
第一课时
返回
22.1.4 二次函数y=ax2+bx+c的
图象和性质(1)
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
当x>h时,
y随着x的增大而增大.
当x
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
回顾旧知
二次函数y=a(x-h)2+k的性质
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数y=ax2+bx+c 图象和性质?
导入新知
素养目标
3. 能根据所给的自变量的取值范围画二次函数的图象.
1. 会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2. 能熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.
画出二次函数y=ax2+bx+c的图象
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
【思考1】怎样将 化成y=a(x-h)2+k的形式?
探究新知
知识点 1
配方可得
想一想:配方的方法及步骤是什么?
探究新知
怎样将 化成y=a(x-h)2+k的形式?
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
【提示】配方后的表达式通常称为配方式或顶点式.
探究新知
【思考2】你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
【思考3】二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
探究新知
【思考4】 如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
1. 利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
2.然后描点画图,得到
图象如右图.
O
方法一:描点法
探究新知
方法二:平移法
2
6
8
y
4
O
-2
2
x
4
-4
6
8
探究新知
2
6
8
y
4
O
-2
2
x
4
-4
6
8
方法二:描点法
先利用对称性列表:
开口方向:
对称轴:
顶点:
向上
x=6
(6,3)
探究新知
【思考4】 结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
探究新知
开口方向:
对称轴:
顶点:
向上
x=6
(6,3)
例1 画出函数 的图象,并说明这个函数具有哪些性质.
x ··· -2 -1 0 1 2 3 4 ···
y ··· ···
-6.5
-4
-2.5
-2
-2.5
-4
-6.5
解: 函数 通过配方可得 ,
先列表:
画二次函数y=ax2+bx+c的图象并且说出它的性质
素养考点 1
探究新知
2
x
y
-2
0
4
-2
-4
-4
-6
-8
然后描点、连线,得到图象如下图:
由图象可知,这个函数具有如下性质:
开口方向:向下
顶点坐标:(1,-2)
对称轴:x=1
最值:x=1时,y最大值=-2
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
探究新知
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
巩固练习
变式题1
二次函数y=ax2+bx+c 的图象与性质
根据下列关系你能发现二次函数y=ax2+bx+c的图象和性质吗?
y=ax2+bx+c
探究新知
知识点 2
y=ax2+bx+c
二次函数的顶点式
对称轴为 .
二次函数的一般表达式
因此,抛物线的对称轴是 ,顶点是 .
探究新知
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
增减性?
最小值
最大值
探究新知
探究新知
指出二次函数y=ax2+bx+c的有关性质
例2 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
解析 ∵二次函数y=x2+2x﹣3的二次项系数为a=1>0,
∴函数图象开口向上,
∵y=x?+2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
方法点拨:把函数的一般式化为顶点式,再由定点式确定开口方向、对称轴、顶点及其他性质.
素养考点 2
A
探究新知
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,-6)
直线x=
填一填.
巩固练习
变式题2
二次函数字母系数与图象的关系
一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:
x
y
O
y=k1x+b1
x
y
O
y=k2x+b2
y=k3x+b3
k1 ___ 0
b1 ___ 0
k2 ___ 0
b2 ___ 0
>
>
<
k3 ___ 0
b3 ___ 0
<
>
探究新知
知识点 3
>
x
y
O
二次函数 的图象如下图所示,请根据二次函数的性质填空:
a1 ___ 0
b1___ 0
c1___ 0
a2___ 0
b2___ 0
c2___ 0
>
>
>
>
<
=
开口向上,a>0
对称轴在y轴左侧,x<0
对称轴在y轴右侧,x>0
x=0时,y=c.
探究新知
x
y
O
a3___ 0
b3___ 0
c3___ 0
a4___ 0
b4___ 0
c4___ 0
<
=
>
<
>
<
开口向下,a<0
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
x=0时,y=c.
探究新知
字母符号 图象的特征
a>0 开口_____________
a<0 开口_____________
b=0 对称轴为_____轴
a、b同号 对称轴在y轴的____侧
a、b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
探究新知
二次函数y=ax2+bx+c的图象与a、b、c的关系
例3 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0, 故③正确;
由图可知x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;
由对称轴x>-1可得2a-b<0,故②正确;
利用二次函数y=ax2+bx+c的图象确定字母的值
素养考点 3
探究新知
变式题3
二次函数y=ax?+bx+c的图象如图所示,下列选项中正确的是( )
A.a>0 B.b>0 C.c<0 D. ac>0
巩固练习
解析 根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号.
①∵开口向下,∴a<0,A错误;②对称轴在y轴的右侧和a<0,可知b>0,B正确;③抛物线与y轴交于正半轴,c>0,C错误;④因为a<0,c>0,所以ac<0,D错误.
B
(2018?中考)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
解析 由图象开口向下,可知a<0,有对称轴在y轴右侧,可知b>0,即ab<0,故①正确,由对称轴x=1得: =1,即2a+b=0,故②正确,当x=3时,y<0,即9a+3b+c<0,∵b=-2a,∴3a+c<0,故③不正确,当x=1时,函数有最大值a+b+c,当x=m时,y=am2+bm+c,即a+b+c≥am2+bm+c,也就是a+b≥m(am+b),故④正确,由图象知:当-1<x<3时,y有可能小于0,故⑤不正确.
巩固练习
A
连接中考
1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A. y轴 B.直线x=
C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
课堂检测
基础巩固题
O
y
x
–1
–2
3
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;(2)当x=–1和x=3时,函数值相等;
(3) 4a+b=0; (4)当y=–2时,x的值只能取0;
其中正确的是 .
(2)
课堂检测
基础巩固题
3. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则y1>y2.其中正确
的是( )
A.①②③ B.①③④
C.①②④ D.②③④
x
y
O
2
x=-1
B
课堂检测
基础巩固题
根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
课堂检测
能力提升题
1.已知函数y=-2x2+x-4,当x= 时,y有最大值 .
2.已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
课堂检测
拓广探索题
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
课堂小结
第二课时
返回
22.1.4 二次函数y=ax2+bx+c的
图象和性质(2)
用待定系数法求函数的解析式
已知一次函数经过点(1,3)和(-2,-12),求这个一次函数的解析式。
解:设这个一次函数的解析式为y=kx+b,因为一次函数经过点(1,3)和(-2,-12),
所以
解得 k=3,b=-6
一次函数的解析式为y=3x-6.
【思考】如何用待定系数法求二次函数的解析式呢?
回顾旧知
素养目标
2.灵活应用三点式、顶点式、交点式求二次函数的解析式.
1.会用待定系数法求二次函数的解析式.
【思考】回忆一下用待定系数法求一次函数的解析式的一般步骤.求二次函数y=ax2+bx+c的解析式的关键是什么?
用三点式求二次函数的解析式
探究新知
知识点 1
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式。对于二次函数,由几个点的坐标可以确定二次函数?
已知一个二次函数的图象过点(-1,10)、(1,4),求这个函数的解析式.
解:
设所求的二次函数为y=ax2+bx+c.
由已知得:
a-b+c=10
a+b+c=4
三个未知数,两个等量关系,这个方程组能解吗?
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组。
探究新知
已知一个二次函数的图象过点(-1,10)、(1,4) 、(2,7),求这个函数的解析式.
第一步:设出解析式的 形式;
第二步:代入已知点的 坐标;
第三步:解方程组。
解:
设所求的二次函数为y=ax2+bx+c.
由已知得:
a-b+c=10
a+b+c=4
4a+2b+c=7
三个未知数,三个等量关系,这个方程组能解吗?
探究新知
a-b+c=10
a+b+c=4
4a+2b+c=7
①
②
③
?
由②-①可得:
2b=-6
b=-3
由③-①可得:
3a+3b=-3
a+b=-1
a=2
将a=2,b=-3代入①可得:
2+3+c=10
c=5
∴解方程组得:
a=2, b=-3, c=5.
探究新知
例1 已知一个二次函数的图象过点A(-1,0), B(4,5), C(0,-3). 三点,求这个函数的解析式.
解:设所求抛物线的解析式为y=ax2+bx+c.
∵抛物线经过点A(-1,0), B(4,5), C(0,-3).
∴
解得a=1,b=-2,c=-3.
∴抛物线的解析式为y=x2-2x-3.
利用三点式求二次函数的解析式
素养考点 1
探究新知
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值。
若已知条件是二次函数图像上三个点的坐标,可设解析式为y=ax2+bx+c,列出关于a,b,c的方程组,并求出a,b,c,就可以写出二次函数的解析式。
归纳
任意两点的连线不与y轴平行
三点式求二次函数的解析式
探究新知
已知一个二次函数的图象过点A(0,0), B(-1,-1), C(1,9)三点,求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组。
解:设所求抛物线的解析式为y=ax2+bx+c.
∵抛物线经过点A(0,0), B(-1,-1), C(1,9).
∴
解得a=4,b=5,c=0.
∴抛物线的解析式为y=4x2+5x.
0=c
-1=a-b+c
9=a+b+c
巩固练习
变式题1
用交点式y=a(x-x1) (x-x2) 求二次函数解析式
一个二次函数,当自变量x=0时,函数值y=-1,当x=-2与 时,y=0,求这个二次函数的解析式.
探究新知
知识点 2
两种方法的结果一样吗?两种方法哪一个更简捷?
交点式求二次函数的解析式:若已知抛物线与x轴的两交点坐标,可设解析式为y=a(x-x1)(x-x2),把另一点的坐标代入,解关于a的一元一次方程.
例2 已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点(两点的纵坐标都为0),与y轴交于点C(0,3),求这个二次函数的解析式.
解: ∵图象与x轴交于A(1,0),B(3,0)
∴设函数解析式为y=a(x-1)(x-3)
∵图象过点C(0,3)
∴3=a(0-1)(0-3),解得a=1.
∴二次函数解析式为y=(x-1)(x-3)=x2-4x+3
利用交点式求二次函数的解析式
素养考点 2
探究新知
已知抛物线与x轴交于A(-1,0),
B(1,0)并经过点M(0,1),求抛物线的解析式.
因此所求的抛物线解析式为
y=-x2+1.
解: ∵图象与x轴交于A(-1,0),B(1,0)
∴设函数解析式为y=a(x+1)(x-1)
∵图象过点M(0,1)
∴1=a(0+1)(0-1),解得a=-1.
∴二次函数解析式为y=-1(x+1)(x-1)
巩固练习
变式题 2
【思考】图象顶点为(h, k)的二次函数的解析式是y=a(x-h)2+k,如果顶点坐标已知,那么求解析式的关键是什么?
用二次函数顶点式y=a(x-h)2+k求函数解析式
探究新知
知识点 3
利用顶点式求二次函数的解析式
例3 已知抛物线顶点为(1,-4),且又过点(2,-3),求其解析式.
解:∵抛物线顶点为(1,-4)
∴设其解析式为y=a(x-1)2-4, 又抛物线过点(2,-3),
则-3=a(2-1)2-4,则a=1.
∴其解析式为y=(x-1)2-4=x2-2x-3.
探究新知
素养考点 3
若已知顶点坐标和一点,可设解析式为y=a(x-h)2+k,将另一点坐标代入解关于a的一元一次方程.
归纳
顶点式求二次函数的解析式
探究新知
变式题3
已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),求这个二次函数的关系式.
解:∵抛物线顶点为(-1,2)
∴设其解析式为y=a(x+1)2+2,
又抛物线过点(1,-3),
则3=a(1+1)2+2,则a= .
所以这个二次函数的关系式是y= (x+1)2+2.
巩固练习
(2018?中考)已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5),求该函数的关系式.
解:设抛物线顶点式y=a(x+1)2+4
将B(2,﹣5)代入得:a=﹣1
∴该函数的解析式为:y=﹣(x+1)2+4
y=﹣x2﹣2x+3
连接中考
巩固练习
连接中考
1. 如图所示,在平面直角坐标系中,二次函数y=ax2+bx+c的图象顶点为A(-2,-2),且过点B(0,2),则y与x的函数关系式为( )
A. y=x2+2 B. y=(x-2)2+2
C. y=(x-2)2-2 D. y=(x+2)2-2
2. 已知二次函数的图象经过点(4,-3),并且当x=3时有最大值4,则其解析式为 .
D
y=-7(x-3)2+4.
课堂检测
基础巩固题
如图所示,已知抛物线的对称轴是直线x=3,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(8,0)、(0,4),求这个抛物线的解析式.
解:由抛物线过A(8,0)及对称轴为x=3,
知抛物线一定过点(-2,0).
设这个抛物线的解析式为y=a(x+2)(x-8),
∵抛物线过点(0,4),
∴4=a(0+2)(0-8),
课堂检测
能力提升题
已知抛物线顶点(1,16),且抛物线与x轴的两交点间的距离为8,求其解析式.
解:由题意可知抛物线与x轴交点坐标为(5,0),(-3,0),
设解析式为y=a(x-5)(x+3),
∵抛物线过点(1,16)
∴16=a(1-5)(1+3),解得a=-1.
∴抛物线的解析式为y=-(x-5)(x+3)=-x2+2x+15.
课堂检测
拓广探索题
待定系数法求二次函数的解析式
三点式
交点式
顶点式
已知抛物线上三个点的坐标,设解析式为 y=ax2+bx+c
已知抛物线与x轴两交点的坐标,设解析式为 y=(x-x1)(x-x2)
已知抛物线顶点坐标和另一个点的坐标,设解析式为
y=a(x-h)2+k
课堂小结
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
课后作业
同课章节目录
