苏科版八年级数学下册第11章反比例函数复习题(一)含答案
文档属性
| 名称 | 苏科版八年级数学下册第11章反比例函数复习题(一)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 293.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 20:57:44 | ||
图片预览




文档简介
第11章 反比例函数 第二次月考复习题汇编(一)
一、选择题
1.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
2.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
3.已知点A(m﹣2,y1)、B(m+1,y2)在反比例函数的图象上且y1>y2,则m范围是( )
A.m<-1 B.m>2 C.-1<m<2 D. 无法确定
4.在同一平面直角坐标系中,函数与的图象可能是( )
A. B. C. D.
二、填空题
5.在函数的图象上有三个点(-2,),(-1,),(,),则,,的大小关系为 .
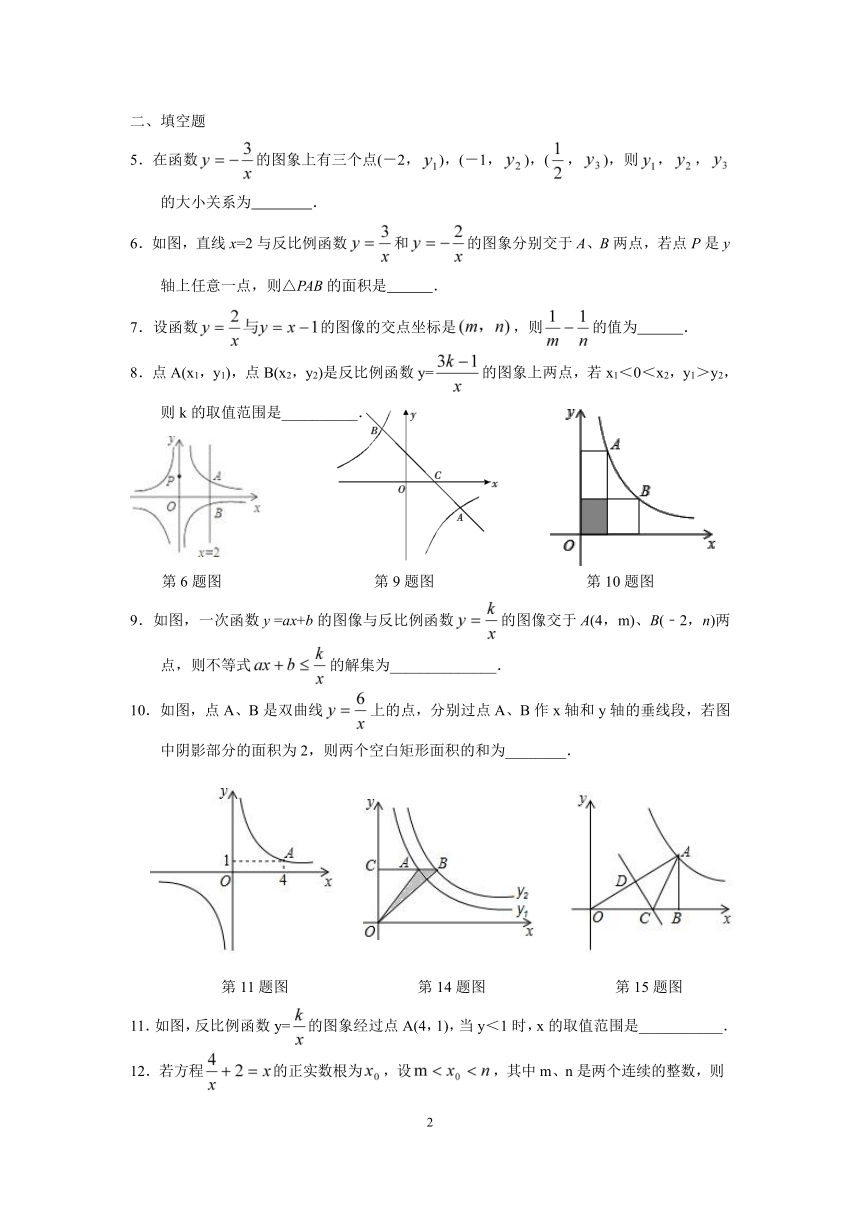
6.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
7.设函数的图像的交点坐标是,则的值为 .
8.点A(x1,y1),点B(x2,y2)是反比例函数y=的图象上两点,若x1<0<x2,y1>y2,则k的取值范围是__________.
第6题图 第9题图 第10题图
9.如图,一次函数y =ax+b的图像与反比例函数的图像交于A(4,m)、B(﹣2,n)两点,则不等式的解集为______________.
10.如图,点A、B是双曲线上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为________.
第11题图 第14题图 第15题图
11.如图,反比例函数y=的图象经过点A(4,1),当y<1时,x的取值范围是___________.
12.若方程的正实数根为,设,其中m、n是两个连续的整数,则m+n=_________.
13.反比例函数(k>0)的图象经过点(1,y1)、(3,y2),则y1 y2.
14.反比例函数,在第一象限的图象如图所示,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,则△AOB的面积为__________.
15.如图,点A在反比例函数图像上,过点A作AB⊥x轴,垂足为点B,OA的垂直平分线交OB、OA于点C、D,当AB=时,△ABC的周长为 .
三、解答题
16.据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分).根据图像所示信息,解答下列问题:
(1)分别求出药物燃烧及释放过程中,y与x之间的函数解析式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始后,哪一时间段内师生不能进入教室?
17.如图,已知,是一次函数的图象
和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)观察图像:当反比例函数值大于一次函数值时,x的
取值范围为_____________;
(3)求的面积.
18.已知y=y1+y2,其中y1与x成正比例,y2与x﹣2成反比例.当x=1时,y=2;x=3时,y=10.求:
(1)y与x的函数关系式; (2)当x=﹣1时,y的值.
19.已知,如图,反比例函数的图像与一次函数y=x+3的图像交于点A(1,m),点B(﹣4,﹣1),
(1)请根据图像,直接写出不等式的解集;
(2)求△OAB的面积.
20.如图已知直线与x、y轴分别交于点A、B,与双曲线交于点C,过点C作CD⊥x轴于点D,连接OC,设C点坐标为(a,b),t=OD·DA.
(1)当a=4时,求的值;
(2)求证:
(3)随着a的变化,的值是否变化,若不变化,求出其值;若变化,请说明理由.
21.如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,C在y轴上,反比例函数y=(k≠0)的图象分别交BC,AB于E,F,已知OA=3,OC=4.
(1)若BF-BE=,求k的值;
(2)连接OE、OF,当四边形OEBF的面积为8时,求线段BE与CE的数量关系,并说明理由.
(3)在(1)的条件下,设点P是坐标轴上一动点,点Q是坐标平面内一点,若以E、F、P、Q四点为顶点的四边形是菱形,请直接写出P点的坐标.
22.如图,直线与反比例函数y= (x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的关系式;
(2)求点C的坐标.
(3)点M是x轴上的一个动点,
①若点M在线段OC上,且△AMB的面积为3,求点M的坐标。
②点N是平面直角坐标系中的一点,当以A、B、M、N四点为顶点的四边形是菱形时,请直接写出点N的坐标.
23.已知:如图1,在平面直角坐标系中点A(2,0),B(0,1),以AB为顶点在第一象限内作正方形ABCD.反比例函数、分别经过C、D两点.
⑴求点C的坐标并直接写出的值;
⑵如图2,过C、D两点分别作x、y轴的平行线得矩形CEDF,现将点D沿的图像向右运动,矩形CEDF随之平移.
①试求当点E落在的图像上时点D的坐标;
②设平移后点D的横坐标为a,当a>5时,试判断平移后的边CE与的图像有无公共点并说明理由.
图1 图2 备用图
参考答案
一、选择题
1.C
2.C
3.C
4.B
二、填空题
5.
6.
7.
8.
9.或
10.8
11.或
12.7
13.>
14.1
15.
三、解答题
16.解:(1)设反比例函数解析式为,
将(25,6)代入解析式得,k=25×6=150,
则函数解析式为(x>15),
将y=10代入解析式得,,x=15,故A(15,10),
设正比例函数解析式为,
将A(15,10)代入得:,解得:
则正比例函数解析式为(0<x≤15).
(2)3―75分钟内不能进入教室
17.(1) (2) (3)的面积为6
18.解:(1)∵,其中与成正比例,与成反比例,
∴设,,
∴y与x的函数关系式为.
将点(1,2)、(3,10)代入中,
得:,解得:,
∴y与x的函数关系式为.
(2)令,则.
19.解:(1)∵反比例函数的图象过点A(1,m),
∴,
∴A(1,4),
由图象可得不等式的解集为:或;
(2)∵一次函数中,当时,,
∴C(-3,0),
∴△OAB的面积为:.
20.解:(1)当时,代入得:
所以C(4,1)
将C(4,1)代入得:,解得:
所以一次函数解析式为:
令,则,所以A(5,0)
OA=5,DA=OA-OD=5-4=1
所以
所以
(2)将C(a,b)代入得:
所以C(a,ka+5)
将C(a,ka+5)代入得:
即:
(3),令,则,解得:
所以A(,0)
所以OA=,则DA=OA-OD=
则
21.解:(1)设,则,
则E(,),F(3,)
∵E、F都在反比例函数图象上
∴
解得:
∴F(3,2)
将F(3,2)代入得:
(2)∵四边形OEBF的面积为8
∴
∴
即:
由图可知E点纵坐标为4,代入得:
所以E(1,4)
所以,
∴
(3)(0,2)、(0,)、(,0)、(,0)
22.解:(1)∵点A的坐标为(-2,4),
∴,
∴反比例函数的关系式为:;
(2)当时,,
∴B(-4,2),
把点A(-2,4)和B(-4,2)代入得:
,
解得:,
∴,
令,则,解得:,
∴C(-6,0);
(3)①设,则
∵,
∴
∴
解得:
∴M(-3,0)
②(0,2)或(-6,6)
23.解:(1)过点C作CE⊥y轴,垂足为C
∵四边形ABCD为正方形,CE⊥y轴
∴∠AOB=∠BEC=∠ABC=90°,AB=BC
∴∠ABO+∠OAB=90°,∠ABO+∠CBE=90°
∴∠CBE=∠OAB
∴△ABO≌△BCE
∴BE=OA=2,CE=OB=1
∴OE=OB+BE=1+2=3
∴C(1,3)
将C(1,3)代入得:
同理可以求出:D(3,2)
将D(3,2)代入得:
(2)①设D(a,)
由(1)得:DE=2,则E(a-2,)
∵点E在图象上
∴
解得:
∴D(4,)
②平移后的边CE与的图像一定有公共点
由①得:E(a-2,)
由(1)得:CE=1
∴C(a-2,)
设直线CE与的图象交于F点
则F(a-2,)
∴
∵
∴
∴
∴
∴
∴
∴
∴F点在C点的下方
同理可证
∴F点在E点的上方
∴F点一定在CE边上
所以平移后的边CE与的图像一定有公共点
一、选择题
1.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
2.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
3.已知点A(m﹣2,y1)、B(m+1,y2)在反比例函数的图象上且y1>y2,则m范围是( )
A.m<-1 B.m>2 C.-1<m<2 D. 无法确定
4.在同一平面直角坐标系中,函数与的图象可能是( )
A. B. C. D.
二、填空题
5.在函数的图象上有三个点(-2,),(-1,),(,),则,,的大小关系为 .
6.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
7.设函数的图像的交点坐标是,则的值为 .
8.点A(x1,y1),点B(x2,y2)是反比例函数y=的图象上两点,若x1<0<x2,y1>y2,则k的取值范围是__________.
第6题图 第9题图 第10题图
9.如图,一次函数y =ax+b的图像与反比例函数的图像交于A(4,m)、B(﹣2,n)两点,则不等式的解集为______________.
10.如图,点A、B是双曲线上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为________.
第11题图 第14题图 第15题图
11.如图,反比例函数y=的图象经过点A(4,1),当y<1时,x的取值范围是___________.
12.若方程的正实数根为,设,其中m、n是两个连续的整数,则m+n=_________.
13.反比例函数(k>0)的图象经过点(1,y1)、(3,y2),则y1 y2.
14.反比例函数,在第一象限的图象如图所示,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,则△AOB的面积为__________.
15.如图,点A在反比例函数图像上,过点A作AB⊥x轴,垂足为点B,OA的垂直平分线交OB、OA于点C、D,当AB=时,△ABC的周长为 .
三、解答题
16.据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分).根据图像所示信息,解答下列问题:
(1)分别求出药物燃烧及释放过程中,y与x之间的函数解析式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始后,哪一时间段内师生不能进入教室?
17.如图,已知,是一次函数的图象
和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)观察图像:当反比例函数值大于一次函数值时,x的
取值范围为_____________;
(3)求的面积.
18.已知y=y1+y2,其中y1与x成正比例,y2与x﹣2成反比例.当x=1时,y=2;x=3时,y=10.求:
(1)y与x的函数关系式; (2)当x=﹣1时,y的值.
19.已知,如图,反比例函数的图像与一次函数y=x+3的图像交于点A(1,m),点B(﹣4,﹣1),
(1)请根据图像,直接写出不等式的解集;
(2)求△OAB的面积.
20.如图已知直线与x、y轴分别交于点A、B,与双曲线交于点C,过点C作CD⊥x轴于点D,连接OC,设C点坐标为(a,b),t=OD·DA.
(1)当a=4时,求的值;
(2)求证:
(3)随着a的变化,的值是否变化,若不变化,求出其值;若变化,请说明理由.
21.如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,C在y轴上,反比例函数y=(k≠0)的图象分别交BC,AB于E,F,已知OA=3,OC=4.
(1)若BF-BE=,求k的值;
(2)连接OE、OF,当四边形OEBF的面积为8时,求线段BE与CE的数量关系,并说明理由.
(3)在(1)的条件下,设点P是坐标轴上一动点,点Q是坐标平面内一点,若以E、F、P、Q四点为顶点的四边形是菱形,请直接写出P点的坐标.
22.如图,直线与反比例函数y= (x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的关系式;
(2)求点C的坐标.
(3)点M是x轴上的一个动点,
①若点M在线段OC上,且△AMB的面积为3,求点M的坐标。
②点N是平面直角坐标系中的一点,当以A、B、M、N四点为顶点的四边形是菱形时,请直接写出点N的坐标.
23.已知:如图1,在平面直角坐标系中点A(2,0),B(0,1),以AB为顶点在第一象限内作正方形ABCD.反比例函数、分别经过C、D两点.
⑴求点C的坐标并直接写出的值;
⑵如图2,过C、D两点分别作x、y轴的平行线得矩形CEDF,现将点D沿的图像向右运动,矩形CEDF随之平移.
①试求当点E落在的图像上时点D的坐标;
②设平移后点D的横坐标为a,当a>5时,试判断平移后的边CE与的图像有无公共点并说明理由.
图1 图2 备用图
参考答案
一、选择题
1.C
2.C
3.C
4.B
二、填空题
5.
6.
7.
8.
9.或
10.8
11.或
12.7
13.>
14.1
15.
三、解答题
16.解:(1)设反比例函数解析式为,
将(25,6)代入解析式得,k=25×6=150,
则函数解析式为(x>15),
将y=10代入解析式得,,x=15,故A(15,10),
设正比例函数解析式为,
将A(15,10)代入得:,解得:
则正比例函数解析式为(0<x≤15).
(2)3―75分钟内不能进入教室
17.(1) (2) (3)的面积为6
18.解:(1)∵,其中与成正比例,与成反比例,
∴设,,
∴y与x的函数关系式为.
将点(1,2)、(3,10)代入中,
得:,解得:,
∴y与x的函数关系式为.
(2)令,则.
19.解:(1)∵反比例函数的图象过点A(1,m),
∴,
∴A(1,4),
由图象可得不等式的解集为:或;
(2)∵一次函数中,当时,,
∴C(-3,0),
∴△OAB的面积为:.
20.解:(1)当时,代入得:
所以C(4,1)
将C(4,1)代入得:,解得:
所以一次函数解析式为:
令,则,所以A(5,0)
OA=5,DA=OA-OD=5-4=1
所以
所以
(2)将C(a,b)代入得:
所以C(a,ka+5)
将C(a,ka+5)代入得:
即:
(3),令,则,解得:
所以A(,0)
所以OA=,则DA=OA-OD=
则
21.解:(1)设,则,
则E(,),F(3,)
∵E、F都在反比例函数图象上
∴
解得:
∴F(3,2)
将F(3,2)代入得:
(2)∵四边形OEBF的面积为8
∴
∴
即:
由图可知E点纵坐标为4,代入得:
所以E(1,4)
所以,
∴
(3)(0,2)、(0,)、(,0)、(,0)
22.解:(1)∵点A的坐标为(-2,4),
∴,
∴反比例函数的关系式为:;
(2)当时,,
∴B(-4,2),
把点A(-2,4)和B(-4,2)代入得:
,
解得:,
∴,
令,则,解得:,
∴C(-6,0);
(3)①设,则
∵,
∴
∴
解得:
∴M(-3,0)
②(0,2)或(-6,6)
23.解:(1)过点C作CE⊥y轴,垂足为C
∵四边形ABCD为正方形,CE⊥y轴
∴∠AOB=∠BEC=∠ABC=90°,AB=BC
∴∠ABO+∠OAB=90°,∠ABO+∠CBE=90°
∴∠CBE=∠OAB
∴△ABO≌△BCE
∴BE=OA=2,CE=OB=1
∴OE=OB+BE=1+2=3
∴C(1,3)
将C(1,3)代入得:
同理可以求出:D(3,2)
将D(3,2)代入得:
(2)①设D(a,)
由(1)得:DE=2,则E(a-2,)
∵点E在图象上
∴
解得:
∴D(4,)
②平移后的边CE与的图像一定有公共点
由①得:E(a-2,)
由(1)得:CE=1
∴C(a-2,)
设直线CE与的图象交于F点
则F(a-2,)
∴
∵
∴
∴
∴
∴
∴
∴
∴F点在C点的下方
同理可证
∴F点在E点的上方
∴F点一定在CE边上
所以平移后的边CE与的图像一定有公共点
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
