人教版高中数学必修2课件:2.3.1 直线与平面垂直的判定(1)
文档属性
| 名称 | 人教版高中数学必修2课件:2.3.1 直线与平面垂直的判定(1) |  | |
| 格式 | zip | ||
| 文件大小 | 725.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-23 08:10:46 | ||
图片预览





文档简介
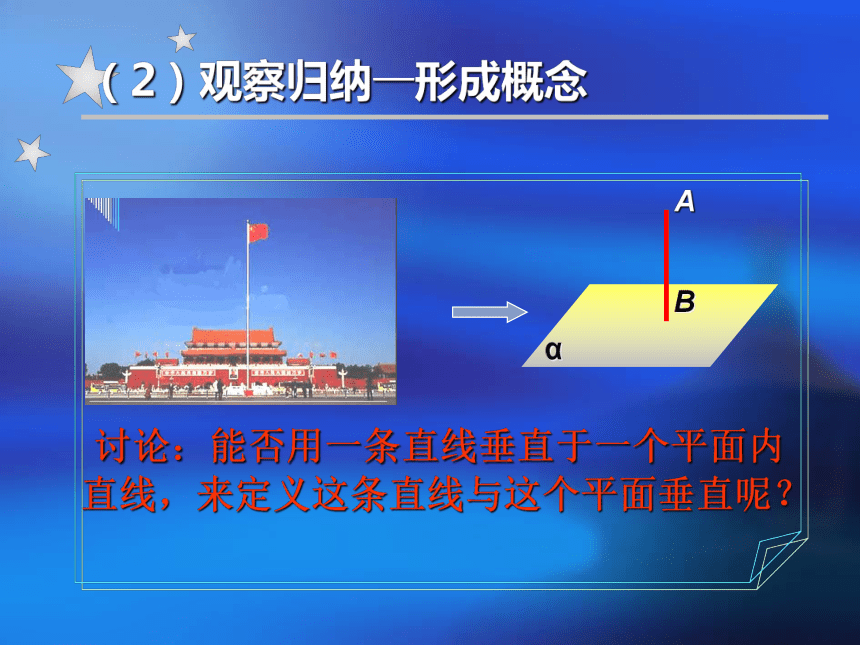
课件25张PPT。2.3.1直线与平面垂直的判定 (1)创设情境—感知概念 1.线面垂直定义(2)观察归纳—形成概念 讨论:能否用一条直线垂直于一个平面内
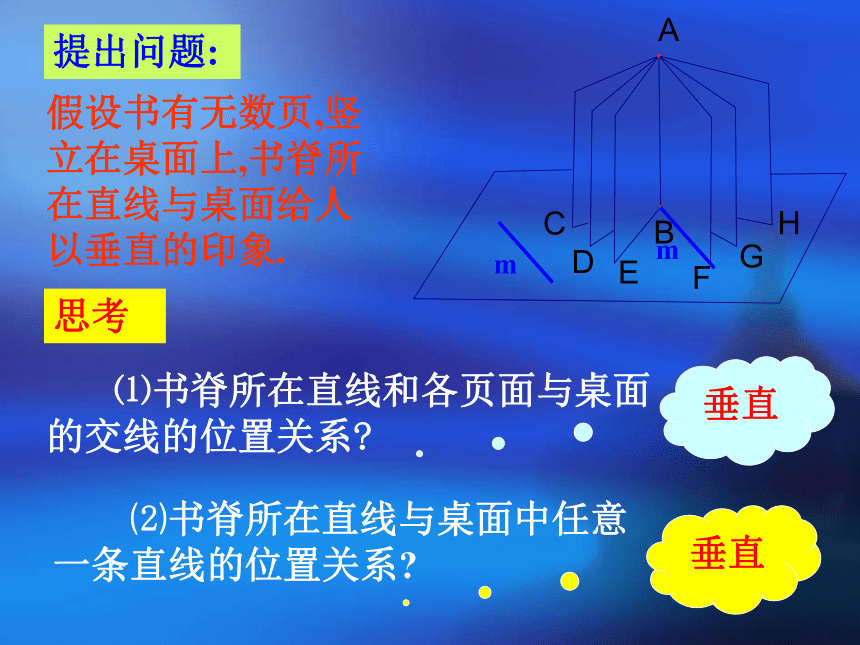
直线,来定义这条直线与这个平面垂直呢? 提出问题:假设书有无数页,竖立在桌面上,书脊所在直线与桌面给人以垂直的印象. 思考 ⑴书脊所在直线和各页面与桌面的交线的位置关系? ⑵书脊所在直线与桌面中任意一条直线的位置关系?直线与平面垂直的定义
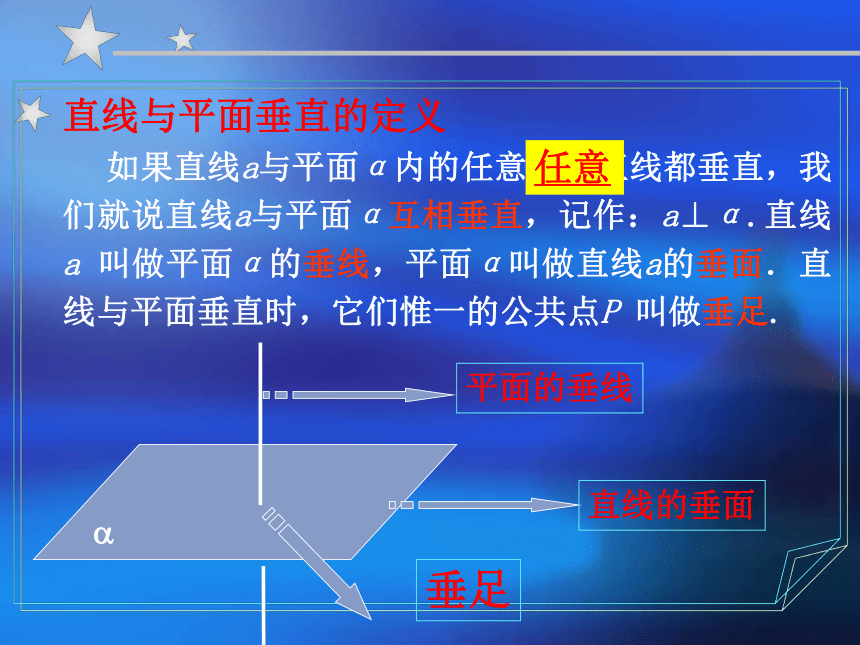
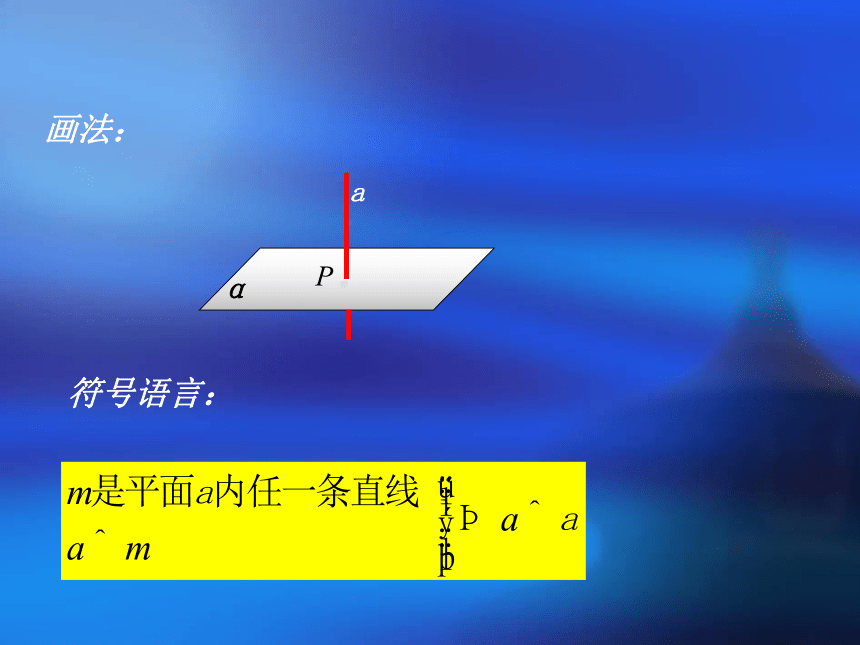
如果直线a与平面α内的任意一条直线都垂直,我们就说直线a与平面α互相垂直,记作:a⊥α.直线a 叫做平面α的垂线,平面α叫做直线a的垂面.直线与平面垂直时,它们惟一的公共点P 叫做垂足.任意平面的垂线直线的垂面垂足符号语言:画法:判断正误:
①如果一条直线垂直于一个平面内的无数条直线,那么,这条直线就与这个平面垂直。练习说 明⑴要证b?α,即证b垂直于α内的任一直线m. 问题1:如何将一张长方形贺卡直立于桌面?由此,你能猜想出判断一条直线与一个平面垂直的方法吗?2.线面垂直判定定理的探究猜想:一条直线与平面内两条相交直线都垂直,则该直线与此平面垂直。 实验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,将翻折后的纸片竖起放置在桌面上,(BD、DC 与桌面接触).问题
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD 与桌面所在的平 面垂直?(3)由折痕AD⊥BC ,翻折之后垂直关系,即AD⊥CD ,AD⊥BD 发生变化吗?由此你能得到什么结论?(4)有人说,折痕AD所在直线与桌面所在平面上的一条直线垂直,就可以判断AD垂直于平面,你同意他的说法吗?ABDCABCD@
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。 线不在多,重在相交线面垂直线线垂直直线与平面垂直的判定定理
→例1(P65例1).如图,已知a∥b,a⊥α,
求证:b ⊥α分析:要证b⊥α,只需在平面内找两条相交直线与之垂直。证明在平面 a 内作两条相交直线m ,n∵a⊥α∴a ⊥m, a ⊥n∴ b ⊥m, b⊥n∵mCa , nCa∴b ⊥αAC1DCA1D1BF例3 在正方体ABCD—A1B1C1D1 中,
求直线A1B与平面A1B1CD所成的角AC1DCBP变式:(1)求直线AC与平面A1B1CD所成的角(2)E,F分别是BC,CC1的中点,求EF与面ACC1A1所成的角.B1A1D1QB1EO练习
1. 两直线与一个平面所成的角相等,它们平行吗 ?
2.两平行直线和一个平面所成的角相等吗?解后反思: 通过本题的解答,你可以总结出什么解题思想和方法? 反思1:要证明直线与平面垂直可以运用判定定理;线线垂直 线面垂直反思2:能够运用定理的条件关键是要满足要与两条相交直线垂直说明:五个条件缺一不可 →反思3:由例1得到线面垂直的又一判定定理如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。动手探究3: 取一个边长为2的正方形,如图
(1)点E是AB的中点,点F是BC的中点,将△ABC, △DCF分别沿DE,DF折起,使A,C两点重合于点A’。则A’D与EF垂直吗?若能则说明理由。AEBCDFA’EOFD(2)你能在四面体A’-EFD中找出一个经过直线A’D且与EF垂直的平面?说出你的做法及理由。反思3: 运用定理的关键是找垂线,找垂线又经常会用到等腰三角形中三线合一,直角三角形,正方形,矩形中的直角等等。五.巩固练习 P67练习1如图:在三棱锥V-ABC中,VA=VC,AB=BC
求证:VABCD⊥VBAC解后反思要证线线垂直可以通过线面垂直来证明。
即线面垂直与线线垂直可以相互转化“平面化”是解决立体几何问题的一般思路。(2).如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。1.定义:如果一条直线垂于一个平面内的任何一条直线,则此直线垂直于这个平面.2.判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。线面垂直 →六.课堂小结.3.涉及的思想方法线线垂直→作业:
必做: P73 2 ,4
直线,来定义这条直线与这个平面垂直呢? 提出问题:假设书有无数页,竖立在桌面上,书脊所在直线与桌面给人以垂直的印象. 思考 ⑴书脊所在直线和各页面与桌面的交线的位置关系? ⑵书脊所在直线与桌面中任意一条直线的位置关系?直线与平面垂直的定义
如果直线a与平面α内的任意一条直线都垂直,我们就说直线a与平面α互相垂直,记作:a⊥α.直线a 叫做平面α的垂线,平面α叫做直线a的垂面.直线与平面垂直时,它们惟一的公共点P 叫做垂足.任意平面的垂线直线的垂面垂足符号语言:画法:判断正误:
①如果一条直线垂直于一个平面内的无数条直线,那么,这条直线就与这个平面垂直。练习说 明⑴要证b?α,即证b垂直于α内的任一直线m. 问题1:如何将一张长方形贺卡直立于桌面?由此,你能猜想出判断一条直线与一个平面垂直的方法吗?2.线面垂直判定定理的探究猜想:一条直线与平面内两条相交直线都垂直,则该直线与此平面垂直。 实验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,将翻折后的纸片竖起放置在桌面上,(BD、DC 与桌面接触).问题
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD 与桌面所在的平 面垂直?(3)由折痕AD⊥BC ,翻折之后垂直关系,即AD⊥CD ,AD⊥BD 发生变化吗?由此你能得到什么结论?(4)有人说,折痕AD所在直线与桌面所在平面上的一条直线垂直,就可以判断AD垂直于平面,你同意他的说法吗?ABDCABCD@
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。 线不在多,重在相交线面垂直线线垂直直线与平面垂直的判定定理
→例1(P65例1).如图,已知a∥b,a⊥α,
求证:b ⊥α分析:要证b⊥α,只需在平面内找两条相交直线与之垂直。证明在平面 a 内作两条相交直线m ,n∵a⊥α∴a ⊥m, a ⊥n∴ b ⊥m, b⊥n∵mCa , nCa∴b ⊥αAC1DCA1D1BF例3 在正方体ABCD—A1B1C1D1 中,
求直线A1B与平面A1B1CD所成的角AC1DCBP变式:(1)求直线AC与平面A1B1CD所成的角(2)E,F分别是BC,CC1的中点,求EF与面ACC1A1所成的角.B1A1D1QB1EO练习
1. 两直线与一个平面所成的角相等,它们平行吗 ?
2.两平行直线和一个平面所成的角相等吗?解后反思: 通过本题的解答,你可以总结出什么解题思想和方法? 反思1:要证明直线与平面垂直可以运用判定定理;线线垂直 线面垂直反思2:能够运用定理的条件关键是要满足要与两条相交直线垂直说明:五个条件缺一不可 →反思3:由例1得到线面垂直的又一判定定理如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。动手探究3: 取一个边长为2的正方形,如图
(1)点E是AB的中点,点F是BC的中点,将△ABC, △DCF分别沿DE,DF折起,使A,C两点重合于点A’。则A’D与EF垂直吗?若能则说明理由。AEBCDFA’EOFD(2)你能在四面体A’-EFD中找出一个经过直线A’D且与EF垂直的平面?说出你的做法及理由。反思3: 运用定理的关键是找垂线,找垂线又经常会用到等腰三角形中三线合一,直角三角形,正方形,矩形中的直角等等。五.巩固练习 P67练习1如图:在三棱锥V-ABC中,VA=VC,AB=BC
求证:VABCD⊥VBAC解后反思要证线线垂直可以通过线面垂直来证明。
即线面垂直与线线垂直可以相互转化“平面化”是解决立体几何问题的一般思路。(2).如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。1.定义:如果一条直线垂于一个平面内的任何一条直线,则此直线垂直于这个平面.2.判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。线面垂直 →六.课堂小结.3.涉及的思想方法线线垂直→作业:
必做: P73 2 ,4
