人教版必修四1.3 三角函数的诱导公式(1)课件(共26张PPT)
文档属性
| 名称 | 人教版必修四1.3 三角函数的诱导公式(1)课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-24 14:12:43 | ||
图片预览






文档简介
课件26张PPT。§1.3 三角函数的诱导公式(一) α的终边P(x,y)三角函数定义:同角三角函数的基本关系
平方关系:sin2α+cos2α=1
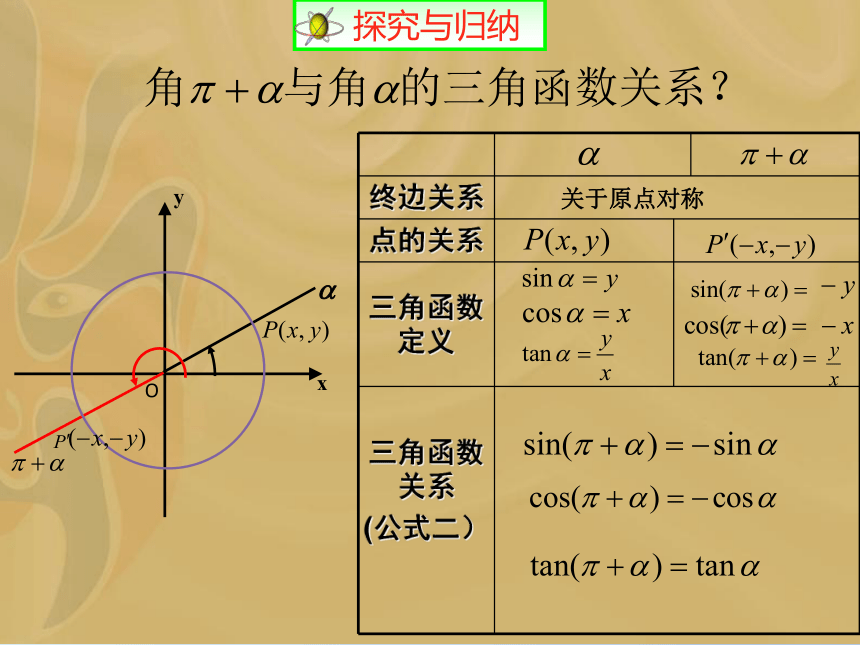
商数关系:tanα=sinα/cosα诱导公式一:终边相同角的同一三角函数的值相等探要点·究所然情境导学在前面的学习中,我们知道终边相同的角的同名三角函数相等,即公式一,并且利用公式一可以把绝对值较大的角的三角函数转化为0°~360°内的角的三角函数值,对于90°~360°内的三角函数我们能否进一步把它们转化到锐角范围内来求解?这就是本节学习的内容.Oxy关于原点对称-yxxyα-αp(x,y)p1(x,-y)关于x轴对称(x,-y)(x,y)关于y轴对称(-x,y)y-xxyαπ-α终边p(x,y)p1(-x,y)诱导公式二sin(π+α)=-sin α,
cos(π+α)=-cos α,
tan(π+α)=tan α.思考1 诱导公式二有何作用?
答 将第三象限角的三角函数转化为第一象限角的三角函数。
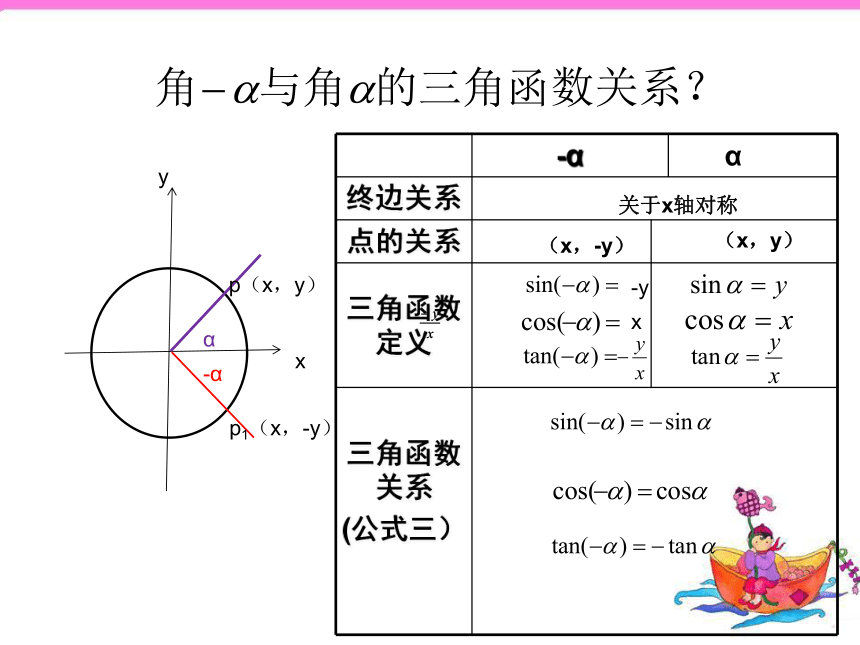
例如:诱导公式三sin(-α)=-sin α,
cos(-α)=cos α,
tan(-α)=-tan α.思考2 诱导公式三有何作用?
答 将负角的三角函数转化为正角的三角函数.
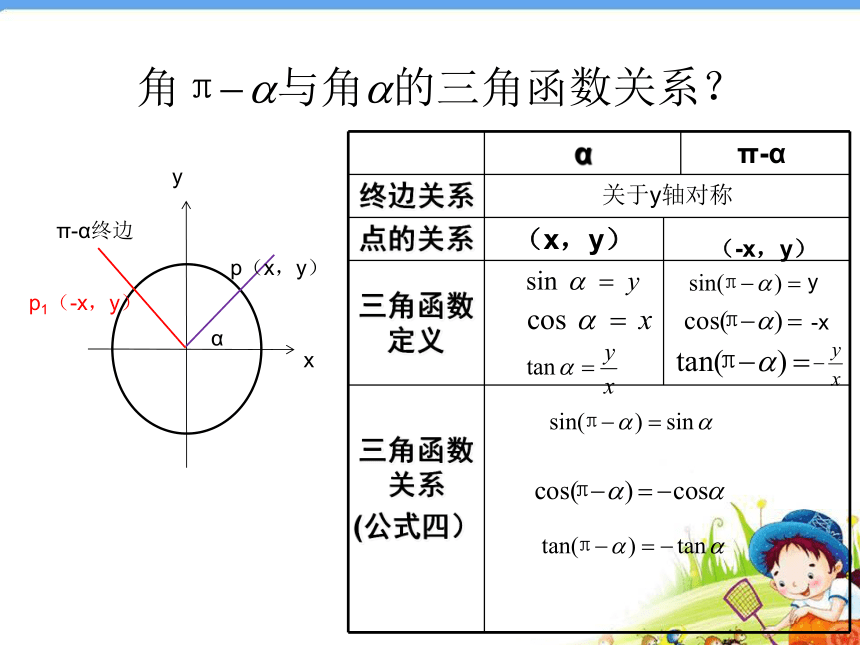
诱导公式四sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)=-tan α.思考3 诱导公式四有何作用?
答 将第二象限角的三角函数转化为第一象限角的三角函数.公式(三)
sin(-α)=
cos(-α)=
tan(-α)=-sinαcosα-tanα公式(四)
sin(π-α)=
cos(π-α)=
tan(π-α)=sinα-cosα-tanα公式(二)
sin(π+α)=
cos(π+α)=
tan(π+α)=
-sinα-cosαtanα函数名不变,符号看象限诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.例1 利用公式求下列三角函数的值:
(1)cos 225°;解 (1)cos 225°=cos(180°+45°)(4)cos(-2 040°).?反思与感悟 利用诱导公式求三角函数值时,先将不是[0,2π)内的角的三角函数,转化为[0,2π)内的角的三角函数,或先将负角转化为正角后再转化到 范围内的角的三角函数值.解 sin(-α-180°)=sin[-(180°+α)]
=-sin(180°+α)=-(-sin α)=sin α,
cos(-180°-α)=cos[-(180°+α)]
=cos(180°+α)=-cos α,反思与感悟 利用诱导公式进行化简,主要是进行角的转化,最终达到角的统一,能求值的要求出值.由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:(1)化负角的三角函数为正角的三角函数。(3)化为锐角的三角函数。 概括为:“负化正,正化小,化到锐角就终了。”用框图表示为:任意角的三角函数任意正角的三角函数用公式一或公式三公式一用公式二或公式四锐角三角函数1、计算2、化简1.诱导公式(1)结合图形
(2)函数名不变,符号看象限2.做题规律负角正角0~2π0~π锐角
平方关系:sin2α+cos2α=1
商数关系:tanα=sinα/cosα诱导公式一:终边相同角的同一三角函数的值相等探要点·究所然情境导学在前面的学习中,我们知道终边相同的角的同名三角函数相等,即公式一,并且利用公式一可以把绝对值较大的角的三角函数转化为0°~360°内的角的三角函数值,对于90°~360°内的三角函数我们能否进一步把它们转化到锐角范围内来求解?这就是本节学习的内容.Oxy关于原点对称-yxxyα-αp(x,y)p1(x,-y)关于x轴对称(x,-y)(x,y)关于y轴对称(-x,y)y-xxyαπ-α终边p(x,y)p1(-x,y)诱导公式二sin(π+α)=-sin α,
cos(π+α)=-cos α,
tan(π+α)=tan α.思考1 诱导公式二有何作用?
答 将第三象限角的三角函数转化为第一象限角的三角函数。
例如:诱导公式三sin(-α)=-sin α,
cos(-α)=cos α,
tan(-α)=-tan α.思考2 诱导公式三有何作用?
答 将负角的三角函数转化为正角的三角函数.
诱导公式四sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)=-tan α.思考3 诱导公式四有何作用?
答 将第二象限角的三角函数转化为第一象限角的三角函数.公式(三)
sin(-α)=
cos(-α)=
tan(-α)=-sinαcosα-tanα公式(四)
sin(π-α)=
cos(π-α)=
tan(π-α)=sinα-cosα-tanα公式(二)
sin(π+α)=
cos(π+α)=
tan(π+α)=
-sinα-cosαtanα函数名不变,符号看象限诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.例1 利用公式求下列三角函数的值:
(1)cos 225°;解 (1)cos 225°=cos(180°+45°)(4)cos(-2 040°).?反思与感悟 利用诱导公式求三角函数值时,先将不是[0,2π)内的角的三角函数,转化为[0,2π)内的角的三角函数,或先将负角转化为正角后再转化到 范围内的角的三角函数值.解 sin(-α-180°)=sin[-(180°+α)]
=-sin(180°+α)=-(-sin α)=sin α,
cos(-180°-α)=cos[-(180°+α)]
=cos(180°+α)=-cos α,反思与感悟 利用诱导公式进行化简,主要是进行角的转化,最终达到角的统一,能求值的要求出值.由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:(1)化负角的三角函数为正角的三角函数。(3)化为锐角的三角函数。 概括为:“负化正,正化小,化到锐角就终了。”用框图表示为:任意角的三角函数任意正角的三角函数用公式一或公式三公式一用公式二或公式四锐角三角函数1、计算2、化简1.诱导公式(1)结合图形
(2)函数名不变,符号看象限2.做题规律负角正角0~2π0~π锐角
