2018-2019学年山东省菏泽市牡丹区七年级(下)期中数学试卷(PDF解析版)
文档属性
| 名称 | 2018-2019学年山东省菏泽市牡丹区七年级(下)期中数学试卷(PDF解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 497.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-24 09:08:25 | ||
图片预览



文档简介
第 1 页(共 12 页)
2018-2019 学年山东省菏泽市牡丹区七年级(下)期中数学试卷
一、选择题
1.(3 分)下列各式中计算正确的是( )
A.2x+3y=5xy B.x
2
?x
3
=x
5
C.(a+b)
2
=a
2
+b
2
D.(3a
3
)
2
=9a
5
2.(3 分)下列多项式相乘,不能用平方差公式计算的是( )
A.(x﹣2y)(2y﹣x) B.(x﹣2y)(﹣x﹣2y)
C.(2y﹣x)(x+2y) D.(2y﹣x)(﹣x﹣2y)
3.(3 分)PM2.5 是大气压中直径小于或等于 0.0000025m 的颗粒物,将 0.0000025 用科学记数法表示为( )
A.0.25×10
﹣5
B.0.25×10
﹣6
C.2.5×10
﹣6
D.2.5×10
﹣5
4.(3 分)下列说法,其中错误的有( )
①相等的两个角是对顶角
②若∠1+∠2=180°,则∠1 与∠2 互为补角
③同位角相等
④垂线段最短
⑤同一平面内,两条直线的位置关系有:相交,平行和垂直
⑥过直线外一点,有且只有一条直线与这条直线平行
A.1 个 B.2 个 C.3 个 D.4 个
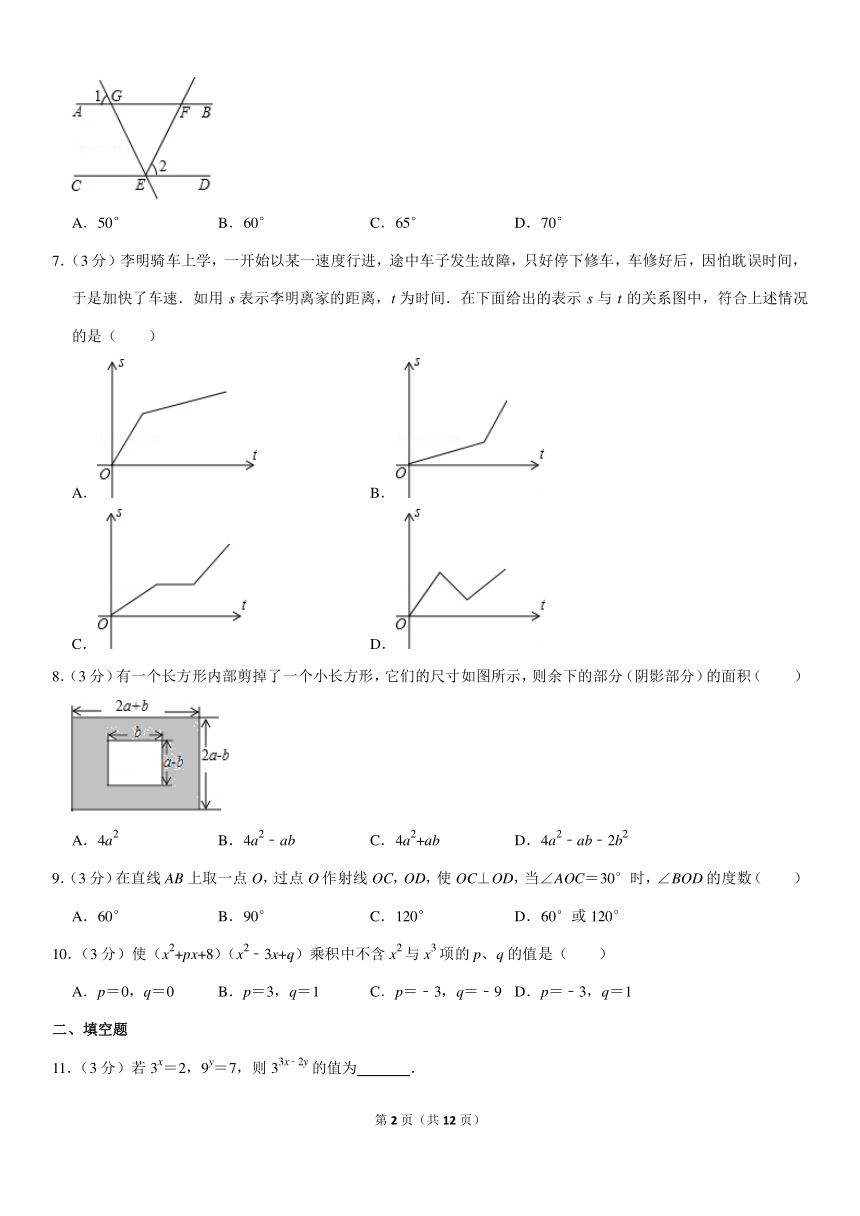
5.(3 分)如图,下列推理正确的是( )
A.因为∠BAD+∠ABC=180°,所以 AB∥CD
B.因为∠1=∠3,所以 AD∥BC
C.因为∠2=∠4,所以 AD∥BC
D.因为∠BAD+∠ADC=180°,所以 AD∥BC
6.(3 分)如图,AB∥CD,EF 平分∠GED,∠1=50°,则∠2=( )
第 2 页(共 12 页)
A.50° B.60° C.65° D.70°
7.(3 分)李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下修车,车修好后,因怕耽误时间,
于是加快了车速.如用 s 表示李明离家的距离,t 为时间.在下面给出的表示 s 与 t 的关系图中,符合上述情况
的是( )
A. B.
C. D.
8.(3 分)有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
A.4a
2
B.4a
2
﹣ab C.4a
2
+ab D.4a
2
﹣ab﹣2b
2
9.(3 分)在直线 AB 上取一点 O,过点 O 作射线 OC,OD,使 OC⊥OD,当∠AOC=30°时,∠BOD 的度数( )
A.60° B.90° C.120° D.60°或 120°
10.(3 分)使(x
2
+px+8)(x
2
﹣3x+q)乘积中不含 x
2
与 x
3
项的 p、q 的值是( )
A.p=0,q=0 B.p=3,q=1 C.p=﹣3,q=﹣9 D.p=﹣3,q=1
二、填空题
11.(3 分)若 3
x
=2,9
y
=7,则 3
3x﹣2y
的值为 .
第 3 页(共 12 页)
12.(3 分)已知 x
2
+(m﹣1)x+25 是完全平方式,则 m 的值为 .
13.(3 分)一个角的补角比它的余角的 2 倍大 40 度,则这个角的度数为 度.
14.(3 分)计算 = .
15.(3 分)如图,正方形卡片 A 类、B 类和长方形卡片 C 类若干张,如果用 A,、B、C 三类卡片拼成一个边长为(2a+3b)
的正方形,则需要 C 类卡片 张.
16.(3 分)如图,将一块含有 30°角的直角三角板的两个顶点放在矩形直尺的一组对边上,如果∠2=50°,那么
∠1 的度数为 .
17.(3 分)一蜡烛高 20 厘米,点燃后平均每小时燃掉 4 厘米,则蜡烛点燃后剩余的高度 h(厘米)与燃烧时间 t
(时)之间的关系式是 h= (0≤t≤5).
18.(3 分)我们学习的平方差公式不但可以使运算简便,也可以解决一些复杂的数学问题.尝试计算(2+1)(2
2
+1)
(2
3
+1)……(2
32
+1)的个位数字是 .
三、解答题
19.计算:
(1)
(2)2018×2020﹣2019
2
(3)(a+2b+3c)(a﹣3c﹣2b)
20.先化简,再求值:
(x+2y)(x﹣2y)﹣(8x
2
y
2
﹣20xy
3
)÷4xy,其中 x=2019,y=2020.
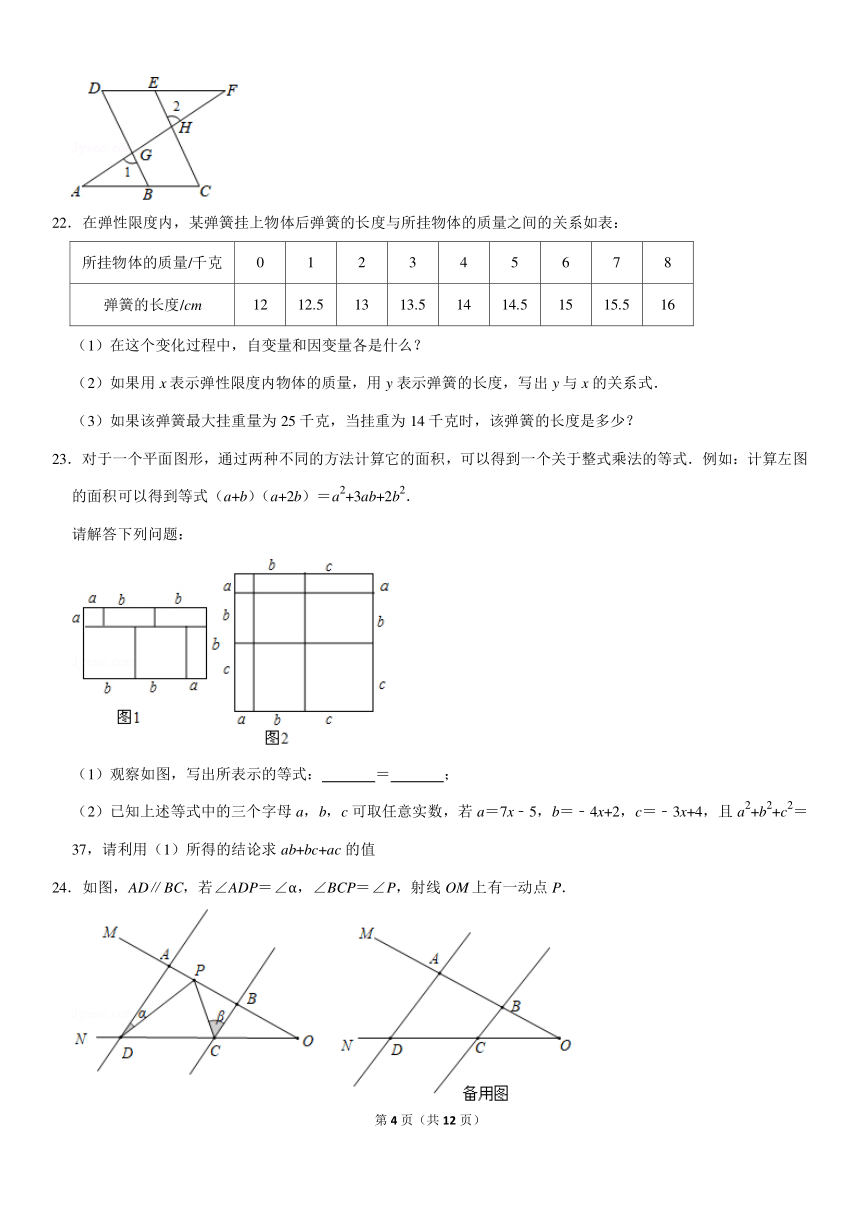
21.如图,已知∠1=∠2,∠C=∠D,证明 AC∥DF.
第 4 页(共 12 页)
22.在弹性限度内,某弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如表:
所挂物体的质量/千克 0 1 2 3 4 5 6 7 8
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5 16
(1)在这个变化过程中,自变量和因变量各是什么?
(2)如果用 x 表示弹性限度内物体的质量,用 y 表示弹簧的长度,写出 y 与 x 的关系式.
(3)如果该弹簧最大挂重量为 25 千克,当挂重为 14 千克时,该弹簧的长度是多少?
23.对于一个平面图形,通过两种不同的方法计算它的面积,可以得到一个关于整式乘法的等式.例如:计算左图
的面积可以得到等式(a+b)(a+2b)=a
2
+3ab+2b
2
.
请解答下列问题:
(1)观察如图,写出所表示的等式: = ;
(2)已知上述等式中的三个字母 a,b,c 可取任意实数,若 a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且 a
2
+b
2
+c
2
=
37,请利用(1)所得的结论求 ab+bc+ac 的值
24.如图,AD∥BC,若∠ADP=∠α,∠BCP=∠P,射线 OM 上有一动点 P.
第 5 页(共 12 页)
(1)当点 P 在 A,B 两点之间运动时,∠CPD 与∠α、∠β之间有何数量关系?请说明理由
(2)如果点 P 在 A、B 两点外侧运动时(点 P 与点 A、B、O 三点不重合),请你直接写出∠CPD 与∠α、∠β
之间的何数量关系.
第 6 页(共 12 页)
2018-2019 学年山东省菏泽市牡丹区七年级(下)期中数学试卷
参考答案与试题解析
一、选择题
1.【解答】解:A、2x+3y 无法计算,故此选项错误;
B、x
2
?x
3
=x
5
,正确;
C、(a+b)
2
=a
2
+2ab+b
2
,故此选项错误;
D、(3a
3
)
2
=9a
6
,故此选项错误;
故选:B.
2.【解答】解:A、(x﹣2y)(2y﹣x)=﹣(x﹣2y)(x﹣2y)=﹣(x﹣2y)
2
,不能用平方差公式计算;
B、(x﹣2y)(﹣x﹣2y)=(﹣2y+x)(﹣2y﹣x)=(﹣2y)
2
﹣x
2
=4y
2
﹣x
2
;
C、(2y﹣x)(x+2y)=(2y﹣x)(2y+x)=4y
2
﹣x
2
;
D、(2y﹣x)(﹣x﹣2y)=(﹣x+2y)(﹣x﹣2y)=(﹣x)
2
﹣(2y)
2
=x
2
﹣4y
2
.
故选:A.
3.【解答】解:0.0000025=2.5×10
﹣6
,
故选:C.
4.【解答】解:①相等的两个角不一定是对顶角,故错误;
②若∠1+∠2=180°,则∠1 与∠2 互为补角,故正确;
③同位角不一定相等,故错误;
④垂线段最短,故正确;
⑤在同一平面内,两条直线的位置关系有平行、相交,故错误;
⑥过直线外一点,有且只有一条直线与这条直线平行,故正确;
故选:C.
5.【解答】解:A、错误.由∠BAD+∠ABC=180°应该推出 AD∥BC.
B、正确.
C、错误.由∠2=∠4,应该推出 AB∥CD.
D、错误.由∠BAD+∠ADC=180°,应该推出 AB∥CD,
故选:B.
第 7 页(共 12 页)
6.【解答】解:∵∠1=50°,
∴∠BGE=50°.
∵AB∥CD,
∴∠GED=180°﹣∠BGE=130°.
∵EF 平分∠GED,
∴∠2= ∠GED=65°.
故选:C.
7.【解答】解;∵停下修车时,路程没变化,
观察图象,A、B、D 的路程始终都在变化,故错误;
C、修车是的路程没变化,故 C 正确;
故选:C.
8.【解答】解:余下的部分的面积为(2a+b)(2a﹣b)﹣b(a﹣b)
=4a
2
﹣b
2
﹣ab+b
2
=4a
2
﹣ab,
故选:B.
9.【解答】解:由 OC⊥OD,可得∠DOC=90°,
如图 1,当∠AOC=30°时,∠BOD=180°﹣30°﹣90°=60°;
如图 2,当∠AOC=30°时,∠AOD=90°﹣30°=60°,此时,∠BOD=180°﹣∠AOD=120°.
故选:D.
10.【解答】解:∵(x
2
+px+8)(x
2
﹣3x+q),
=x
4
﹣3x
3
+qx
2
+px
3
﹣3px
2
+pqx+8x
2
﹣24x+8q,
=x
4
+(p﹣3)x
3
+(q﹣3p+8)x
2
+(pq﹣24)x+8q.
∵乘积中不含 x
2
与 x
3
项,
第 8 页(共 12 页)
∴p﹣3=0,q﹣3p+8=0,
∴p=3,q=1.
故选:B.
二、填空题
11.【解答】解:3
3x﹣2y
=(3
x
)
3
÷9
y
=8÷7
= .
故答案为: .
12.【解答】解:∵(x±5)
2
=x
2
±10x+25,
∴m﹣1=±10,
∴m=11 或﹣9
故答案为:11 或﹣9.
13.【解答】解:设这个角为的度数为 x;根据题意得:
180°﹣x=2(90°﹣x)+40°,
解得 x=40°,
因此这个角的度数为 40°;
故答案为:40.
14.【解答】解:原式=(﹣ × )
2019
×
=﹣ .
故答案为:﹣ .
15.【解答】解:边长为(2a+3b)的正方形的面积为(2a+3b)(2a+3b)=4a
2
+12ab+9b
2
,
A 图形面积为 a
2
,B 图形面积为 b
2
,C 图形面积为 ab,
则可知需要 C 类卡片 12 张.
故答案为:12.
16.【解答】解:如图,∵m∥n,
第 9 页(共 12 页)
∴∠3=∠2=50°,
∵∠3=∠1+30°,
∴∠1=50°﹣30°=20°.
17.【解答】解:∵蜡烛点燃后平均每小时燃掉 4 厘米,
∴t 小时燃掉 4t 厘米,
由题意知:h=20﹣4t.
18.【解答】解:(2+1)(2
2
+1)(2
3
+1)……(2
32
+1)
=(2﹣1)(2+1)(2
2
+1)(2
3
+1)……(2
32
+1)
=(2
2
﹣1)(2
2
+1)(2
3
+1)……(2
32
+1)
=(2
4
﹣1)(2
3
+1)……(2
32
+1)
=(2
3
+1)(2
5
+1)……(2
31
+1)(2
64
﹣1)
∵2
1
=2,2
4
=4,2
3
=8,2
4
=16,.末尾是 2,4,8,6 四个一组循环,
∴2
64
﹣1 的个位是 5,
∵2
3
+1 个位是 9,2
5
+1 个位是 3,两个一组循环,
∴(2
3
+1)(2
5
+1)……(2
31
+1)的个位是 3,
∴(2
3
+1)(2
5
+1)……(2
31
+1)(2
64
﹣1)的个位是 5;
故答案是 5;
三、解答题
19.【解答】解:(1) =1+9﹣8=2;
(2)2018×2020﹣2019
2
=(2019﹣1)×(2019+1)﹣2019
2
=2019
2
﹣1﹣2019
2
=﹣1;
(3)(a+2b+3c)(a﹣3c﹣2b)=[a+(2b+3c)][a﹣(2b+3c)]=a
2
﹣(2b+3c)
2
=a
2
﹣4b
2
﹣9c
2
﹣12bc;
20.【解答】解:原式=x
2
﹣4y
2
﹣2xy+5y
2
=x
2
﹣2xy+y
2
,
第 10 页(共 12 页)
=(x﹣y)
2
,
当 x=2019,y=2020 时,
原式=(2019﹣2020)
2
=(﹣1)
2
=1.
21.【解答】证明:如图,
∵∠1=∠2(已知),∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABD(两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴DF∥AC(内错角相等,两直线平行).
22.【解答】解:(1)上表反映了:弹簧的长度(cm)与所挂物体的质量(kg)之间的关系,物体的质量是自变量,
弹簧的长度是因变量;
(2)如果用 x 表示弹性限度内物体的质量,用 y 表示弹簧的长度,那么 y 与 x 的关系式为:y=0.5x+12;
(3)当 x=14 时,y=0.5×14+12=19.
答:当挂重为 14 千克时,弹簧的长度 19cm.
23.【解答】解:(1)由图形可得等式:(a+b+c)
2
=a
2
+b
2
+c
2
+2ab+2bc+2ac;
故答案为:(a+b+c)
2
,a
2
+b
2
+c
2
+2ab+2bc+2ac;
(2)∵a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且 a
2
+b
2
+c
2
=37,
∴2ab+2bc+2ac=(a+b+c)
2
﹣(a
2
+b
2
+c
2
)
=(7x﹣5﹣4x+2﹣3x+4)
2
﹣37
=1
2
﹣37
=1﹣37
=﹣36.
第 11 页(共 12 页)
∴ab+bc+ac=﹣18.
24.【解答】解:(1)∠CPD=∠α+∠β,理由如下:
如图 1,过 P 作 PE∥AD 交 CD 于 E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)分两种情况:①当 P 在 BA 延长线时,∠CPD=∠β﹣∠α;
理由:如图 2,过 P 作 PE∥AD 交 CD 于 E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
②当 P 在 BO 之间时,∠CPD=∠α﹣∠β.
理由:如图 3,过 P 作 PE∥AD 交 CD 于 E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
第 12 页(共 12 页)
同课章节目录
