人教版数学八年级下册20. 1. 数据的集中趋势----平均数课件(22张)
文档属性
| 名称 | 人教版数学八年级下册20. 1. 数据的集中趋势----平均数课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-24 00:00:00 | ||
图片预览





文档简介
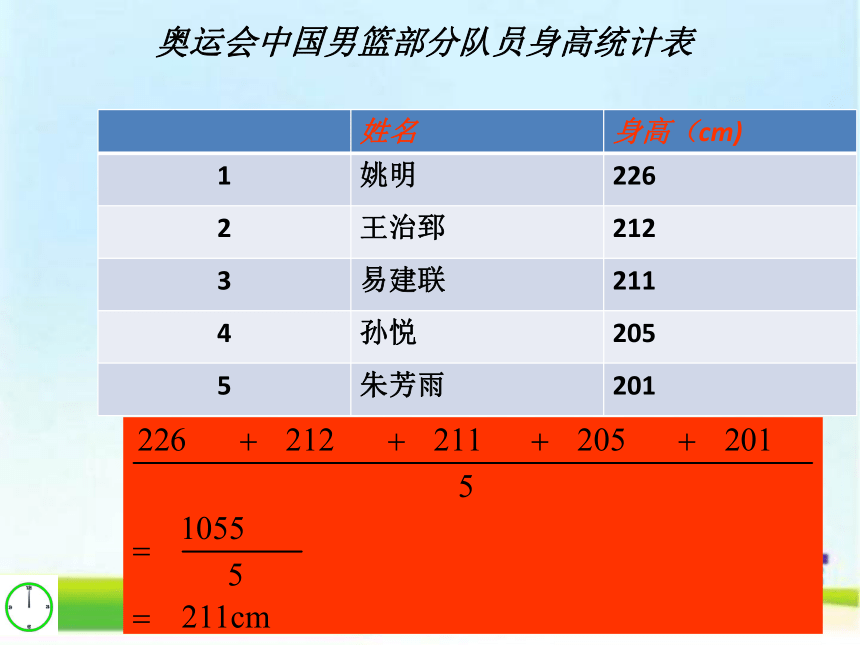
奥运会中国男篮部分队员身高统计表
姓名 身高(cm)
1 姚明 226
2 王治郅 212
3 易建联 211
4 孙悦 205
5 朱芳雨 201
(算术)平均数
问题:求一组数据的平均数有什么作用呢?
答:平均数可以用来描述一组数据的集中趋势。
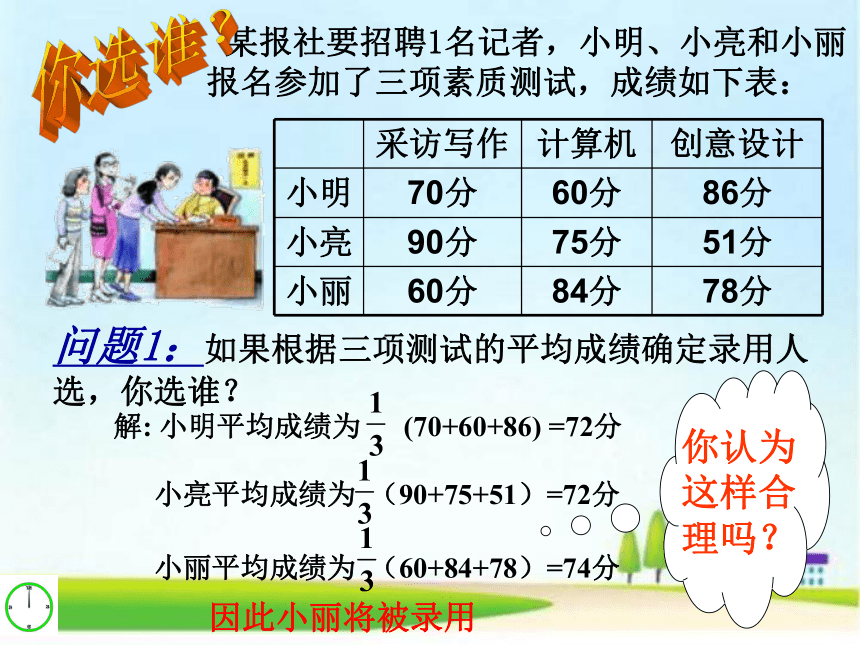
某报社要招聘1名记者,小明、小亮和小丽报名参加了三项素质测试,成绩如下表:
问题1:如果根据三项测试的平均成绩确定录用人选,你选谁?
因此小丽将被录用
你认为
这样合
理吗?
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
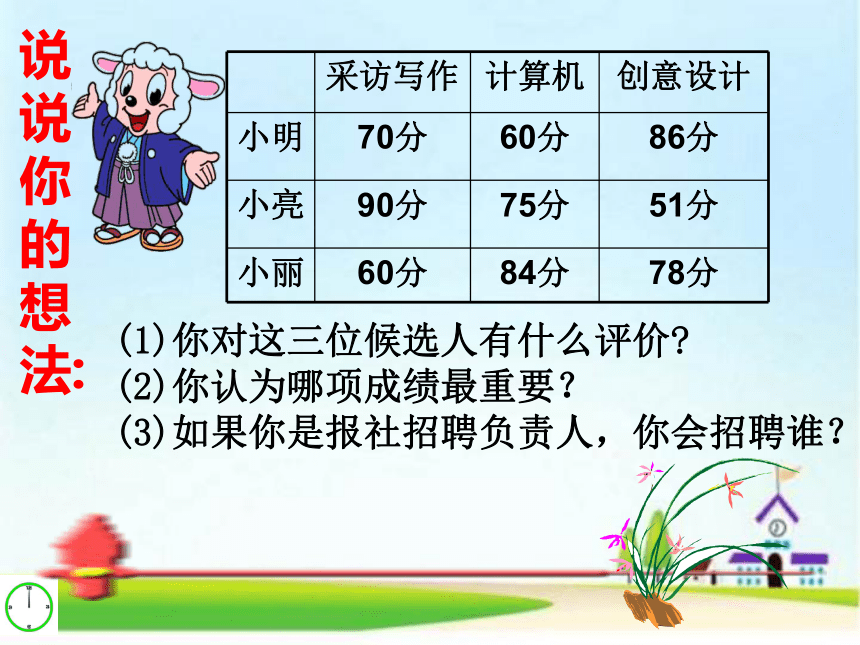
(1)你对这三位候选人有什么评价? (2)你认为哪项成绩最重要? (3)如果你是报社招聘负责人,你会招聘谁?
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
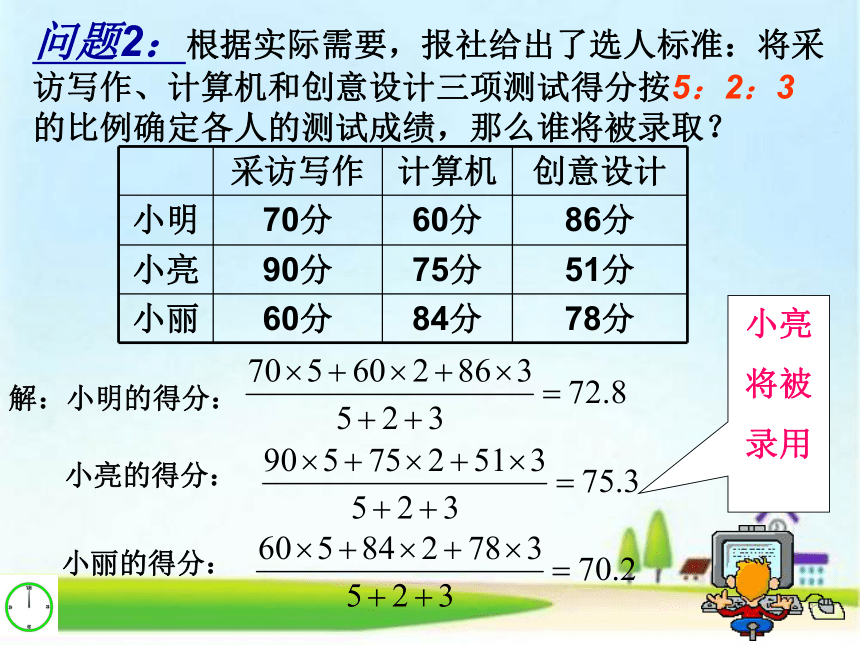
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
小亮
将被
录用
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
加权平均数
解法一:算术平均数 ( 略 )
解法二:成绩为6环的数据有1个,7环的数据有3个,8环的数据有5个,9环的数据有4个,10环的数据有2个,所以该运动员各次设计的平均成绩为
(环).
答:这次训练中该运动员射击的平均成绩为8.2环.
问题3、统计一名射击员运动员在某次训练中15次射击的中靶环数,获得如下数据:6, 7, 8, 7, 7, 8, 10, 9, 8, 8, 9, 9, 8, 10, 9.求这次训练中该运动员射击的平均成绩.
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
解:
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
问题3:
请思考:这三个问题中,分别用什么来表
示各个指标的重要程度的?
中靶环数 6 7 8 9 10
频数 1 3 5 4 2
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
问题3:
中靶环数 6 7 8 9 10
频数 1 3 5 4 2
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“权 ”。
“权”越大,对平均数的影响就越大。
归纳
权的常见形式:
3、百分数形式.如 30%、30% 、40%.
2、比的形式.如 5:2:3.
1、数据出现的次数.如 1、3、1、2.
某学校的卫生检查中,规定:教室卫生占30%、环境卫生占40%、个人卫生占30%。一天两个班级的各项卫生成绩分别如下:
那么哪个班的成绩高?
教室卫生 环境卫生 个人卫生
一班 85 90 95
二班 90 95 85
1)一组数据:44、x、35的平均数为53,则x的值为__练习:一组数据:x、y、5、6、8的平均数为7,则x、y的平均数为_,2x+5,2y-8,x+y的平均数为____.
做一做:
2)如果一组数据x1,x2, …xn的平均数是6,那么
(1)x1-3,x2-3, …xn-3的平均数是________
的平均数是_______.
2x1-1,2x2-1, …2xn-1的平均数是_______.
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
思考题:
一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24 所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
(2)求 4x+5, 4y+6, 4z+7 的平均数.
D
3、已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30
的平均数是b,则x1,x2,x3… x30的平均数是( )
4、若x1,x2… xn的平均数为a
(1)则数据x1+3,x2 +3 … xn +3的平均数为________.
(2)则数据10x1,10x2 … 10xn 的平均数为________.
a+3
10a
例2一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试。他们的各项成绩(百分制)如下:
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听、说、读、写成绩按照3:3:2:2的比确定,
则甲的成绩为
乙的成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
算
术
平
均
数
权
加
权
平
均
数
平
均
数
姓名 身高(cm)
1 姚明 226
2 王治郅 212
3 易建联 211
4 孙悦 205
5 朱芳雨 201
(算术)平均数
问题:求一组数据的平均数有什么作用呢?
答:平均数可以用来描述一组数据的集中趋势。
某报社要招聘1名记者,小明、小亮和小丽报名参加了三项素质测试,成绩如下表:
问题1:如果根据三项测试的平均成绩确定录用人选,你选谁?
因此小丽将被录用
你认为
这样合
理吗?
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
(1)你对这三位候选人有什么评价? (2)你认为哪项成绩最重要? (3)如果你是报社招聘负责人,你会招聘谁?
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
小亮
将被
录用
采访写作 计算机 创意设计
小明 70分 60分 86分
小亮 90分 75分 51分
小丽 60分 84分 78分
加权平均数
解法一:算术平均数 ( 略 )
解法二:成绩为6环的数据有1个,7环的数据有3个,8环的数据有5个,9环的数据有4个,10环的数据有2个,所以该运动员各次设计的平均成绩为
(环).
答:这次训练中该运动员射击的平均成绩为8.2环.
问题3、统计一名射击员运动员在某次训练中15次射击的中靶环数,获得如下数据:6, 7, 8, 7, 7, 8, 10, 9, 8, 8, 9, 9, 8, 10, 9.求这次训练中该运动员射击的平均成绩.
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
解:
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
问题3:
请思考:这三个问题中,分别用什么来表
示各个指标的重要程度的?
中靶环数 6 7 8 9 10
频数 1 3 5 4 2
问题2:根据实际需要,报社给出了选人标准:将采访写作、计算机和创意设计三项测试得分按5:2:3的比例确定各人的测试成绩,那么谁将被录取?
问题4: 很快,小亮的一个月的工作结束了,他的出勤、工作能力和工作实绩三项得分分别是100分、85分和88分,如果这3项成绩分别按30%、30%和40%的比例来计算,那么,小亮这个月的综合考评是多少分?
问题3:
中靶环数 6 7 8 9 10
频数 1 3 5 4 2
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“权 ”。
“权”越大,对平均数的影响就越大。
归纳
权的常见形式:
3、百分数形式.如 30%、30% 、40%.
2、比的形式.如 5:2:3.
1、数据出现的次数.如 1、3、1、2.
某学校的卫生检查中,规定:教室卫生占30%、环境卫生占40%、个人卫生占30%。一天两个班级的各项卫生成绩分别如下:
那么哪个班的成绩高?
教室卫生 环境卫生 个人卫生
一班 85 90 95
二班 90 95 85
1)一组数据:44、x、35的平均数为53,则x的值为__练习:一组数据:x、y、5、6、8的平均数为7,则x、y的平均数为_,2x+5,2y-8,x+y的平均数为____.
做一做:
2)如果一组数据x1,x2, …xn的平均数是6,那么
(1)x1-3,x2-3, …xn-3的平均数是________
的平均数是_______.
2x1-1,2x2-1, …2xn-1的平均数是_______.
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
思考题:
一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24 所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
(2)求 4x+5, 4y+6, 4z+7 的平均数.
D
3、已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30
的平均数是b,则x1,x2,x3… x30的平均数是( )
4、若x1,x2… xn的平均数为a
(1)则数据x1+3,x2 +3 … xn +3的平均数为________.
(2)则数据10x1,10x2 … 10xn 的平均数为________.
a+3
10a
例2一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试。他们的各项成绩(百分制)如下:
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听、说、读、写成绩按照3:3:2:2的比确定,
则甲的成绩为
乙的成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
算
术
平
均
数
权
加
权
平
均
数
平
均
数
