第九章 图形的相似单元综合测试题(含答案)
文档属性
| 名称 | 第九章 图形的相似单元综合测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 16:17:10 | ||
图片预览


文档简介
第九章 综合测试题
(时间:45分钟 分值:100分)
一、选择题(每题3分,共30分)
1.一条线段的黄金分割点有( )
A.1个 B.2个 C.3个 D.4个
2.已知=,那么下列等式中一定正确的是( )
A. B. C. D.
3.如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B.
C. D.
4.下列两个图形一定相似的是( )
A.两个菱形 B.两个矩形 C.两个正方形 D.两个平行四边形
5.如果△ABC与△DEF的相似比是1:5,则△ABC与△DEF的面积比为( )
A.1:25 B.1:5 C.1:2.5 D.1:5
6.如图所示,添加下列条件后仍不能判定△BAC∽△BDE的是( )
A.∠A=∠D B.∠ACB=∠DEB C. D.
7.如图所示,△ABO缩小后变为△A'B'O,其中A,B的对应点分别为A',B',A',B'均在图中格点上,若线段AB上有一点P(m,n),则点P在AB上的对应点P的坐标为( )
A.(,n) B.(m,n) C.(,) D.(m,)
8.如图所示,在正三角形ABC中,点D,E分别在AC,AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
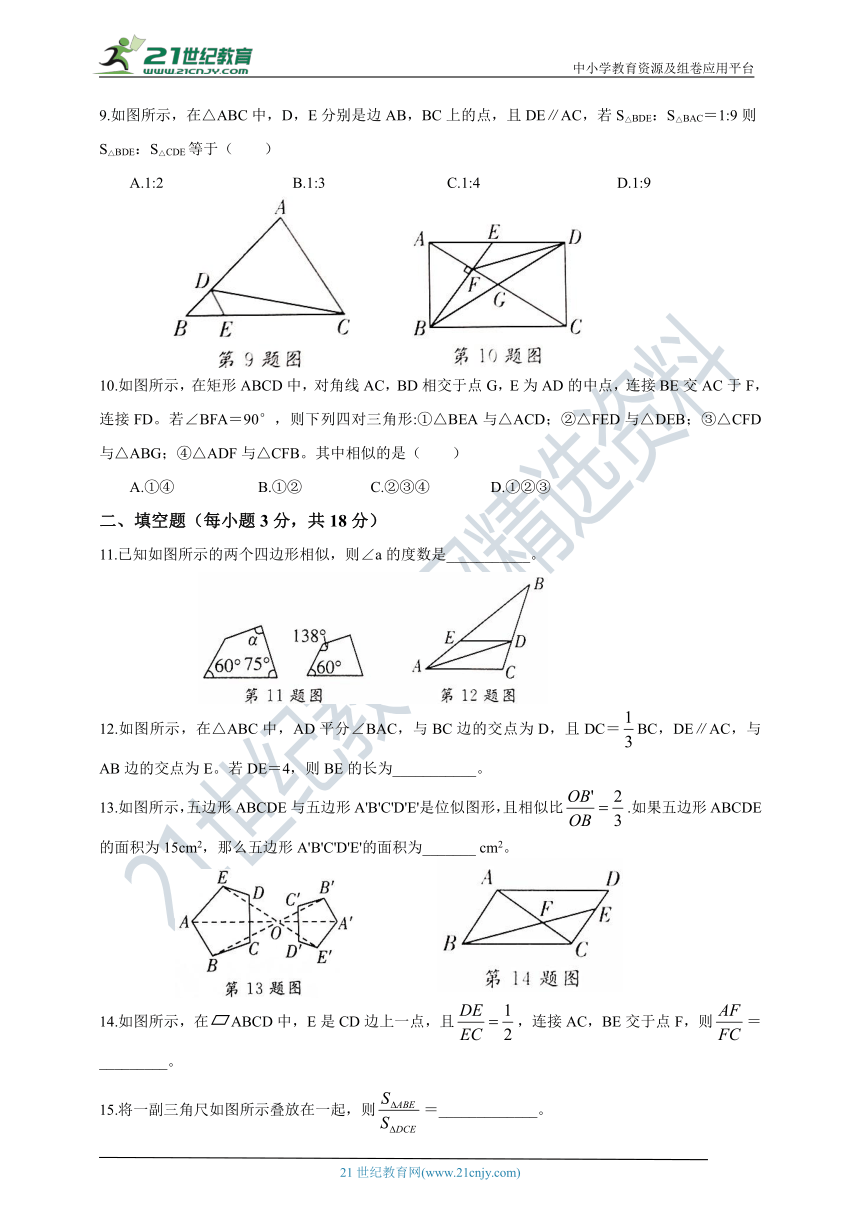
9.如图所示,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE:S△BAC=1:9则
S△BDE:S△CDE等于( )
A.1:2 B.1:3 C.1:4 D.1:9
10.如图所示,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD。若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB。其中相似的是( )
A.①④ B.①② C.②③④ D.①②③
二、填空题(每小题3分,共18分)
11.已知如图所示的两个四边形相似,则∠a的度数是___________。
12.如图所示,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=BC,DE∥AC,与AB边的交点为E。若DE=4,则BE的长为___________。
13.如图所示,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且相似比.如果五边形ABCDE的面积为15cm2,那么五边形A'B'C'D'E'的面积为_______ cm2。
14.如图所示,在 ABCD中,E是CD边上一点,且,连接AC,BE交于点F,则=_________。
15.将一副三角尺如图所示叠放在一起,则=_____________。
16.如图所示,小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,此时测得地面上的影长为8米,坡面上的影长为4米。已知斜坡与水平地面的夹角为30°,同一时刻,一根长为1米垂直于地面放置的标杆在地面上的影长为2米,则树的高度为___________米。
三、解答题(共52分)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上。
(1)点A的坐标为_________,点C的坐标为__________;
(2)画△A1B1C1,使它与△ABC关于原点O位似,且相似比为1:2,此时点A1的坐标为________。
18.(7分)如图所示,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长。
19.(8分)定义:如图①,点C在线段AB上,若满足AC2=BC·AB,则称点C为线段AB的黄金分割点。如图②,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D。
(1)求证:点D是线段AC的黄金分割点;
(2)求线段AD的长。
20.(8分)如图所示,在平行四边形ABCD中,对角线AC,BD交于点O,M为AD的中点,连接
CM交BD于点N,且ON=1。
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积。
21.(10分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆的高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛离地面的高度EF=1.6 m,人与标杆CD的水平距离FD=2 m,求旗杆AB的高度。
22.(13分)如图所示,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)。
(1)求直线AD的函数表达式;
(2)设直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标。
参考答案及解析
一、选择题
1.B 2.A 3.A 4.C 5.A 6.D 7.C 8.B 9.A 10.D
二、填空题
11.87° 12.8 13. 14. 15. 16.(6+)
三、解答题
17.(1)(0,4) (6,4)
(2)如图所示,△A1B1C1即为所求,点A1的坐标为(0,2)或(0,-2)。
18、解::∠ABC=90°,AD∥BC,∴∠A=180°-∠B=90°。∴∠PAD=∠PBC=90o。
设AP的长为x,则BP的长为8-x。
①若△APD∽△BPC,则AP:BP=AD: BC。
即x:(8-x)=3:4,解得x=;
②若△APD∽△BCP,同理①可得x=2或x=6。
∴AP的长为或2或6。
19、解:(1)证明:AB=AC=1,∠A=36°,∴∠ABC=∠C=(180o-∠A)=72o。
∵BD平分∠ABC,∴∠ABD=∠CBD=∠ABC=36o。∴∠BDC=72°。
∴DA=DB, BD=BC。∴AD=BD=BC。
∴∠CBD=∠A、∠C=∠C,∴△BDC∽△ABC,
∴,即BC2=DC?AC。∴AD2=DC?AC。
∷点D是线段AC的黄金分割点。
(2)AB=AC=1,DC=1-AD。
由(1)AD2=DC?AC、得AD2=(1-AD)?1,
解得AD=,(负值舍去)。∴AD=。
20.解:(1)?四边形ABCD是平行四边形,∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠CBN。∴△MND∽△CNB,
∴。∵M为AD的中点,∴MD=AD=BC,即。
∴,即BN=2DN.
设OB=x,则BN=x+1,DN=x-1,∴x+1=2(x-1),解得x=3。
∴BD=2×3=6。
(2)由(1)知MN:CN=DN:BN=1:2,S△MND=S△DCN=1,S△BNC=4S△MND=4.
∴S△ABD=S△BCD=6。∴S四边形ABNM=S△ABD-S△MAD=6-1=5。
21.解:如图所示,作EH⊥AB于点H,交CD于点G.
∵CD⊥FB,AB⊥FB。∴CD∥AB。易得△CGE∽△AHE,
∴,即,即,
解得AH=11.9,
∴AB=AH+HB=AH+EF=11. 9+1.6=13.5(m)。
∴旗杆AB的高度为13.5 m。
22.(1);
(2)点E坐标为(2,2)或(3,)。
(时间:45分钟 分值:100分)
一、选择题(每题3分,共30分)
1.一条线段的黄金分割点有( )
A.1个 B.2个 C.3个 D.4个
2.已知=,那么下列等式中一定正确的是( )
A. B. C. D.
3.如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B.
C. D.
4.下列两个图形一定相似的是( )
A.两个菱形 B.两个矩形 C.两个正方形 D.两个平行四边形
5.如果△ABC与△DEF的相似比是1:5,则△ABC与△DEF的面积比为( )
A.1:25 B.1:5 C.1:2.5 D.1:5
6.如图所示,添加下列条件后仍不能判定△BAC∽△BDE的是( )
A.∠A=∠D B.∠ACB=∠DEB C. D.
7.如图所示,△ABO缩小后变为△A'B'O,其中A,B的对应点分别为A',B',A',B'均在图中格点上,若线段AB上有一点P(m,n),则点P在AB上的对应点P的坐标为( )
A.(,n) B.(m,n) C.(,) D.(m,)
8.如图所示,在正三角形ABC中,点D,E分别在AC,AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
9.如图所示,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE:S△BAC=1:9则
S△BDE:S△CDE等于( )
A.1:2 B.1:3 C.1:4 D.1:9
10.如图所示,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD。若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB。其中相似的是( )
A.①④ B.①② C.②③④ D.①②③
二、填空题(每小题3分,共18分)
11.已知如图所示的两个四边形相似,则∠a的度数是___________。
12.如图所示,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC=BC,DE∥AC,与AB边的交点为E。若DE=4,则BE的长为___________。
13.如图所示,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且相似比.如果五边形ABCDE的面积为15cm2,那么五边形A'B'C'D'E'的面积为_______ cm2。
14.如图所示,在 ABCD中,E是CD边上一点,且,连接AC,BE交于点F,则=_________。
15.将一副三角尺如图所示叠放在一起,则=_____________。
16.如图所示,小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,此时测得地面上的影长为8米,坡面上的影长为4米。已知斜坡与水平地面的夹角为30°,同一时刻,一根长为1米垂直于地面放置的标杆在地面上的影长为2米,则树的高度为___________米。
三、解答题(共52分)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上。
(1)点A的坐标为_________,点C的坐标为__________;
(2)画△A1B1C1,使它与△ABC关于原点O位似,且相似比为1:2,此时点A1的坐标为________。
18.(7分)如图所示,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长。
19.(8分)定义:如图①,点C在线段AB上,若满足AC2=BC·AB,则称点C为线段AB的黄金分割点。如图②,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D。
(1)求证:点D是线段AC的黄金分割点;
(2)求线段AD的长。
20.(8分)如图所示,在平行四边形ABCD中,对角线AC,BD交于点O,M为AD的中点,连接
CM交BD于点N,且ON=1。
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积。
21.(10分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆的高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛离地面的高度EF=1.6 m,人与标杆CD的水平距离FD=2 m,求旗杆AB的高度。
22.(13分)如图所示,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)。
(1)求直线AD的函数表达式;
(2)设直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标。
参考答案及解析
一、选择题
1.B 2.A 3.A 4.C 5.A 6.D 7.C 8.B 9.A 10.D
二、填空题
11.87° 12.8 13. 14. 15. 16.(6+)
三、解答题
17.(1)(0,4) (6,4)
(2)如图所示,△A1B1C1即为所求,点A1的坐标为(0,2)或(0,-2)。
18、解::∠ABC=90°,AD∥BC,∴∠A=180°-∠B=90°。∴∠PAD=∠PBC=90o。
设AP的长为x,则BP的长为8-x。
①若△APD∽△BPC,则AP:BP=AD: BC。
即x:(8-x)=3:4,解得x=;
②若△APD∽△BCP,同理①可得x=2或x=6。
∴AP的长为或2或6。
19、解:(1)证明:AB=AC=1,∠A=36°,∴∠ABC=∠C=(180o-∠A)=72o。
∵BD平分∠ABC,∴∠ABD=∠CBD=∠ABC=36o。∴∠BDC=72°。
∴DA=DB, BD=BC。∴AD=BD=BC。
∴∠CBD=∠A、∠C=∠C,∴△BDC∽△ABC,
∴,即BC2=DC?AC。∴AD2=DC?AC。
∷点D是线段AC的黄金分割点。
(2)AB=AC=1,DC=1-AD。
由(1)AD2=DC?AC、得AD2=(1-AD)?1,
解得AD=,(负值舍去)。∴AD=。
20.解:(1)?四边形ABCD是平行四边形,∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠CBN。∴△MND∽△CNB,
∴。∵M为AD的中点,∴MD=AD=BC,即。
∴,即BN=2DN.
设OB=x,则BN=x+1,DN=x-1,∴x+1=2(x-1),解得x=3。
∴BD=2×3=6。
(2)由(1)知MN:CN=DN:BN=1:2,S△MND=S△DCN=1,S△BNC=4S△MND=4.
∴S△ABD=S△BCD=6。∴S四边形ABNM=S△ABD-S△MAD=6-1=5。
21.解:如图所示,作EH⊥AB于点H,交CD于点G.
∵CD⊥FB,AB⊥FB。∴CD∥AB。易得△CGE∽△AHE,
∴,即,即,
解得AH=11.9,
∴AB=AH+HB=AH+EF=11. 9+1.6=13.5(m)。
∴旗杆AB的高度为13.5 m。
22.(1);
(2)点E坐标为(2,2)或(3,)。
