六年级上册数学课件-8.1数学广角—数与形 运用数形结合发现规律(人教版) (2份打包)
文档属性
| 名称 | 六年级上册数学课件-8.1数学广角—数与形 运用数形结合发现规律(人教版) (2份打包) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 14:49:01 | ||
图片预览




文档简介
(共15张PPT)
人教版 数学 六年级 上册
运用数形结合发现规律
情境导入
探究新知
课堂小结
课后作业
数学广角—数与形
课堂练习
8
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
情境导入
连续的奇数相加
探究新知
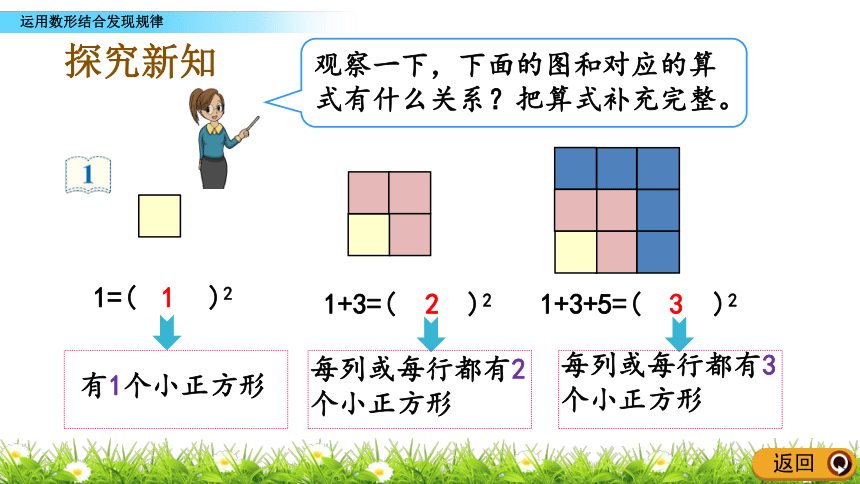
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
观察一下,下面的图和对应的算式有什么关系?把算式补充完整。
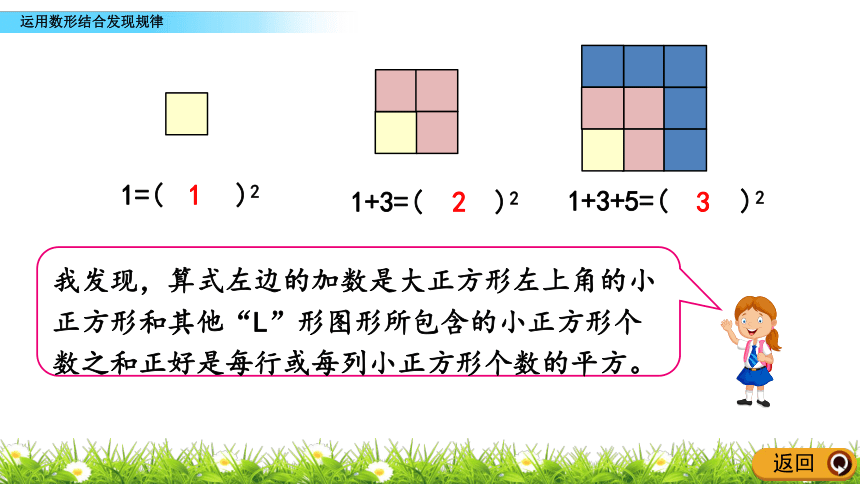
1=( )2
1+3=( )2
1
2
3
我发现,算式左边的加数是大正方形左上角的小正方形和其他“L”形图形所包含的小正方形个数之和正好是每行或每列小正方形个数的平方。
1+3+5=( )2
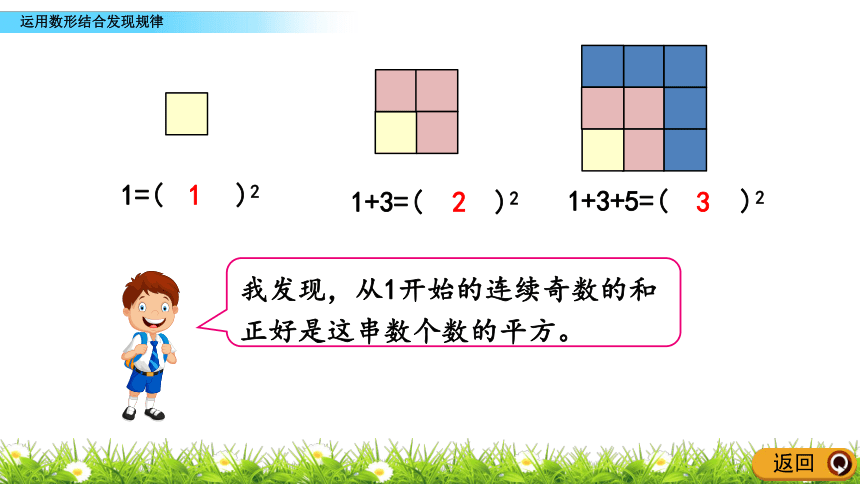
1=( )2
1+3=( )2
1
2
3
1+3+5=( )2
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从右上角加上其它L形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
课堂练习
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
红色正方形个数形成了1,2,3,4,…的数列,
蓝色正方形个数形成了8,10,12,14,…的数列。
中间每增加1个红色正方形,上下都必须增加2个蓝色正方形。
后一个图都比前一个图增加1个红色小正方形和2个蓝色小正方形。
3. 你能根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
72
62
72
62
4. 下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
课堂小结
课后作业
1.从教材课后练习选取;2.从课时练中选取。
人教版 数学 六年级 上册
运用数形结合发现规律
情境导入
探究新知
课堂小结
课后作业
数学广角—数与形
课堂练习
8
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
情境导入
连续的奇数相加
探究新知
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
观察一下,下面的图和对应的算式有什么关系?把算式补充完整。
1=( )2
1+3=( )2
1
2
3
我发现,算式左边的加数是大正方形左上角的小正方形和其他“L”形图形所包含的小正方形个数之和正好是每行或每列小正方形个数的平方。
1+3+5=( )2
1=( )2
1+3=( )2
1
2
3
1+3+5=( )2
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从右上角加上其它L形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
课堂练习
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
红色正方形个数形成了1,2,3,4,…的数列,
蓝色正方形个数形成了8,10,12,14,…的数列。
中间每增加1个红色正方形,上下都必须增加2个蓝色正方形。
后一个图都比前一个图增加1个红色小正方形和2个蓝色小正方形。
3. 你能根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
72
62
72
62
4. 下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
课堂小结
课后作业
1.从教材课后练习选取;2.从课时练中选取。
