11.1 .1三角形的边课件(33张PPT)
文档属性
| 名称 | 11.1 .1三角形的边课件(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 09:42:04 | ||
图片预览





文档简介
课件33张PPT。11.1 与三角形有关的线段
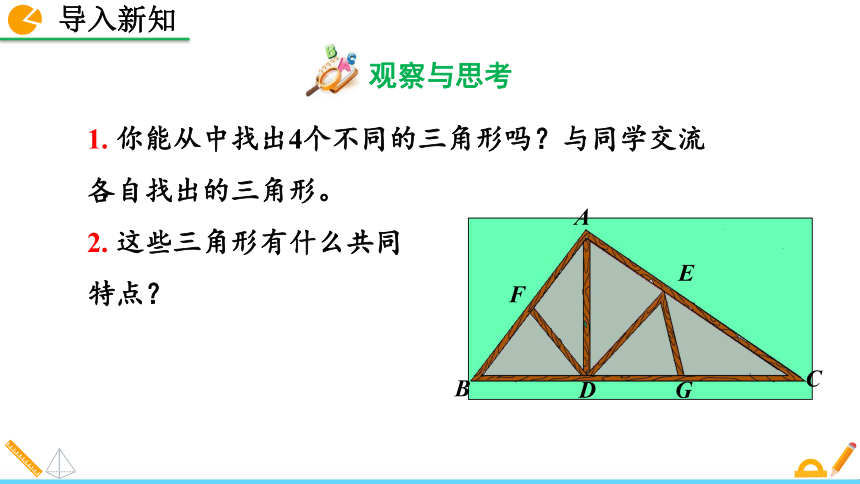
11.1.1 三角形的边人教版 数学 八年级 上册观察与思考1. 你能从中找出4个不同的三角形吗?与同学交流各自找出的三角形。 2. 这些三角形有什么共同
特点?EDEFGABC3. 培养学生的观察、分析、比较、操作能力,进一步发展空间观念,提高学生的探索能力.
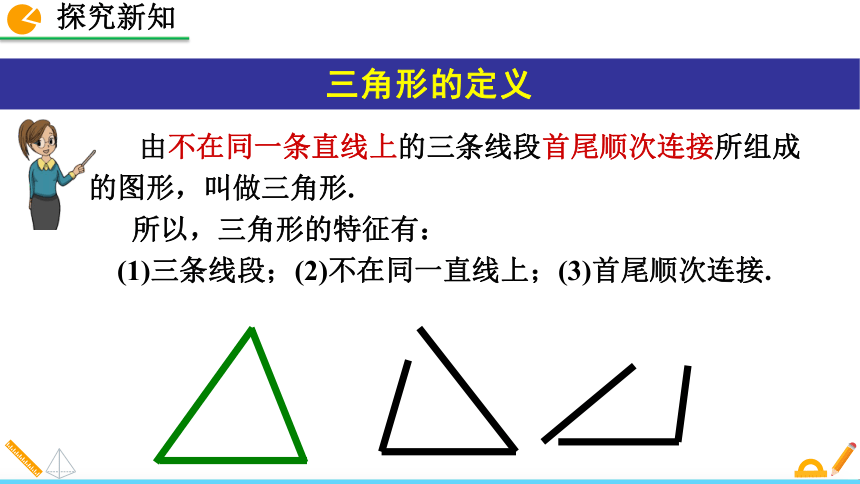
1. 掌握三角形的有关概念,会用符号表示三角形,会对三角形进行分类.2. 理解“三角形中任意两边的和大于第三边”的含义,并能运用它解决简单的实际问题.素养目标三角形的有关概念 三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗? 由不在同一条直线上的三条线段首尾顺次连接所组成的图形,叫做三角形.
所以,三角形的特征有:
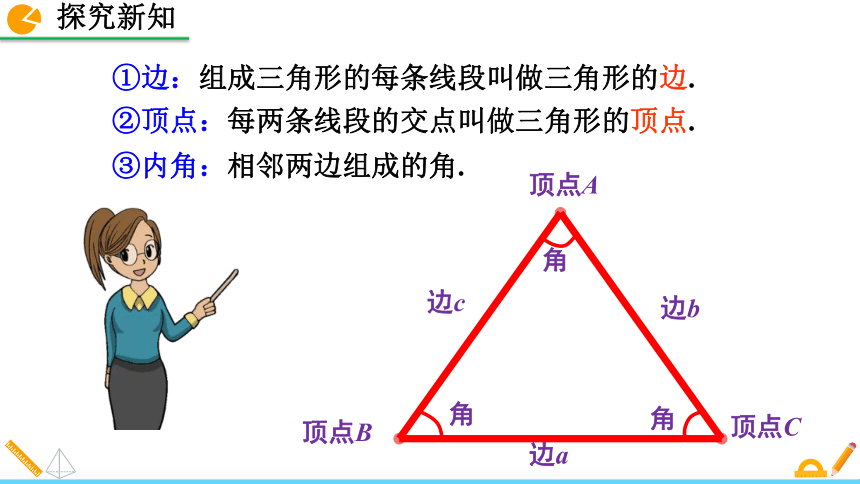
(1)三条线段;(2)不在同一直线上;(3)首尾顺次连接.三角形的定义 边c边b边a顶点A顶点B顶点C角角角①边:组成三角形的每条线段叫做三角形的边.
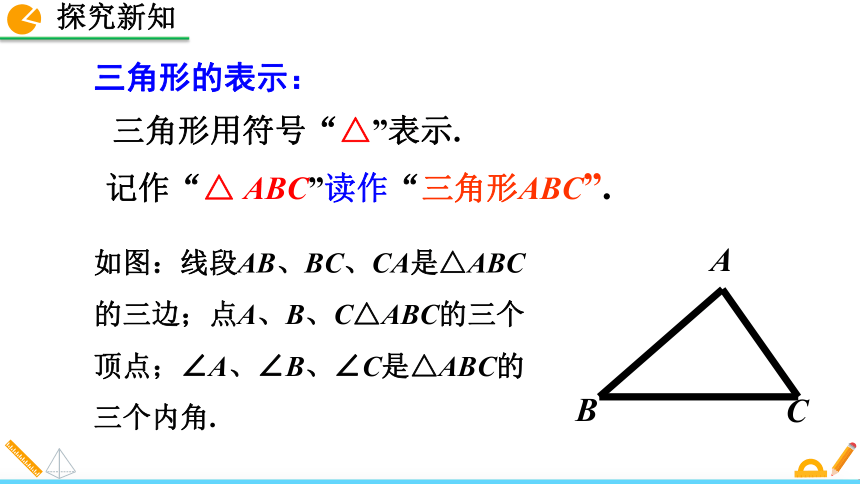
②顶点:每两条线段的交点叫做三角形的顶点.③内角:相邻两边组成的角.三角形的表示:三角形用符号“△”表示.记作“△ ABC”读作“三角形ABC”.如图:线段AB、BC、CA是△ABC的三边;点A、B、C△ABC的三个顶点;∠A、∠B、∠C是△ABC的三个内角.例1 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角.三角形的识别解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
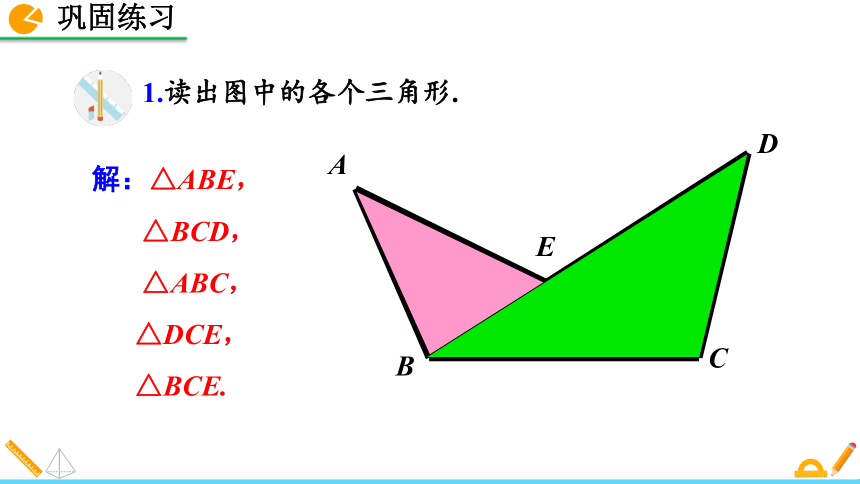
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E. 在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.1.读出图中的各个三角形.解:△ABE,
△BCD,
△ABC,
△DCE,
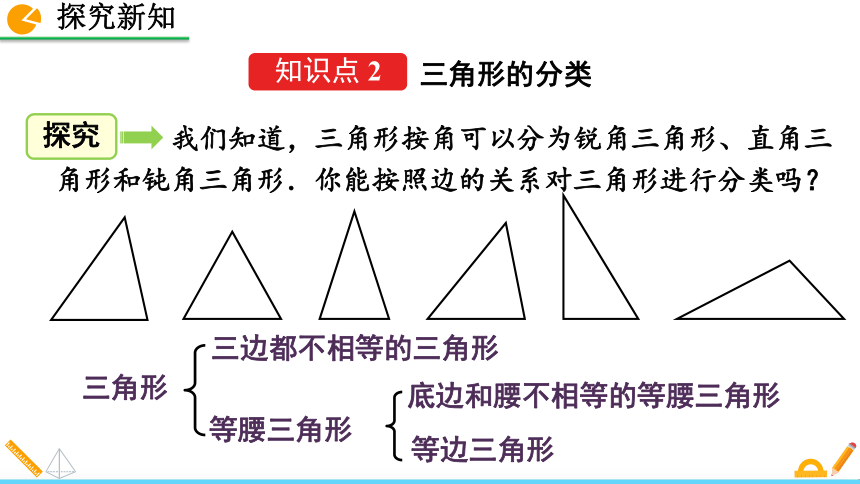
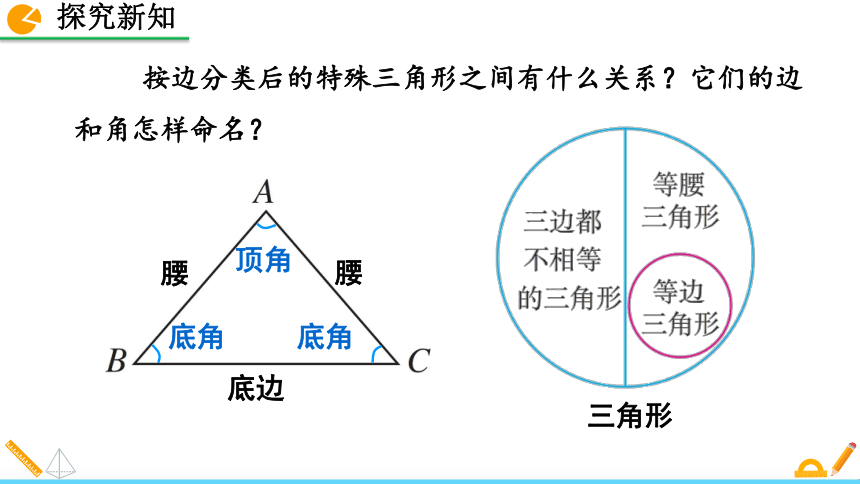
△BCE. 我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?三边都不相等的三角形 三角形 等腰三角形 底边和腰不相等的等腰三角形 等边三角形 三角形的分类按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?腰腰底边三角形 顶角底角底角判断三角形的形状例2 根据下列条件,判断△ABC的形状.
①∠A=45°,∠B=65°,∠C=70°;
②∠C=110°; ③∠C=90°; ④AB=BC=3,AC=4解:①∵∠A,∠B,∠C都小于90°,
∴△ABC是锐角三角形
②∵∠C=110°>90°,∴△ABC是钝角三角形
③∵∠C=90°=90°, ∴△ABC是直角三角形
④∵AB=BC=3,AC=4,∴△ABC是等腰三角形2.下列说法正确的有( ).
①等腰三角形是等边三角形;
②三角形按边可分为等腰三角形、等边三角形和不等
边三角形;
③等腰三角形至少有两边相等;
④三角形按角可分为锐角三角形、直角三角形和钝角
三角形.
A.①② B.①③④ C.③④ D.①②④C 在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?如果小狗在C点呢?BCACAB三角形三边的关系 在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?BCA 计算三角形的任意两边之差,并与第三边比较,你能得到什么结论?ACB试一试 如图三角形中,假设小狗要从点B出发沿着三角形的边跑到点C,它有几条路线
可以选择?各条路线的长一样吗?ABC路线1:由点B到点C.路线2:由点B到点A,再由点A到点C.两条路线长分别是BC,AB+AC.由“两点之间,线段最短”可以得到AB+AC>BC .
由不等式的基本性质可得:AB>BC–AC.ABC同理可得:AC+BC>AB, AB+BC>AC(AC>AB –BC,BC>AC–AB)三角形的三边有这样的关系:
(1) 三角形两边的和大于第三边.
(2) 三角形两边的差小于第三边.例3 下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm, 所以这三条线段不能组成一个三角形. (4) 因为4cm+5cm>6cm,所以这三条线段能组成一个三角形.利用三角形三边的关系判断三条线段能否组成三角形 只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形. 方法点拨(3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.(1)任何三条线段都能组成一个三角形 . ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形. ( )(4)已知等腰三角形的两边长分别为8cm,3cm,则这三
角形的周长为 ( ). A. 14cm B.19cm
C. 14cm或19cm D. 不确定 ××2B3.完成下列各题:例4 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?利用三角形三边的关系解决实际问题解 :(1)设各边的长为x厘米,则腰长为2x厘米,
由题意得:x+2x+2x=18
解得x=3.6 ,
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
例4 用一根长为18厘米的细铁丝围成一个等腰三角形.
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?? 有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!提示:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿的长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多. 4.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=______________.5 .如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.5, 5, 85, 8, 818cm或21cm4,4,94,9,9×√4+9+9=2222cm三边长三边长√√1. (2018?长沙)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm B.8cm,8cm,15c
C.5cm,5cm,10cm D.6cm,7cm,14cm2. (2018?常德)已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11解析:设三角形第三边的长为x,由题意得:7–3<x<7+3,
4<x<10.BC基础巩固题 1. (2018?柳州)如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个2. (2018?福建)下列各组数中,能作为一个三角形三边边长的是( )
A.1,1,2 B.1,2,4
C.2,3,4 D.2,3,5CC3.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个B 基础巩固题7 或8.5 一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm. 等腰三角形的周长为20厘米.
(1)若已知腰长是底长的2倍,求各边的长;
(2)若已知一边长为6厘米,求其他两边的长.
解:(1)设底边长为x厘米,则腰长为2x 厘米.
x + 2x + 2x = 20, 解得 x = 4.
所以三边长分别为4cm,8cm,8cm.
(2)如果6 厘米长的边为底边,设腰长为x 厘米,则6 + 2x = 20,解得x = 7;
如果6厘米长的边为腰,设底边长为x 厘米,则2×6 + x = 20,解得x = 8.
由以上讨论可知,其他两边的长分别为7 厘米,7 厘米或6 厘米,8 厘米.三角形概念分类性质三角形两边的和大于第三边.三角形两边的差小于第三边.边、顶点、内角按边分按角分(直角、锐角、钝角)三角形1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.课后作业
11.1.1 三角形的边人教版 数学 八年级 上册观察与思考1. 你能从中找出4个不同的三角形吗?与同学交流各自找出的三角形。 2. 这些三角形有什么共同
特点?EDEFGABC3. 培养学生的观察、分析、比较、操作能力,进一步发展空间观念,提高学生的探索能力.
1. 掌握三角形的有关概念,会用符号表示三角形,会对三角形进行分类.2. 理解“三角形中任意两边的和大于第三边”的含义,并能运用它解决简单的实际问题.素养目标三角形的有关概念 三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗? 由不在同一条直线上的三条线段首尾顺次连接所组成的图形,叫做三角形.
所以,三角形的特征有:
(1)三条线段;(2)不在同一直线上;(3)首尾顺次连接.三角形的定义 边c边b边a顶点A顶点B顶点C角角角①边:组成三角形的每条线段叫做三角形的边.
②顶点:每两条线段的交点叫做三角形的顶点.③内角:相邻两边组成的角.三角形的表示:三角形用符号“△”表示.记作“△ ABC”读作“三角形ABC”.如图:线段AB、BC、CA是△ABC的三边;点A、B、C△ABC的三个顶点;∠A、∠B、∠C是△ABC的三个内角.例1 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角.三角形的识别解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E. 在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.1.读出图中的各个三角形.解:△ABE,
△BCD,
△ABC,
△DCE,
△BCE. 我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.你能按照边的关系对三角形进行分类吗?三边都不相等的三角形 三角形 等腰三角形 底边和腰不相等的等腰三角形 等边三角形 三角形的分类按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?腰腰底边三角形 顶角底角底角判断三角形的形状例2 根据下列条件,判断△ABC的形状.
①∠A=45°,∠B=65°,∠C=70°;
②∠C=110°; ③∠C=90°; ④AB=BC=3,AC=4解:①∵∠A,∠B,∠C都小于90°,
∴△ABC是锐角三角形
②∵∠C=110°>90°,∴△ABC是钝角三角形
③∵∠C=90°=90°, ∴△ABC是直角三角形
④∵AB=BC=3,AC=4,∴△ABC是等腰三角形2.下列说法正确的有( ).
①等腰三角形是等边三角形;
②三角形按边可分为等腰三角形、等边三角形和不等
边三角形;
③等腰三角形至少有两边相等;
④三角形按角可分为锐角三角形、直角三角形和钝角
三角形.
A.①② B.①③④ C.③④ D.①②④C 在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?如果小狗在C点呢?BCACAB三角形三边的关系 在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?BCA 计算三角形的任意两边之差,并与第三边比较,你能得到什么结论?ACB试一试 如图三角形中,假设小狗要从点B出发沿着三角形的边跑到点C,它有几条路线
可以选择?各条路线的长一样吗?ABC路线1:由点B到点C.路线2:由点B到点A,再由点A到点C.两条路线长分别是BC,AB+AC.由“两点之间,线段最短”可以得到AB+AC>BC .
由不等式的基本性质可得:AB>BC–AC.ABC同理可得:AC+BC>AB, AB+BC>AC(AC>AB –BC,BC>AC–AB)三角形的三边有这样的关系:
(1) 三角形两边的和大于第三边.
(2) 三角形两边的差小于第三边.例3 下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm, 所以这三条线段不能组成一个三角形. (4) 因为4cm+5cm>6cm,所以这三条线段能组成一个三角形.利用三角形三边的关系判断三条线段能否组成三角形 只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形. 方法点拨(3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.(1)任何三条线段都能组成一个三角形 . ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形. ( )(4)已知等腰三角形的两边长分别为8cm,3cm,则这三
角形的周长为 ( ). A. 14cm B.19cm
C. 14cm或19cm D. 不确定 ××2B3.完成下列各题:例4 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?利用三角形三边的关系解决实际问题解 :(1)设各边的长为x厘米,则腰长为2x厘米,
由题意得:x+2x+2x=18
解得x=3.6 ,
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
例4 用一根长为18厘米的细铁丝围成一个等腰三角形.
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?? 有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!提示:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿的长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多. 4.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=______________.5 .如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.5, 5, 85, 8, 818cm或21cm4,4,94,9,9×√4+9+9=2222cm三边长三边长√√1. (2018?长沙)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm B.8cm,8cm,15c
C.5cm,5cm,10cm D.6cm,7cm,14cm2. (2018?常德)已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11解析:设三角形第三边的长为x,由题意得:7–3<x<7+3,
4<x<10.BC基础巩固题 1. (2018?柳州)如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个2. (2018?福建)下列各组数中,能作为一个三角形三边边长的是( )
A.1,1,2 B.1,2,4
C.2,3,4 D.2,3,5CC3.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个B 基础巩固题7 或8.5 一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm. 等腰三角形的周长为20厘米.
(1)若已知腰长是底长的2倍,求各边的长;
(2)若已知一边长为6厘米,求其他两边的长.
解:(1)设底边长为x厘米,则腰长为2x 厘米.
x + 2x + 2x = 20, 解得 x = 4.
所以三边长分别为4cm,8cm,8cm.
(2)如果6 厘米长的边为底边,设腰长为x 厘米,则6 + 2x = 20,解得x = 7;
如果6厘米长的边为腰,设底边长为x 厘米,则2×6 + x = 20,解得x = 8.
由以上讨论可知,其他两边的长分别为7 厘米,7 厘米或6 厘米,8 厘米.三角形概念分类性质三角形两边的和大于第三边.三角形两边的差小于第三边.边、顶点、内角按边分按角分(直角、锐角、钝角)三角形1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.课后作业
