11.2.1 三角形的内角课件(共两课时,65张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角课件(共两课时,65张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 09:51:46 | ||
图片预览





文档简介
课件65张PPT。11.2 与三角形有关的角
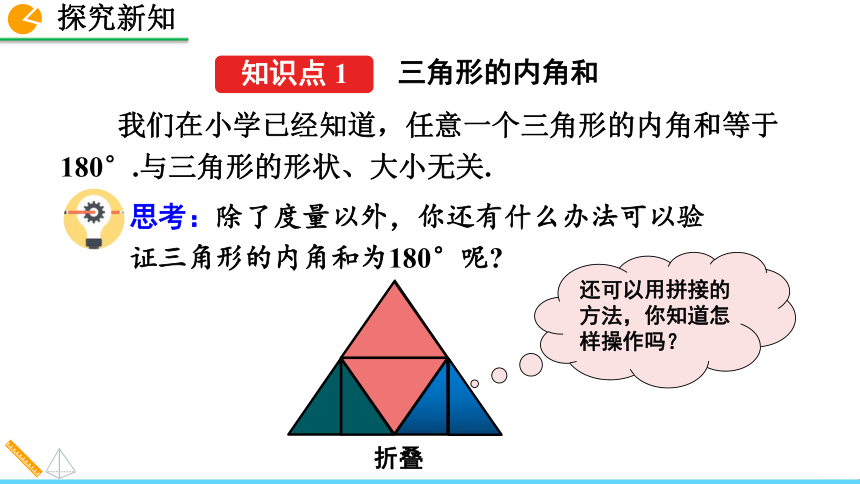
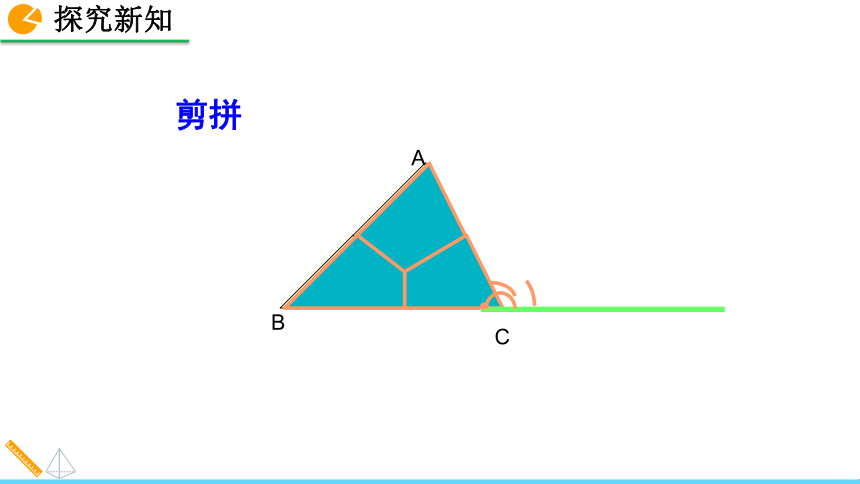
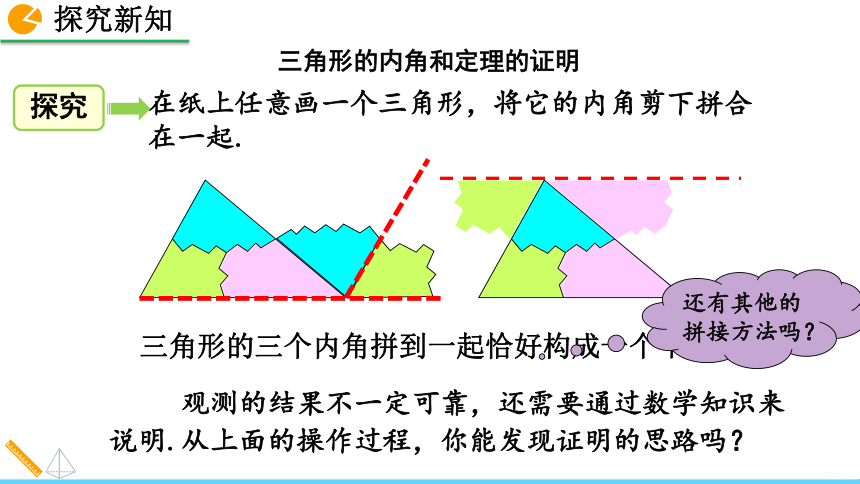
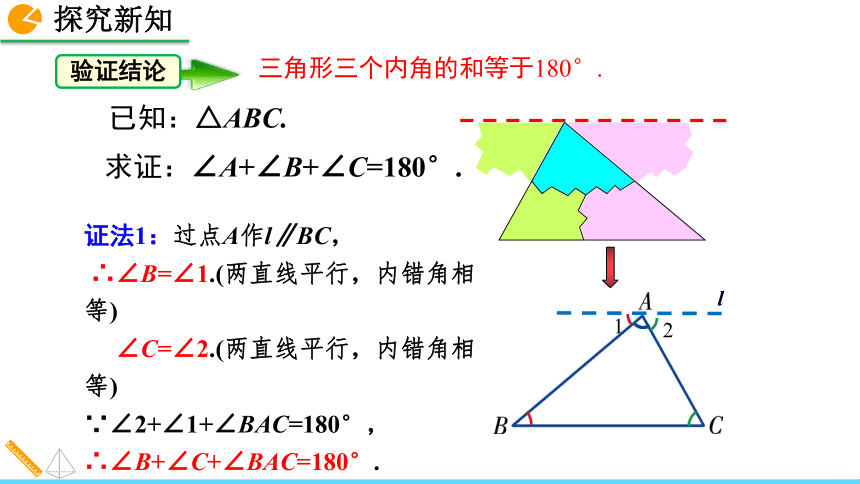
11.2.1 三角形的内角第一课时第二课时人教版 数学 八年级 上册第一课时三角形的内角和我的形状最小,那我的内角和最小.我的形状最大,那我的内角和最大.不对,我有一个钝角,所以我的内角和才是最大的. 一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.2. 会运用三角形内角和定理进行计算.1. 会用平行线的性质与平角的定义证明三角形内角和等于180°. 我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?折叠还可以用拼接的方法,你知道怎样操作吗?三角形的内角和剪拼测量480720600600+480+720=1800锐角三角形三角形的三个内角拼到一起恰好构成一个平角. 观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?三角形的内角和定理的证明在纸上任意画一个三角形,将它的内角剪下拼合在一起.还有其他的拼接方法吗?验证结论三角形三个内角的和等于180°.求证:∠A+∠B+∠C=180°.已知:△ABC.证法1:过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
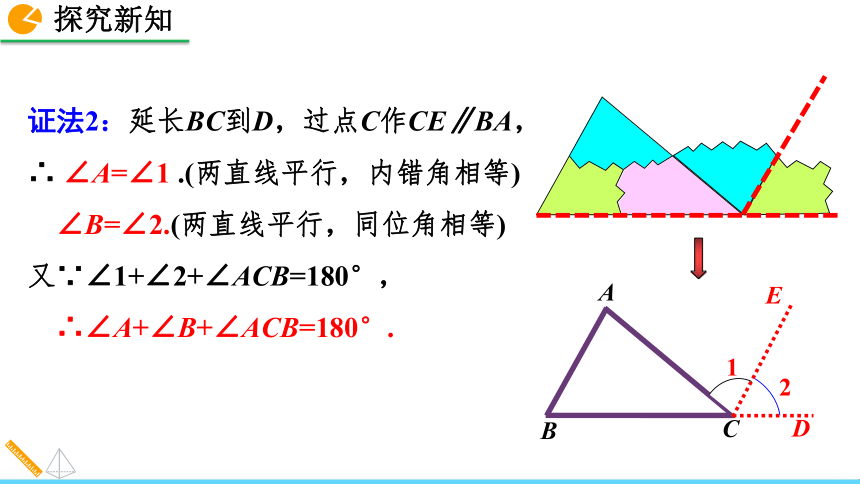
∴∠B+∠C+∠BAC=180°.12证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.EDEDF证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
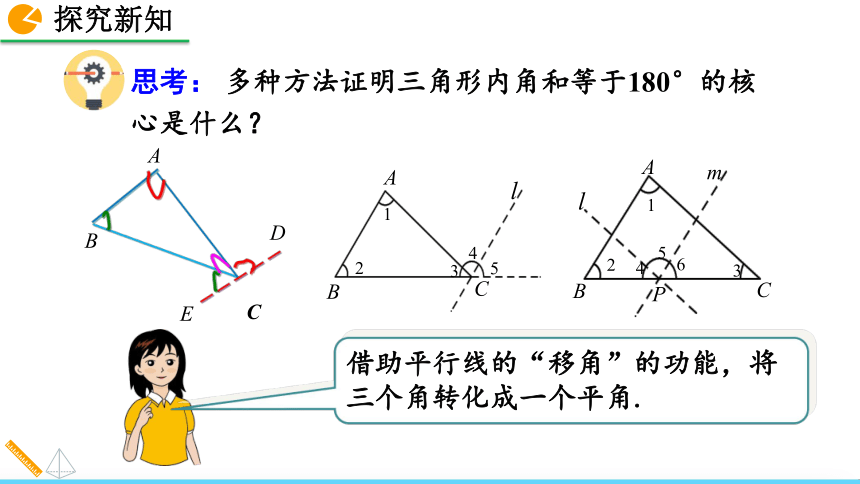
∴∠A+∠B+∠C=180°.同学们还有其他的方法吗?思考: 多种方法证明三角形内角和等于180°的核心是什么?借助平行线的“移角”的功能,将三个角转化成一个平角.同学们按照上图中的辅助线,给出证明步骤.试一试 为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.思路总结 为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.作辅助线例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, AD是△ABC的角平分线,求∠ADB的度数.解:由∠BAC=40 °, AD是△ABC的角平分线,得∠BAD= ∠BAC=20 °.在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.利用三角形的内角和定理求角的度数 如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.解:∵∠A=50°,∠B=70°,
∴∠ACB=180°–∠A–∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°–∠B –∠BCD=80°.2.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A = 150°,∠B= ∠D=40°.求∠C的度数.解:∠C=180°×2–(40°+40°+150°)
=130°.1. 在△ABC中,∠B=40°,∠C=80°,则∠A的度数为( )
A.30° B.40° C.50° D.60°D3.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的大小是( )
A.45° B.54° C.40° D.50°C例2 如图,△ABC中,D在BC的延长线上,过D作
DE⊥AB于E,交AC于F.
已知∠A=30°,∠FCD=80°,求∠D.解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°–∠FEA–∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°–∠CFD–∠FCD=40°.?4. 直线l1∥l2,一块含45°角的直角三角尺如图放置,∠1=85°,
则∠2=________.40°基本图形由三角形的内角和定理易得
∠A+∠B=∠C+∠D.由三角形的内角和定理易得∠1+∠2=∠3+∠4. 归纳总结例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有3x + x +(x + 15)= 180.解得 x = 33.所以 3x = 99 , x + 15 = 48.答: ∠A, ∠B, ∠C的度数分别为99°, 33°,48°.几何问题借助方程来解. 这是一个重要的数学思想.方程的思想与三角形内角和定理的综合应用 在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数. 解析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.比例关系可考虑用方程思想求角度.解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°–90°–30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD–∠ACE=60°–45°=15°.②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 . ①在△ABC中,∠A=35°,∠ B=43 °,则∠ C= . ③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .102°直角60°50°70°5.完成下列各题.解析:设∠A=x,∠B=2x,∠C=3x,由三角形的内角和定理得:x+2x+3x=180°,解得x=30°,3x=90°.例4 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、
B两岛的视角∠ACB是多少度?利用三角形的内角和定理解决实际问题(方位问题).解: ∠CAB= ∠BAD– ∠CAD=80 °– 50°=30°.由AD//BE,得∠BAD+ ∠ABE=180 °.所以∠ABE=180 °– ∠BAD=180°–80°=100°,
∠ABC= ∠ABE– ∠EBC=100°–40°=60°.在△ABC中,
∠ACB =180 °– ∠ABC– ∠ CAB
=180°–60°–30° =90°,答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°. 如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.解:如图,由题意得BE∥AD,∠BAD=40°,
∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∠BAC=40°+15°=55°,
∴∠CBA=∠EBC–∠EBA=80°–40°=40°,
∴∠ACB=180°–∠BAC–∠ABC
=180°–55°–40°=85°.DE6.如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C处时的视角∠BAC是多少度?解:∵在B处测得灯塔A在北偏东60°的方向,
∴ ∠ABD=60°.
又∵ ∠DBE=90°,
∴ ∠ABE=90°–∠ABD=90°–60°=30°.
∵在C处测得灯塔A在北偏东40°的方向,
∴ ∠ACE=90°–40°=50°.
∴ ∠BAC=∠ACE–∠ABE=50°–30°=20°.
即在灯塔A处观看B和C处时的视角∠BAC是20°. (2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°?C1.求出下列各图中的x值.x=70 x=60x=30 x=50 3. 如图,则∠1+∠2+∠3+∠4=___________ .280 °2.(2018?滨州)在△ABC中,若∠A=30°,∠B=50°,则∠C= .100°1. 如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°–(∠CED+∠C)
=180°–(78°+60°)
=42°.2.如图,在△ABC中,∠B=42°,∠C=78°,AD平分∠BAC.求∠ADC的度数.解:∵∠B=42°,∠C=78°,
∴∠BAC=180°–∠B –∠C=60°.
∵AD平分∠BAC,
∴∠CAD= ∠BAC=30°,
∴∠ADC=180°–∠B–∠CAD=72°.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°–60°=120°.你能直接写出∠BPC与∠A 之间的数量关系吗?解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°– (∠ABC+∠ACB)
=180°– (180°–∠A)=90°+ ∠A .求角度证法应用转化为一个平角
或同旁内角互补辅助线三角形的内角和等于180 °作平行线
转化思想第二课时直角三角形 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.你知道其中的道理吗?内角三兄弟之争 老大的度数为90°,老二若是比老大的度数大,那么老二的度数要大于90°,而三角形的内角和为180°,相互矛盾,因而是不可能的.在这个家里,我是永远的老大.3. 会运用直角三角形的性质和判定进行相关计算.1. 了解直角三角形两个锐角的关系.2. 掌握直角三角形的判定. 如下图所示是我们常用的三角板,两锐角的度数之和为多少度?直角三角形的两个锐角互余问题1: 如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢? 在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得
∠A +∠B+∠C=90°,
即 ∠A +∠B=90°.由此,你可以得到直角三角形有什么性质呢?问题2:直角三角形的两个锐角互余.(直角三角形的性质定理) 应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC . 归纳总结方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.例1(1)如图?,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?图?利用直角三角形的性质证明角相等或求角的度数解:∠A=∠C.
理由如下:
∵∠B=∠D=90°,
∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠C.(2)如图?,∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.图?与图?有哪些共同点与不同点?1. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.120° B.90° C.60° D.30° D2. 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.70 B.65
C.60 D.55A例2 如图, ∠C=∠D=90 °, AD, BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?解:在Rt△ACE中,
∠CAE=90 °– ∠AEC. 在Rt△BDE中,
∠DBE=90 °– ∠BED. ∵ ∠AEC= ∠BED,
∴ ∠CAE= ∠DBE.解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°. 如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?3. 如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.解:∵CD是AB上的高,
∴∠DBC=90°–∠DCB=90°–45°=45°.
∵BE是AC上的高,
∴∠EBC=90°–∠ECB=90°–67°=23°.
∴∠ABE=∠ABC–∠EBC=45°–23°=22°.思考:通过前面的例题,你能画出这些题型的基本图形吗?基本图形∠A=∠C∠A=∠D 归纳总结有两个角互余的三角形是直角三角形吗? 如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗? 在△ABC中,
因为 ∠A +∠B +∠C=180°,
又 ∠A +∠B=90°,
所以∠C=90°.
即△ABC是直角三角形.有两个角互余的三角形是直角三角形ABC应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形. 有两个角互余的三角形是直角三角形. (直角三角形的性质定理) 归纳总结例3 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?解:在Rt△ABC中,
∠2+ ∠A=90 °. ∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.即△ADE是直角三角形.利用直角三角形的判定定理识别直角三角形4.已知∠A=37°,∠B=53°,则△ABC为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上都有可能 C5.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ∠B= ∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=2∠B=3∠CD例4 如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.6. 如图,BD平分∠ABC,∠ADB=60°,∠BDC=80°,∠C=70°.试判断△ABD的形状.解:在△DBC中,∠DBC=180°–∠BDC–∠C
=180°–80°–70°=30°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°.
在△ABD中,
∵∠ADB+∠ABD=60°+30°=90°,
∴△ABD是直角三角形. (2018?永州)一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC=_________. 解析:∵∠CEA=60°,∠BAE=45°,
∴∠ADE=180°–∠CEA–∠BAE=75°,
∴∠BDC=∠ADE=75°.75°1. 如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.90°2. 如图,AB、CD相交于点O,AC⊥CD于点C, 若∠BOD=38°,则∠A=________.52°第1题图第2题图3. 在△ABC中,若∠A=43°,∠B=47°,则这个
三角形是____________.直角三角形4.在一个直角三角形中,有一个锐角等于40°,则另 一个锐角的度数是( )
A.40° B.50° C.60° D.70° B5. 具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A–∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C D 如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B B.∠A
C.∠BCD和∠A D.∠BCD C 如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.直角三角形的性质与判定性质直角三角形的两个锐角互余判定有两个角互余的三角形是直角三角形1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.
11.2.1 三角形的内角第一课时第二课时人教版 数学 八年级 上册第一课时三角形的内角和我的形状最小,那我的内角和最小.我的形状最大,那我的内角和最大.不对,我有一个钝角,所以我的内角和才是最大的. 一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.2. 会运用三角形内角和定理进行计算.1. 会用平行线的性质与平角的定义证明三角形内角和等于180°. 我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?折叠还可以用拼接的方法,你知道怎样操作吗?三角形的内角和剪拼测量480720600600+480+720=1800锐角三角形三角形的三个内角拼到一起恰好构成一个平角. 观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?三角形的内角和定理的证明在纸上任意画一个三角形,将它的内角剪下拼合在一起.还有其他的拼接方法吗?验证结论三角形三个内角的和等于180°.求证:∠A+∠B+∠C=180°.已知:△ABC.证法1:过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.12证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.EDEDF证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.同学们还有其他的方法吗?思考: 多种方法证明三角形内角和等于180°的核心是什么?借助平行线的“移角”的功能,将三个角转化成一个平角.同学们按照上图中的辅助线,给出证明步骤.试一试 为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.思路总结 为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.作辅助线例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, AD是△ABC的角平分线,求∠ADB的度数.解:由∠BAC=40 °, AD是△ABC的角平分线,得∠BAD= ∠BAC=20 °.在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.利用三角形的内角和定理求角的度数 如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.解:∵∠A=50°,∠B=70°,
∴∠ACB=180°–∠A–∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°–∠B –∠BCD=80°.2.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A = 150°,∠B= ∠D=40°.求∠C的度数.解:∠C=180°×2–(40°+40°+150°)
=130°.1. 在△ABC中,∠B=40°,∠C=80°,则∠A的度数为( )
A.30° B.40° C.50° D.60°D3.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的大小是( )
A.45° B.54° C.40° D.50°C例2 如图,△ABC中,D在BC的延长线上,过D作
DE⊥AB于E,交AC于F.
已知∠A=30°,∠FCD=80°,求∠D.解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°–∠FEA–∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°–∠CFD–∠FCD=40°.?4. 直线l1∥l2,一块含45°角的直角三角尺如图放置,∠1=85°,
则∠2=________.40°基本图形由三角形的内角和定理易得
∠A+∠B=∠C+∠D.由三角形的内角和定理易得∠1+∠2=∠3+∠4. 归纳总结例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有3x + x +(x + 15)= 180.解得 x = 33.所以 3x = 99 , x + 15 = 48.答: ∠A, ∠B, ∠C的度数分别为99°, 33°,48°.几何问题借助方程来解. 这是一个重要的数学思想.方程的思想与三角形内角和定理的综合应用 在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数. 解析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.比例关系可考虑用方程思想求角度.解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°–90°–30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD–∠ACE=60°–45°=15°.②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 . ①在△ABC中,∠A=35°,∠ B=43 °,则∠ C= . ③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .102°直角60°50°70°5.完成下列各题.解析:设∠A=x,∠B=2x,∠C=3x,由三角形的内角和定理得:x+2x+3x=180°,解得x=30°,3x=90°.例4 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、
B两岛的视角∠ACB是多少度?利用三角形的内角和定理解决实际问题(方位问题).解: ∠CAB= ∠BAD– ∠CAD=80 °– 50°=30°.由AD//BE,得∠BAD+ ∠ABE=180 °.所以∠ABE=180 °– ∠BAD=180°–80°=100°,
∠ABC= ∠ABE– ∠EBC=100°–40°=60°.在△ABC中,
∠ACB =180 °– ∠ABC– ∠ CAB
=180°–60°–30° =90°,答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°. 如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.解:如图,由题意得BE∥AD,∠BAD=40°,
∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∠BAC=40°+15°=55°,
∴∠CBA=∠EBC–∠EBA=80°–40°=40°,
∴∠ACB=180°–∠BAC–∠ABC
=180°–55°–40°=85°.DE6.如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C处时的视角∠BAC是多少度?解:∵在B处测得灯塔A在北偏东60°的方向,
∴ ∠ABD=60°.
又∵ ∠DBE=90°,
∴ ∠ABE=90°–∠ABD=90°–60°=30°.
∵在C处测得灯塔A在北偏东40°的方向,
∴ ∠ACE=90°–40°=50°.
∴ ∠BAC=∠ACE–∠ABE=50°–30°=20°.
即在灯塔A处观看B和C处时的视角∠BAC是20°. (2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°?C1.求出下列各图中的x值.x=70 x=60x=30 x=50 3. 如图,则∠1+∠2+∠3+∠4=___________ .280 °2.(2018?滨州)在△ABC中,若∠A=30°,∠B=50°,则∠C= .100°1. 如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°–(∠CED+∠C)
=180°–(78°+60°)
=42°.2.如图,在△ABC中,∠B=42°,∠C=78°,AD平分∠BAC.求∠ADC的度数.解:∵∠B=42°,∠C=78°,
∴∠BAC=180°–∠B –∠C=60°.
∵AD平分∠BAC,
∴∠CAD= ∠BAC=30°,
∴∠ADC=180°–∠B–∠CAD=72°.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°–60°=120°.你能直接写出∠BPC与∠A 之间的数量关系吗?解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°– (∠ABC+∠ACB)
=180°– (180°–∠A)=90°+ ∠A .求角度证法应用转化为一个平角
或同旁内角互补辅助线三角形的内角和等于180 °作平行线
转化思想第二课时直角三角形 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.你知道其中的道理吗?内角三兄弟之争 老大的度数为90°,老二若是比老大的度数大,那么老二的度数要大于90°,而三角形的内角和为180°,相互矛盾,因而是不可能的.在这个家里,我是永远的老大.3. 会运用直角三角形的性质和判定进行相关计算.1. 了解直角三角形两个锐角的关系.2. 掌握直角三角形的判定. 如下图所示是我们常用的三角板,两锐角的度数之和为多少度?直角三角形的两个锐角互余问题1: 如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢? 在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得
∠A +∠B+∠C=90°,
即 ∠A +∠B=90°.由此,你可以得到直角三角形有什么性质呢?问题2:直角三角形的两个锐角互余.(直角三角形的性质定理) 应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC . 归纳总结方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.例1(1)如图?,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?图?利用直角三角形的性质证明角相等或求角的度数解:∠A=∠C.
理由如下:
∵∠B=∠D=90°,
∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠C.(2)如图?,∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.图?与图?有哪些共同点与不同点?1. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.120° B.90° C.60° D.30° D2. 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.70 B.65
C.60 D.55A例2 如图, ∠C=∠D=90 °, AD, BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?解:在Rt△ACE中,
∠CAE=90 °– ∠AEC. 在Rt△BDE中,
∠DBE=90 °– ∠BED. ∵ ∠AEC= ∠BED,
∴ ∠CAE= ∠DBE.解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°. 如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?3. 如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.解:∵CD是AB上的高,
∴∠DBC=90°–∠DCB=90°–45°=45°.
∵BE是AC上的高,
∴∠EBC=90°–∠ECB=90°–67°=23°.
∴∠ABE=∠ABC–∠EBC=45°–23°=22°.思考:通过前面的例题,你能画出这些题型的基本图形吗?基本图形∠A=∠C∠A=∠D 归纳总结有两个角互余的三角形是直角三角形吗? 如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗? 在△ABC中,
因为 ∠A +∠B +∠C=180°,
又 ∠A +∠B=90°,
所以∠C=90°.
即△ABC是直角三角形.有两个角互余的三角形是直角三角形ABC应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形. 有两个角互余的三角形是直角三角形. (直角三角形的性质定理) 归纳总结例3 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?解:在Rt△ABC中,
∠2+ ∠A=90 °. ∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.即△ADE是直角三角形.利用直角三角形的判定定理识别直角三角形4.已知∠A=37°,∠B=53°,则△ABC为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上都有可能 C5.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ∠B= ∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=2∠B=3∠CD例4 如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.6. 如图,BD平分∠ABC,∠ADB=60°,∠BDC=80°,∠C=70°.试判断△ABD的形状.解:在△DBC中,∠DBC=180°–∠BDC–∠C
=180°–80°–70°=30°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°.
在△ABD中,
∵∠ADB+∠ABD=60°+30°=90°,
∴△ABD是直角三角形. (2018?永州)一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC=_________. 解析:∵∠CEA=60°,∠BAE=45°,
∴∠ADE=180°–∠CEA–∠BAE=75°,
∴∠BDC=∠ADE=75°.75°1. 如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.90°2. 如图,AB、CD相交于点O,AC⊥CD于点C, 若∠BOD=38°,则∠A=________.52°第1题图第2题图3. 在△ABC中,若∠A=43°,∠B=47°,则这个
三角形是____________.直角三角形4.在一个直角三角形中,有一个锐角等于40°,则另 一个锐角的度数是( )
A.40° B.50° C.60° D.70° B5. 具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A–∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C D 如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B B.∠A
C.∠BCD和∠A D.∠BCD C 如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.直角三角形的性质与判定性质直角三角形的两个锐角互余判定有两个角互余的三角形是直角三角形1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.
