11.3.2 多边形的内角和课件(40张PPT)
文档属性
| 名称 | 11.3.2 多边形的内角和课件(40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 10:00:06 | ||
图片预览







文档简介
课件40张PPT。11.3 多边形及其内角和
11.3.2 多边形的内角和人教版 数学 八年级 上册思考:你知道正六边形的内角和是多少吗?1. 能通过不同方法探索多边形的内角和与外角和公式.2. 能运用多边形的内角和公式与外角和公式解决问题.素养目标你知道长方形和正方形的内角和是多少 度?
三角形内角和是多少度?三角形内角和是180°.都是360°.猜想任意四边形的内角和是多少度?
多边形的内角和问题1:问题2:问题3:猜想:四边形ABCD的内角和是360°.你能用以前学过的知识说明一下你的结论吗?解法一:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
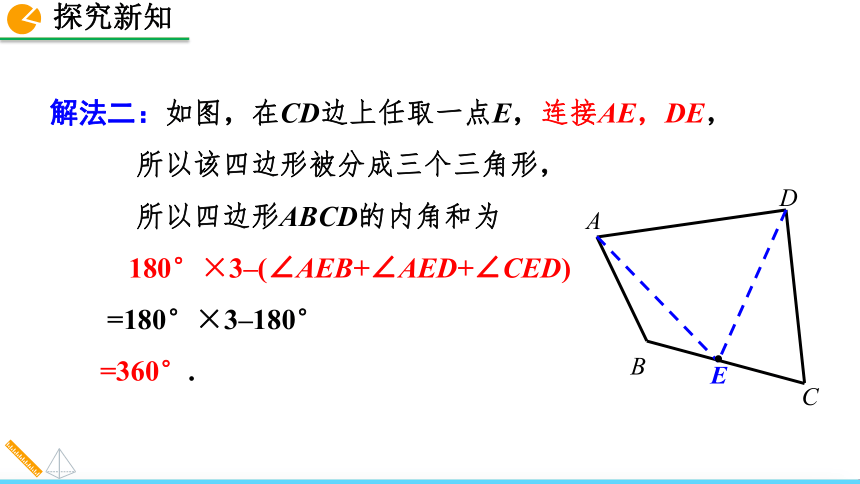
180°×2=360°.猜想与证明问题4:解法二:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3–(∠AEB+∠AED+∠CED)
=180°×3–180°
=360°.
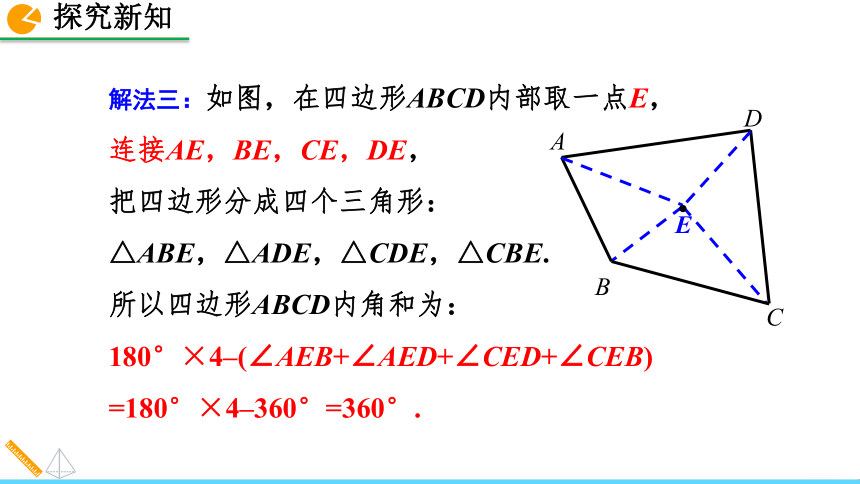
E解法三:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4–(∠AEB+∠AED+∠CED+∠CEB)
=180°×4–360°=360°.EP解法四:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.所以四边形ABCD内角和为180°×3 –180°= 360°.这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.结论: 四边形的内角和为360°.例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.解:
如图,四边形ABCD中,∠A+ ∠C =180°.∠A+∠B+∠C+∠D=(4–2) ×180 °= 360 °,因为
∠B+∠D= 360°–(∠A+∠C)
= 360°– 180° =180°.所以
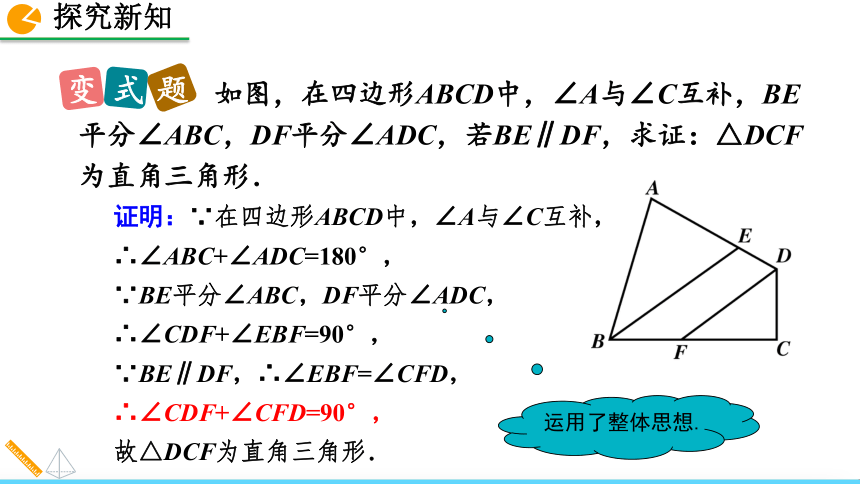
如果一个四边形的一组对角互补,那么另一组对角互补.运用四边形内角和定理进行证明 如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
故△DCF为直角三角形.运用了整体思想.1. 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.解:连接BE.∵∠DOB=∠C+∠D,
∠DOB=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
∵在四边形ABEF中,
∠A+∠ABE+∠BEF+∠F=(4–2)×180°=360°,
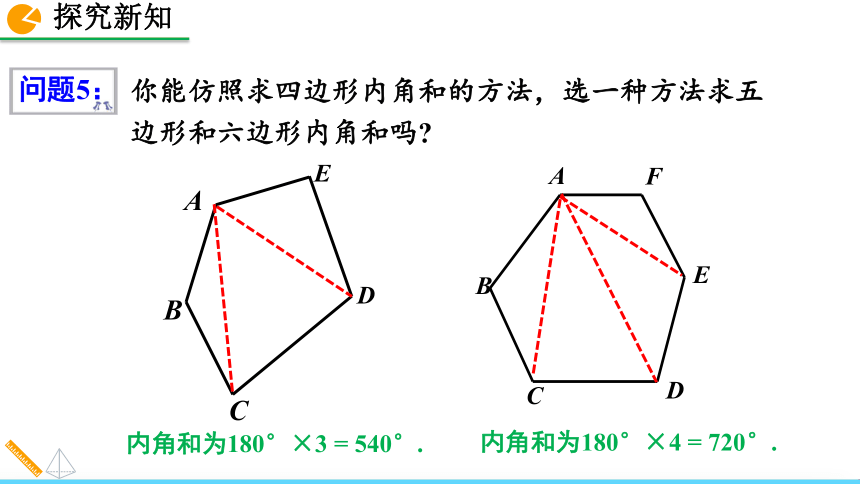
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.你能仿照求四边形内角和的方法,选一种方法求五
边形和六边形内角和吗? 内角和为180°×3 = 540°.内角和为180°×4 = 720°.问题5:······0n –3 1231234 n –2 ( n –2 )·180o1×180o=180o2×180o=360o 3×180o=540o4×180o=720o························由特殊到一般 分割多边形三角形分割点与多边形的位置关系顶点边上内部外部转化思想多边形的内角和公式n边形内角和等于(n–2)×180 °.注意:①n边形的内角和随边数的增加而增加,每增加一条边其内角和增加180°.②多边形的内角和是180°的整倍数. 归纳总结例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?解:设这个多边形边数为n,则
(n–2)?180=360+720,
解得n=8, ∵这个多边形的每个内角都相等,
(8–2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.利用多边形内角和公式求角度或边数2. 根据多边形的内角和完成下列题目.(1) 一个多边形的内角和是720°,这个多边形的边数是( )
A.4条 B.5条 C.6条 D.7条
(2) 若一个多边形的边数为8条,则这个多边形的内角和是( )
A.900° B.540° C.1080° D.360°
(3) 若一个多边形增加一条边,那么它的内角和( )
A.增加180° B.增加360° C.减少360° D.不变CCA例3 已知n边形的内角和θ=(n–2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;解:∵ 360°÷180°=2, 630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4;(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.解:依题意有
(n+x–2)×180°–(n–2)×180°=360°,
解得x=2.
故x的值是2. 一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?解法一:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°,
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°–1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.思路点拨:多边形的内角的度数在0°~180°之间.解法二: 1125°÷180°=6…45
6+1=7,180°×7=1260°
1260°–1125=135°
(n–2)180°=1260°,n=9.
因此,这个角是135°,这个多边形是九边形.3. 如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.解析:根据五边形的内角和等于540°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°–∠C–∠D–∠E=230°.
∵AP平分∠EAB,
∴∠PAB= ∠EAB,
同理可得∠ABP= ∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°–∠PAB–∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°. 用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
多边形的外角和 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.任意一个外角和它相邻的内角有什么关系?
五个外角加上它们分别相邻的五个内角和是多少?
互补5×180°=900°五边形外角和=360 °=5个平角–五边形内角和=5×180°–(5–2) × 180°结论:五边形的外角和等于360°.这五个平角和与五边形的内角和、外角和有什么关系? 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和n边形的外角和等于360°.–(n–2) × 180°=360 °=n个平角–n边形内角和= n×180 °思考:n边形的外角和又是多少呢?与边数无关 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?每个内角的度数是每个外角的度数是练一练:
(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.六正八例4 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n.
∵它的内角和等于 (n–2)?180°,
多边形外角和等于360°,
∴ (n–2)?180°=2× 360o.
解得 n=6.
∴这个多边形的边数为6.多边形的内角和公式和外角和公式的综合应用例5 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解法一:设这个多边形的内角为7x °,外角为2x°,
根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.
还有其他解法吗?解法二:设这个多边形的边数为n ,根据题意得解得 n=9.答:这个多边形是九边形. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.解:设该正多边形的内角是x°,外角是y°,
则得到一个方程组 解得
而任何多边形的外角和是360°,
则该正多边形的边数为360÷120=3,
故这个多边形的每个内角的度数是60°,边数是三条. 4. 如图,在正五边形ABCDE中,连接BE,求∠BED的度数.解:由题意得
AB=AE,所以∠AEB= (180°–∠A)=36°,
所以∠BED=∠AED–∠AEB=108°–36°=72°.1.(2018?宁波)已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9解析:正多边形的一个外角等于40°,且外角和为360°,则这个正多边形的边数是:360°÷40°=9.D2.(2018?宿迁)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.解析:设多边形的边数为n,根据题意,得
(n–2)?180=3×360,
解得 n=8.
则这个多边形的边数是8.81.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )2.(2018?怀化)一个多边形的每一个外角都是36°,则这个多边形的边数是 .103. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.1504. 一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A. 360° B. 540 °
C. 720 ° D. 900 °B 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.?如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.89多边形的内角和内角和计算公式(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.外角和多边形的外角和等于360°
特别注意:与边数无关.正多
边形内角= ,外角=1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.
11.3.2 多边形的内角和人教版 数学 八年级 上册思考:你知道正六边形的内角和是多少吗?1. 能通过不同方法探索多边形的内角和与外角和公式.2. 能运用多边形的内角和公式与外角和公式解决问题.素养目标你知道长方形和正方形的内角和是多少 度?
三角形内角和是多少度?三角形内角和是180°.都是360°.猜想任意四边形的内角和是多少度?
多边形的内角和问题1:问题2:问题3:猜想:四边形ABCD的内角和是360°.你能用以前学过的知识说明一下你的结论吗?解法一:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.猜想与证明问题4:解法二:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3–(∠AEB+∠AED+∠CED)
=180°×3–180°
=360°.
E解法三:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4–(∠AEB+∠AED+∠CED+∠CEB)
=180°×4–360°=360°.EP解法四:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.所以四边形ABCD内角和为180°×3 –180°= 360°.这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.结论: 四边形的内角和为360°.例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.解:
如图,四边形ABCD中,∠A+ ∠C =180°.∠A+∠B+∠C+∠D=(4–2) ×180 °= 360 °,因为
∠B+∠D= 360°–(∠A+∠C)
= 360°– 180° =180°.所以
如果一个四边形的一组对角互补,那么另一组对角互补.运用四边形内角和定理进行证明 如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
故△DCF为直角三角形.运用了整体思想.1. 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.解:连接BE.∵∠DOB=∠C+∠D,
∠DOB=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
∵在四边形ABEF中,
∠A+∠ABE+∠BEF+∠F=(4–2)×180°=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.你能仿照求四边形内角和的方法,选一种方法求五
边形和六边形内角和吗? 内角和为180°×3 = 540°.内角和为180°×4 = 720°.问题5:······0n –3 1231234 n –2 ( n –2 )·180o1×180o=180o2×180o=360o 3×180o=540o4×180o=720o························由特殊到一般 分割多边形三角形分割点与多边形的位置关系顶点边上内部外部转化思想多边形的内角和公式n边形内角和等于(n–2)×180 °.注意:①n边形的内角和随边数的增加而增加,每增加一条边其内角和增加180°.②多边形的内角和是180°的整倍数. 归纳总结例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?解:设这个多边形边数为n,则
(n–2)?180=360+720,
解得n=8, ∵这个多边形的每个内角都相等,
(8–2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.利用多边形内角和公式求角度或边数2. 根据多边形的内角和完成下列题目.(1) 一个多边形的内角和是720°,这个多边形的边数是( )
A.4条 B.5条 C.6条 D.7条
(2) 若一个多边形的边数为8条,则这个多边形的内角和是( )
A.900° B.540° C.1080° D.360°
(3) 若一个多边形增加一条边,那么它的内角和( )
A.增加180° B.增加360° C.减少360° D.不变CCA例3 已知n边形的内角和θ=(n–2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;解:∵ 360°÷180°=2, 630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4;(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.解:依题意有
(n+x–2)×180°–(n–2)×180°=360°,
解得x=2.
故x的值是2. 一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?解法一:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°,
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°–1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.思路点拨:多边形的内角的度数在0°~180°之间.解法二: 1125°÷180°=6…45
6+1=7,180°×7=1260°
1260°–1125=135°
(n–2)180°=1260°,n=9.
因此,这个角是135°,这个多边形是九边形.3. 如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.解析:根据五边形的内角和等于540°,由∠C,∠D,∠E的度数可求∠EAB+∠ABC的度数,再根据角平分线的定义可得∠PAB与∠PBA的角度和,进一步求得∠P的度数.解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°–∠C–∠D–∠E=230°.
∵AP平分∠EAB,
∴∠PAB= ∠EAB,
同理可得∠ABP= ∠ABC,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°–∠PAB–∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°. 用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
多边形的外角和 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.任意一个外角和它相邻的内角有什么关系?
五个外角加上它们分别相邻的五个内角和是多少?
互补5×180°=900°五边形外角和=360 °=5个平角–五边形内角和=5×180°–(5–2) × 180°结论:五边形的外角和等于360°.这五个平角和与五边形的内角和、外角和有什么关系? 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和n边形的外角和等于360°.–(n–2) × 180°=360 °=n个平角–n边形内角和= n×180 °思考:n边形的外角和又是多少呢?与边数无关 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?每个内角的度数是每个外角的度数是练一练:
(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.六正八例4 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n.
∵它的内角和等于 (n–2)?180°,
多边形外角和等于360°,
∴ (n–2)?180°=2× 360o.
解得 n=6.
∴这个多边形的边数为6.多边形的内角和公式和外角和公式的综合应用例5 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解法一:设这个多边形的内角为7x °,外角为2x°,
根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.
还有其他解法吗?解法二:设这个多边形的边数为n ,根据题意得解得 n=9.答:这个多边形是九边形. 一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.解:设该正多边形的内角是x°,外角是y°,
则得到一个方程组 解得
而任何多边形的外角和是360°,
则该正多边形的边数为360÷120=3,
故这个多边形的每个内角的度数是60°,边数是三条. 4. 如图,在正五边形ABCDE中,连接BE,求∠BED的度数.解:由题意得
AB=AE,所以∠AEB= (180°–∠A)=36°,
所以∠BED=∠AED–∠AEB=108°–36°=72°.1.(2018?宁波)已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9解析:正多边形的一个外角等于40°,且外角和为360°,则这个正多边形的边数是:360°÷40°=9.D2.(2018?宿迁)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_____.解析:设多边形的边数为n,根据题意,得
(n–2)?180=3×360,
解得 n=8.
则这个多边形的边数是8.81.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )2.(2018?怀化)一个多边形的每一个外角都是36°,则这个多边形的边数是 .103. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.1504. 一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A. 360° B. 540 °
C. 720 ° D. 900 °B 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.?如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.解:如图,
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.89多边形的内角和内角和计算公式(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.外角和多边形的外角和等于360°
特别注意:与边数无关.正多
边形内角= ,外角=1 . 从课后习题中选取;
2 . 完成练习册本课时的习题.
