人教版八年级数学上册第十二章12.3 角的平分线的性质课件(2课时共59张)
文档属性
| 名称 | 人教版八年级数学上册第十二章12.3 角的平分线的性质课件(2课时共59张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 00:00:00 | ||
图片预览







文档简介
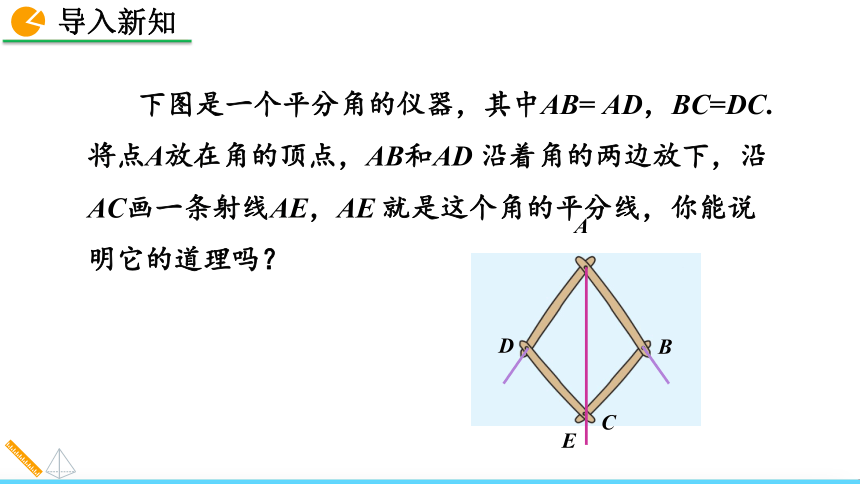
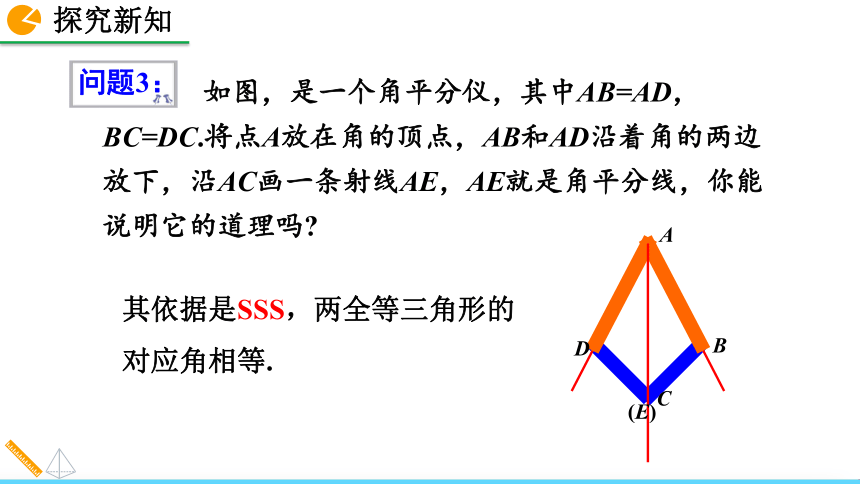
课件59张PPT。12.3 角的平分线的性质第一课时第二课时人教版 数学 八年级 上册第一课时角的平分线的性质A 下图是一个平分角的仪器,其中AB= AD,BC=DC.将点A放在角的顶点,AB和AD 沿着角的两边放下,沿AC画一条射线AE,AE 就是这个角的平分线,你能说明它的道理吗?3. 熟练地运用角平分线的性质解决实际问题. 1. 学会角平分线的画法.2. 探究并认知角平分线的性质. 在纸上画一个角,你能得到这个角的平分线吗? 用量角器度量,也可用折纸的方法. 如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?角平分线的画法问题1:问题2:提炼图形 如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?其依据是SSS,两全等三角形的
对应角相等.问题3: 如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗? 请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.提示
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢?
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
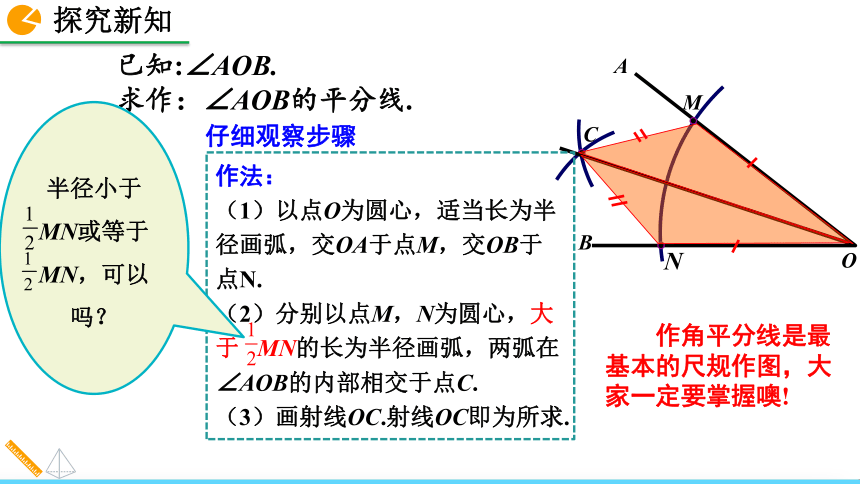
(4)你能说明为什么OC是∠AOB的平分线吗?ABO已知:∠AOB.求作:∠AOB的平分线.仔细观察步骤 作角平分线是最基本的尺规作图,大家一定要掌握噢!作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
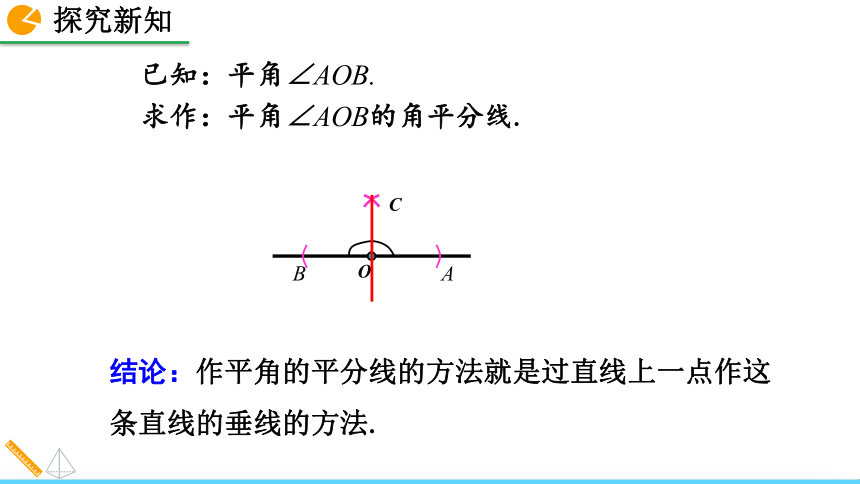
(3)画射线OC.射线OC即为所求.半径小于 MN或等于 MN,可以吗?已知:平角∠AOB.
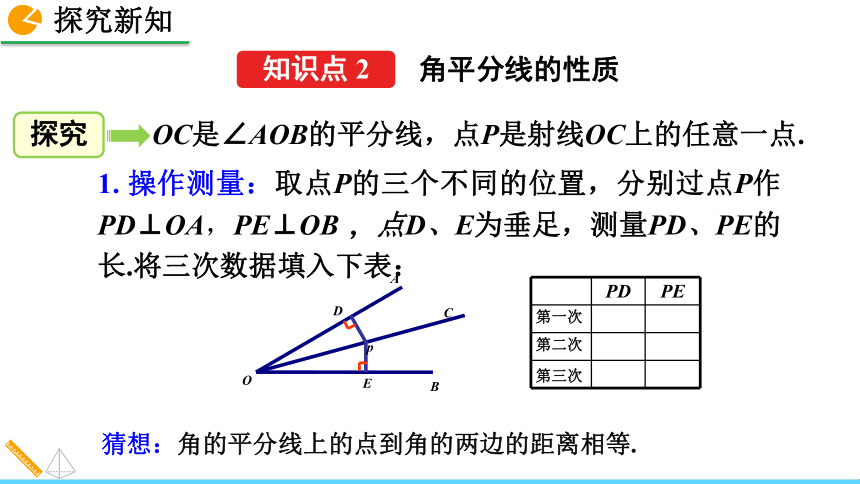
求作:平角∠AOB的角平分线.结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB ,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:2. 观察测量结果,猜想线段PD与PE的大小关系,写出结果:__________COBAPD=PE OC是∠AOB的平分线,点P是射线OC上的任意一点.猜想:角的平分线上的点到角的两边的距离相等.角平分线的性质已知:如图, ∠AOC= ∠BOC,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.证明:∵ PD⊥OA,PE⊥OB,∴ ∠PDO= ∠PEO=90 °.在△PDO和△PEO中,∠PDO= ∠PEO,∠AOC= ∠BOC,OP= OP,∴ △PDO ≌△PEO(AAS).∴PD=PE.角的平分线上的点到角的两边的距离相等.验证猜想 一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和
求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证
明过程.性质定理:角的平分线上的点到角的两边的距离相等.应用所具备的条件:定理的作用: 证明线段相等.应用格式:∵OP 是∠AOB的平分线,∴PD = PE推理的理由有三个,必须写完全,不能少了任何一个.PD⊥OA, PE⊥OB,判一判:(1)∵ 如下左图,AD平分∠BAC(已知), ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等BD CD×(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知). ∴ = ,
( ) 在角的平分线上的点到这个角的两边的距离相等BD CD×缺少“垂直距离”这一条件缺少“角平分线”这一条件例1已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.证明: ∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,∴ DE=DF, ∠DEB=∠DFC=90 °.在Rt△BDE 和 Rt△CDF中,∴ Rt△BDE ≌ Rt△CDF(HL).∴ EB=FC. 角平分线的性质的应用 如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.
求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,又∵OA=OB,OD=OD,∴△AOD≌△BOD,∴∠3=∠4,
又∵PM⊥DB,PN⊥DA,
∴PM=PN(角平分线上的点到角两边的距离相等). 如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A. PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PCD 如图,在△ABC中,∠B,∠C的平分线交于点O,OD⊥AB于点D,OE⊥AC于点E,则OD与OE的大小关系是( )
A. OD>OE B.OD=OE
C. ODPD=4cm,则PE=______cm.
4提示:存在两条垂线段——直接 应用.利用角平分线的性质求线段的长度 如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.4提示:存在一条垂线段——构造应用.1.应用角平分线性质:存在角平分线涉及距离问题2.联系角平分线性质:面积周长条件利用角平分线的性质所得到的等量关系进行转化求解(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°B?2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .3E1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .60BF3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A. SSS
B. ASA
C. AAS
D.角平分线上的点到角两边的距离相等A4. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )A.6 B.5 C.4 D.3DBCEADF6810 1. 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.解:(1)DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2)在Rt△CDB和Rt△EDB中,DC=DE,DB=DB,
∴Rt△CDB≌Rt△EDB(HL),
∴BE=BC=8.
∴ AE=AB–BE=2.
∴△AED的周长=AE+ED+DA=2+6=8.CD2.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F. 求证:CE=CF.证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF. 如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.角平分线尺规作图属于基本作图,必须熟练掌握性质定理一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等辅助线
添加过角平分线上一点向两边作垂线段为证明线段相等提供了又一途径第二课时角的平分线的判定 我们知道,角的平分线上的点到角的两边的距离相等,反过来,到角的两边的距离相等的点是否在这个角的平分线上呢?3. 学会判断一个点是否在一个角的平分线上.1. 理解角平分线判定定理.2. 掌握角平分线判定定理内容的证明方法并应用其解题.回
顾旧知ODPP到OA的距离PDP到OB的距离PE.P是角平分线上的点几何语言描述:∵ OC平分∠AOB,且PD⊥OA, PE⊥OB.∴ PD= PE.ACB角的平分线上的点到角的两边的距离相等. 叙述角平分线的性质定理.不必再证全等E 角平分线的判定角的内部到角的两边距离相等的点在角的平分线上. 交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?角平分线的性质:角的平分线上的点到角的两边的距离相等.∵ OC平分∠AOB,且PD⊥OA, PE⊥OB
∴ PD= PE几何语言:猜想:思考:这个结论正确吗?已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE. 求证:点P在∠AOB的角平分线上.证明:作射线OP, ∴点P在∠AOB 角的平分线上. 在Rt△PDO和Rt△PEO 中,(全等三角形的对应角相等). OP=OP(公共边),PD= PE(已知 ), ∵PD⊥OA,PE⊥OB.∴∠PDO=∠PEO=90°,∴Rt△PDO≌Rt△PEO( HL).∴∠AOP=∠BOP猜想证明判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.应用所具备的条件:定理的作用:判断点是否在角平分线上.应用格式:∵ PD⊥OA,PE⊥OB,PD=PE.∴点P 在∠AOB的平分线上.例1 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?DCS解:作夹角的角平分线OC,截取OD=2.5cm , D即为所求.O方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.角平分线的判定的应用1.如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,PC=3 cm,当PD=____cm时点P在∠AOB的平分线上.332.如图,AB∥CD,点P到AB,BC,CD的距离相等,则点P是 的平分线与 的平分线的交点.∠ABC∠BCD 分别画出下列三角形三个内角的平分线,你发现了什么?三角形的内角平分线发现:三角形的三条角平分线相交于一点. 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?发现:过交点作三角形三边的垂线段相等.你能证明这个结论吗?已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.D E F 证明结论 点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?点P在∠A的平分线上. 结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.D E F EO 如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和.
12BCA解:连接OC.
如图,在直角△ABC中,∠C=900,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.1.应用角平分线性质:存在角平分线涉及距离问题2.联系角平分线性质:距离面积周长条件例2 如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )A.110° B.120° C.130° D.140°A解析:由已知,O到三角形三边的距离相等,即三条角
平分线的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∠ABC+∠ACB=180°-40°=140°,
∠OBC+∠OCB=70°,
∠BOC=180°-70°=110°.利用三角形的内角平分线的性质求值 方法点拨 由已知,O 到三角形三边的距离相等,得O是三角形三条内角平分线的交点,再利用三角形内角和定理即可求出∠BOC的度数.角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定 归纳总结3.到三角形三边距离相等的点是( )
A.三边垂直平分线的交点
B.三条高所在直线的交点
C.三条角平分线的交点
D.三条中线的交点
4.如图,河南岸有一个工厂在公路西侧,工厂到公路的距离与到河岸的距离相等,并且与B的距离为300 m,在图上标出工厂的位置,并说明理由.
解:作小河与公路夹角的角平分线BM,在BM上截取BP=1.5 cm,则点P即为所求的工厂的位置C证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
又∵∠BDE=∠CDF, BE=CF,
∴△BDE≌△CDF(AAS)
∴DE=DF,
∴AD平分∠BAC.
(2019?青岛模拟)如图,已知,BE=CF,BF⊥AC于点F,DE⊥AB于点E,BF,CE交于点D.
求证:AD平分∠BAC.1. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.小区CAOBMN2. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.P 如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.E证明:∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,∴点F在∠DAE的平分线上. GHMABCFD 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置. P1P2P3P4l1l2l3角平分线
的判定定理内容角的内部到角两边距离相等的点在这个角的平分线上作用判断一个点是否在角的平分线上结论三角形的角平分线相交于内部一点 1. 从课后习题中选取;
2. 完成练习册本课时的习题.课后作业
对应角相等.问题3: 如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗? 请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.提示
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢?
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?ABO已知:∠AOB.求作:∠AOB的平分线.仔细观察步骤 作角平分线是最基本的尺规作图,大家一定要掌握噢!作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.半径小于 MN或等于 MN,可以吗?已知:平角∠AOB.
求作:平角∠AOB的角平分线.结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB ,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:2. 观察测量结果,猜想线段PD与PE的大小关系,写出结果:__________COBAPD=PE OC是∠AOB的平分线,点P是射线OC上的任意一点.猜想:角的平分线上的点到角的两边的距离相等.角平分线的性质已知:如图, ∠AOC= ∠BOC,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.证明:∵ PD⊥OA,PE⊥OB,∴ ∠PDO= ∠PEO=90 °.在△PDO和△PEO中,∠PDO= ∠PEO,∠AOC= ∠BOC,OP= OP,∴ △PDO ≌△PEO(AAS).∴PD=PE.角的平分线上的点到角的两边的距离相等.验证猜想 一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和
求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证
明过程.性质定理:角的平分线上的点到角的两边的距离相等.应用所具备的条件:定理的作用: 证明线段相等.应用格式:∵OP 是∠AOB的平分线,∴PD = PE推理的理由有三个,必须写完全,不能少了任何一个.PD⊥OA, PE⊥OB,判一判:(1)∵ 如下左图,AD平分∠BAC(已知), ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等BD CD×(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知). ∴ = ,
( ) 在角的平分线上的点到这个角的两边的距离相等BD CD×缺少“垂直距离”这一条件缺少“角平分线”这一条件例1已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.证明: ∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,∴ DE=DF, ∠DEB=∠DFC=90 °.在Rt△BDE 和 Rt△CDF中,∴ Rt△BDE ≌ Rt△CDF(HL).∴ EB=FC. 角平分线的性质的应用 如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.
求证:PM=PN.
证明:∵OD平分∠AOB,∠1=∠2,又∵OA=OB,OD=OD,∴△AOD≌△BOD,∴∠3=∠4,
又∵PM⊥DB,PN⊥DA,
∴PM=PN(角平分线上的点到角两边的距离相等). 如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A. PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PCD 如图,在△ABC中,∠B,∠C的平分线交于点O,OD⊥AB于点D,OE⊥AC于点E,则OD与OE的大小关系是( )
A. OD>OE B.OD=OE
C. OD
4提示:存在两条垂线段——直接 应用.利用角平分线的性质求线段的长度 如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.4提示:存在一条垂线段——构造应用.1.应用角平分线性质:存在角平分线涉及距离问题2.联系角平分线性质:面积周长条件利用角平分线的性质所得到的等量关系进行转化求解(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°B?2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .3E1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .60BF3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A. SSS
B. ASA
C. AAS
D.角平分线上的点到角两边的距离相等A4. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )A.6 B.5 C.4 D.3DBCEADF6810 1. 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.解:(1)DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2)在Rt△CDB和Rt△EDB中,DC=DE,DB=DB,
∴Rt△CDB≌Rt△EDB(HL),
∴BE=BC=8.
∴ AE=AB–BE=2.
∴△AED的周长=AE+ED+DA=2+6=8.CD2.如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F. 求证:CE=CF.证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
∴DE=DF.
在Rt△CDE和Rt△CDF中,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF. 如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.角平分线尺规作图属于基本作图,必须熟练掌握性质定理一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等辅助线
添加过角平分线上一点向两边作垂线段为证明线段相等提供了又一途径第二课时角的平分线的判定 我们知道,角的平分线上的点到角的两边的距离相等,反过来,到角的两边的距离相等的点是否在这个角的平分线上呢?3. 学会判断一个点是否在一个角的平分线上.1. 理解角平分线判定定理.2. 掌握角平分线判定定理内容的证明方法并应用其解题.回
顾旧知ODPP到OA的距离PDP到OB的距离PE.P是角平分线上的点几何语言描述:∵ OC平分∠AOB,且PD⊥OA, PE⊥OB.∴ PD= PE.ACB角的平分线上的点到角的两边的距离相等. 叙述角平分线的性质定理.不必再证全等E 角平分线的判定角的内部到角的两边距离相等的点在角的平分线上. 交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?角平分线的性质:角的平分线上的点到角的两边的距离相等.∵ OC平分∠AOB,且PD⊥OA, PE⊥OB
∴ PD= PE几何语言:猜想:思考:这个结论正确吗?已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE. 求证:点P在∠AOB的角平分线上.证明:作射线OP, ∴点P在∠AOB 角的平分线上. 在Rt△PDO和Rt△PEO 中,(全等三角形的对应角相等). OP=OP(公共边),PD= PE(已知 ), ∵PD⊥OA,PE⊥OB.∴∠PDO=∠PEO=90°,∴Rt△PDO≌Rt△PEO( HL).∴∠AOP=∠BOP猜想证明判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.应用所具备的条件:定理的作用:判断点是否在角平分线上.应用格式:∵ PD⊥OA,PE⊥OB,PD=PE.∴点P 在∠AOB的平分线上.例1 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?DCS解:作夹角的角平分线OC,截取OD=2.5cm , D即为所求.O方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.角平分线的判定的应用1.如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,PC=3 cm,当PD=____cm时点P在∠AOB的平分线上.332.如图,AB∥CD,点P到AB,BC,CD的距离相等,则点P是 的平分线与 的平分线的交点.∠ABC∠BCD 分别画出下列三角形三个内角的平分线,你发现了什么?三角形的内角平分线发现:三角形的三条角平分线相交于一点. 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?发现:过交点作三角形三边的垂线段相等.你能证明这个结论吗?已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.D E F 证明结论 点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?点P在∠A的平分线上. 结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.D E F EO 如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和.
12BCA解:连接OC.
如图,在直角△ABC中,∠C=900,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.1.应用角平分线性质:存在角平分线涉及距离问题2.联系角平分线性质:距离面积周长条件例2 如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )A.110° B.120° C.130° D.140°A解析:由已知,O到三角形三边的距离相等,即三条角
平分线的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∠ABC+∠ACB=180°-40°=140°,
∠OBC+∠OCB=70°,
∠BOC=180°-70°=110°.利用三角形的内角平分线的性质求值 方法点拨 由已知,O 到三角形三边的距离相等,得O是三角形三条内角平分线的交点,再利用三角形内角和定理即可求出∠BOC的度数.角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定 归纳总结3.到三角形三边距离相等的点是( )
A.三边垂直平分线的交点
B.三条高所在直线的交点
C.三条角平分线的交点
D.三条中线的交点
4.如图,河南岸有一个工厂在公路西侧,工厂到公路的距离与到河岸的距离相等,并且与B的距离为300 m,在图上标出工厂的位置,并说明理由.
解:作小河与公路夹角的角平分线BM,在BM上截取BP=1.5 cm,则点P即为所求的工厂的位置C证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
又∵∠BDE=∠CDF, BE=CF,
∴△BDE≌△CDF(AAS)
∴DE=DF,
∴AD平分∠BAC.
(2019?青岛模拟)如图,已知,BE=CF,BF⊥AC于点F,DE⊥AB于点E,BF,CE交于点D.
求证:AD平分∠BAC.1. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.小区CAOBMN2. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.P 如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.E证明:∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,∴点F在∠DAE的平分线上. GHMABCFD 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置. P1P2P3P4l1l2l3角平分线
的判定定理内容角的内部到角两边距离相等的点在这个角的平分线上作用判断一个点是否在角的平分线上结论三角形的角平分线相交于内部一点 1. 从课后习题中选取;
2. 完成练习册本课时的习题.课后作业
