13.1.2 线段的垂直平分线的性质课件(共两课时,58张PPT)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质课件(共两课时,58张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 00:00:00 | ||
图片预览






文档简介
课件58张PPT。13.1 轴对称
13.1.2 线段的垂直平分线的性质第一课时第二课时第一课时线段的垂直平分线的性质 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1ABL实际问题2 在成渝高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?成 渝 高 速 公 路3.会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.
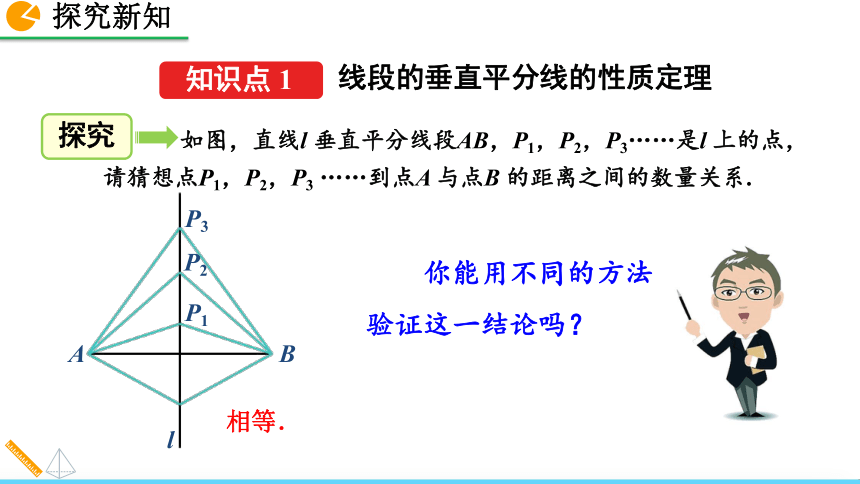
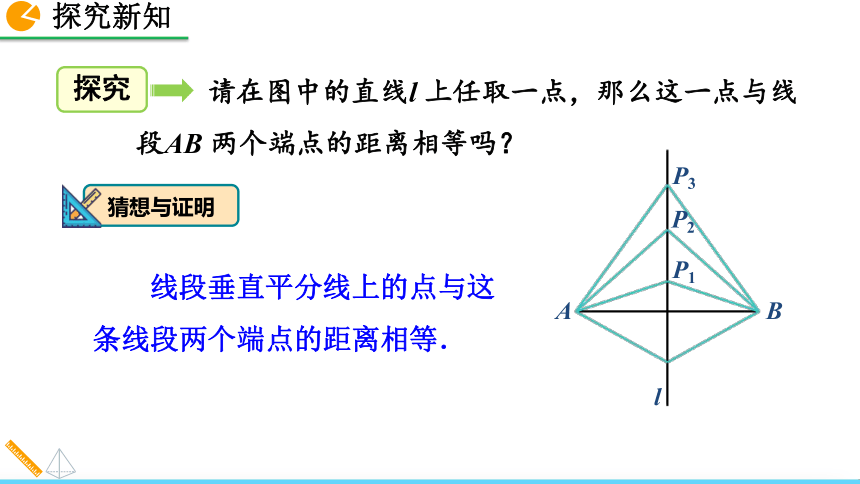
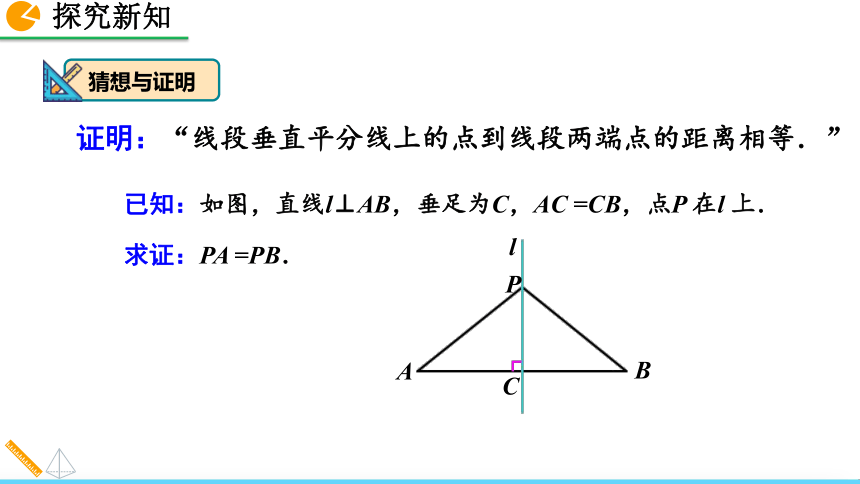
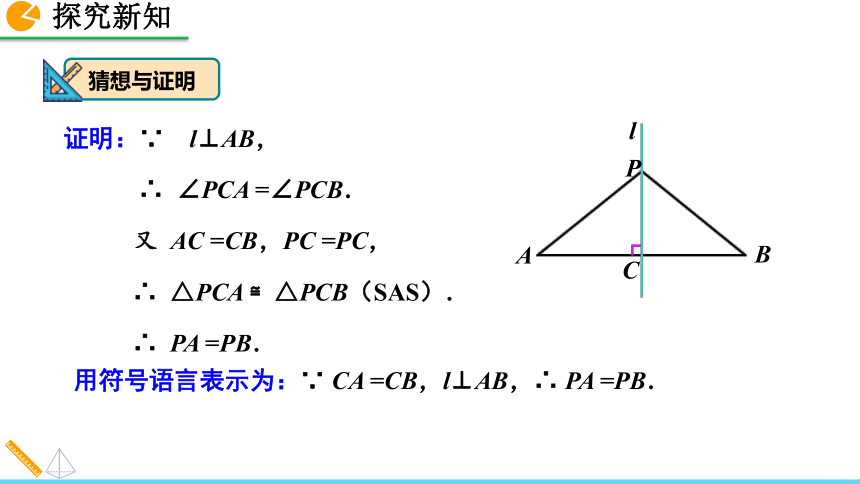
1. 理解线段垂直平分线的性质和判定.2. 能运用线段垂直平分线的性质和判定解决实际问题. 你能用不同的方法验证这一结论吗? 如图,直线l 垂直平分线段AB,P1,P2,P3……是l 上的点,请猜想点P1,P2,P3 ……到点A 与点B 的距离之间的数量关系.相等. 线段的垂直平分线的性质定理 请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条线段两个端点的距离相等.猜想与证明证明:“线段垂直平分线上的点到线段两端点的距离相等.”猜想与证明用符号语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB.证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.猜想与证明线段垂直平分线的性质:
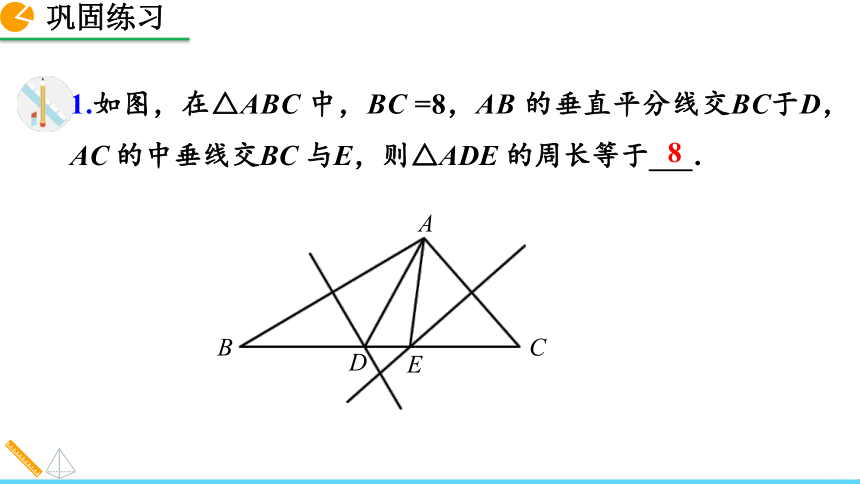
线段垂直平分线上的点到这条线段两个端点的距离相等.1.如图,在△ABC 中,BC =8,AB 的垂直平分线交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等于___.
8解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
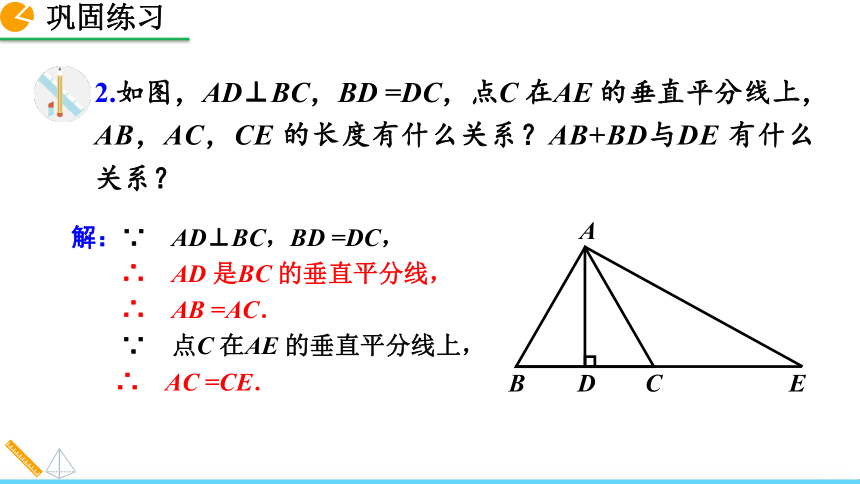
∴ AC =CE.2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?解: AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系? 反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.线段的垂直平分线的判定定理证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.猜想与证明 这些点能组成什么几何图形? 你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.l试一试例1 如图,已知:在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.证明:∵OB=OC,
∴点O在BC的垂直平分线上,
又AB=AC,
∴点A在BC的垂直平分线上,
即A,O均在BC的垂直平分线上,
∴AO⊥BC线段垂直平分线的判定定理的应用3.如图,已知在△ABC中,ON是AB的垂直平分线,并且OA=OC.
求证:点O在 BC的垂直平分线上.
∴点O在BC的垂直平分线上.(到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上)证明:连结OB.∵ ON是AB的垂直平分线(已知)∴ OA=OB(线段的垂直平分线上的点到这条线段的两个端点的距离相等)∵ OA=OC(已知) ∴ OB=OC(等量代换) 如何用尺规作图的方法经过直线外一点作已知直线的垂线?过直线外一点作已知直线的垂线(1)为什么任意取一点K ,使点K与点C 在直线两旁?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?4. 如图,求作点P,使PA=PB,且点P到∠MON两边的距离相等. 解:(1)作∠MON的角平分线;
(2)作线段AB的垂直平分线与∠MON的平分线交于点P,那么,点P即为所求作的点.解析:∵DE是AC的垂直平分线,∴DA=DC,∴∠DAC=∠C=25°,∵∠B=60°,∠C=25°,∴∠BAC=95°,∴∠BAD=∠BAC–∠DAC=70°.1.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°2.(2018?南充)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.B241.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm B.10 cm
C.15 cm D.17.5 cmC2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定CC3.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.7.84. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.AC解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.1. 如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在什么位置?答:△ABC 三边垂直平分线的交点上.2.如图,已知E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D.求证:OE垂直平分CD. 证明:E在∠AOB的平分线上,ED⊥OB于D.EC⊥OA于C,
∴ED=EC
在Rt△EDO和Rt△ECO中ED=EC,OE=OE
∴Rt△EDO≌Rt△ECO
∴OD=OC
∴O,E都在CD的垂直平分线上,
∴OE垂直平分CD. 如图,已知AB比AC长2 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm.
即AC+AB=14 cm.
设AB=x cm,AC=y cm.
根据题意,得 解得
∴AB长为8 cm,AC长为6 cm.线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等.判定与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.集合
定义线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.关系第二课时作线段的垂直平分线 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?AB公路3. 能够运用尺规作图的方法解决简单的作图问题.1. 能用尺规作已知线段的垂直平分线. 2. 进一步了解尺规作图的一般步骤和作图语言,理解作图的依据.线段垂直平分线的画法有时我们感觉一(两)个平面图形是轴对称的,如何验证呢? 通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称图形.不折叠图形,你能准确地作出轴对称图形的对称轴吗? 问题1:问题2: 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.作法:(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.(2)作直线CD. CD即为所求.特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点. 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?AB分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点即可.例1 如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.
(保留作图痕迹,不要求写出作法);
(2)在(1)所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.利用线段的垂直平分线的性质作图解:(1)如图所示:(2)在△AMP和△BNP中,∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),∴∠MAP=∠NPB.P1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D例2 如图,某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)利用作图解决实际问题方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在两点连线的垂直平分线上.两线的交点即为所求.解:如图所示:2.电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?在图上标出它的位置.解:如图所示,两条高速公路相交的角的角平分线和AB的垂直平分线的交点P1与P2点.作轴对称图形的对称轴下图中的五角星有几条对称轴?如何作出这些对称轴呢? AB作法:
(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.则l就是这个五角星的一条对称轴. l 用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴. 方法总结:对于轴对称图形,只要找到任意一组对称点,作出对称点所连线段的垂直平分线,即能得此图形的对称轴.例3 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.作轴对称图形的对称轴lPQ方法总结:
①过成轴对称图形的两组对应点的连线(或延长线)交点的直线是这个轴对称图形的对称轴.
②如果成轴对称的两个图形对称点连线(或延长线)相交,那么交点必定在对称轴上.3.作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?解析:∵DE垂直平分线段AC,∴DA=DC,AE=EC=6cm,
∵AB+AD+BD=13cm,∴AB+BD+DC=13cm,
∴△ABC的周长=AB+BD+BC+AC=13+6=19cm, (2018?襄阳)如图,在△ABC中,分别以点A和点C为圆心,大于
AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.19cm C.22cm D.25cmB1.(2018?河北)尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ
B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ
D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣ⅢD2.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
甲:分别作∠ACP、∠BCP的平分线,分别
交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB
于D、E,则D、E两点即为所求.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都错误
C.甲正确,乙错误 D.甲错误,乙正确 D3.如图,与图形A 成轴对称的是哪个图形?画出对称轴. 4.如图,角是轴对称图形吗?如果是,它的对称轴是什么? 角是轴对称图形,角平分线所在的直线就是角的对称轴. 如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.BC 学校在连接任意两点的两条线段的垂直平分线的交点处.A 如图,在4×3的正方形网格中,阴影部分是由4个正方形组成的一个图形,请你用两种方法分别在如图方格内填涂2个小正方形,使这6个小正方形组成的图形是轴对称图形,并画出其对称轴.线段的垂直
平分线的
有关作图尺规作图作对称轴的常见方法属于基本作图之一,必须熟熟练掌握.(1)将图形对折;
(2)用尺规作图;
(3)用刻度尺先取一对对称点连线的中点,然后作垂线.1 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
13.1.2 线段的垂直平分线的性质第一课时第二课时第一课时线段的垂直平分线的性质 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1ABL实际问题2 在成渝高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?成 渝 高 速 公 路3.会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.
1. 理解线段垂直平分线的性质和判定.2. 能运用线段垂直平分线的性质和判定解决实际问题. 你能用不同的方法验证这一结论吗? 如图,直线l 垂直平分线段AB,P1,P2,P3……是l 上的点,请猜想点P1,P2,P3 ……到点A 与点B 的距离之间的数量关系.相等. 线段的垂直平分线的性质定理 请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条线段两个端点的距离相等.猜想与证明证明:“线段垂直平分线上的点到线段两端点的距离相等.”猜想与证明用符号语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB.证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.猜想与证明线段垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.1.如图,在△ABC 中,BC =8,AB 的垂直平分线交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等于___.
8解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?解: AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系? 反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.线段的垂直平分线的判定定理证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.猜想与证明 这些点能组成什么几何图形? 你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.l试一试例1 如图,已知:在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.证明:∵OB=OC,
∴点O在BC的垂直平分线上,
又AB=AC,
∴点A在BC的垂直平分线上,
即A,O均在BC的垂直平分线上,
∴AO⊥BC线段垂直平分线的判定定理的应用3.如图,已知在△ABC中,ON是AB的垂直平分线,并且OA=OC.
求证:点O在 BC的垂直平分线上.
∴点O在BC的垂直平分线上.(到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上)证明:连结OB.∵ ON是AB的垂直平分线(已知)∴ OA=OB(线段的垂直平分线上的点到这条线段的两个端点的距离相等)∵ OA=OC(已知) ∴ OB=OC(等量代换) 如何用尺规作图的方法经过直线外一点作已知直线的垂线?过直线外一点作已知直线的垂线(1)为什么任意取一点K ,使点K与点C 在直线两旁?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?4. 如图,求作点P,使PA=PB,且点P到∠MON两边的距离相等. 解:(1)作∠MON的角平分线;
(2)作线段AB的垂直平分线与∠MON的平分线交于点P,那么,点P即为所求作的点.解析:∵DE是AC的垂直平分线,∴DA=DC,∴∠DAC=∠C=25°,∵∠B=60°,∠C=25°,∴∠BAC=95°,∴∠BAD=∠BAC–∠DAC=70°.1.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°2.(2018?南充)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.B241.如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于点D,若△DBC的周长为35 cm,则BC的长为( )
A.5 cm B.10 cm
C.15 cm D.17.5 cmC2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定CC3.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.7.84. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.AC解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.1. 如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在什么位置?答:△ABC 三边垂直平分线的交点上.2.如图,已知E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D.求证:OE垂直平分CD. 证明:E在∠AOB的平分线上,ED⊥OB于D.EC⊥OA于C,
∴ED=EC
在Rt△EDO和Rt△ECO中ED=EC,OE=OE
∴Rt△EDO≌Rt△ECO
∴OD=OC
∴O,E都在CD的垂直平分线上,
∴OE垂直平分CD. 如图,已知AB比AC长2 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm.
即AC+AB=14 cm.
设AB=x cm,AC=y cm.
根据题意,得 解得
∴AB长为8 cm,AC长为6 cm.线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等.判定与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.集合
定义线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.关系第二课时作线段的垂直平分线 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?AB公路3. 能够运用尺规作图的方法解决简单的作图问题.1. 能用尺规作已知线段的垂直平分线. 2. 进一步了解尺规作图的一般步骤和作图语言,理解作图的依据.线段垂直平分线的画法有时我们感觉一(两)个平面图形是轴对称的,如何验证呢? 通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称图形.不折叠图形,你能准确地作出轴对称图形的对称轴吗? 问题1:问题2: 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.作法:(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.(2)作直线CD. CD即为所求.特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点. 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?AB分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点即可.例1 如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.
(保留作图痕迹,不要求写出作法);
(2)在(1)所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.利用线段的垂直平分线的性质作图解:(1)如图所示:(2)在△AMP和△BNP中,∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),∴∠MAP=∠NPB.P1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D例2 如图,某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)利用作图解决实际问题方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在两点连线的垂直平分线上.两线的交点即为所求.解:如图所示:2.电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?在图上标出它的位置.解:如图所示,两条高速公路相交的角的角平分线和AB的垂直平分线的交点P1与P2点.作轴对称图形的对称轴下图中的五角星有几条对称轴?如何作出这些对称轴呢? AB作法:
(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.则l就是这个五角星的一条对称轴. l 用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴. 方法总结:对于轴对称图形,只要找到任意一组对称点,作出对称点所连线段的垂直平分线,即能得此图形的对称轴.例3 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.作轴对称图形的对称轴lPQ方法总结:
①过成轴对称图形的两组对应点的连线(或延长线)交点的直线是这个轴对称图形的对称轴.
②如果成轴对称的两个图形对称点连线(或延长线)相交,那么交点必定在对称轴上.3.作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?解析:∵DE垂直平分线段AC,∴DA=DC,AE=EC=6cm,
∵AB+AD+BD=13cm,∴AB+BD+DC=13cm,
∴△ABC的周长=AB+BD+BC+AC=13+6=19cm, (2018?襄阳)如图,在△ABC中,分别以点A和点C为圆心,大于
AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.19cm C.22cm D.25cmB1.(2018?河北)尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ
B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ
D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣ⅢD2.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
甲:分别作∠ACP、∠BCP的平分线,分别
交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB
于D、E,则D、E两点即为所求.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都错误
C.甲正确,乙错误 D.甲错误,乙正确 D3.如图,与图形A 成轴对称的是哪个图形?画出对称轴. 4.如图,角是轴对称图形吗?如果是,它的对称轴是什么? 角是轴对称图形,角平分线所在的直线就是角的对称轴. 如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.BC 学校在连接任意两点的两条线段的垂直平分线的交点处.A 如图,在4×3的正方形网格中,阴影部分是由4个正方形组成的一个图形,请你用两种方法分别在如图方格内填涂2个小正方形,使这6个小正方形组成的图形是轴对称图形,并画出其对称轴.线段的垂直
平分线的
有关作图尺规作图作对称轴的常见方法属于基本作图之一,必须熟熟练掌握.(1)将图形对折;
(2)用尺规作图;
(3)用刻度尺先取一对对称点连线的中点,然后作垂线.1 . 从课后习题中选取;
2 . 完成练习册本课时的习题。
